(04.02 MC)
The two-way frequency table contains data about how students access courses.
Traditional Online Row totals
Computer 28 62 90
Mobile device 46 64 110
Column totals 74 126 200
What is the joint relative frequency of students who use a mobile device in a traditional class?
23%
37%
46%
72%
Answers
The joint relative frequency of students using mobile devices in traditional classes, is
How to find the joint relative frequency ?The joint relative frequency of students that use mobile devices in the setting of a traditional class is :
= Number of students using mobile devices in traditional class / Number of total students accessing courses
Number of students using mobile devices in traditional class = 46 students
Number of total students accessing courses = 200
The joint relative frequency of students using mobile devices in traditional classes :
= 46 / 200
= 23 %
Find out more on joint relative frequency at https://brainly.com/question/29440032
#SPJ1
Related Questions
PLEASE HELP FAST!!! Estimate the line of best fit using two points on the line.

Answers
Answer:
D) y= -1/2x+9
Step-by-step explanation:
if u substitute y with 8 u will get 2
if u substitute y with 5 u will get 8
Answer:
D
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
Calculate m using the slope formula
m = \(\frac{y_{2}=xy_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (2, 8) and (x₂, y₂ ) = (8, 5)
m = \(\frac{5-8}{8-2}\) = \(\frac{-3}{6}\) = - \(\frac{1}{2}\)
The line crosses the y- axis at (0, 9) ⇒ c = 9
y = - \(\frac{1}{2}\) x + 9 → D
Hazel is saving her allowance to buy a new handbag to match her favorite dress. The handbag is shaped like a trapezoid with one base that is 23 centimeters long and another base that is 17 centimeters long. The trapezoid has an area of 260 square centimeters. What is the height of the trapezoid? Write your answer as a whole number or decimal. Do not round.
Answers
The height of the trapezoid is 13cm.
What is the height of the trapezoid?A trapezoid is a convex quadrilateral with at least one pair of parallel sides.
Area of a trapezoid = 0.5 x (sum of the lengths of the parallel sides) x height
Height = area / (0.5 x sum of lengths)
Sum of lengths = 23 + 17 = 40 cm
= 260 / (0.5 x 40) = 13 cm
To learn more about trapezoids, please check: https://brainly.com/question/25748893
#SPJ1
what is the probability that if 8 letters are typed, no letters are repeated? the probability that no letters are repeated is
Answers
The probability that no letters are repeated is 0.4121.
Divide the total number of outcomes by the entire number of different ways an event could happen to arrive at the probability. There are differences between probability and odds. The possibility of an event happening divided by the likelihood that it won't happen yields the odds. Probability is a metric used to assess the likelihood that a specific event will occur. The likelihood that the coin will land with the heads side up is measured using the probability concept when we toss it in the air. Here is an example of how probability is used in everyday life that you probably already know about. Prior to a major outing, we always consult the weather prediction.
So, the probability
Given, Number of letters=8
N\(=26*25*24*23*22*21*20*19\)
P\(=\frac{25}{26}*\frac{24}{26}*\frac{23}{26}*\frac{22}{26}*\frac{21}{26}*\frac{20}{26}\\=0.96*0.92*0.88*0.85*0.81*0.77\\=0.4121\)
Learn more about probability here
https://brainly.com/question/13604758
#SPJ4
Construct finite-state machines that act as recognizers for the input described by producing an output of 1 exactly when the input received to that point matches the description. (The input and output alphabet in each case is 0, 13.) (a) The set of all strings where the number of Os is a multiple of 3 (b) The set of all strings containing at least four 1s (c) The set of all strings containing exactly one 1 (d) The set of all strings beginning with 000 (e) The set of all strings where the second input is 0 and the fourth input is 1 (f) The set of all strings consisting entirely of any number (including none) of 01 pairs or consisting entirely of two Is followed by any number (including none) of Os (g) The set of all strings ending in 110 h) The set of all strings containing
Answers
Finite-state machines for given inputs: (a) 0s multiple of 3: 3-state machine. (b) At least four 1s: 4-state machine. (c) Exactly one 1: 2-state machine. (d) Begins with 000: 3-state machine. (e) Second is 0, fourth is 1: 4-state machine. (f) 01 pairs or 2 1s + 0s: 3-state machine. (g) Ends in 110: 3-state machine.
To construct finite-state machines that act as recognizers for the given inputs, we can follow these guidelines:
(a) For the set of all strings where the number of 0s is a multiple of 3, we can use a finite-state machine with three states. Start with the initial state, and transition to the next state whenever a 0 is encountered. After three transitions, go back to the initial state. If the machine ends in the accepting state, output 1.
(b) For the set of all strings containing at least four 1s, we can use a finite-state machine with four states. Start with the initial state, and transition to the next state whenever a 1 is encountered. If the machine enters the final state after four transitions, output 1.
(c) For the set of all strings containing exactly one 1, we can use a finite-state machine with two states. Start with the initial state and transition to the final state when the first 1 is encountered. Output 1 only if the final state is reached.
(d) For the set of all strings beginning with 000, we can use a finite-state machine with three states. Start with the initial state and transition to the next state whenever a 0 is encountered. If the machine reaches the final state after three transitions, output 1.
(e) For the set of all strings where the second input is 0 and the fourth input is 1, we can use a finite-state machine with four states. Start with the initial state and transition to the next state based on the inputs. Output 1 only if the machine reaches the final state.
(f) For the set of all strings consisting entirely of any number (including none) of 01 pairs or consisting entirely of two 1s followed by any number (including none) of 0s, we can use a finite-state machine with three states. Start with the initial state and transition based on the inputs. Output 1 only if the final state is reached.
(g) For the set of all strings ending in 110, we can use a finite-state machine with three states. Start with the initial state and transition based on the inputs. Output 1 only if the final state is reached.
Learn more about finite-state machines
https://brainly.com/question/32268314
#SPJ11
Finite-state machines (FSMs) can be constructed to act as recognizers for specific patterns in input strings. These are examples of how to construct FSMs as recognizers for different patterns in input strings. Each FSM is designed to produce an output of 1 when the input received matches the description provided.
Let's consider the given cases and construct FSMs for each one.
(a) The set of all strings where the number of Os is a multiple of 3:
To construct an FSM for this, we can keep track of the number of Os encountered so far. Initially, set the count to zero. When an O is encountered, increment the count by one. If the count becomes a multiple of 3, the FSM outputs 1; otherwise, it outputs 0. Reset the count to zero whenever a 1 is encountered.
(b) The set of all strings containing at least four 1s:
To create an FSM for this, we can keep track of the number of 1s encountered so far. Initially, set the count to zero. When a 1 is encountered, increment the count by one. If the count becomes equal to or greater than four, the FSM outputs 1; otherwise, it outputs 0.
(c) The set of all strings containing exactly one 1:
To build an FSM for this, we can have two states: a "no 1 encountered" state and a "1 encountered" state. Initially, start in the "no 1 encountered" state. Whenever a 1 is encountered, transition to the "1 encountered" state. If another 1 is encountered in the "1 encountered" state, transition to a third "more than one 1 encountered" state. In this case, the FSM outputs 0. Otherwise, if no additional 1s are encountered, the FSM outputs 1.
(d) The set of all strings beginning with 000:
To create an FSM for this, start in an initial state. When a 0 is encountered, transition to a second state. If two consecutive 0s are encountered in the second state, transition to a third state. Finally, if a third 0 is encountered in the third state, the FSM outputs 1; otherwise, it outputs 0.
(e) The set of all strings where the second input is 0 and the fourth input is 1:
To construct an FSM for this, start in an initial state. When the first input is read, transition to a second state. In the second state, transition to a third state if the second input is 0. In the third state, transition to a fourth state if the third input is not 0. Finally, in the fourth state, if the fourth input is 1, the FSM outputs 1; otherwise, it outputs 0.
(f) The set of all strings consisting entirely of any number (including none) of 01 pairs or consisting entirely of two Is followed by any number (including none) of Os:
To create an FSM for this, we can have multiple states to represent different scenarios. We start in an initial state and transition to a second state when a 0 is encountered. In the second state, transition back to the initial state if a 1 is encountered. If a 1 is encountered in the initial state, transition to a third state. In the third state, transition to a fourth state if an O is encountered. Finally, if an O is encountered in the fourth state, the FSM outputs 1; otherwise, it outputs 0.
(g) The set of all strings ending in 110:
To construct an FSM for this, start in an initial state. Transition to a second state if a 1 is encountered. In the second state, transition to a third state if a 1 is encountered again. Finally, if a 0 is encountered in the third state, the FSM outputs 1; otherwise, it outputs 0.
Learn more about Finite-state machines
https://brainly.com/question/32998825
#SPJ11
Use the drawing tool(s) to form the correct answers on the provided number line.
Yeast, a key ingredient in bread, thrives within the temperature range of 90°F to 95°FWrite and graph an inequality that represents the temperatures where yeast will NOT thrive.

Answers
The inequality of the temperatures where yeast will NOT thrive is T < 90°F or T > 95°F
Writing an inequality of the temperatures where yeast will NOT thrive.from the question, we have the following parameters that can be used in our computation:
Yeast thrives between 90°F to 95°F
For the temperatures where yeast will not thrive, we have the temperatures to be out of the given range
Using the above as a guide, we have the following:
T < 90°F or T > 95°F.
Where
T = Temperature
Hence, the inequality is T < 90°F or T > 95°F.
Read more about inequality at
https://brainly.com/question/32124899
#SPJ1
Let an = 5n/4n + 1 Determine whether {an) is convergent. convergent divergent
Answers
To determine whether the sequence {an} = 5n/4n + 1 is convergent or divergent, we can analyze its behavior as n approaches infinity.
First, let's rewrite the expression for the nth term of the sequence:
an = 5n / (4n + 1)
As n approaches infinity, the denominator 4n + 1 becomes dominant compared to the numerator 5n. Therefore, we can simplify the expression by neglecting the term 5n:
an ≈ n / (4n + 1)
Now, we can consider the limit of the sequence as n approaches infinity:
lim(n→∞) n / (4n + 1)
To evaluate this limit, we can divide both the numerator and denominator by n:
lim(n→∞) (1 / 4 + 1/n)
As n approaches infinity, the term 1/n approaches zero, leaving us with:
lim(n→∞) 1 / 4 = 1/4
Since the limit of the sequence is a finite value (1/4), we can conclude that the sequence {an} = 5n/4n + 1 is convergent.
In other words, as n gets larger and larger, the terms of the sequence {an} get closer and closer to the limit of 1/4. This indicates that the sequence approaches a fixed value and does not exhibit wild oscillations or diverge to infinity. Therefore, we can say that the sequence is convergent.
To learn more about convergent click here:
brainly.com/question/31756849
#SPJ11
Forty observations were used to estimate y = β0 + β1x1 + β2x2 + ε. The regression results is shown in the accompanying table.Coefficients Standard Error t Stat p-ValueIntercept 13.83 2.42 5.71 1.56E-06x1 −2.53 0.15 −16.87 5.84E-19x2 0.29 0.06 4.83 2.38E-05a. Interpret the point estimate for β1.As x1 increases by 1 unit, y is predicted to decrease by 2.53 units.As x1 increases by 1 unit, y is predicted to increase by 0.29 units.As x1 increases by 1 unit, y is predicted to decrease by 2.53 units, holding x2 as a constant.As x1 increases by 1 unit, y is predicted to increase by 0.29 units, holding x2 as a constant.b. What is the sample regression equation? (Round your answers to 2 decimal places.); could you please explain this part!!!!!!!formula794.mml _____ − ______x1 + ______x2.c. What is the predicted value for y if x1 = −9 and x2 = 25. (Round your answer to 2 decimal places.)formula795.mml
Answers
a. As per the regression results table, the point estimate for β1 is -2.53. Therefore, as x1 increases by 1 unit, y is predicted to decrease by 2.53 units, holding x2 as a constant.
b. The sample regression equation can be written as:
y = 13.83 - 2.53x1 + 0.29x2
c. To find the predicted value for y if x1 = -9 and x2 = 25, we can substitute these values in the sample regression equation:
y = 13.83 - 2.53(-9) + 0.29(25)
y = 13.83 + 22.77 + 7.25
y = 43.85
Therefore, the predicted value for y is 43.85 when x1 = -9 and x2 = 25.
a. The correct interpretation for the point estimate of β1 is: As x1 increases by 1 unit, y is predicted to decrease by 2.53 units, holding x2 as a constant.
b. The sample regression equation can be found using the coefficients given in the table. The equation is: y = 13.83 - 2.53x1 + 0.29x2 (rounded to 2 decimal places).
c. To find the predicted value of y when x1 = -9 and x2 = 25, plug these values into the regression equation: y = 13.83 - 2.53(-9) + 0.29(25). After calculating, the predicted value for y is 45.84 (rounded to 2 decimal places).
Visit here to learn more about regression equation : https://brainly.com/question/30738733
#SPJ11
The regular price of a burger meal at a certain restaurant is $8.70. It is on sale for a 20% discount. What is the sale price of the hamburger meal?
Answers
Answer:
1.74
Step-by-step explanation:
Find the regression equation, letting the first variable be the predictor (x) variable. Find the best predicted Nobel Laureate rate for a country that has 78.2 Internet users per 100 people. How does it compare to the country's actual Nobel Laureate rate of 1.6 per 10 million people? LOADING... Click the icon to view the data. Find the equation of the regression line. y=nothing+(nothing)x (Round the constant to one decimal place as needed. Round the coefficient to three decimal places as needed.) The best predicted number of Nobel Laureates when the number of internet users per 100 is 78.2 is nothing. (Round to one decimal place as needed.)How does it compare to the country's actual Nobel Laureate rate of 1.6 per 10 million people? A. The best predicted value is very close to the actual Nobel Rate. B. The best predicted value is not at all close to the actual Nobel Rate. C. The best predicted value is the opposite of the actual Nobel Rate. D. The best predicted value is equal to the actual Nobel Rate.
Answers
Answer: the answe is not at all close to the actual Nobel rate.
Step-by-step explanation:
How many right angle are there in l?
Answers
There is one right angle in the L angle.
A right angle is one that is 90 degrees in length. It is the most frequently encountered angle in our daily lives. It can be noticed in room corners, box edges, mobile phone screens, and so on.
A square's and a rectangle's sides always make a right angle with each other. It is represented in radians as /2.
The angle formed by two lines that are perpendicular to each other is called a right angle. A right angle is equal to 90° and is in the shape of the letter "L". In the following figure, ray AB and BC form a right angle ABC.
Thus, there is one right angle in the L angle.
Complete question: How many right angles are there in L angles?
To know more about L angle visit: brainly.com/question/18913751
#SPJ4
x+y=3
2x-y=0
substituition method
Answers
Answer:
(1, 2 )
Step-by-step explanation:
x + y = 3 (subtract x from both sides )
y = 3 - x → (1)
2x - y = 0 → (2)
Substitute y = 3 - x into (2)
2x - (3 - x) = 0
2x - 3 + x = 0
3x - 3 = 0 ( add 3 to both sides )
3x = 3 ( divide both sides by 3 )
x = 1
Substitute x = 1 into (1)
y = 3 - 1 = 2
solution is (1, 2 )
what is the slop of the line represented by y= 5x - 7
Answers
Answer:
The slope is
m =5
The y-intercept is
b =-7 or (0,7)
Step-by-step explanation:
Bryant Industries uses forecasting to estimate the number of orders that will be placed by their customers. The table below gives the sales figures for the last four months. Month 2 3 4 5 Sales 924 91
Answers
Bryant Industries uses forecasting to estimate the number of orders that will be placed by their customers. The table below gives the sales figures for the last four months.Month2345Sales92491942004There are different forecasting techniques used by companies like Bryant Industries to predict future sales.
One of the most widely used methods is the time-series method. This method is particularly useful when the demand for a product or service changes over time and when there are no external factors that affect the sales. In this case, we can use a time-series method called the moving average to estimate future sales. The moving average is a time-series method that uses the average of past sales data to estimate future sales. It is particularly useful when there are no external factors that affect the sales. In this case, we can use a 3-month moving average to estimate future sales. The 3-month moving average is calculated as follows: (924 + 919 + 420) / 3 = 754.33. This means that we can expect sales of around 754 units next month. The moving average method is easy to use and is a good way to get a quick estimate of future sales. However, it has some limitations. For example, it does not take into account external factors that may affect sales, such as changes in the economy or in consumer behavior.
In conclusion, Bryant Industries can use the moving average method to estimate future sales. However, they should also consider other factors that may affect sales, such as changes in the economy or in consumer behavior. By doing so, they can make more accurate forecasts and improve their overall performance.
To learn more about time-series method visit:
brainly.com/question/32443421
#SPJ11
what's the answer step by step please

Answers
The outer bottom edge of a staircase is in the shape of a helix of radius 1 meter. The staircase has a height of 4 meters and makes two complete revolutions from top to bottom. Find a vector-valued function for the staircase. Use a computer algebra system to graph your function. (There are many correct answers. Use t as the parameter. Let 0 t4.T.)
Answers
We can think of the staircase as a curve that spirals down around the outside of a cylinder with radius 1 and height 4. As we spiral down, we also move horizontally around the cylinder, making two complete revolutions.
To construct a vector-valued function for the staircase, we can start by parameterizing the cylinder. Let's use cylindrical coordinates, with height h, angle theta, and radius r. Then the cylindrical coordinates of a point on the cylinder are given by (h, theta, r), and we can convert to Cartesian coordinates using the formulas:
x = r cos(theta)
y = r sin(theta)
z = h
To make the staircase spiral down around the outside of the cylinder, we can use a third parameter, t, that controls the height of the staircase. We want the height to increase from 0 to 4 over the course of two revolutions, so we can use:
h = 2t
To make the staircase wrap around the outside of the cylinder, we can use the angle theta as a function of t. We want two complete revolutions, which corresponds to an angle of 4 pi. So we can use:
theta = 4 pi t
Finally, we need to determine the radius r as a function of t, so that the staircase follows a helical path around the cylinder. We want the radius to increase smoothly from 0 at the bottom of the staircase to 1 at the top, over the course of two revolutions. One way to do this is to use a function of the form:
r = a + b sin(2 pi t)
where a and b are constants that we can choose to get the desired behavior. To make the radius increase smoothly from 0 to 1, we can choose a = 0.5 and b = 0.5. This gives us:
r = 0.5 + 0.5 sin(2 pi t)
Putting it all together, we get the following vector-valued function for the staircase:
r(t) = (0.5 + 0.5 sin(2 pi t)) cos(4 pi t), (0.5 + 0.5 sin(2 pi t)) sin(4 pi t), 2t)
Visit here to learn more about cylinder brainly.com/question/16134180
#SPJ11
There are 5 1/2 pounds of bricks in a bag. Each brick weighs 2 3/4 pounds. How many bricks are in the bag?
Answers
Answer:
there are 2 bricks.
Step-by-step explanation:
2. The slope is the ______
3. A linear function can be represented by _____, where _____ are constants
4. A linear function has _____. a zero, or_____ unless it is a _____
5. The domain is the set of values for which ______
6. The ______ represents the average of a set of numbers
7. A constant function has a slope _____
Answers
2. The slope is the measure of how steep a line is.
3. A linear function can be represented by equation y = mx + b, where slope (m) and y-intercept (b) are constants are constants.
4. A linear function has constant slope. a zero, or horizontal line unless it is a vertical line.
5. The domain is the set of values for which function is defined.
6. The Mean represents the average of a set of numbers
7. A constant function has a slope zero.
Given are the statements with blanks we need to fill them,
2) The slope is the measure of how steep a line is. It represents the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line.
3) A linear function can be represented by the equation y = mx + b, where y is the dependent variable, x is the independent variable, m is the slope, and b is the y-intercept. The slope (m) and y-intercept (b) are constants.
4) A linear function has a constant slope. It remains the same for every point on the line unless it is a horizontal line (where the slope is zero) or a vertical line (where the slope is undefined).
5) The domain is the set of values for which a function is defined or meaningful. In the case of a linear function, the domain is typically all real numbers unless there are restrictions or specific conditions mentioned.
6) The mean represents the average of a set of numbers. It is calculated by summing up all the values in the set and dividing the sum by the total number of values.
7) A constant function has a slope of zero. This means that the function remains flat and parallel to the x-axis, indicating that there is no change in the dependent variable as the independent variable varies.
Learn more about Algebra click;
https://brainly.com/question/953809
#SPJ4
If I took any two distinct prime numbers, and the number "1", would these numbers always be pairwise relatively prime? True O False
Answers
The statement is true. If we take any two distinct prime numbers, and the number "1", these numbers will always be pairwise relatively prime.
Two numbers are said to be pairwise relatively prime if their greatest common divisor (GCD) is equal to 1. In this case, since we are considering distinct prime numbers, their GCD will always be 1 since prime numbers have no common factors other than 1 and themselves. Therefore, any two distinct prime numbers will be relatively prime.
Similarly, when we consider the number "1", it is relatively prime to any other number because its only divisor is 1. Hence, when "1" is paired with any prime number, the GCD will be 1.
In summary, whether we consider two distinct prime numbers or pair them with the number "1", the resulting numbers will always be pairwise relatively prime.
Learn more about prime numbers here: https://brainly.com/question/29629042
#SPJ11
Anybody know the answer?

Answers
Answer: 10 days
Step-by-step explanation: It should be 10 days, I checked just to make sure. Here's the original reply I put before:
It's a fifth of the workers compared to before (2 now compared to 10 before). If 10 workers need 5 days, then 2 workers need 5 times that, so around 25 days, however that's considering they do 2 hours a day. The problem is that they do 5 hours now, so its 2.5 times more, so ideally they would take less time, meaning you divide 25 by 2.5, which gives 10 days.
Please I need help Graph the following polynomials finding all key features including x-intercepts, y-intercept, máximums, end behavior, and multiplicity

Answers
Given:
There are given the polynomial equation:
\(f(x)=(x-2)(x+2)^3(x+6)\)Now,
We need to find the value for the x-intercept, y-intercept, maximum, end behaviors, and multiplicity.
So,
First, find the x-intercept and y-intercept:
To find the x-intercept put 0 for y and to find the y-intercept 0 for x.
Then,
The x-intercept and y-intercept are shown below:
\(\begin{gathered} f(x)=(x-2)(x+2)^{3}(x+6) \\ x-intercept:(2,0),(-2,0),(-6,0) \\ y-intercept:(0,-96) \end{gathered}\)Now,
The value of maximum and minimum, end behavior and multiplicity is shown below:
\(\begin{gathered} End\text{ behaviour: falls to the left and rise to the right} \\ Multiplicity:1,3,1 \end{gathered}\)Final answer:
Hence, the value of x-intercept, y-intercept, end behaviour and multiplicity are shown below:
\(\begin{gathered} x-\imaginaryI ntercept:(2,0),(-2,0),(-6,0) \\ y-intercept:(0,-96) \\ End\text{behav}\imaginaryI\text{our: falls to the left and rise to the right} \\ Mult\imaginaryI pl\imaginaryI c\imaginaryI ty:1,3,1 \end{gathered}\)on january 1, year 1, billy co signed a three-year lease for office space. the lease required monthly rent of $8,000 for the first year, $8,100 fo rhte second year
Answers
If on january 1, year 1, billy co signed a three-year lease for office space The amortization expense on this leasehold improvement that Billy should record for Year 2 is: $1,000.
How to find the amortization expense?Since we were told that the new overhead lighting fixtures is the amount of $2,000 now let determine the Amortization expense using this formula
Amortization expense = New overhead lighting fixtures / 2 years
Let plug in the formula
Amortization expense = $2,000 /2
Amortization expense = $1,000
Therefore the Amortization expense is the amount of $1,000.
Learn more about Amortization expense here:https://brainly.com/question/25530648
#SPJ1
The complete question:
On January 1 , Year 1, Billy Co. signed a three year lease for office space. The lease required monthly rent of 8,000 for the first year. 8,100 for the second year and 8,200 for the 3rd year. Billy has the option to renew the lease for a fourth year at 8,300 per month. On January 1, Year 2, Billy permanently installed new overhead lighting fixtures at a cost of $2,000. How much amortization expense on this leasehold improvement should Billy record for Year 2?
American jurists ____ and ____ defined law in a functional sense as predictions of the way that a court will decide specific legal questions.
Answers
American jurists (fill in the names) defined law as predictions of how a court will decide specific legal questions, based on a functional perspective.
American jurists Oliver Wendell Holmes Jr. and Benjamin Cardozo are known for their functionalist approach to defining law. They viewed law not merely as a set of abstract principles or rules, but as a prediction of how courts will decide specific legal questions in practice. According to their perspective, the law should be seen as a dynamic and evolving system that adapts to societal changes and reflects the judgments and decisions of the judiciary. By emphasizing the functional aspect of law, Holmes and Cardozo recognized the importance of considering how legal principles are actually applied and interpreted in real-world scenarios. Their approach acknowledges that the interpretation and application of law by judges can vary and evolve over time, depending on factors such as legal precedent, social context, and the specific facts of the cases before them.
Learn more about functionalist here:
https://brainly.com/question/31119150
#SPJ11
4
3
2
1
i
1
Which of the following is the correct equation in slope intercept form?*
(50 Points)
32
y3x+2
y-3/2x+3
y2/3x3

Answers
Part 2
5. -0.3 ÷ (-0.27)
6. -5.5 ÷ 0.021
7. -412 ÷ -334
8. 7.75 ÷ ( -123)
Answers
Answer:
5. -10/9
6. -5500/21
7. 1 39/167
8. -31/492
Maggie's brother is 5 years younger than three times her age. The sum of their ages is 23.
How old is Maggie?
Answers
Answer:8
Step-by-step explanation: 5 x 3= 15
23-15=8
Answer:
8
Step-by-step explanation:
5 times 3 =15 23 minus 15 is three
question 9
9. Given ABCD
EFGH, find the length of GH.
A. 8
B. 7
C. 5
D. 10
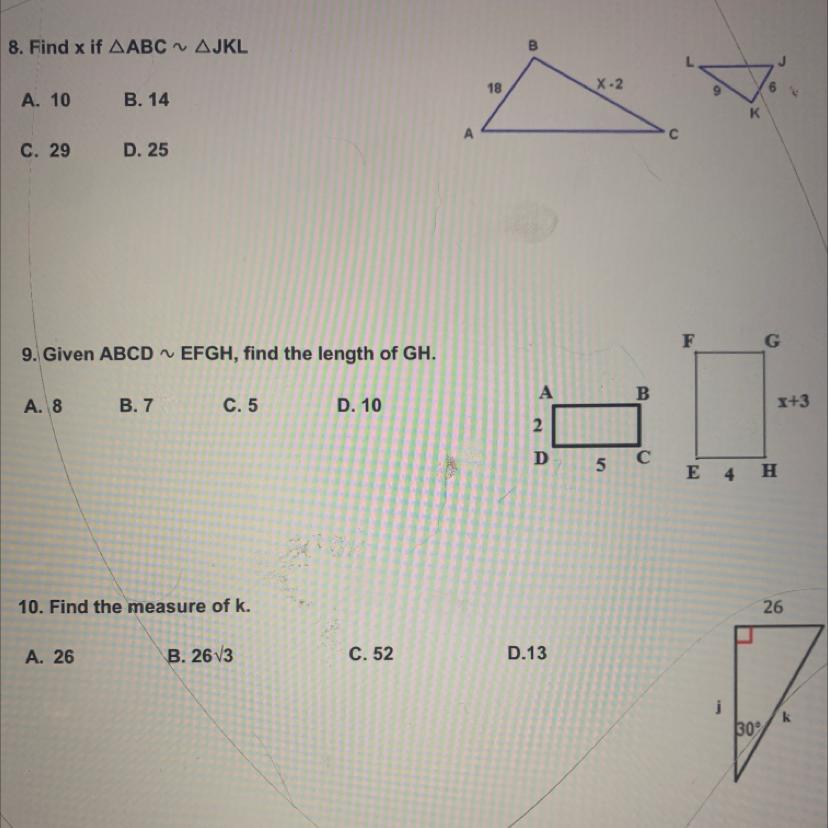
Answers
The step-step explanation:
Xander was in the lead for 75% of the laps during PE. If the race lasted 12 laps, how many laps did Xander lead?
Answers
Answer:
9 laps
Step-by-step explanation:
75% of something is the same as three-fourths, or multiplying by 0.75
12 x 0.75 = 9
or you can divide by 4 and then multiply by three if you know what to separate the original number into
12/4 = 3 3 x 3 = 9
Kennedy is making bracelets to give to her friends. she wants to put 20 beads on each bracelet. beads are sold in packages of 25. what is the least number of packages she can buy to make necklaces and have no beads?
Answers
Answer:11
Step-by-step explanation:
Answer:
4
Step-by-step explanation:
25+25+25+25=100
1. 2. 3. 4
Nendell saw the following sign at
a diner. If he bought one of each item
and spent $7.50, how much did the
drink cost?
Answers
Answer:
The drink cost $1.47
Step-by-step explanation:
GEOMETRY HONORS
Answer Options:
Valid: Law of Detachment
Valid: Law of Syllogism
No Valid Conclusions
All questions(17-21) must be answered, thank you all so muchhh

Answers
16. Valid
Reason: congruency can be represented by the symbol ≅ hence the statement still reads <1 and <2 are congruent.
17. Invalid
Reason: A rectangle also has four right angles, It is only a square when all the sides are equal.
18. Valid
Reason: congruency can be represented by the symbol ≅ hence the statement still reads <JKM and <MKL are congruent.
19. Valid
Reason: The conclusion of the battery dying is in support of the premise giving which is leaving the light on when the car is off.
20.Valid
Reason: The conclusion, Dante obtained a part time job is in line with the premise that obtaining a pert time job, is a way to afford a car payment
21. Valid
Reason: The premise which has that selling 75% of the prom tickets will make the prom hold at country club is fulfilled, hence the prom will be held at the country club
What are valid arguments?An argument is vailed when the premises or conditions of the argument are all true. when some part of the argument is not true then it will lead to invalid conclusion.
Read more on valid arguments here:
#SPJ1