Answers
2(3x^2-2x) + 2(x^2+7x-9)
= 6x^2 - 4x + 2x^2 +14x - 18
Simplify
8x^2 + 10x - 18
It would be number 4
Answer:
4.
Step-by-step explanation:
(x^2 + 7x - 9) + (3x^2 - 2x) + (x^2 + 7x - 9) + (3x^2 - 2x)
x^2 + 7x - 9 + 3x^2 - 2x + x^2 + 7x - 9 + 3x^2 - 2x
Rearranging order:
3x^2 + 3x^2 + x^2 + x^2 + 7x + 7x - 2x - 2x - 9 - 9
Combine like terms
8x^2 + 10x - 18
Related Questions
Please answer all these question



Answers
Answer:
it's 10.00 because I used a calculator
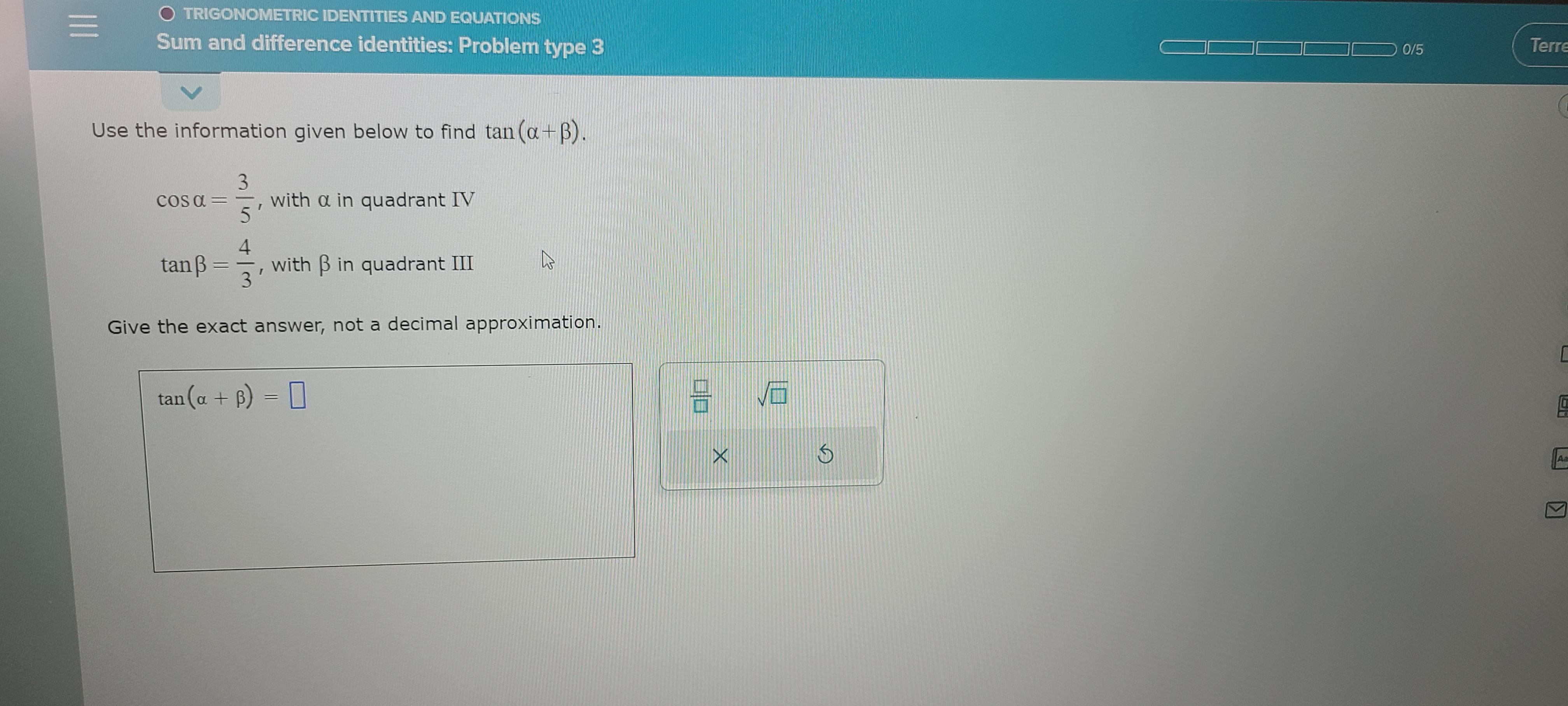
Use the information given below to find tan(a + B)
cos a = 3/5, with a in quadrant IV
tan B = 4/3, with B in quadrant I I I
Give the exact answer, not a decimal approximation.
tan(a + B) = ?
Answers
let's bear in mind that on the III Quadrant, sine and cosine are both negative, whilst on the IV Quadrant, sine is negative and cosine is positive, that said
\(\cos(\alpha )=\cfrac{\stackrel{adjacent}{3}}{\underset{hypotenuse}{5}}\hspace{5em}\textit{let's find the \underline{opposite side}} \\\\\\ \begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies o=\sqrt{c^2 - a^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{5}\\ a=\stackrel{adjacent}{3}\\ o=opposite \end{cases} \\\\\\ o=\pm \sqrt{ 5^2 - 3^2} \implies o=\pm \sqrt{ 16 }\implies o=\pm 4\implies \stackrel{IV~Quadrant }{o=-4} \\\\[-0.35em] ~\dotfill\)
\(\tan(\beta )=\cfrac{\stackrel{opposite}{4}}{\underset{adjacent}{3}}\implies \tan(\beta )=\cfrac{\stackrel{opposite}{-4}}{\underset{adjacent}{-3}} \\\\[-0.35em] ~\dotfill\\\\ \tan(\alpha + \beta) = \cfrac{\tan(\alpha)+ \tan(\beta)}{1- \tan(\alpha)\tan(\beta)} \\\\\\ \tan(\alpha + \beta)\implies \cfrac{ ~~\frac{-4}{3}~~ + ~~\frac{-4}{-3} ~~ }{1-\left( \frac{-4}{3} \right)\left( \frac{-4}{-3} \right)}\implies \cfrac{0}{1-\left( \frac{-4}{3} \right)\left( \frac{-4}{-3} \right)}\implies \text{\LARGE 0}\)
The triangle formed by a 4-foot-tall mail box and its 6-foot shadow is similar to the triangle formed by a utility pole and its 15-foot shadow at the same time of day. What scale factor is used to transform the image of the utility pole triangle from the preimage of the mailbox triangle? Use this scale factor to determine the height of the utility pole.
Answers
Answer:
The transformations used were rotations, reflections, and R(–3, –3). After a dilation, the image of P is. P'(4, 12). What is the scale factor of the dilation? 5.The triangle formed by a 4-foot-tall mail box and its 6-foot shadow is similar to the triangle formed by a utility pole and its 15-foot shadow at the same time of day.
Step-by-step explanation:
Use the number line to find the equivalent decimal and mixed number for givenletter

Answers
The equivalent decimal and mixed number for given letter C is,
⇒ C = 8.2 ; 8 2/10
We have to given that,
A number line is shown in image.
Since,
A number lines are the horizontal straight lines in which the integers are placed in equal intervals.
And, All the numbers in a sequence can be represented in a number line. This line extends indefinitely at both ends.
Now, By given number line,
Point C is two point left from point 8.
Hence, The point C is denoted as,
⇒ C = 8.2
⇒ C = 82/10
⇒ C = 8 2/10
Therefore, the equivalent decimal and mixed number for given letter C is,
⇒ C = 8.2 ; 8 2/10
Learn more about the coordinate visit:
https://brainly.com/question/24394007
#SPJ1
I need help as soon as possible! Please help me! Thank you very much! No links.
Answers
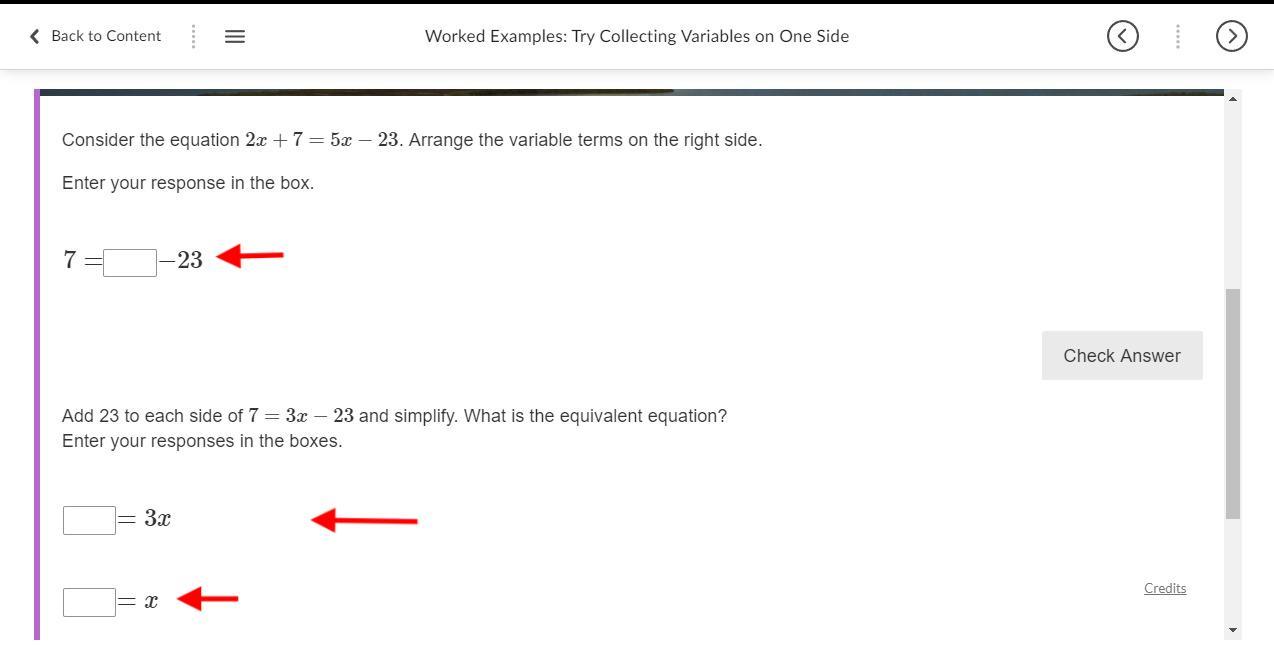
I need help I know the answer I just need someone to explain how they found the answer is x= 10, please help!
2x+7=5x-23
Answers
Answer and Step-by-step explanation: the doc is below for how i did the problem
Answer: x = 10
Step-by-step explanation:
To solve, we will isolate the variable x.
Given:
2x + 7 = 5x - 23
Add 23 to both sides of the equation:
2x + 30 = 5x
Subtract 2x from both sides of the equation:
30 = 3x
Divide both sides of the equation by 3:
10 = x
Reflexive property:
x = 10
Describe the graph that would be used to solve the equation -x^2+4=x+2 using a system of equations. How will you use the graph to find the solution(s)?
Answers
The solution of the equation -x² + 4 = x + 2 is at x = -2 and x = 1
What is an equation?An equation is an expression that shows how numbers and variables are related to each other.
Given the quadratic equation:
-x² + 4 = x + 2
Collecting like terms:
x² + x - 2 = 0
Plotting using a graph; the solution of the equation can be gotten by getting the point the graph crosses the x axis.
The solution is at x = -2 and x = 1
Find out more on equation at: https://brainly.com/question/25638875
#SPJ1

Is this statement true or false? The expression 4x (x2 + 4x + 3) is a polynomial. O True O False
Answers
Answer:
Step-by-step explanation:
If you remove the brackets you get
4x^2*x^2 + 4x*4x + 3*4x
4x^4 + 16x^2 + 12x
That definitely is a polynomial
In its factored form, one of the factors is a polynomial so the answer is true.
56/25 gal $41.05/20 gal
Answers
Answer:
56/25
Step-by-step explanation:
sksksjskskksdidid
The sale price of a new refrigerator is $648 and sales tax is figured at 0.10 times the price. What is the total amount paid for the refrigerator?
Answers
Answer:
$712.80
Step-by-step explanation:
648×0.10=64.8
648+64.8=712.8
The total amount paid for the refrigerator is $712.8.
What is an expression?An expression is a way of writing a statement with more than two variables or numbers with operations such as addition, subtraction, multiplication, and division.
Example: 2 + 3x + 4y = 7 is an expression.
We have,
Sale price = $648
Sales tax = 0.10 times the price
The total amount paid.
= 648 + 0.10 x 648
= 648 + 64.8
= 712.8
Thus,
The total amount paid is $712.8.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ2
Consider the function below, which has a relative minimum located at (-3, -18) and a relative maximum located at 1/3, 14/27). f(x) = -x3 - 4x2 + 3x. Select all ordered pairs in the table which are located where the graph of f(x) is decreasing: Ordered pairs: (-1, -6), (2, -18), (0, 0),(1 , -2), (-3 , -18), (-4. , -12)
Answers
The ordered pairs (-1, -6), (2, -18), (0, 0), and (-4, -12) do not correspond to the intervals where the graph of f(x) is decreasing. The pairs (1, -2) and (-3, -18) are the correct ones.
To determine where the graph of f(x) is decreasing, we need to examine the intervals where the function's derivative is negative. The derivative of f(x) is given by f'(x) = -3x^2 - 8x + 3.
Now, let's evaluate f'(x) for each of the given x-values:
f'(-1) = -3(-1)^2 - 8(-1) + 3 = -3 + 8 + 3 = 8
f'(2) = -3(2)^2 - 8(2) + 3 = -12 - 16 + 3 = -25
f'(0) = -3(0)^2 - 8(0) + 3 = 3
f'(1) = -3(1)^2 - 8(1) + 3 = -3 - 8 + 3 = -8
f'(-3) = -3(-3)^2 - 8(-3) + 3 = -27 + 24 + 3 = 0
f'(-4) = -3(-4)^2 - 8(-4) + 3 = -48 + 32 + 3 = -13
From the values above, we can determine the intervals where f(x) is decreasing:
f(x) is decreasing for x in the interval (-∞, -3).
f(x) is decreasing for x in the interval (1, 2).
Now let's check the ordered pairs in the table:
(-1, -6): Not in a decreasing interval.
(2, -18): Not in a decreasing interval.
(0, 0): Not in a decreasing interval.
(1, -2): In a decreasing interval.
(-3, -18): In a decreasing interval.
(-4, -12): Not in a decreasing interval.
Therefore, the ordered pairs (-1, -6), (2, -18), (0, 0), and (-4, -12) are not located in the intervals where the graph of f(x) is decreasing. The correct answer is: (1, -2), (-3, -18).
For more question on intervals visit:
https://brainly.com/question/30460486
#SPJ8
Note the complete and the correct question is
Q- Consider the function below, which has a relative minimum located at (-3, -18) and a relative maximum located at 1/3, 14/27).
\(f(x) = -x^3 - 4x^2 + 3x\).
Select all ordered pairs in the table which are located where the graph of f(x) is decreasing: Ordered pairs: (-1, -6), (2, -18), (0, 0),(1 , -2), (-3 , -18), (-4. , -12)
Consider the equation below.
Determine which equation has the same solutions as the given equation.

Answers
Answer:
B, (x-5) square =21
Step-by-step explanation:
B, (x-5)square =21
Find the 19th term in the geometric sequence, the first term being a=4 and the common ratio being r=2
Answers
The 19th term of a geometric sequence is 1048576.
What is a geometric sequence?A geometric sequence is a sequence of numbers in which the ratio between consecutive terms is constant.
We have,
a = 4 and r = 2
The nth term of a geometric sequence.
= a\(r^{n-1}\)
Now,
The 19th term of a geometric sequence.
= a\(r^{n-1}\)
Substituting a and r values.
= 4 x \(2^{19 - 1}\)
= 4 x \(2^{18}\)
= 4 x 262144
= 1048576
Thus,
The 19th term of a geometric sequence is 1048576.
Learn more about geometric sequence here:
https://brainly.com/question/2321576
#SPJ9
what are the features of the function g if g(x)= f(x+4) +8
Answers
The domain, range, x-intercept, or y-intercept of g(x) = f(x + 4) + 8. The features of g depend on the corresponding features of f.
Given the function g(x) = f(x + 4) + 8, let's examine its features:
Domain:
The domain of the function g will be the same as the domain of the function f, which depends on the restrictions or constraints of f. However, it is important to note that shifting the input by 4 units (x + 4) does not inherently change the domain unless there are specific restrictions imposed by f.
Range:
Similar to the domain, the range of the function g will depend on the range of the function f.
x-intercept:
The x-intercept of a function is the point where the graph intersects the x-axis, meaning the y-coordinate is zero (y = 0). To find the x-intercept of g(x), we set g(x) = 0 and solve for x.
0 = f(x + 4) + 8
By subtracting 8 from both sides:
-8 = f(x + 4)
Since the exact value of x that makes f(x + 4) equal to -8. The x-intercept will depend on the behavior of f.
y-intercept:
The y-intercept of a function is the point where the graph intersects the y-axis, meaning the x-coordinate is zero (x = 0). To find the y-intercept of g(x), we substitute x = 0 into the function:
g(0) = f(0 + 4) + 8
g(0) = f(4) + 8
Again, the specific value of f(4) will depend on the behavior of the function f.
for such more question on function
https://brainly.com/question/14723549
#SPJ8
doc decides to buy the entire 6th grade a slice of pizza.
Answers
Answer:what
Step-by-step explanation:
Answer:
Sorry, This is not a question
Step-by-step explanation:
N/A
please answer the question below

Answers
Values for relation g are given in the table. Which ordered pair would be found in the inverse of g? X Y 2 2 3 5 4 9 5 13 A: (4,9) B:(-3.-5) C:(13,5) D:(-2,-2)
Answers
Answer:
D (13,5)
Step-by-step explanation:
X 2 3 4 5
Y 2 5 9 13
So the ordered pairs are (2,2),(3,5), (4,9), (5,13)
and the ordered pairs for the inverse are
(2,2),(5,3), (9,4), (13,5)
from which D (13,5) is found among the options.
Answer:
b
Step-by-step explanation:
No links please! Which expression has the same value as
Look below

Answers
Answer:
-5 1/3 - 3 1/3
Step-by-step explanation
both expressions equal -8 2/3
orthogonal projection onto plane 1 point possible (graded) find an expression for the orthogonal projection of a point onto a plane that is characterized by and . write your answer in terms of , and . (enter theta 0 for the offset . enter norm(theta) for the norm of a vector . use * to denote the dot product of two vectors, e.g. enter v*w for the dot product of the vectors and . )
Answers
This is the expression for the orthogonal projection of v onto the plane P characterized by θ and θ_0 is, proj_P(v) = [v₁ - (v₁ cos(θ) + v₂ sin(θ)) cos(θ), v₂ - (v₁ cos(θ) + v₂ sin(θ)) sin(θ)]
Let's assume that the plane P is given by the normal vector n = [cos(θ), sin(θ)], and a point on the plane is given by r = [cos(θ_0), sin(θ_0)].
To find the orthogonal projection of a point v onto P, we need to find the component of v that lies in the direction of the normal vector n, and then subtract that component from v. This can be done using the dot product of v and n:
proj_n(v) = (v · n) / ||n||^2 × n
where · denotes the dot product, ||n|| is the length of n, and proj_n(v) is the projection of v onto n.
To find the projection of v onto P, we need to subtract the projection of v onto n from v:
proj_P(v) = v - proj_n(v)
= v - (v · n) / ||n||^2 × n
Substituting the expressions for n and θ, we get:
proj_P(v) = v - (v · [cos(θ), sin(θ)]) / (cos^2(θ) + sin^2(θ)) × [cos(θ), sin(θ)]
= v - (v₁ cos(θ) + v₂ sin(θ)) / (cos^2(θ) + sin^2(θ)) × [cos(θ), sin(θ)]
= v - (v₁ cos(θ) + v₂ sin(θ)) / 1 × [cos(θ), sin(θ)]
= [v₁ - (v₁ cos(θ) + v₂ sin(θ)) cos(θ), v₂ - (v₁ cos(θ) + v₂ sin(θ)) sin(θ)]
where v₁ and v₂ are the components of v in the x and y directions, respectively. This is the expression for the orthogonal projection of v onto the plane P characterized by θ and θ_0.
Learn more about orthogonal projection here
brainly.com/question/29843133
#SPJ4
The given question is incomplete, the complete question is:
Find an expression for the orthogonal projection of a point v onto a plane P that is characterized by θ and θ_0. Write your answer in terms of v, θ and θ_0
If mZA = (4x - 2)° and mZB= (6x-20), what is the value of x?
Answers
To find the value of x, we can set the two angle measures equal to each other and solve for x.
Given:
mZA = (4x - 2)°
mZB = (6x - 20)°
Setting them equal to each other:
4x - 2 = 6x - 20
Now, we can solve for x:
4x - 6x = -20 + 2
-2x = -18
Dividing both sides by -2:
x = -18 / -2
x = 9
Therefore, the value of x is 9.
Answer:
The answer is 9.
Step-by-step explanation:
We need to use the fact that the sum of the angles in a triangle is 180 degrees. Let A, B, and C be the three angles in the triangle. Then we have:
mZA + mZB + mZC = 180°
Substituting the given values, we get:
(4x - 2)° + (6x - 20)° + mZC = 180°
Simplifying the left side, we get:
10x - 22 + mZC = 180°
Next, we use the fact that angles opposite congruent sides of a triangle are congruent. Since we know that segment AC and segment BC are congruent, we have:
mZA = mZB
Substituting the given values and simplifying, we get
4x - 2 = 6x - 20
Solving for x, we get:
x = 9
Therefore, the value of x is 9.
What is 5/8 divided by 1/4?
Answers
Answer: 2.5
Step-by-step explanation: If you do 5/8 divided by 1/4 in the calculator it is 2.5.
B
E
7
4
3
1
-2 -1 0
D
Determine the line of reflection.
O Reflection across x = 4
Reflection across y = 4
Reflection across the x-axis
Reflection across the y-axis
3
4
C
D'
8
E'
9
10
B'
A'
11
Answers
Answer: 10
Step-by-step explanation: it is a 5+ 5 =
5. Se hizo una encuesta a estudiantes, de una carrera de un total de 6000 estudiantes encuestados el 75% le gusta leer. ¿Cuántos estudiantes les gusta leer?
Answers
La encuesta indica que de entre todos los estudiantes de una carrera, 4500 les gusta leer.
PercentageThe percentage is the given definition for a fraction whose denominator is equal to 100. It is represented by %. See the example: \(\frac{30}{100} =\frac{3}{10}=0.3*100=30 \%\).
The question gives:
6000 students75% of students like to readThen, you will have:
\(6000\cdot \frac{75}{100}\\ \\ 6000\cdot \frac{3}{4}\\ \\ \frac{18000}{4} =4500\)
Read more about the percentage here:
brainly.com/question/24304697
#SPJ1
Find the slope of the line. Explain how you found your answer.

Answers
Answer: slope = 10/15
Step-by-step explanation: Identify two points in the graph
Make one of them (x1, y1) and the other (x2, y2)
Then use the slope equation:m= y2- y1/ x2 - x1
Sara started with 12 comic books in her collection. She collected the same number of comic books each month until she had 20 comic books in the 4th month. Ashton started with 2 comic books in his collection and continues to collect 3 comic books each month.
I NEED HELP PLEASE IM IN A TEST RN IF YOU GIVE ME THE CORRECT ANSWER I WILL GIVE U 70 PONITS
Answers
Sara and Ashton both have the same number of comic books after 10 months
How to determine when they both have the same number of books?From the question, we have the following parameters that can be used in our computation:
Sara
Initial = 12 comic books
Books at the fourth month = 20
Ashton
Initial = 2 comic books
Books each month = 3
The equations can be represented as
Total number of books = Initial + Books each month * Number of months
Rewrite as
y = Initial + Books each month * x
For Ashton, the equation is
y = 2 + 3x
For Sara, we have
y = 12 + Books each month * Number of months
So, we have
20 = 12 + Books each month * 4
This gives
Books each month = 2
So, the equation is
y = 12 + 2x
Substitute y = 2 + 3x in y = 12 + 2x
2 + 3x = 12 + 2x
Evaluate the like terms
x = 10
This means that
Number of months = 10
Hence, the number of months is 10
Read more about linear equations at
https://brainly.com/question/13738662
#SPJ1
Complete question
Sara started with 12 comic books in her collection. She collected the same number of comic books each month until she had 20 comic books in the 4th month. Ashton started with 2 comic books in his collection and continues to collect 3 comic books each month.
Calculate when they both have the same number of books
Question 2
A box contains 22 coloured pencils.
6 pencils are pink, 9 pencils are blue and 7 pencils are yellow.
Write down the ratio pink pencils : not pink pencils.
Give your answer in its simplest form.
Answers
Answer:
3/8 or 3:8
Step-by-step explanation:
pink : not pink
6 : 16
Think of it as a fraction. Simplify it in the same way.
6/16 simplifies to 3/8
So the pink:notpink ratio is 3/8 or 3:8
when simplified it becomes 3:8
What is the the value of x?
x/2
= 5
Answers
Answer:
10
Step-by-step explanation:
x/2 =5
2 x x/2 = 2 x 5
2x5 = 10
The ratio of good guys to bad guys was 13 to 6. If there were 78 good guys, How many bad guys were there?
Answers
Answer: 36
Step-by-step explanation:
78/13=6
6(6)=36
Dan ate at Applebee's and his check was 25.75. He wanted to leave a 20% tip. What was the total amount he paid for dinner?
Answers
Answer: $30.90
Step-by-step explanation:
Multiply 25.75 by .20 which gets you $5.15 which you add to $25.75 to get $30.90
Answer: $30.90
Step-by-step explanation:
1st way:
20% of $25.75 = $5.15
Add $25.75 and $5.15 together = $30.90
2nd way:
100% + 20% = 120%
120% of $25.75 = $30.90
Which statement is true about quadrilateral ABCD with vertices A(2, 8), B(3, 11), C(4, 8), and D(3, 5)?
Answers
Answer:
The quadrilateral is a rhombus
Step-by-step explanation:
Given
\(A = (2, 8)\)
\(B = (3, 11)\)
\(C = (4, 8)\)
\(D=(3, 5)\)
Required
The true statement
Calculate slope (m) using
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
Calculate distance using:
\(d= \sqrt{(x_2 - x_1)^2 + (y_2 -y_1)^2}\)
Calculate slope and distance AB
\(m_{AB} = \frac{11 - 8}{3 - 2}\)
\(m_{AB} = \frac{3}{1}\)
\(m_{AB} = 3\) -- slope
\(d_{AB}= \sqrt{(3 - 2)^2 + (11 -8)^2}\)
\(d_{AB}= \sqrt{10}\) -- distance
Calculate slope and distance BC
\(m_{BC} = \frac{8 - 11}{4 - 3}\)
\(m_{BC} = \frac{- 3}{1}\)
\(m_{BC} = -3\) -- slope
\(d_{BC} = \sqrt{(4-3)^2+(8-11)^2\)
\(d_{BC} = \sqrt{10}\) --- distance
Calculate slope CD
\(m_{CD} = \frac{5 - 8}{3 - 4}\)
\(m_{CD} = \frac{- 3}{- 1}\)
\(m_{CD} = 3\) -- slope
\(d_{CD} = \sqrt{(3-4)^2+(5-8)^2}\)
\(d_{CD} = \sqrt{10}\) -- distance
Calculate slope DA
\(m_{DA} = \frac{8 - 5}{2 - 3}\)
\(m_{DA} = \frac{3}{- 1}\)
\(m_{DA} = -3\) -- slope
\(d_{DA} = \sqrt{(2-3)^2 + (8-5)^2}\)
\(d_{DA} = \sqrt{10}\)
From the computations above, we can see that all 4 sides are equal, i.e. \(\sqrt{10}\)
And the slope of adjacent sides are negative reciprocal, i.e.
\(m_{AB} = 3\) and \(m_{CD} = -3\)
\(m_{CD} = 3\) and \(m_{DA} = -3\)
The quadrilateral is a rhombus
