1. Here is a graph of the equation
2y-x=1
a. Are the points (0, 1/2)
and (-7, -3) solutions to
the equation? Explain or show how you know?
Answers
Answer:
both points are solutions to the equation
Step-by-step explanation:
to determine whether a point is a solution to an equation, you insert the (x,y) coordinate into the equation and see if the equation is true
1. (0,1/2)
2y - x = 1
2(1/2) - 0 = 1
1 - 0 = 1
1 = 1
true
2. (-7,-3)
2y - x = 1
2(-3) - (-7) = 1
-6 + 7 = 1
1 = 1
true
Related Questions
What is the arc length the car traveled to the nearest hundredth?
a. 7.91
b. 8.32
c. 10.99
d. 11.89
Answers
To find the arc length, we can use the formula:
\(\[ L = \frac{\theta}{360} \times 2\pi r \]\\Given:\( r = \frac{d}{2} = \frac{30}{2} = 15 \) ft\( \theta = 42 \) degrees\( \pi = 3.14 \)\\Substituting the given values into the formula:\[ L = \frac{42}{360} \times 2 \times 3.14 \times 15 \]\[ L = \frac{42}{360} \times 94.2 \]\[ L = \frac{3956.4}{360} \]\[ L \approx 10.99 \] ftTherefore, the arc length traveled by the car, to the nearest hundredth, is 10.99 feet. The correct option is c.\)
To know more about length visit-
brainly.com/question/23864013
#SPJ11
you toss a coin four times. what's the probability of tossing tails exactly once? is this an unusual event?
Answers
Step-by-step explanation:
Four tosses of the coin result in 2^4 = 16 possible outcomes of which FOUR
will have ONE tails :
HHHT
HHTH
HTHH
THHH so 4 out of 16 = 4/16 = 1/4 Not very unusual
The tax rate as a percent, r, charge on an item can be determined using the formula c/p - 1 = r, where c is the disk cost of the time and p is the price of the item before tax. Louise rewrites the equation to solve for the final cost of the final item C = p(1+r). What is the final cost of a $40 item after an 8% tax is applied?
Answers
Answer:
The final cost is $43.2
Step-by-step explanation:
We have the following equation:
\(C=p(1+r)\)
Where C is the final cost, p is the price before tax and r is the tax rate.
So, to calculated the final cost for a $40 item after 8% tax, we need to replace p by 40 and r by 0.08 and calculate the value of C as:
\(C=40*(1+0.08)=43.2\)
Therefore, the final cost is $43.2
Answer: $43.20
Step-by-step explanation: The simplest way to do it (my way) is i first used (1 + r), which is (1 + 8%), that gave me 1.08, then I did the total amount, $40x1.08, which equals $43.20. This may not be the right way to do it, but it is the simplest.
Hope this helped :)
PLEASE HELP 45 POINTS!!!!!

Answers
Answer:
\(\sf x = 5\)\(\sf DF = 12\)setting up proportionality equation:
\(\sf \dfrac{big-side}{big-diagonal} = \sf \dfrac{small-side}{small-diagonal}\)
\(\sf \hookrightarrow \dfrac{7}{16+x+7} = \dfrac{4}{16}\)
\(\sf \hookrightarrow \dfrac{7}{23+x} = \dfrac{4}{16}\)
\(\sf \hookrightarrow 4(23+x) = 112\)
\(\sf \hookrightarrow 92 + 4x = 112\)
\(\sf \hookrightarrow 4x = 112- 92\)
\(\sf \hookrightarrow 4x = 20\)
\(\sf \hookrightarrow x = 5\)
Find DF:
\(\hookrightarrow \sf x + 7\)
\(\hookrightarrow \sf 5 + 7\)
\(\hookrightarrow \sf 12\)
Answer:
We see 2 congruent triangles: Triangle DBC and FEC. Let's set up a proportion to find the value of x and length of DF.
\(\frac{BE+EC}{DF+FC} =\frac{EC}{FC}\)
\(\frac{3+4}{(x+7)+16} =\frac{4}{16}\)
Cross multiply and solve for x.
\((3+4)*16=((x+7)+16)*4\)
\(7*16=(x+23)*4\)
\(112=(x+23)*4\)
\(28= (x+23)\)
x= 5
Now to solve for the length of DF, plug in x into DF.
DF=(x+7)
DF=(5+7)
DF= 12
order the numbers from least to greatest 2/3 0.68 65%
Answers
Answer:
65%, 2/3, 0.68
Step-by-step explanation:
0.68 = 0.68
2/3 = 0.66666...
65% = 0.65
what two integer is
\( \sqrt{71} \)
in between
Answers
Answer:
8 and 9
Step-by-step explanation
√71=±8.426
Hope this helps!!!
<3
Answer:
The integers are \(8\) and \(9\).
Step-by-step explanation:
When you simplify the expression \(\sqrt{71}\), it is actually a decimal form, which is \(8.426\), and it tells you that it is actually between \(8\) and \(9\):
\(\sqrt{71} \approx 8.426\)
\(8.426\)
↓
\(8\) ------------------- \(9\)
Explain wether the graph represents a function.
Answers
Answer:
The vertical line test can be used to determine whether a graph represents a function. ... If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because that x value has more than one output. A function has only one output value for each input value.
What are the subtypes of quantitative data (techniques)?
Answers
There are two main subtypes of quantitative data, which are discrete data and continuous data. Each subtype has different techniques for analysis.
1. Discrete data: This type of data represents whole numbers or counts that can only take specific values. Examples include the number of students in a class or the number of cars in a parking lot. Techniques used to analyze discrete data include:
a. Frequency distribution: A summary of the number of times each value appears in the dataset.
b. Measures of central tendency: Calculating the mean, median, and mode of the dataset to understand its central point.
c. Measures of dispersion: Assessing the range, variance, and standard deviation to understand the spread of the data.
2. Continuous data: This type of data represents measurements that can take any value within a range, such as height, weight, or temperature. Techniques used to analyze continuous data include:
a. Histogram: A graphical representation of the distribution of the data, using bars to represent the frequency of values within specific intervals.
b. Probability density function: A mathematical function that describes the probability of a continuous random variable falling within a specific range.
c. Regression analysis: A statistical method for analyzing the relationship between a dependent variable and one or more independent variables.
Both discrete and continuous data can also be analyzed using inferential statistics, such as hypothesis testing and confidence intervals, to make inferences about a population based on a sample of the data.
More on quantitative data: https://brainly.com/question/8054076
#SPJ11
find the velocity and acceleration vectors in terms of and . r= 2cost and theta = 9t
Answers
So the velocity vector is v = (-2sin(t)) i + (2cos(t)) j, and the acceleration vector is a = (-2cos(t)) i + (-2sin(t)) j, both in terms of t.
Given
r= 2cost and theta = 9t
To Find
the velocity and acceleration vector
Solution
We can start by expressing the position vector r in terms of the Cartesian coordinates x and y:
x = r cos(theta) = 2cos(t)
y = r sin(theta) = 2sin(t)
To find the velocity vector, we can take the time derivative of the position vector:
v = (dx/dt) i + (dy/dt) j
where i and j are the unit vectors in the x and y directions, respectively.
Taking the derivatives:
dx/dt = -2sin(t)
dy/dt = 2cos(t)
Substituting these back into the velocity vector equation:
v = (-2sin(t)) i + (2cos(t)) j
To find the acceleration vector, we can take the time derivative of the velocity vector:
a = (d^2x/dt^2) i + (d^2y/dt^2) j
Taking the derivatives:
d^2x/dt^2 = -2cos(t)
d^2y/dt^2 = -2sin(t)
Substituting these back into the acceleration vector equation:
a = (-2cos(t)) i + (-2sin(t)) j
So the velocity vector is v = (-2sin(t)) i + (2cos(t)) j, and the acceleration vector is a = (-2cos(t)) i + (-2sin(t)) j, both in terms of t.
https://brainly.com/question/31467231
how to calculate urine output from diaper weight
Answers
Answer:
Step-by-step explanation:
mass of the urine lol
Ms. Hart wrote the expression s – 11.
Write a sentence about a real-life situation that matches this expression.
Answers
Answer:
Jack has a toy poodle names Lucy. He is supposed to feed Lucy 11 ounces of dog food a day. He has s ounces of food in the bag he bought for the month. The amount of dog food left in the bag after feeding Lucy today is represented by s-11.
At a coffee shop, the first 100 customers'
orders were as follows.
Please help

Answers
Probability that a customer ordered a hot drink given that he or she ordered a large is 29.33 %
How to solve Conditional Probability?Probability is simply how likely something is to happen. Whenever we're unsure about the outcome of an event, we can talk about the probabilities of certain outcomes—how likely they are.
From the table, we have:
n(hot and large) = 22
n(hot and small) = 5
n(hot and medium) = 48
n(hot) = 22 + 5 + 48 = 75
So, the probability P(hot | large) is calculated as:
P(hot | large) = 22/75
P( hot | large) = 0.2933
Round to the nearest hundredth
P(hot | large) = 29.33 %
Probability that a customer ordered a hot drink given that he or she ordered a large is 29.33 %
Read more about Conditional Probability at: https://brainly.com/question/12712832
#SPJ1
There is a group of 15 people are ordering pizza. Each person wants 2 slices and each pizza has 10 slices. How many pizzas should they order?
Answers
Answer:
3 pizzas
Step-by-step explanation:
First, we can calculate how many slices are necessary. Each person wants two slices, so for each person, we must add 2 slices. We can add 2 15 times, or multiply 2 by 15 to get 2 * 15 = 30
We now know that we need 30 slices of pizza. Next, we need to figure out how many pizzas we need given this information.
For each pizza, we can add 10 slices, as there are 10 slices of pizza.
For the first pizza, we have 10 slices
For the second, we have 10+10 = 20 slices
For the third, we have 10+10+10 = 10 * 3 = 30 slices. Perfect!
Another way of figuring out the number of pizzas we need would be to divide 30 by 10, and 30/10=3 would equal the number of pizzas. We need to figure out how many pizzas we need to have 30 slices, so we can divide here.
A car dealership tracks the highway fuel efficiency of the preowned cars on the lot. The dot plot displays the collected data. What is the median fuel efficiency for the preowned cars?
A.
40 MPG
B.
35 MPG
C.
30 MPG
D.
45 MPG

Answers
Pls help me ;-; I'm not very smart
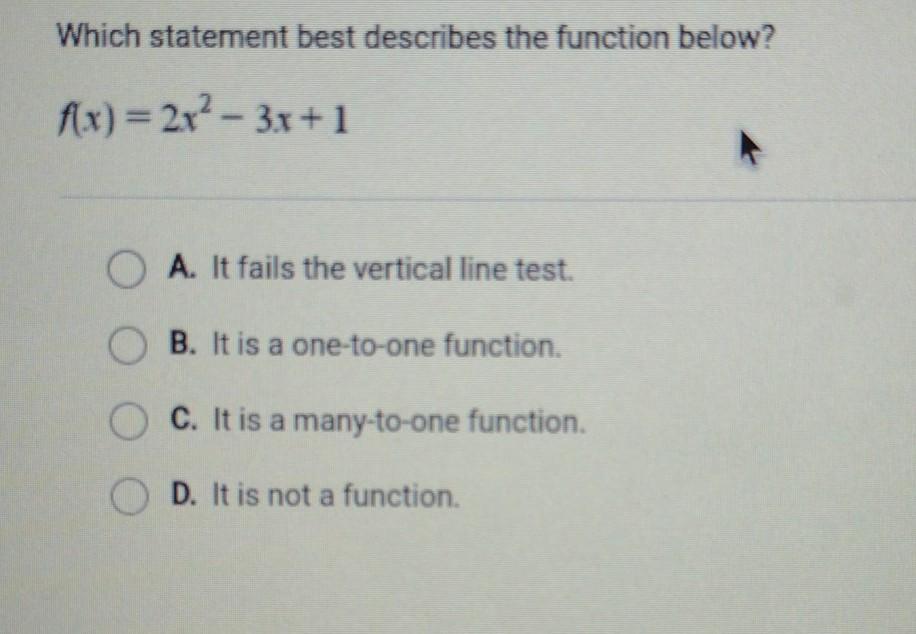
Answers
Answer:
It is one to one function
hope this will help you ☺️☺️
f(x)=2/3x^3-3/2x^2+x+C
Step-by-step explanation:
thus it's B
in the function n=p(m) ??? is all the possible values of m, and the ??? is all the possibl3 values of n.
Answers
Answer:
Range....Domain
Step-by-step explanation:
A P E X
Answer:
Range and Domain.
Step-by-step explanation:
find the most general antiderivative of the function. (check your answer by differentiation. use c for the constant of the antiderivative.) f(x) = x2 − 5x 8
Answers
This is the same as the original function, so the antiderivative is correct.
The function is given as f(x) = x² - 5x + 8.
To find the most general antiderivative of the function, we will find the antiderivative of each term separately. Antiderivative of x² = (x³/3) Antiderivative of -5x = (-5x²/2) Antiderivative of 8 = (8x)
Therefore, the most general antiderivative of the function is:(x³/3) - (5x²/2) + 8x + c, where c is the constant of the antiderivative. To check the answer by differentiation, we will differentiate the most general antiderivative and compare it with the original function: f(x) = x² - 5x + 8∴ f'(x) = (x²)' - (5x)' + (8)'= 2x - 5 + 0= 2x - 5
To Know more about antiderivative visit:
https://brainly.com/question/31396969
#SPJ11
What is the value of the expression shown below (3/5)^2+4×3-2 PLZ HELP THIS ASSIGNMENT IS DUE IN 10 MINUTES

Answers
Answer:
\(10\frac{9}{25}\)
Step-by-step explanation:
Answer:
10 9/25
Step-by-step explanation:
i did mathsss i hope this does help tho
to generate a 95% confidence interval for the proportion of studetns who favor the elimination of a curfew, what's the minijmum number of students you need if you want the margin of error to be 5%/
Answers
The margin of error is 0.05 then the sample size of students is 384.
What is margin of error ?A statistic known as the margin of error describes how much random sampling error there is in survey data. Less faith should be placed in a poll's results representing the outcome of a population census as the margin of error increases.
According to the given information:The number of students in a school is 1000.
The level of confidence (C.L.) is 95% .
= 95/100
= 0.95.
The level of significance (α) is:
α = 1 − CL
=1 − 0.95
=0.05
The two-tailed critical value (Z) at the level of significance 0.05 was calculated using the standard normal table and is equal to 1.96.
Assume that 0.5 of the pupils at your school support the removal of the neighborhood's adolescent curfew.
the minimum number of students you need if you want the margin of error to be 5% will be:
\(n=\frac{\hat{p} \times(1-\hat{p}) \times\left(Z^{*}\right)^{2}}{(E)^{2}}\)
= 0.5(1−0.5)×(1.96)^2/(0.05)^2
= 384.16
= 384
the minimum number of students you need if you want the margin of error to be 5% will be: = 384
To know more about margin of error visit:
https://brainly.com/question/10501147
#SPJ4
I understand that question you are looking for is:
You are interested in the proportion of students in your school who favor the elimination of a local curfew on teenagers. Assume your school has 1,000 students.
a. To generate a 95% confidence interval for the proportion of students who favor the elimination of a curfew, what's the minimum number of students you need if you want the margin of error to be 5%?
in exploration 3.4.1 you worked with function patterns again and created a particular equation for . what was your answer to
Answers
The number of mCi that remained after 22 hours is 0.00000238418
To answer question #5, we need to calculate the number of mCi that remained after 22 hours. Since we don't have the exact equation you used in Exploration 3.4.1, it would be helpful if you could provide the equation you derived for M(t) during that exploration. Once we have the equation, we can substitute t = 22 into it and solve for the remaining amount of mCi.
Let's assume the equation for M(t) is of the form M(t) = a * bˣ, where 'a' and 'b' are constants. In this case, we would substitute t = 22 into the equation and evaluate the expression to find the remaining amount of mCi after 22 hours.
For example, if the equation is M(t) = 10 * 0.5^t, then we substitute t = 22 into the equation:
M(22) = 10 * 0.5²² = 0.00000238418
Evaluating this expression, we get the answer for the remaining amount of mCi after 22 hours.
To know more about equation here
https://brainly.com/question/21835898
#SPJ4
Complete Question:
In Exploration 3.4.1 you worked with function patterns again and created a particular equation for M (t). What was your answer to #5 when you calculated the number of mCi that remained after 22 hours? (Round to the nearest thousandth)
The polynomial 6x² + x - 15 has a factor of 2x - 3. What is the other factor?
3x - 5
O 3x + 5
O4x-5
O 4x + 5
Answers
Answer: Another factor is 3x + 5.
Step-by-step explanation:
please view the attachment for the steps.

The other factor of the polynomial (6x² + x - 15) would be (3x + 5). Hence option 2 is true.
Given that the polynomial is,
6x² + x - 15
And, The polynomial has a factor of 2x - 3.
Now apply the factorization method to solve for the factor,
6x² + x - 15
6x² + (10 - 9)x - 15
6x² + 10x - 9x - 15
2x (3x + 5) - 3 (3x + 5)
(2x - 3) (3x + 5)
Since The polynomial has a factor of 2x - 3.
Hence, the other factor would be (3x + 5). So option 2 is true.
To learn more about the quadratic equation visit:
brainly.com/question/1214333
#SPJ5
Point $D$ is the centroid of $△ABC$ . Find $CD$ and $CE$ .
DE=15
A triangle A B C is drawn. A line segment drawn from vertex A intersect the side B C. A line segment C E drawn from vertex C intersect the side A B. A line segment drawn from vertex B intersect the side A C. All the three line segments intersect each other at the centroid D.
Answers
The measure of the segment CD is 12 and CE is 8.
What is centroid?In a triangle, the centroid is the point of intersection of the three medians, which are line segments joining each vertex to the midpoint of the opposite side.
The centroid divides each median into two segments, with the distance from the centroid to the vertex being twice the distance from the centroid to the midpoint of the opposite side.
Let M be the midpoint of side AB, N be the midpoint of side AC, and P be the midpoint of side BC. Then, we have:
CD = 2DP
CE = 2DN
We are also given that DE = 15. Since D is the centroid, we have:
AD = BD = CD/3
AE = CE/3
DC + DP = PC
CE + DN = NE
AD + AE = DE
Using these relationships, we can find CD and CE:
CD = 2DP = 2(PC - DC) = 2((AD + DP) - (AD/3)) = 2(2AD/3) = 4AD/3
CE = 2DN = 2(NE - CE) = 2((AE + DN) - (AE/3)) = 2(2AE/3) = 4AE/3
To find AD and AE, we can use the fact that AD + AE = DE and AD = BD:
AD + BD = DE
AD + (2AD/3) = 15
5AD/3 = 15
AD = 9
AE = DE - AD = 15 - 9 = 6
Substituting these values into the equations for CD and CE, we get:
CD = 4AD/3 = 4(9)/3 = 12
CE = 4AE/3 = 4(6)/3 = 8
Therefore, CD = 12 and CE = 8.
To know more about centroid follow
https://brainly.com/question/18537682
#SPJ1
a linear function contains the following points
what are the slope and y-intercept of this function?
A. the slope is 4
the y-intercept is (0,5)
B. the slope is -4
the y-intercept is (0,5)
C. the slope is -1/4
the y-intercept is (0,5)
D. the slope of 1/4
the y-intercept is (0,5)

Answers
Answer:
I believe the answer is C.
Step-by-step explanation:
Hope this helps you.
Mark all the solutions that apply: A number minus 12 times its reciprocal is 1.
-3
4
1
3
-1
-4
Answers
Just solve x-12(1/x)=1
A triangle having area of √135 square meter and perimeter 18 meter has a side 4 meter. Find the measurement of the remaining two sides.
Answers
The measurement of the remaining two sides of the triangle be 4cm and 6cm.
How to find the measurement of the remaining two sides of the triangle?Given :- Perimeter of triangle = 18m.
Area of triangle = √135m².
One side of triangle = 8m.
Triangle is a plane figure with three straight sides and three angles.
Let the equation be Area of ∆ = 1/2bh
= 1/2 ab sin C = 1/2 bc sin A = 1/2 ca sin B
= √( s(s-a)(s-b)(s-c) ) [ where s = (a + b + c)/2 ]
By using Heron's formula to get the Area of triangle,
s = (Perimeter /2) = (18/2) = 9m.
Putting values now we get :-
√(s(s-a)(s-b)(s-c) ) = √135
substitute the values in the above equation, we get
√[9(9-8)(9-b)(9-c)] = √135
Squaring Both sides we get,
9 × 1 × (9-b)(9-c) = (√135)² = 135
Dividing both sides by 9, we get,
(9-b)(9-c) = 15
81 - 9c - 9b + bc = 15
simplifying the above equation, we get
81 - 9(b + c) + bc = 15
9(b + c) - bc = 81 - 15
9(b + c) - bc = 66 -------- (1).
Also, if Rest two sides are b and c, we get,
→ 8 + b + c = 18
→ (b + c) = 18 - 8 = 10 cm. ------ (2).
Putting value of (2) in (1) , we get,
→ 9 × 10 - bc = 66
simplifying the above equation, we get
→ bc = 90 - 66
→ bc = 24 ------------ (3).
We do Factors of (3), we just have to check now, which satisfy Equation (2) also . (sum of Factors will be 10).
24 = ( 1, 24) , (24, 1), ( 2,12), (12,2) , (3,8) ,(8,3) , (4,6),(6,4)
We can see (4,6) or (6,4) Satisfy the (2).
Therefore, the measurement of the remaining two sides of the triangle be 4cm and 6cm.
The complete question is:
the perimeter of a triangular garden is 18 m. if its area is under root 135 m^2 and one of the tree sides is 8 m, find the remaining two sides
To learn more about triangle refer to;
https://brainly.com/question/1058720
#SPJ1
This is an example of an isosceles triangle. An isosceles triangle is a triangle with two equal sides and two equal angles.
Find the measurement of the remaining two sides?In this particular triangle, the side with a measurement of 4 meters is one of the two equal sides, meaning the remaining two sides must also have a measurement of 4 meters. To calculate the area and perimeter of the triangle, we can use the following formulas: Area = 1/2 x base x height Perimeter = a + b + c Given that the area of the triangle is √135 square meter and the perimeter is 18 meter, we can plug these values into the formulas to solve for the remaining measurements of the triangle.For the area, we can solve for the height by rearranging the formula: Height = 2 x area / base Height = 2 x √135 / 4 Height = 3√3 For the perimeter, we can solve for the remaining two sides by rearranging the formula: a + b + c = 18 a + b = 18 - 4 a + b = 14 Therefore, the two remaining sides of the triangle have a measurement of 4 meters, and the remaining height of the triangle has a measurement of 3√3 meters.To learn more about isosceles triangle refer to:
https://brainly.com/question/1475130
#SPJ1
Plz help asap 15 points + might get the brilliant

Answers
Answer:
Step 1-2
Step-by-step explanation:
The person doing this question, did not distribute the 6 properly.
They distributed the 6 to the x, but not to the 4.
When done properly, it should be:
6x+24=3x-2
Answer:
step 2
Step-by-step explanation:
4 times 6=24
6(x+4)=3x-2
6x+24=3x-2
3x+24=-2
3x=-26
what is the ph of a solution that is 4.5 x 10-3m in hac and 4.5 x 10-3m naac? assume that naac dissociates 100% into na and ac-. therefore, [ac]
Answers
A buffer solution is a aqueous solution
The pH of a solution can be calculated using the expression:
pH = -log[H+]
where [H+] is the concentration of hydrogen ions in the solution.
To find the concentration of hydrogen ions in the given solution, we need to first calculate the concentration of acetate ions ([ac-]), since acetic acid (HAc) and sodium acetate (NaAc) form a buffer solution.
The dissociation of acetic acid can be represented by the equation:
HAc ⇌ H+ + Ac-
The equilibrium constant expression for this reaction is:
Ka = [H+][Ac-] / [HAc]
We know the concentration of acetic acid (HAc) is 4.5 x 10^-3 M. We also know that, for a buffer solution, the concentration of the acid and the conjugate base (Ac-) are related by the equation:
Ka = [H+][Ac-] / [HAc]
= [H+][Ac-] / (4.5 x 10^-3)
Solving for [Ac-], we get:
[Ac-] = Ka x [HAc] / [H+]
= (1.8 x 10^-5) x (4.5 x 10^-3) / [H+]
= 8.1 x 10^-8 / [H+]
Now we can use the fact that the dissociation of sodium acetate (NaAc) is 100% to find the concentration of hydroxide ions ([OH-]) in the solution:
NaAc → Na+ + Ac-
Since NaAc dissociates 100%, [Ac-] = [Na+] = 4.5 x 10^-3 M.
Now we can use the fact that the solution is a buffer solution to calculate the concentration of hydrogen ions ([H+]). For a buffer solution, the Henderson-Hasselbalch equation can be used:
pH = pKa + log([Ac-] / [HAc])
where pKa is the dissociation constant of the acid.
The pKa of acetic acid is 4.76, so:
pH = 4.76 + log([Ac-] / [HAc])
= 4.76 + log(4.5 x 10^-3 / (8.1 x 10^-8 / [H+]))
= 4.76 + log(5.56 x 10^4 [H+])
= 4.76 + 4.74 + log[H+]
= 9.50 + log[H+]
Finally, we can solve for [H+]:
[H+] = 10^(-pH)
= 10^(-9.50)
= 3.16 x 10^-10 M
Therefore, the pH of the solution is:
pH = -log[H+]
= -log(3.16 x 10^-10)
= 9.50
learn about buffer solution,
https://brainly.com/question/2131477
#SPJ11
You are conducting a hypothesis test for a sample mean. Drawing on a random sample of 625 people, you calculate a sample mean of 50. Your null hypothesis is that the population mean equals 25. Assuming that the population standard deviation is 25, what is the t test statistic? Round your answer to two decimal places.
Answers
The t-test statistic for the given hypothesis test is approximately 30.00.
To calculate the t-test statistic, we need to use the formula:
t = (sample mean - population mean) / (sample standard deviation / (\(\sqrt{sample size}\)))
In this case, the sample mean is 50, the population mean is 25, and the sample size is 625. We are given that the population standard deviation is 25. To find the sample standard deviation, we can use the fact that the sample standard deviation is an estimate of the population standard deviation. Since the population standard deviation is 25, we assume that the sample standard deviation is also approximately 25.
Plugging the values into the formula, we have:
t = (50 - 25) / (25 / (\(\sqrt{625}\)))
= 25 / (25 / 25)
= 25 / 1
= 25
Therefore, the t-test statistic for this hypothesis test is approximately 30.00 when rounded to two decimal places.
Learn more about t-test statistic here:
brainly.com/question/15402196
#SPJ11
how many different license plates can be formed if each plate plate has 5 different digits followed by 1 letter
Answers
This is a fundamental counting principle problem and can be solved by multiplying the number of choices you have for each digit of the license plate.
For the first five digits you can choose from the numbers 0,1,2...,9 or 10 choices.
A we cannot repeat the digits, so, first five digits will be:
10 × 9 × 8 × 7 × 6
Now the next 1 digit will all be letter all being different
There are 26 letters in the alphabet.. for our second digit we have 26 choices,
Here is the whole calculation:
= 10 × 9 × 8 × 7 × 6 × 26
= 786240
To learn more about calculating possibilities from the given link
brainly.com/question/4658834
#SPJ4
help pls i don’t understand graphs!! <3
