1. Samuel made a 76% on his Algebra test. He got 22 questions correct. How many total questions
were on his Algebra test?
HELP PLEASE✨
Answers
Answer:
29 questions on his test
Step-by-step explanation:
set it up as fractions equal to each other so that you can solve for x
\(76\%= \frac{76}{100}\)
x is the total number of questions on the test
we know that samuel got 22 of those questions correct, and a grade is calculated by dividing the number of correct answers by the total number of questions, so we can write
\(\frac{76}{100}=\frac{22}{x}\)
then you can solve by cross multiplying
\(76x = 22 (100)\)
\(76x=2200\)
get the x by itself by dividing both sides by 76, and then you have x
\(\frac{76x}{76}=\frac{2200}{76}\)
\(x=\frac{2200}{76}=28.947\)
since you're not going to have .947 of a question, round it up to 29
and then you have it
\(x=29\)
Related Questions
Today only, a table is being sold at a 36% discount. The sale price is $592. What was the price yesterday?
Answers
The price of the table yesterday is $925
Explanation:The sale price of the table today = $592
Let yesterday's sale price be x
Discount = 36%
The percentage sale price today = 100% - 36%
The percentage sale price today = 64%
Today's sale price = 64% of yesterday's sale price
592 = (64/100)x
592 = 0.64x
x = 592/0.64
x = $925
The price of the table yesterday is $925
Pls help
Write the equation for a parabola with a focus at (-4,3) and a directrix at y=5
Answers
Answer:
y=(1/-4)(x+4)^2 +4
Step-by-step explanation:
Don't ask
I'm stuck with my math word problem pls helped me
2/2
Answers
Answer:
A. \(\frac{c}{11} *7-48\)
Step-by-step explanation:
myopenmath.comSuppose that 14% of people own dogs. If you pick two people at random, what is the probability thatthey both own a dog?Give your answer as a decimal rounded to 4 places.CalculatorScratchwork Area

Answers
Answer:
\(0.0196\)Explanation:
The statement "Suppose that 14% of people own dogs," implies that the probability of owning a dog is given as;
\(Pr(Dog\text{ Owner) =}\frac{14}{100}\)Therefore, if two people are selected randomly for owning dogs, they would have the same probability attached to them.
We can then combine both probabilities by using the "and" symbol. which implies "multiplication."
Workings
\(\begin{gathered} pr(2\text{ dog owners) =}\frac{14}{100}\times\frac{14}{100} \\ =\frac{196}{10000} \\ =0.0196 \end{gathered}\)
Fill in the table using this function rule
f(x)=√x+9
Simplify your answers as much as poss
Click "Not a real number" if applicable.
X
-22
-18
-9
55
f(x)
0
0
0

Answers
The table would be filled by the following;
1) Not a real number
2) Not a real number
3) 0
4) 8
How do we fill the table?
An expression or equation that specifies the operation or operations applied to the input to produce the output is the common format for a function rule. It illustrates the mathematical relationship between the input and output, or independent and dependent variables.
We have the rule;
f(x)=√x+9
1) √(-22) + 9 - Not a real number
2) √(-18) + 9 Not a real number
3) √(-9) + 9 = 0
4) √55 + 9 = 8
Learn more about function rule:https://brainly.com/question/10705186
#SPJ1
Take the first 4 digits of your student number as the first number and the last 3 digits as the second number. Write the matlab code to find the greatest common divisor of these numbers using the Euclidean algorithm.
Answers
The required Matlab code to find the greatest common divisor of a number using the Euclidean algorithm is shown.
To find the greatest common divisor (GCD) of two numbers using the Euclidean algorithm in MATLAB, you can use the following code:
% Replace '12345678' with your actual student number
studentNumber = '12345678';
% Extract the first 4 digits as the first number
firstNumber = str2double(studentNumber(1:4));
% Extract the last 3 digits as the second number
secondNumber = str2double(studentNumber(end-2:end));
% Find the GCD using the Euclidean algorithm
gcdValue = gcd(firstNumber, secondNumber);
% Display the result
disp(['The GCD of ' num2str(firstNumber) ' and ' num2str(secondNumber) ' is ' num2str(gcdValue) '.']);
Make sure to replace '12345678' with your actual student number. The code extracts the first 4 digits as the first number and the last 3 digits as the second number using string indexing. Then, the gcd function in MATLAB is used to calculate the GCD of the two numbers. Finally, the result is displayed using the disp function.
Learn more about Matlab code here:
https://brainly.com/question/30763780
#SPJ4
among the 500 regular customer of shop .250 of them regularly buy product A . 250 customer regular buy product B . If 20 customer by neither of the products . then what is the number of customer that regularly buy only product A
Answers
We can solve this problem by using the formula for the number of elements in the union of two sets:
n(A U B) = n(A) + n(B) - n(A ∩ B)
where n(A) represents the number of elements in set A, n(B) represents the number of elements in set B, and n(A ∩ B) represents the number of elements in the intersection of sets A and B.
In this case, we have:
n(A) = 250
n(B) = 250
n(A U B) = 500 - 20 = 480
Substituting these values into the formula, we get:
480 = 250 + 250 - n(A ∩ B)
Solving for n(A ∩ B), we get:
n(A ∩ B) = 250 + 250 - 480 = 20
So, the number of customers who regularly buy both products A and B is 20.
To find the number of customers who regularly buy only product A, we can subtract the number of customers who regularly buy both products A and B from the total number of customers who regularly buy product A:
n(A) - n(A ∩ B) = 250 - 20 = 230
Therefore, the number of customers who regularly buy only product A is 230.
Combine like terms to create an equivalent expression.
Make sure to simplify coefficients and constants as well.
-\dfrac65-\dfrac23v+\dfrac{4}{15}+\dfrac13v−
5
6
−
3
2
v+
15
4
+
3
1
v
Answers
Answer is in the file below
tinyurl.com/wpazsebu
Your Welcome!!!!
The answer is in the picture!!!! :3

IQ scores are normally distributed with a
mean of 100 and a standard deviation of
15. What percentage of people have an IQ
score less than 117, to the nearest tenth?
Answers
Answer: To find the percentage of people with an IQ score less than 117, we need to calculate the z-score first. The z-score measures how many standard deviations an individual score is from the mean in a normal distribution.
The z-score formula is given by:
z = (x - μ) / σ
Where:
x = IQ score (117 in this case)μ = mean IQ score (100)σ = standard deviation (15)
Let's calculate the z-score:
z = (117 - 100) / 15z = 17 / 15z ≈ 1.1333
Now, we need to find the percentage of people with a z-score less than 1.1333. We can look up this value in the standard normal distribution table (also known as the Z-table) or use statistical software/tools.
Using the Z-table, we find that the percentage of people with a z-score less than 1.1333 is approximately 0.8708, or 87.08% (rounded to the nearest hundredth).
Therefore, approximately 87.1% of people have an IQ score less than 117.
if two bodies of masses 2000 kg and 4000 kg are separated by a distance of 10m the gravitational force attraction between them is a)6.67×10‐¹¹N
b)48.85×10^7N
c)53.36N
d)53.36×10^‐7N
Answers
Answer:
d)53.36×10⁻⁷N
Step-by-step explanation:
The formula for gravitational force between two bodies is given by
F = G (Mm/r²)
Where,
F = gravitational force ( we are asked to find this)
G = gravitational constant = 6.674 x 10⁻¹¹
M = mass of one of the bodies = 4000 kg
m = mass of the the other body = 2000 kg
r = distance between the two bodies = 10m
substituting the above values into the equation:
F = G (Mm/r²)
= (6.674 x 10⁻¹¹) (4000)(2000) / (10²)
= 5.339 x 10⁻⁶
= 53.39 x 10⁻⁷ Newtons
The closest answer to this is d
A drug is reported to benefit 40% of the patients who take it. If 6 patients take the drug, what is the probability that 4 or more patients will benefit?
Answers
The probability that 4 or more patients out of 6 will benefit from the drug is approximately 0.256, or 25.6%.
To calculate the probability that 4 or more patients will benefit from the drug out of 6 patients who take it, we can use the binomial probability formula. Let's break down the steps to determine this probability:
The drug is reported to benefit 40% of the patients who take it. This means that the probability of a patient benefiting from the drug is 0.40, or 40%.
We want to find the probability that 4 or more patients out of 6 will benefit from the drug. To do this, we need to calculate the probability of 4, 5, and 6 patients benefiting, and then sum those probabilities.
We can use the binomial probability formula to calculate these probabilities. The formula is given by P(X = k) = (nCk) * p^k * (1 - p)^(n - k), where P(X = k) is the probability of getting exactly k successes, n is the total number of trials, p is the probability of success, and (nCk) is the binomial coefficient.
Let's calculate the probability of 4 patients benefiting from the drug. Using the binomial probability formula:
P(X = 4) = (6C4) * (0.40)^4 * (1 - 0.40)^(6 - 4)
Simplifying the calculation:
P(X = 4) = 15 * (0.40)^4 * (0.60)^2
Let's calculate the probability of 5 patients benefiting from the drug:
P(X = 5) = (6C5) * (0.40)^5 * (1 - 0.40)^(6 - 5)
Simplifying the calculation:
P(X = 5) = 6 * (0.40)^5 * (0.60)^1
Finally, let's calculate the probability of 6 patients benefiting from the drug:
P(X = 6) = (6C6) * (0.40)^6 * (1 - 0.40)^(6 - 6)
Simplifying the calculation:
P(X = 6) = 1 * (0.40)^6 * (0.60)^0
Now, we can calculate the probability that 4 or more patients will benefit by summing the individual probabilities:
P(X ≥ 4) = P(X = 4) + P(X = 5) + P(X = 6)
Substituting the calculated values:
P(X ≥ 4) = (15 * (0.40)^4 * (0.60)^2) + (6 * (0.40)^5 * (0.60)^1) + (1 * (0.40)^6 * (0.60)^0)
Simplifying the calculation:
P(X ≥ 4) = 0.1536 + 0.0768 + 0.0256
P(X ≥ 4) = 0.256
Therefore, the probability that 4 or more patients out of 6 will benefit from the drug is approximately 0.256, or 25.6%.
Learn more about probability here
https://brainly.com/question/13604758
#SPJ11
Last week Jeremy spent $20 on cheese for his family. This week his son Ryan was away on a band trip, causing his cheese bill to decrease by 34.4%. By how much money did his cheese bill decrease this week? What is his total cheese bill for this week?The cheese bill decrease this week by $.The total cheese bill for this week was $
Answers
To solve this problem, we have to determine the 34.4% of 20. To find the x% of y, we can use the following expression:
\(y*\frac{x}{100}.\)Therefore, the 34.4% of 20 is:
\(20*\frac{34.4}{100}=6.88.\)Subtracting the above amount from20, we get:
\(20-6.88=13.12.\)Answer:
The cheese bill decreased this week by
\(6.88\text{ dollars.}\)The total cheese bill for this week is:
\(13.12\text{ dollars.}\)(23 pts) Let X and Y have joint density f XY (x,y)=24xy f XY (x,y)=\ matrix 24xy&x>=0,y>=0,x+y<=1\\ 0&otherwise matrix
Find the marginal density of X / Y
(1)
Answers
To find the marginal density of X/Y, we need to integrate the joint density function fXY(x, y) over the range of Y. By performing the integration, we obtain the marginal density of X/Y as a function of X. The resulting marginal density provides information about the distribution of the ratio X/Y.
The marginal density of X/Y can be obtained by integrating the joint density function fXY(x, y) over the range of Y. In this case, the joint density function is given by:
fXY(x, y) =
24xy if x >= 0, y >= 0, and x + y <= 1
0 otherwise
To find the marginal density of X/Y, we integrate fXY(x, y) with respect to y, while keeping x as a constant. The integration limits for y can be determined based on the given conditions x >= 0, y >= 0, and x + y <= 1. Since y must be non-negative, the lower limit of integration is 0. The upper limit of integration can be determined by the constraint x + y <= 1, which implies y <= 1 - x.
Integrating fXY(x, y) over the range of y, we obtain the marginal density of X/Y as follows:
fX/Y(x) = ∫[0 to (1 - x)] 24xy dy
Evaluating the integral, we have:
fX/Y(x) = 24x * ∫[0 to (1 - x)] y dy
= 24x * [(y^2)/2] evaluated from 0 to (1 - x)
= 12x * (1 - x)^2
The resulting marginal density fX/Y(x) represents the distribution of the ratio X/Y. It provides information about the likelihood of different values of X/Y occurring. The shape of the distribution can be further analyzed to understand the characteristics of the random variable X/Y.
To learn more about function click here: brainly.com/question/30721594
#SPJ11
PLEASE HELP 50 POINTS! I REALLY NEED THIS

Answers
The required order of solution for the given system equation,
1 No solution
2 Many solutions
3 One solution
4 No solution
Given a system of equations,
(1)
y = 5x + 7
3y -15x = 18
Since the slope of the equations are equal so this equation has no solution
(2)
x - 2y = 6
3x - 6y = 18
Since the slope of the equations is equal and also has an equal intercept so this equation has many solutions.
(3)
y=3x+6
y = -1/3x - 4
The slope of the equation of this line is the negative reciprocal of the other implying these lines are perpendicular to each other and have one solution.
(4)
y = 2/3x -1
y = 2/3x -2
Since the slope of the equations is equal so this equation has no solution.
Learn more about the solution to the equation here:
https://brainly.com/question/14603452
#SPJ1
Kate is a buyer for a men’s fashion retail store. She will order a new cloth overcoat from Paris for the fall fashion season. Based on her experience, she expects to sell at least 100 coats, and at most 400, but she feels that any number of sales in between is equally likely. Therefore, she estimates that her sales are uniformly distributed between 100 and 400. The total cost to the store is $100 per coat, and the retail price is set at $180. Any coats left over at the end of season would be sold at $60 each.
part 1: a) How many coats should Kate buy if she wants to maximize profits?
part 2: b) Assume Kate buys the number of coats suggested in part a), what is the probability that the coats sell out? What is the probability that they do not sell out?
Answers
Part 1: Kate should buy 100 coats to maximize profits.Part 2: The probability that the coats sell out is 0.25 (25%), and the probability that they do not sell out is 0.75 (75%).
To maximize profits, Kate should consider the scenario where she sells all the coats without any left over at the end of the season.
Since the sales are uniformly distributed between 100 and 400, buying 100 coats ensures that she meets the minimum expected sales of 100. Purchasing more than 100 coats would increase costs without a guarantee of higher sales, potentially leading to excess inventory and lower profits.
Given that the sales are uniformly distributed between 100 and 400 coats, Kate's purchase of 100 coats covers the minimum expected sales.
The probability of selling out can be calculated by finding the proportion of the range covered by the desired sales (100 out of 300). Therefore, the probability of selling out is 100/300 = 0.25 or 25%. The probability of not selling out is the complement, which is 1 - 0.25 = 0.75 or 75%.
learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
What is the easiest way to solve negative fractions plus positive fractions?
Answers
Answer:
Step-by-step explanation:
and I'll explain why so when when we're
looking into combining fractions
positive negative fractions the main
important thing we need to make sure we
have is like denominators
all right common dinar common
denominator the easiest the easiest way
to find a common denominator is to
multiply the denominators right that's
the easiest way to go ahead and find one
just multiply three times eight which is
24 that's gonna give you your comments
and on there does that make sense so
make sense multiply the denominator but
that's not always going to be the least
common denominator so an easy way to
always check to find the least common
denominator is choose the largest
denominator which would be 8 and then
kind of list out the multiples so is and
sitting determine it does 3 divide into
any of those multiples before we get to
24 so just 3 to buy an 8 no so 8 is not
the least common denominator then we go
to 16 just 3 divided into 16 No
24 yes it does so actually end up 3
times 8 is gonna equal 24 and it's okay
lays knowing if you always want to
multiply your denominators you can
always do that but that just because
you're multiplying you're not always
gonna get the least common denominator
and the problem with that is you're
gonna have to simplify your fraction a
little bit more at the end all right but
it is also a way to always get a common
denominator so my lcd is 24 and what I
like you guys to do is always like write
that down so you can always kind of
remember it and basically when we have
an LCD of 24 what we want to be able to
do is say alright what do I need to
multiply now both of my denominators by
to get to 24 well to get 3 forget about
the negative sign per second for do get
3 we need to multiply by 8 right but
there's a problem if you have a fraction
and you only multiply the denominator by
it you've now changed the fraction think
about 1/2 if you have 1/2 and you
multiply the denominator by 3 you now
have 1/6 right is 1/6 equal to 1/2
no so we need to multiply the numerator
and the denominator by 8 think about
again 1/2 times 3 over 3 equals 3 over 6
is 3 over 6 equivalent to 1/2 yes so
when you're multiplying your fraction we
want to make sure we
keep equivalent fractions for 3/8 we
need to multiply by five over five and
then when I multiply fractions I just
simply multiply across numerator times
numerator denominator times denominator
therefore I get negative 8 over 24 plus
I don't know 3 right thank you I don't
know I was like off in my own world I
guess there you go
sorry so therefore now I have negative 8
24 plus 9 over 24 and now when we need
to add combined fractions we need to
combine fractions as long as they have
common denominators we just add or
subtract our numerators so just think
about negative you owe eight dollars you
have nine dollars in your pocket
therefore you're gonna have one dollar
left right and you keep the denominator
the same question okay letting it
internalize
True or False:
(2x2 - 3x) - (4x2 - x) = -2x2 - 2x
Answers
yeah it’s true
Find a vector parameterization for the line passing through (1, 1, -1) and (6, -9, 4).
Answers
The vector parameterization for the line passing through the points (1, 1, -1) and (6, -9, 4) is:
x = 1 + 5t
y = 1 - 10t
z = -1 + 5t
To find a vector parameterization for the line passing through the points (1, 1, -1) and (6, -9, 4), we can use the vector equation of a line:
r = a + t * d
where r is the position vector of any point on the line, a is a known point on the line, t is a parameter, and d is the direction vector of the line.
First, let's find the direction vector d. We can subtract the coordinates of the two points to obtain the direction vector:
d = (6, -9, 4) - (1, 1, -1)
= (5, -10, 5)
Now, we can choose one of the given points, say (1, 1, -1), as our known point a.
Substituting these values into the vector equation, we have:
r = (1, 1, -1) + t * (5, -10, 5)
So, the vector parameterization for the line passing through the points (1, 1, -1) and (6, -9, 4) is:
x = 1 + 5t
y = 1 - 10t
z = -1 + 5t
where t is a real number that can vary to give different points along the line.
learn more about parameterization here
https://brainly.com/question/14762616
#SPJ11
The radius of a circle is increasing at a rate of 8 centimeters per minute. Find the rate of change of the area when the radius is 2 centimeters. Round your answer to one decimal place.
Answers
The rate of change of the area when the radius is 2 centimeters is approximately 100.5 square centimeters per minute.
To find the rate of change of the area of a circle when the radius is 2 centimeters, we need to use the formula for the area of a circle, which is \(A = πr^2.\)
We know that the radius is increasing at a rate of 8 centimeters per minute, so we can use this information to find the rate of change of the area.
We can start by finding the area of the circle when the radius is 2 centimeters. Substituting r = 2 into the formula, we get:
A = π(2)^2
A = 4π
So the area of the circle is 4π square centimeters when the radius is 2 centimeters.
Now, let's find the derivative of the area with respect to time. Using the power rule of differentiation, we get:
dA/dt = 2πr (dr/dt)
Substituting r = 2 and dr/dt = 8, we get:
dA/dt = 2π(2)(8)
dA/dt = 32π
So the rate of change of the area when the radius is 2 centimeters is 32π square centimeters per minute. To round this to one decimal place, we can use a calculator to get:
dA/dt ≈ 100.5
Therefore, the rate of change of the area when the radius is 2 centimeters is approximately 100.5 square centimeters per minute.
Learn more about centimeters here:
https://brainly.com/question/19098836
#SPJ11
three airlines serve a small town in ohio. airline a has 53% of all scheduled flights, airline b has 32% and airline c has the remaining 15%. their on-time rates are 82%, 64%, and 36%, respectively. a flight just left on-time. what is the probability that it was a flight of airline a?
Answers
The probability that it was a flight of airline A is equal to approximately 0.6268, or about 62.68%
Let A, B, and C be the events that a flight is operated by airlines A, B, and C, respectively.
And let O be the event that a flight is on-time.
The conditional probability of A given O is equal to P(A|O).
Using Bayes' theorem, we have,
P(A|O) = P(O|A) × P(A) / P(O)
where P(O|A) is the probability that a flight of airline A is on-time.
P(A) is the probability that a flight is operated by airline A.
And P(O) is the probability that a flight is on-time regardless of which airline operates it.
Calculate these probabilities as follows,
P(O|A) = 0.82, the on-time rate of airline A
P(A) = 0.53, the proportion of flights operated by airline A
P(O) = P(O|A) × P(A) + P(O|B) × P(B) + P(O|C) × P(C)
= 0.82 × 0.53 + 0.64 × 0.32 + 0.36 × 0.15
= 0.6934
Plugging in these values, we get,
P(A|O) = 0.82 × 0.53 / 0.6934
Simplifying it,
P(A|O) = 0.6268
Therefore, the probability that the on-time flight that just left was operated by airline A is approximately 0.6268, or about 62.68%.
learn more about probability here
brainly.com/question/13720719
#SPJ4
Longitud de circunferencia si diámetro es 32cm
Answers
Por lo tanto, la longitud de la circunferencia con un diámetro de 32 cm sería aproximadamente 100.53 cm.
How to solve for the circumferenceLa fórmula para calcular la longitud de una circunferencia es:
Longitud = π * Diámetro
En este caso, si el diámetro es de 32 cm, podemos calcular la longitud de la siguiente manera:
Longitud = π * 32 cm
El valor de π (pi) es una constante que representa la relación entre la circunferencia de un círculo y su diámetro. Usualmente, se aproxima a 3.14159.
Por lo tanto, la longitud de la circunferencia sería:
Longitud ≈ 3.14159 * 32 cm
Calculando el resultado:
Longitud ≈ 100.53096 cm
Por lo tanto, la longitud de la circunferencia con un diámetro de 32 cm sería aproximadamente 100.53 cm.
Read moe on circumference here https://brainly.com/question/27447563
#SPJ1
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
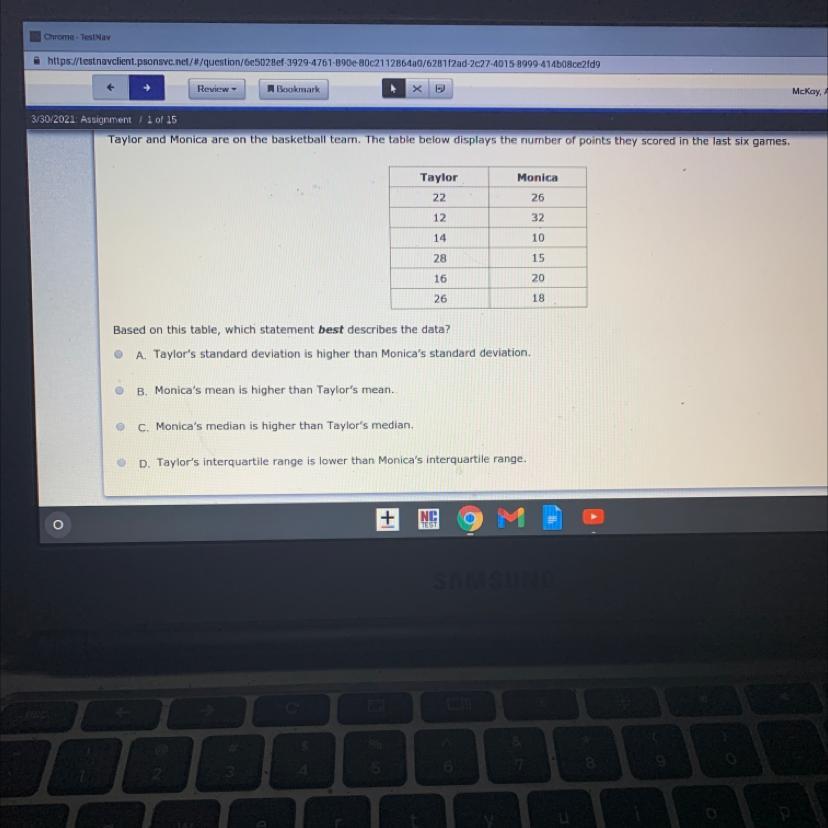
Answers
Answer:
D. TAYLOR'S INTERQUARTILE RANGE IS LOWER THAN MONICA'S INTERQUARTILE RANGE
The mean time required to repair breakdowns of a certain copying machine is 93 minutes. The company which manufactures the machines claims that breakdowns of its newer model are easier to fix. To test this claim, a sample of 18 breakdowns of the new model were observed, resulting in a mean repair time of 86.8 minutes with a standard deviation of 14.6 minutes. Using a significance level of a = 0.10, determine if the new copy machines are faster to repair. State clearly what your null and alternative hypotheses are, show your work, and state your conclusion.
Answers
A significance level of 0.10, we have enough evidence to conclude that the new copy machines have a significantly faster mean repair time compared to the older model.
To test if the new copy machines are faster to repair, we can set up the following null and alternative hypotheses:
Null Hypothesis (H₀): The mean repair time for the new copy machines is the same as the mean repair time for the older model.
Alternative Hypothesis (H₁): The mean repair time for the new copy machines is less than the mean repair time for the older model.
Let's perform a one-sample t-test to test these hypotheses. The test statistic is calculated as:
t = (sample mean - population mean) / (sample standard deviation / √(sample size))
Given:
Population mean (μ) = 93 minutes
Sample mean (\(\bar x\)) = 86.8 minutes
Sample standard deviation (s) = 14.6 minutes
Sample size (n) = 18
Significance level (α) = 0.10
Calculating the test statistic:
t = (86.8 - 93) / (14.6 / sqrt(18))
t = -6.2 / (14.6 / 4.24264)
t ≈ -2.677
The degrees of freedom for this test is n - 1 = 18 - 1 = 17.
Now, we need to determine the critical value for the t-distribution with 17 degrees of freedom and a one-tailed test at a significance level of 0.10. Consulting a t-table or using statistical software, the critical value is approximately -1.333.
Since the test statistic (t = -2.677) is less than the critical value (-1.333), we reject the null hypothesis.
To know more about significance level:
https://brainly.com/question/4599596
#SPJ4
Comparing two algorithms.
Say we have two different algorithms with respective runtimes of f(n) and g(n). Given the following cases, prove whether or not f(n) = ϴ(g(n)) is true in each case. Show your work but with the crucial steps only. P.S. sqrt(n) means the square-root of n, aka n^(½).
Case
f(n)
g(n)
A
log(n^200)
log(n^2)
B
sqrt(n)
log(n)
C
3^n
5^n
D
sin(n)+3
cos(n)+1
Answers
f(n) = ϴ(g(n)) is not true in cases B(sqrt(n)log(n), C(\(3^n 5^n\)), and D(sin(n)+3 cos(n)+1).
A) \(log(n^200) log(n^2)\)
Here, f(n) = \(log(n^200)\) and g(n) = \(log(n^2)\). Now, if we take the limit of f(n) / g(n) as n approaches infinity, then:
f(n) / g(n) = \([log(n^200) / log(n^2)]\) = 100
This means that as n approaches infinity, the ratio f(n) / g(n) is constant, and so we can say that f(n) = ϴ(g(n)). Therefore, f(n) = ϴ(g(n)) is true in this case.
B) sqrt(n) log(n) Here, f(n) = sqrt(n) and g(n) = log(n). Now, if we take the limit of f(n) / g(n) as n approaches infinity, then:
f(n) / g(n) = [sqrt(n) / log(n)]
As log(n) grows much slower than sqrt(n) as n approaches infinity, this limit approaches infinity. Therefore, we cannot say that f(n) = ϴ(g(n)) is true in this case.
C) 3^n 5^n
Here, f(n) = \(3^n\) and g(n) = \(5^n\) . Now, if we take the limit of f(n) / g(n) as n approaches infinity, then:
f(n) / g(n) = \([3^n / 5^n]\)
As \(3^n\) grows much slower than \(5^n\) as n approaches infinity, this limit approaches zero. Therefore, we cannot say that f(n) = ϴ(g(n)) is true in this case.
D) sin(n) + 3 cos(n) + 1
Here, f(n) = sin(n) + 3 and g(n) = cos(n) + 1. Now, if we take the limit of f(n) / g(n) as n approaches infinity, then:
f(n) / g(n) = [sin(n) + 3] / [cos(n) + 1]
As this limit oscillates between positive and negative infinity as n approaches infinity, we cannot say that f(n) = ϴ(g(n)) is true in this case.
Therefore, f(n) = ϴ(g(n)) is not true in cases B, C, and D.
To know more about log refer here:
https://brainly.com/question/32621120
#SPJ11
help please anyone?
giving brainliestt

Answers
Answer:
School Y = 4 points
School X = 12 points
Step-by-step explanation:
school x=school y+8
school x=3 school y
x=y+8
x=3y
3y=y+8
2y=8
y=4
x=12
help need this asap will give brainliest!

Answers
When the sine function sinθ = 0.5126 then the angle θ is 30.001°
Given sinθ = 0.5126
We have to find the value of θ or the angle θ.
We know that the sine function is a ratio of opposite side and hypotenuse.
As given value sinθ = 0.5126
To find θ value, we take sin⁻¹ on both sides of the equation.
sin⁻¹(sinθ)=sin⁻¹(0.5126)
On left side the sine and its inverse will be cancelled and left with angle θ.
Now θ = sin⁻¹(0.5126)
To find the value of sin⁻¹(0.5126), you can use the inverse sine function or arcsin function.
θ = 30.001°
Hence, when the sine function sinθ = 0.5126 then the angle θ is 30.001°
To learn more on trigonometry click:
https://brainly.com/question/25122835
#SPJ1
tripling the linear size of an object multiplies its area by
Answers
Tripling the linear size of an object multiplies its area by a factor of nine.
When the linear size of an object is tripled, the area of the object is multiplied by 9.
This can be understood by considering the relationship between the linear size and the area of an object. If we assume that the object has a regular shape and the linear size refers to the length of its sides, then the area is directly proportional to the square of the linear size.
Let's denote the initial linear size of the object as L and the initial area as A. When the linear size is tripled, it becomes 3L. According to the square proportionality, the new area (A') can be expressed as:
A' = (3L)^2
A' = 9L^2
Comparing A' with the initial area A, we can see that A' is 9 times larger than A. Therefore, tripling the linear size of an object multiplies its area by 9.
for such more question on linear size
https://brainly.com/question/19803308
#SPJ8
for an experiment comparing more than two treatment conditions, why should you use analysis of variance rather than separate t tests? group of answer choices
Answers
Using ANOVA rather than separate t-tests is generally recommended when comparing more than two treatment conditions because it provides greater statistical power, helps control for experiment-wise error rate, and can identify interactions between treatments.
What is a t-test?
A t-test is a statistical hypothesis test used to determine whether there is a significant difference between the means of two groups or samples. It is a parametric test that assumes the data is normally distributed and that the variances of the two groups are equal.
When comparing more than two treatment conditions, it's generally recommended to use analysis of variance (ANOVA) rather than separate t-tests for several reasons:
Reduced Type I error: When conducting multiple t-tests, the risk of Type I error (rejecting the null hypothesis when it's actually true) increases with each additional test conducted. ANOVA helps to reduce this risk by testing all treatments simultaneously, rather than testing each treatment separately.
Increased power: ANOVA is more powerful than t-tests when there are multiple treatment conditions because it uses all the available data to estimate treatment effects. This can help to identify differences between groups that may not be significant when comparing only two groups at a time.
Ability to detect interactions: ANOVA can also identify interactions between treatments, which t-tests cannot do. This is important because it allows you to test whether the effect of one treatment depends on the level of another treatment, which may be of interest in many experimental contexts.
Better control over experiment-wise error rate: ANOVA allows for better control over the overall error rate, meaning that it's easier to maintain a desired level of significance across all comparisons. In contrast, conducting multiple t-tests can result in an increased risk of committing at least one Type I error.
Hence, using ANOVA rather than separate t-tests is generally recommended when comparing more than two treatment conditions because it provides greater statistical power, helps control for experiment-wise error rate, and can identify interactions between treatments.
To learn more about the t-test visit:
https://brainly.com/question/17438355
#SPJ4
A bowling alley charges $15 per game. Customers are also charged an additional $3 to rent bowling shoes.
Which statement is true, based on the given description?
A) The description shows a linear relationship, but not a proportional relationship.
B) The description shows a linear relationship and a proportional relationship.
C) The description does not show a linear relationship or a proportional relationship.
D) The description shows a proportional relationship, but not a linear relationship.
Answers
The description indicates a linear relationship, not a proportional one, so option A is accurate.
Explain equation?Two equations are considered to be comparable when their roots and solutions line up. To create an equivalent equation, the identical quantity, symbol, or expression must be either added to or removed from both of the equation's two sides. We can also create a similar equation by dividing or multiplying the two sides of the equation by an nonzero value.
A) The relationship is described as linear rather than proportional.
The cost of bowling can be represented by the equation C = 15 + 3x, where C is the total cost, and x is the number of games played. This is a linear relationship because the cost increases at a constant rate as the number of games played increases.
However, this is not a proportional relationship because the additional cost of $3 for renting shoes does not stay the same for every game played. It is a fixed fee that is added to the cost of each game. If the cost of shoes was proportional to the number of games played, then the cost per game would stay the same regardless of how many games were played.
To know more about equation visit:
https://brainly.com/question/2972832
#SPJ1
X^2 - 2x + 6 = 0
Show all work
Answers
Answer:
x= plus or minus 1 plus imaginary root times square root of 5.
Step-by-step explanation:
\( {x}^{2} - 2x + 6 = 0\)
Complete the Square.
\( {x}^{2} - 2x = - 6\)
\( {x}^{2} - 2x + 1 = - 5\)
\((x - 1) {}^{2} = - 5\)
\(x = + - 1 + i \sqrt{5} \)