1. The total cost in dollars to buy uniforms for the players on a volleyball team can be
found using the function c = 34.95u + 6.25, where u is the number of uniforms
bought. If there are at least 8 players but not more than 12 players on the volleyball
team, what is the domain of the function for this situation?
Answers
The domain will be the integer numbers between 8 and 12 using the limits in other words 8 ≤ u ≤ 12
this is considering every player will bought only one uniform for the season
Hope this helped!
if thats not it read this and see if this works out
The domain of the function is
Step-by-step explanation:
Given : The total cost in dollars to buy uniforms for the players on a volleyball team can be found using the function c= 34.95u +6.25, where u is the number of uniforms bought.
If there are at least 8 players but not more than 12 players on the volleyball team.
To find : What is the domain of the function for this situation ?
Solution :
The total cost in dollars c= 34.95u +6.25
Where, u is the number of uniforms bought.
Now, The number of uniforms bought depend on the number of players.
We have given that, there are at least 8 players but not more than 12 players on the volleyball team.
i.e, The number of players are between 8 to 12.
So, The domain of the function is
8< u < 12
hope this helped
Related Questions
17.A company produces three sizes of a dog
25 house: small, medium, and large. The
small dog house sells for $80, the
medium size for $110, and the large for
$140. The small dog houses cost $50
each to make, medium $70 each, and
large $79 each. Let s represent the
number of small size dog houses, m
represent the number of medium size
dog houses and L represent the number
of large size dog houses. Write an
expression in simplest form for the net
profit.
Answers
Answer:
10s+40m+61l=net profit
Step-by-step explanation:
subtract the value you pay from the value you charge
Obtain numerical solution of the ordinary differential equation y' = 3t−10y²
with the initial condition: y(0)= −2 by Euler method using h=0.5 Perform 3 steps.
Solution of all problems MUST contain general formula and all intermediate results. Perform numerical computations using 4 digits after decimal point.
Answers
The Euler method with a step size of h = 0.5, the approximate numerical solution for the ODE is y(1.5) ≈ -1.1198 x 10^9.
To solve the ODE using the Euler method, we divide the interval into smaller steps and approximate the derivative with a difference quotient. Given that the step size is h = 0.5, we will perform three steps to obtain the numerical solution.
we calculate the initial condition: y(0) = -2.
1. we evaluate the derivative at t = 0 and y = -2:
y' = 3(0) - 10(-2)² = -40
Next, we update the values using the Euler method:
t₁ = 0 + 0.5 = 0.5
y₁ = -2 + (-40) * 0.5 = -22
2. y' = 3(0.5) - 10(-22)² = -14,860
Updating the values:
t₂ = 0.5 + 0.5 = 1
y₂ = -22 + (-14,860) * 0.5 = -7492
3. y' = 3(1) - 10(-7492)² ≈ -2.2395 x 10^9
Updating the values:
t₃ = 1 + 0.5 = 1.5
y₃ = -7492 + (-2.2395 x 10^9) * 0.5 = -1.1198 x 10^9
Therefore, after performing three steps of the Euler method with a step size of h = 0.5, the approximate numerical solution for the ODE is y(1.5) ≈ -1.1198 x 10^9.
Learn more about Euler method here:
https://brainly.com/question/30459924
#SPJ11
Find X ( please explain how)
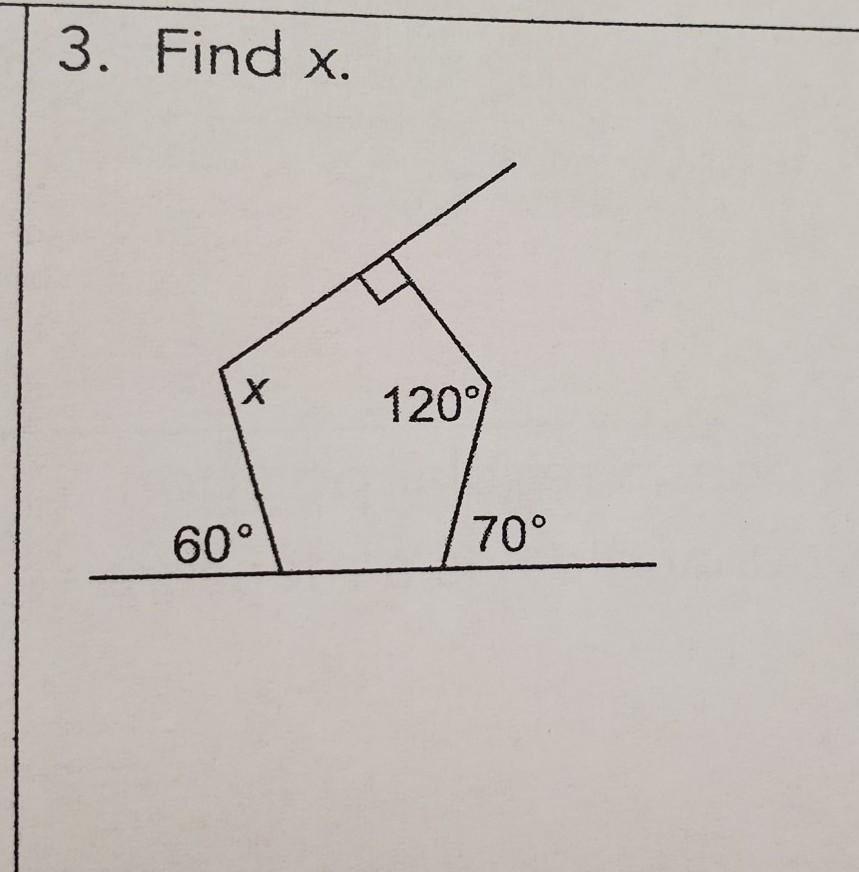
Answers
Answer:
90
Step-by-step explanation:
(5-2)x180= 540 formula to find the sum of interior angles of a polygon
180-70 = 110 lower right angle
180 -60 = 130 lower left angle
110+130+120+90= 450 all known angles sum
540-450 = 90 total minus known gives you x
the standard deviation is the square root of the variance T/F
Answers
The statement "the standard deviation is the square root of the variance" is TRUE.What is the standard deviation?The standard deviation is a statistical measure that calculates the amount of variability or dispersion in a set of data.
It quantifies the distribution's spread by measuring the average distance of each point from the mean. In other words, it's a measure of how much the values in a data set deviate from the mean.What is the variance?Variance is a statistical measure that quantifies the distribution's dispersion.
It is defined as the average of the squared distances of each data point from the mean of the data set. It provides information on how spread out the data is with regard to the mean.Standard Deviation vs VarianceThe variance and standard deviation are two closely related statistical measures.
The variance is computed by squaring the standard deviation. To calculate the standard deviation, take the square root of the variance. In simpler terms, the standard deviation is the square root of the variance.Therefore, the statement "the standard deviation is the square root of the variance" is TRUE.
To learn more about standard deviation, visit
brainly.com/question/475676
#SPJ11
Find each percent change. Round to nearest percent. State if it is a increase or a decrease.

Answers
Percent change = change in value/original value.
13) 75 -> 38: 37 decrease/75 original
49.3333333333333% decrease
about 49% decreaase
14) 97 -> 3: 94 decreace/97 original
96.9072164948454% decrease
about 97% decrease
15) 77 -> 55: 22 decrease/77 original
28.5714285714286% decrease
about 29% decrease
16) 67 -> 28: 39 decrease/67 original
58.2089552238806% decrease
about 58% decrease
the length of a rectangular piece of sheet metal is longer than its width. a square piece that measures on each side is cut from each corner, then the sides are turned up to make a box with volume . find the length and width of the original piece of sheet metal.
Answers
The width of the original piece of sheet metal is (w^2 - l^2)/(3w + 3l), and the length is (l^2 - w^2)/(3w + 3l).
To solve this problem, we can use the formula for the volume of a rectangular box, which is V = lwh, where l is the length, w is the width, and h is the height.
First, let's find the height of the box. Since we cut squares from each corner, the height of the box is the length of the square that was cut out. Let's call this length x.
The width of the box is the original width minus the lengths of the two squares that were cut out, which is w - 2x.
Similarly, the length of the box is the original length minus the lengths of the two squares that were cut out, which is l - 2x.
Now we can write the volume of the box in terms of x, w, and l:
V = (w - 2x)(l - 2x)(x)
Expanding this expression, we get:
V = x(4wl - 4wx - 4lx + 8x^2)
Simplifying further:
V = 4x^3 - 4wx^2 - 4lx^2 + 4wlx
To find the dimensions of the original piece of sheet metal, we need to maximize this volume. We can do this by taking the derivative of the volume with respect to x and setting it equal to zero:
dV/dx = 12x^2 - 8wx - 8lx + 4wl = 0
Solving for x, we get:
x = (2wl)/(3w + 3l)
Now we can use this value of x to find the width and length of the original piece of sheet metal:
w - 2x = w - 2(2wl)/(3w + 3l) = (w^2 - l^2)/(3w + 3l)
l - 2x = l - 2(2wl)/(3w + 3l) = (l^2 - w^2)/(3w + 3l)
Know more about volume of a rectangle here:
https://brainly.com/question/21308574
#SPJ11
If y varies directly with x find the value of y when k = 4 and x =2
Answers
If y varies directly with x then value of y is 8 when k = 4 and x =2
When y is directly varies with x the equation is y=kx
We have to find the value of y when k is four and x is two
k=4 and x=2
Plug in these values in equation
y=4×2
Value of y is four times two
y=8
Hence, If y varies directly with x then value of y is 8 when k = 4 and x =2
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Jaime has a board that is 8 feet long. He cuts the board into three equal pieces. How long is each piece.
SHOW WORK PRETTY PLEASE WITH SUGARCANE JUICE!!!
Answers
Each piece is 2 ft and 8 inches long.
Explanation:
12 inches are in a foot, so 12 times 8 equals 96.You then divide 96 by 3 which is 32.So 32 inches is 12in+12in+8in= 2feet 8 inches
how many cup dose it take

Answers
Answer:
4 gallons = 64 cups
1 gallons = 16 cups
3 gallons = 48 cups
Jan says that a rhombus is a parallelogram and that every parallelogram is also a rhombus. Is Jan correct?
Part 2***
Explain why or why not.
Answers
Answer:
No
Step-by-step explanation:
Not all parallelograms are rhombuses, some parallelograms include rectangles, squares, hexagons, etc.
No. Jan is not correct. So, all parallelograms are not rhombuses.
What is a rhombus?A rhombus is a parallelogram because the opposite sides are parallel but every parallelogram is not a rhombus because all sides may not be equal. Every square is a rectangle because opposite sides are equal but not every rectangle is a square because all sides might not be equal. Every square is rhombus because all sides are equal but not every rhombus is a square because the angles might not be right angles.
here, we have,
We need to identify the properties of the given figure in order to answer why one figure can not be the other one:
A rhombus has all sides equal as well as parallel but all angles might not be right angles.
A square has all four sides equal and has 4 right angles.
A rectangle has equal opposite sides and 4 right angles.
A parallelogram has opposite parallel sides.
Hence, a rhombus can be a parallelogram because the opposite sides are parallel but every parallelogram can not be a rhombus because all sides may not be equal. Every square is a rectangle because opposite sides are equal but not every rectangle is a square because all sides might not be equal. Every square is rhombus because all sides are equal but not every rhombus is a square because the angles might not be right angles.
A parallelogram has opposite sides parallel and equal in length. Also, opposite angles are equal. Squares, rectangles, and rhombuses are all parallelograms. So all parallelograms are not rhombuses.
Not all parallelograms are rhombuses, some parallelograms include rectangles, squares, hexagons, etc.
To know more about rhombus here
brainly.com/question/12665650
#SPJ3
A 13 foot long ladder leans against a house. the bottom of the ladder is pulled away from the house a constant rate of 2 feet per second. a. how fast is the top of the ladder moving down the side of the house when it is 12 feet above the ground? b. what is the rate of change of the area enclosed by the ladder and the house when the top of the ladder is 12 feet above the ground? c. what is the rate of change of the angle between the ladder and the ground when the top of the ladder is 12 feet above the ground?
Answers
a. The top of the ladder is moving down at 5/12 ft/s.
b. The area enclosed is changing at -25/24 sq ft/s.
c. The angle is changing at approximately -0.347 radians per second.
a. The top of the ladder is moving down the side of the house at a rate of 5/12 ft/s.
Using the Pythagorean theorem, differentiate
\(x^2 + y^2 = 13^2. At y = 12, x = √(13^2 - 12^2) = 5.\)
Solve for dy/dt to get -5/12 ft/s.
b. The rate of change of the enclosed area is 24/5 sq ft/s.
Differentiate the area formula
\(A = (1/2)xy. At y = 12, x = 5.\)
Substitute these values and differentiate with respect to time to get \(dA/dt = (1/2)(5)(-5/12) = -25/24 sq ft/s.\)
c. The rate of change of the angle is approximately -0.347 radians per second.
Use trigonometry to
\(find θ = arctan(y/x). At y = 12, x = 5, so θ ≈ arctan(12/5) ≈ 1.176\) radians. Differentiate with respect to time to find dθ/dt = -5/144π radians/s.
learn more about Pythagorean here:
https://brainly.com/question/28032950
#SPJ11
In a breadth-first traversal of a graph, what type of collection is used in the generic algorithm? queue Ostack set Oheap
Answers
In a breadth-first traversal of a graph, a queue is typically used as the collection in the generic algorithm.
Breadth-first traversal is an algorithm used to visit all the vertices of a graph in a breadth-first manner, exploring all the neighbors of a vertex before moving on to the next level of vertices. To implement this algorithm, a queue data structure is commonly used. A queue follows the First-In-First-Out (FIFO) principle, meaning that the element that has been in the queue for the longest time is the first one to be removed. In the context of a breadth-first traversal, the queue is used to hold the vertices that have been discovered but not yet explored. As the traversal progresses, vertices are added to the queue and then processed in the order they were added, ensuring that vertices at the same level are explored before moving to the next level. The queue data structure provides the necessary functionality for adding elements to the back and removing elements from the front efficiently, making it suitable for the breadth-first traversal algorithm.
Learn more about Breadth-first traversal here:
https://brainly.com/question/31953449
#SPJ11
- Evaluate Sc (y + x – 4ix3)dz where c is represented by: C:The straight line from Z = 0 to Z = 1+ i C2: Along the imiginary axis from Z = 0 to Z = i. = =
Answers
The value of the integral C1 and C2 are below:
∫[C1] (y + x – 4ix³) dz = -1/2 + 4/3 i
∫[C2] (y + x – 4ix³) dz = 0
To evaluate the integral, we need to parameterize the given contour C and express it as a function of a single variable. Then we substitute the parameterization into the integrand and evaluate the integral with respect to the parameter.
Let's evaluate the integral along contour C1: the straight line from Z = 0 to Z = 1 + i.
Parameterizing C1:
Let's denote the parameter t, where 0 ≤ t ≤ 1.
We can express the contour C1 as a function of t using the equation of a line:
Z(t) = (1 - t) ×0 + t× (1 + i)
= t + ti, where 0 ≤ t ≤ 1
Now, we'll calculate the differential dz/dt:
dz/dt = 1 + i
Substituting these into the integral:
∫[C1] (y + x – 4ix³) dz = ∫[0 to 1] (Im(Z) + Re(Z) - 4i(Re(Z))³)(dz/dt) dt
= ∫[0 to 1] (t + 0 - 4i(0)³)(1 + i) dt
= ∫[0 to 1] (t + 0)(1 + i) dt
= ∫[0 to 1] (t + ti)(1 + i) dt
= ∫[0 to 1] (t + ti - t + ti²) dt
= ∫[0 to 1] (2ti - t + ti²) dt
= ∫[0 to 1] (-t + 2ti + ti²) dt
Now, let's integrate each term:
∫[0 to 1] -t dt = [-t²/2] [0 to 1] = -1/2
∫[0 to 1] 2ti dt = \(t^{2i}\)[0 to 1] = i
∫[0 to 1] ti² dt = (1/3)\(t^{3i}\) [0 to 1] = (1/3)i
Adding the results together:
∫[C1] (y + x – 4ix³) dz = -1/2 + i + (1/3)i = -1/2 + 4/3 i
Therefore, the value of the integral along contour C1 is -1/2 + 4/3 i.
Let's now evaluate the integral along contour C2: along the imaginary axis from Z = 0 to Z = i.
Parameterizing C2:
Let's denote the parameter t, where 0 ≤ t ≤ 1.
We can express the contour C2 as a function of t using the equation of a line:
Z(t) = (1 - t)× 0 + t × i
= ti, where 0 ≤ t ≤ 1
Now, we'll calculate the differential dz/dt:
dz/dt = i
Substituting these into the integral:
∫[C2] (y + x – 4ix³) dz = ∫[0 to 1] (Im(Z) + Re(Z) - 4i(Re(Z))³)(dz/dt) dt
= ∫[0 to 1] (0 + 0 - 4i(0)³)(i) dt
= ∫[0 to 1] (0)(i) dt
= ∫[0 to 1] 0 dt
= 0
Therefore, the value of the integral along contour C2 is 0.
In summary:
∫[C1] (y + x – 4ix³) dz = -1/2 + 4/3 i
∫[C2] (y + x – 4ix³) dz = 0
Learn more about integral here:
https://brainly.com/question/31059545
#SPJ11
Consider the initial value problem y' = 3y^2, y(0) = y0. What value(s) of y0| will the solution have a vertical asymptote at t = 2 and a thinterval of existence - [infinity]
Answers
Consider the initial value problem y' = 3y^2, at the value of y(0) = 1/6 will the solution have a vertical asymptote at t = 2.
The differential equation is y'=3y^2.
We can write this equation as:
dy/dt = 3y^2
dy/y^2 = 3dt
Now integrating on both side
\(\int \frac{dy}{y^2} = \int 3dt\)
After integrating we get,
- 1/y = 3t + c
Multiply by y on both side, we get
(3t + c)y = -1
Divide by (3t + c) on both side, we get
y = -1/(3t + c).................(1)
Since there is vertical asymptote at t = 2
So 3t + c = 0 at t = 2
3(2) + c = 0
6 + c = 0
Subtract 6 on both side, we get
c = -6
Put the value of c in equation 1
y = -1/(3t - 6)
At t = 0
y(0) = -1/(3(0) - 6)
y(0) = 1/6
To learn more about vertical asymptote link is here
brainly.com/question/4084552
#SPJ4
Brandon is hiking a trail that leads to the top of a canyon. The trail is 4.2 miles long, and Brandon plans to stop for Lunch after he completes 1.6 miles. What expression represents the remaining distance Brandon needs to hike?
Answers
Answer: See explanation
Step-by-step explanation:
From the question, we are informed that the trail that Brandon is hiking is 4.2 miles long, and Brandon plans to stop for Lunch after he completes 1.6 miles.
The expression represents the remaining distance Brandon needs to hike will be gotten by subtracting 1.6 miles from 4.2 miles. This will be:
= 4.2 - 1.6
= 2.6 miles
Complete the steps in order to write the inverse of f(x)=x+5
=x45
1.
Writing the Inverse of a Function
2.
3,
1-x-5
Answers
The equation of the inverse function of the function f(x) = x + 5 is f'1(x) = x - 5
What are inverse functions?Inverse functions are the opposite of an original equation. This means that for a function f(x), the inverse of the function f(x) is f-(x); it also represents the opposite function
How to determine the inverse functions?The function f(x) is given as
f(x) = x + 5
As a general rule, we start by writing f(x) as a variable (say f(x) = y).
So, the equation of the function becomes
y = x + 5
The next step is to switch/swap the positions of x and y in the above equation y = x + 5
The equation becomes
x = y + 5
The next step is to make y the subject of the formula in the above equation x = y + 5
The equation becomes
y = x - 5
This is done by subtracting 5 from both sides of the equation.
So, we have:
y = x - 5
Express as an inverse function
f'1(x) = x - 5
Hence, the inverse function of the function f(x) = x + 5 is f'1(x) = x - 5
Read more about inverse equations at:
brainly.com/question/14391067
#SPJ1
Please help me!! I’ll mark you beainliest

Answers
Answer:
11 months
Step-by-step explanation:
50m + 75 >= 600
just solve the inequality like how you would solve an equation, by inverse operations and simplifying
50m + 75 >= 600
-75 -75
50m >= 525
/50 /50
m>= 10.5
just round up, because 0.5 of a month really isn't an answer
so 11 months
when sampling from a population with , which of the following sample means is more surprising? why? sample a: a random sample of 9 pell grant recipients with a mean award amount of $2750. sample b: a random sample of 36 pell grant recipients with a mean award amount of $2750.
Answers
Sample mean in sample b to be less variable and more representative of population mean than sample mean in sample a.
Standard error measures the variability of sample means around the population mean.
It decreases as sample size increases.
Using the formula for the standard error of the mean,
Calculate the standard errors for each sample,
Standard error of sample a
= s/√(n)
= 850/√(9)
= 283.33
Standard error of sample b
= s/√(n)
= 850/√(36)
= 141.67
Where s is the sample standard deviation
And n is the sample size.
The standard error of sample b is smaller than the standard error of sample a.
Sample mean in sample b is more likely to be closer to true population mean than sample mean in sample a.
Therefore, sample mean b is more surprising as larger sample size makes it more likely and accurately represents population mean.
learn more about sample mean here
brainly.com/question/14727460
#SPJ4
Complete the table of values for f(x) = -3|x+1|-4 using the table of values for g(x) = |x|
Answers
f(x)>=-7
Functions:
Function, in mathematics, is an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable). Functions are ubiquitous in mathematics.
If a variable y is so related to a variable x that whenever a numerical value is assigned to x, there is a rule according to which a unique value of f(x)is determined, then f(x) is said to be a function of the independent variable x
Given :
f(x) = -3|x+1|-4
using the table of values for g(x) = |x|
Solution :
f(x) = -3|x+1|-4
f(x) = -3|g(x)+1|-4
f(x) = -3||x|+1|-4
which means |x| is always positive |x|>0
f(x) = -3||x|+1|-4
f(x) = -3x-3-4
f(x) = -3x-7
f(x)>=-7
For more details: brainly.com/question/18071485
#SPJ9
The sides of a rectangle are 6.3 cm and 4.8cm, each correct to 1 decimal place.
Calculate the upper bound for the area of the rectangle.
Answers
Answer:
error= 0.1/2, 0.05
4.8 + 0.05 = 4.85
6.3 + 0.05 = 6.35
4.85 x 6.35 = 30.7975 cm (when rounded, gives 30.80 cm).
Step-by-step explanation:
Which two numbers are equivalent in value?

Answers
Answer:
Step-by-step explanation:
its b
Find the area of the yellow region.
Round to the nearest tenth.
6 in
6 in-
Area = [?] in²
Answers
We can see here that the area of the yellow region will be 3.9 in² (nearest tenth).
What is area?The term "area" refers to a specific extent or region of space. It is a measurement of the two-dimensional space within a defined boundary.
We see a square of 6 inch in side, divided in two semi-circles.
Radius of semi-circle = 3 inch
Area of square = 6 × 6 = 36 in²
Area of semi-circle = π/(r)² = 22/(2 ×7)(3)² = 14.14 in²
Area of two semi-circles = 14.14 + 14.14 = 28.28in²
Thus, area of yellow region = (36 - 28.28)/2 3.86 in²
Learn more about area on https://brainly.com/question/2607596
#SPJ1
![Find the area of the yellow region.Round to the nearest tenth.6 in6 in-Area = [?] in](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/Sd3Yt9e7QL008y3HdtJIEgupnJSjBZDj.jpeg)
select a pair of numbers that have a sum of 9 and a difference of 1
Answers
Answer:
The two numbers with the sum of 9 and difference of 1 is 5 and 4.
Step-by-step explanation:
Answer:
The answer is 4 and 5.
Step-by-step explanation:
4+5 = 9
5-4 = 1
MARK ME BRAINLIEST!!
Find the GCF of the monomials: 18x² and 21x²y
A)3x
B)3x²
C)3xy
D)3x²y
PLEASE HELP MEEE
Answers
exercise 3.3.2: Unions and intersections of sequences of sets. i About Use the definition for Aj to answer the questions. Forie Z+, A; is the set of all positive integer multiples of i. (a) Describe the following set using set builder notation: 5 n Ai i=1 (b) Describe the following set using roster notation: (Ů4) Ai ) n{Z:1 < x < 20}
Answers
For part (a), we are asked to describe the set {5} ∪ {10} ∪ {15} ∪ {20} ∪ {25} using set builder notation, where each set is Ai = {ix : i ∈ Z+}.
To do this, we can simply list out all the elements of the set and use set builder notation to describe it. The set contains the elements {5, 10, 15, 20, 25}, so we can describe it as:
{ix : i ∈ Z+ and i = 1, 2, 3, 4, or 5}
Alternatively, we could also use interval notation to describe the set:
{ix : i ∈ Z+ and i ∈ [1, 5]}
For part (b), we are asked to describe the set (Ů4) Ai ∩ {x : 1 < x < 20} using roster notation, where each set is Ai = {ix : i ∈ Z+}.
To do this, we first need to find the union of the first 4 sets, which is given by:
{1, 2, 3, 4, 5} ∪ {2, 4, 6, 8, 10} ∪ {3, 6, 9, 12, 15} ∪ {4, 8, 12, 16, 20}
We can then take the intersection of this set with the set {x : 1 < x < 20}, which gives us the elements {2, 3, 4, 6, 8, 12, 16}, so we can describe the set using roster notation as:
{2, 3, 4, 6, 8, 12, 16}
Hi! I'm happy to help you with Exercise 3.3.2 regarding unions and intersections of sequences of sets.
(a) Using set builder notation, you can describe the set 5 ∪ Ai (i=1) as:
{ x ∈ Z+ : x is a positive integer multiple of any i where 1 ≤ i ≤ 5 }
(b) To describe the set (∪4 Ai) ∩ {Z: 1 < x < 20} using roster notation, first list the elements of each Ai for i = 1 to 4, and then find the elements that are also in the set {Z: 1 < x < 20}.
A1: {2, 4, 6, 8, 10, 12, 14, 16, 18}
A2: {3, 6, 9, 12, 15, 18}
A3: {4, 8, 12, 16}
A4: {5, 10, 15, 20}
Now, find the union of these sets:
∪4 Ai = {2, 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20}
Finally, find the intersection with the set {Z: 1 < x < 20}:
(∪4 Ai) ∩ {Z: 1 < x < 20} = {2, 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 16, 18}
So the roster notation for this set is:
{2, 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 16, 18}
To learn more about notation visit;
brainly.com/question/29531272
#SPJ11
the yellow cab company charges a flat fee of $3.50 and an additional $2.50 per mile. the relaxicab company charge $2.30 per mile and a $4.54 fee. at how many miles do the two companies charege the same amount? write a system of equations that computes the cost of the cabs. use for the miles, and for the cost.
Answers
Step-by-step explanation:
Since the initial fee is fixed, we can assume it is a constant and the succeeding mile fee is the variable as it changes for every mile covered.
Let x = distance (mile)
let y = total charge (dollars)
Yellowcab company equation for cost calculation; 3.50 + 2.5x = y
laxicab company equation for cost calculation; 4.54+2.3x = z
the two companies charge the same amount when y = z
; 3.50 + 2.5x = 4.54+2.3x
x = 5.2 miles
COST CALCULATION
;3.50 + 2.5x = ?
if x = 5.2;
; 3.50 + 2.5(5.2) =$16.50
OR
; 4.54+2.3x = ?
; 4.54 + 2.3(5.2) = $16.50
Solve the triangle a=38 b=31 and c=35. find
a.
a=43, b=47,c=90
b.
a=50, b=70 c=59.9
c.
a=70, b50.1, c=59.9
d.
a=60, b=70, c=50
Answers
A = 70.005 rounding to 70
B = 50.05, rounding to 50.1
C = 59.94 leaving it at 59.9 !
This graph represents the path of a baseball hit during practice.
What does the y-value of the vertex represent?
A. The maximum height of the baseball
B. The time the baseball reaches it’s maximum height
C. The time the baseball was hit
D. Ground level
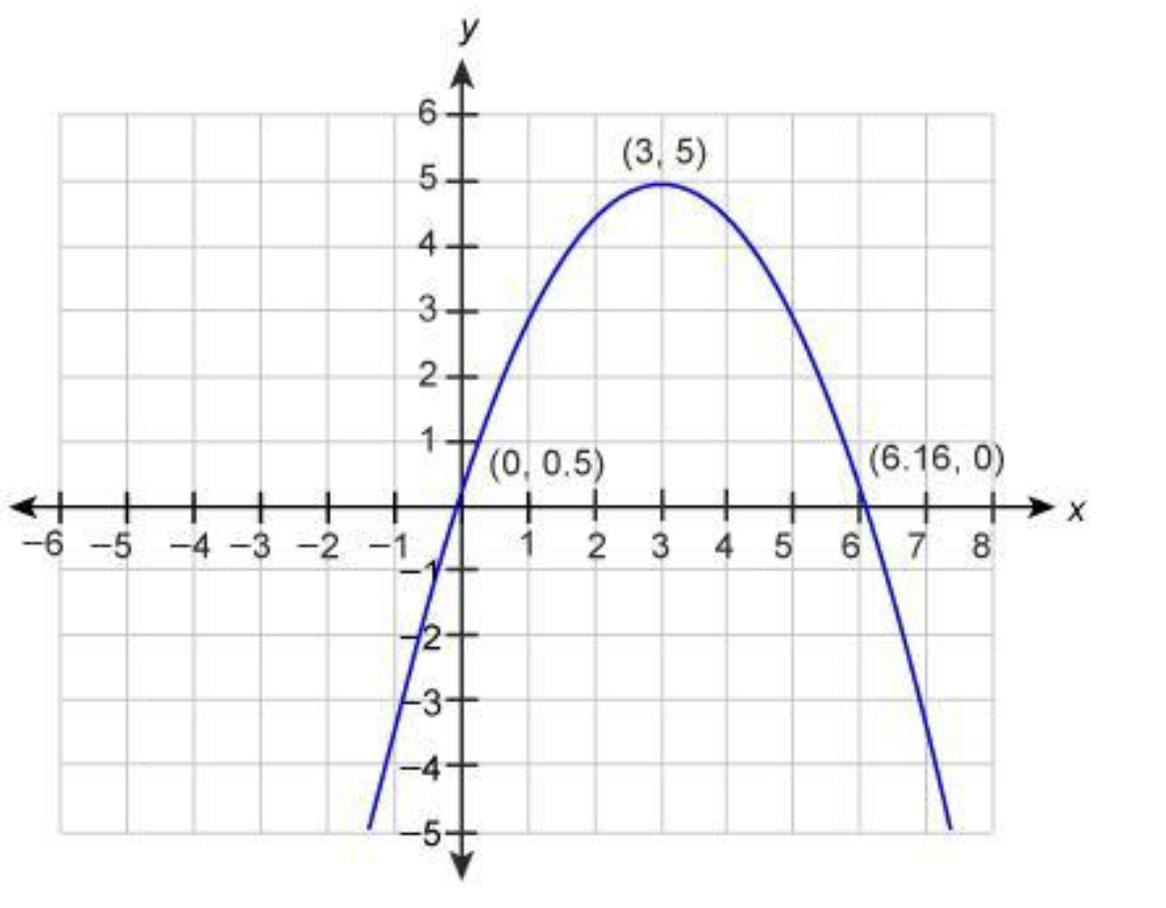
Answers
Answer:
the correct answer is A
Step-by-step explanation:
i put B because thats what the first user said it was and i got it wrong on my quiz, the quiz shows the corret answer is A
when julia is writing a first draft, there is 0.7 0.70, point, 7 probability that there will be no spelling mistakes on a page. one day, julia writes a first draft that is 4 44 pages long. assuming that julia is equally likely to have a spelling mistake on each of the 4 44 pages, what is the probability that she will have no spelling mistakes on at least one of them?
Answers
The probability that Julia will have no spelling mistakes on a single page is 0.7. Since Julia is equally likely to have a spelling mistake on each page of her 44-page draft, we need to find the probability that she will have no spelling mistakes on at least one of the pages.
To calculate this probability, we can find the complement, which is the probability of having at least one spelling mistake on any page. The complement can be calculated by subtracting the probability of having no spelling mistakes on any page from 1.
The probability of having no spelling mistakes on any page is (0.7)^44 since each page has an independent probability of 0.7 of having no spelling mistakes.
Therefore, the probability of having at least one spelling mistake on any page is 1 - (0.7)^44.
By substituting the values, we find that the probability of Julia having no spelling mistakes on at least one of the 44 pages is approximately 0.999999999999999999999999998. This means that it is highly unlikely for Julia to have no spelling mistakes on any of the pages, given the probability of no mistakes on a single page.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
A letter is drawn 1,000 times, at random, from the word ARABIA. There are two offers.
A) You win a dollar if the number of A's among the draws is 10 or more above the expected number.
B) You win a dollar if the number of B's among the draws is 10 or more above the expected number.
Choose one option and explain.
(i) A gives a better chance of winning than B.
(ii) A and B give the same chance of winning.
(iii) B gives better chance of winning than A.
(iv) There is not enough information to decide.
Answers
To determine which option gives a better chance of winning, we need to calculate the expected number of A's and B's in the 1,000 draws and compare it to the conditions for winning in each option.
Let's calculate the expected number of A's and B's:
Number of A's in "ARABIA": 3
Number of B's in "ARABIA": 1
Total number of letters in "ARABIA": 6
Probability of drawing an A: 3/6 = 1/2
Probability of drawing a B: 1/6
Expected number of A's in 1,000 draws: (1/2) * 1,000 = 500
Expected number of B's in 1,000 draws: (1/6) * 1,000 = 166.67
Now let's analyze the conditions for winning in each option:
Option A: You win a dollar if the number of A's among the draws is 10 or more above the expected number (500 + 10 = 510 or more).
Option B: You win a dollar if the number of B's among the draws is 10 or more above the expected number (166.67 + 10 = 176.67 or more).
Comparing the two options:
Option A requires having 510 or more A's out of the 1,000 draws.
Option B requires having 176.67 or more B's out of the 1,000 draws.
Since it is not possible to have a fraction of a letter, the number of B's will always be an integer. Therefore, it is impossible to reach the condition for winning in option B, as there can't be 176.67 B's.
Therefore, the correct answer is:
(i) Option A gives a better chance of winning than option B.
Learn more about expected number from
https://brainly.com/question/24305645
#SPJ11