-10+3m+5 can someone please help me do two step equations
Answers
Answer:
3m-5
Step-by-step explanation:
combine like terms
Related Questions
Mark bought gifts for his friends, and each gift cost $9. Let y represent the total cost and represent the number of gifts. Write an equation to represent the proportional relationship between the total cost and the number of gifts he bought. (4 points) Oy=8x a 1 y = 8 x Oy=9x O 1 y = 9 x
Answers
Answer:
y=9x (O 1)
Step-by-step explanation:
9 times the number of gifts he bought which lets say is x will equal your answer (y).
Mary is buying tickets for a movie.
• Each adult ticket costs $9.
• Each child ticket costs $5.
• Mary spends $110 on tickets.
Mary buys 14 total tickets.
Enter the total number of adult tickets and total number of child tickets she buys.
Answers
Answer:
She buys 9 adult tickets and 4
Step-by-step explanation:
tanx(1+cos2x)=sin2x prove the identity
Answers
Using double angle identity, we are able to prove tan(x)(1 + cos(2x)) = sin(2x).
What is the prove of the given identity?To prove the identity tan(x)(1 + cos(2x)) = sin(2x), we can start by using trigonometric identities to simplify both sides of the equation.
Starting with the left-hand side (LHS):
tan(x)(1 + cos(2x))
We know that tan(x) = sin(x) / cos(x) and that cos(2x) = cos²(x) - sin²(x). Substituting these values, we get:
LHS = (sin(x) / cos(x))(1 + cos²(x) - sin²(x))
Next, we can simplify the expression by expanding and combining like terms:
LHS = sin(x) / cos(x) + sin(x)cos²(x) / cos(x) - sin³(x) / cos(x)
Simplifying further:
LHS = sin(x) / cos(x) + sin(x)cos(x) - sin³(x) / cos(x)
Now, let's work on the right-hand side (RHS):
sin(2x)
Using the double angle identity for sine, sin(2x) = 2sin(x)cos(x).
Now, let's compare the LHS and RHS expressions:
LHS = sin(x) / cos(x) + sin(x)cos(x) - sin³(x) / cos(x)
RHS = 2sin(x)cos(x)
To prove the identity, we need to show that the LHS expression is equal to the RHS expression. We can combine the terms on the LHS to get a common denominator:
LHS = [sin(x) - sin³(x) + sin(x)cos²(x)] / cos(x)
Now, using the identity sin²(x) = 1 - cos²(x), we can rewrite the numerator:
LHS = [sin(x) - sin³(x) + sin(x)(1 - sin²(x))] / cos(x)
= [sin(x) - sin³(x) + sin(x) - sin³(x)] / cos(x)
= 2sin(x) - 2sin³(x) / cos(x)
Now, using the identity 2sin(x) = sin(2x), we can simplify further:
LHS = sin(2x) - 2sin³(x) / cos(x)
Comparing this with the RHS expression, we see that LHS = RHS, proving the identity.
Learn more on trigonometric identity here;
https://brainly.com/question/24496175
#SPJ1
Maysol made 75 bracelets this month.
Last month she made 40 bracelets.
What is the percent of change
Answers
There is a 46.7% increase in the number of bracelets made.
What is Percentage?A percentage is a number or ratio that can be expressed as a fraction of 100 (100 as denominator). To calculate percent of a number, divide the number by the whole and multiply by 100.
Hence, it means, a part per hundred. The word per cent means per 100. It is represented by the symbol “%”.
Maysol made;
This month = 75 bracelets
Last month = 40 bracelets
Change = 75 - 40
Change = 35
This means there was an increase
% increase = (35/75) x 100
% increase = 46.7%
Learn more about percentages here:https://brainly.com/question/19247356
#SPJ1
Use the Table below to find the Average Rate of Change from x = -2 to x = 1. Show your work for full credit.
x f(x)
-3 0
-2 3
-1 4
0 3
1 0
Answers
Answer:
We conclude that:
The average rate = -1
Step-by-step explanation:
We need to find the Average Rate of Change from x = -2 to x = 1.
From the table it is clear that:
at x₁ = -2, f(x₁) = 3
at x₂ = 1, f(x₂) = 0
The formula to determine the average rate of change from x = -2 to x = 1.
Average rate = [f(x₂) - f(x₁)] / [ x₂ - x₁]
= [0 - 3] / [1-(-2)]
= -3 / 3
= -1
Therefore, we conclude that:
The average rate = -1
fill in the mission numbers to make the fractions equivalent. 1/2 and /8= 4/12 and /60= 2/3 and /12= 4/4 and /8=
Answers
To make the fractions equivalent, we need to find the missing numerators that would make them equal. Let's fill in the missing numerators:
1/2 and __/8
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 4:
1/2 and 4/8
Now, the fractions are equivalent.
---
4/12 and __/60
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 5:
4/12 and 20/60
Now, the fractions are equivalent.
---
2/3 and __/12
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 4:
2/3 and 8/12
Now, the fractions are equivalent.
---
4/4 and __/8
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 2:
4/4 and 8/8
Now, the fractions are equivalent.
3/8 + 1/8 - 2/7 + 1/4 equals
Answers
Answer:
Step-by-step explanation: 37/56
PLEASE ANSWER ASAP FOR BRAINESLT!!!!!!!!!!!!!!!!!!

Answers
Step-by-step explanation:
\(a = \pi {r}^{2} \\ a = \pi {5}^{2} = 78.5 \: {in}^{2} \)
Answer:
The area of this circle is 78.5
Step-by-step explanation:
The area of a circle can be calculated with the equation πr². r stands for "radius", the distance between the center of the circle to any point of its edge which also equals to half of a circles diameter. Since the diameter of this circle is 10 in., its radius is
\(r = d/2 = 10/2 = 5\\\)
Then, we use this to find the area
Area =\(\pi r^2=\pi (5)^2=25\pi=78.5\) (rounded to the first decimal place)
Tony rents a bike that costs $4 per hour and $10 for the lock. He has $32 to spend. How long can he rent the bike? Write an equation that represents this situation. Be sure to explain how you got your equation and specify what the variables represent.
Answers
Answer:
5 hours; 4x+10=32
Step-by-step explanation:
4x = 4 multiplied by the amount of hours
10 = the cost for the lock
so y = 4x+10
In this case y= 32 so plug it in
4x+10=32
-10 -10
4x=22
/4 /4
x=5.5
So assuming you can only rent whole hours, it would be 5 hours
Hope this helps.
Answer:
he can rent the bike for 5 hours
Step-by-step explanation:
32-10=22
22*4=5
You invested $4000 between two accounts paying 3% and 4% annual interest. If the total interest earned for the year was $130, how much was invested at each rate?
Answers
You invested $3000 at 3% annual interest rate, and the remaining amount of $4000 - $3000 = $1000 was invested at 4% annual interest rate.
Let's assume you invested an amount, x, at 3% annual interest rate. This means the amount invested at 4% annual interest rate would be $4000 - x.
To calculate the interest earned from the investment at 3%, we multiply x by 3% (0.03). Similarly, the interest earned from the investment at 4% is calculated by multiplying ($4000 - x) by 4% (0.04).
According to the given information, the total interest earned from both investments is $130. So we can set up the equation:
0.03x + 0.04($4000 - x) = $130
Simplifying the equation:
0.03x + 0.04($4000 - x) = $130
0.03x + $160 - 0.04x = $130
-0.01x = $130 - $160
-0.01x = -$30
x = -$30 / -0.01
x = $3000
Therefore, you invested $3000 at 3% annual interest rate, and the remaining amount of $4000 - $3000 = $1000 was invested at 4% annual interest rate.
for such more question on interest rate
https://brainly.com/question/29451175
#SPJ8
HELP ME PLEASE
By which rule are these triangles congruent?
A)
MAS
B)
ASA
SAS
D)
SSS

Answers
Answer:
I brlive the answer is B.........
Answer:
The answer is C) ASA
Step-by-step explanation:
This triangle is ASA because it has two congruent angles shown in the diagram. All of the other answers have none or one. Therefore, it is ASA.
solve for w
w+2/5=3 1/3
Answers
The fractions as 50/15 and 6/15, respectively, and subtract them to obtain w = 44/15. This can be further simplified to the mixed number 2 14/15 or the decimal approximation 2.933.
To solve the equation w + 2/5 = 3 1/3, we need to isolate w on one side of the equation by subtracting 2/5 from both sides, finding a common denominator, and simplifying the resulting expression to obtain w.
w + 2/5 = 10/3
To isolate w, we need to move the constant term on the right-hand side of the equation to the left-hand side by subtracting 2/5 from both sides.
Subtracting 2/5 from both sides:
w = 10/3 - 2/5
To add these fractions, we need to find a common denominator, which is 15. So we can rewrite the fractions as:
w = (50/15) - (6/15)
Combining like terms:
w = 44/15
Therefore, w = 2 14/15 or approximately 2.933.
To learn more about fractions please click on below link
https://brainly.com/question/24370499
#SPJ1
less than a number
Х
A, 12-x
B. 12x
C. X + 12
D. X-12
Answers
Answer:
D) X-12
Step-by-step explanation:
imagine that X = 2 or any number less than 12
A) 12 - X = 12 - 2 = 10
B) 12X = 12 ×2 = 24
C) X + 12 = 2 + 12 = 14
D) X - 12 = 2 - 12 = -10
So, the smallest number is (D)
Hope it's help.
Please anyone help me

Answers
Answer:$2094.00
Step-by-step explanation:Put in desmos calculator and put 4.7 percent of 2000 and you get 94 then add 94 to 2000 and you got $2094
Suppose the x-intercept of f (x) is (P,0) and the x-intercept of g(x) is (7,0). What is the value of p+
M
10
8.
7
ܗ0
5
3
2
g(g)
1
ܝ0ܝܕ
.10 9 .8 -7 . . .4 .5 .2 1 0 1_2_3 4 5 6 7 8 9 10
-1
2-
.3
ܗܿ ܫܼܲ ܪ ܇ ܀ 5
Answers
Answer:
Answer:
D. (-2,-5), (0, -7), (1, -4)
Step-by-step explanation:
From Function Theory we must remember that range of a function is the set of images related to elements of the domain. In this case, we must find the image of each of the three elements that forms the domain of , which are: , and .
Then we proceed to find all elements of range:
Which corresponds to option D.
Step-by-step explanation:
geometry need help asap

Answers
The value of angle LAF in the intersecting chords is determined as 104⁰.
What is the value of angle LAF?The value of angle LAF is calculated by applying intersecting chord theorem, which states that the angle at tangent is half of the arc angle of the two intersecting chords.
Also this theory states that arc angles of intersecting secants at the center of the circle is equal to the angle formed at the center of the circle by the two intersecting chords.
m∠LAF = ¹/₂ (arc LF + arc YS)
From the diagram, we have arc LF = 160⁰ and YS = 48⁰
m∠LAF = ¹/₂ (160 + 48)
m∠LAF = 104⁰
Thus, the value of angle LAF is calculated by applying intersecting chord theorem.
Learn more about chord angles here: brainly.com/question/23732231
#SPJ1
1
If 3 dogs equally share pound of dog
food what share will each dog get?
2
Answers
Answer:
.333 pounds hope this helps
2^(2t)-12(2^(t))+32=0
Answers
Answer:
t = 2 and t = 3.
Step-by-step explanation:
To solve the equation 2^(2t) - 12(2^t) + 32 = 0, we can use a substitution to simplify the equation. Let's set u = 2^t:Substituting u = 2^t, the equation becomes:u^2 - 12u + 32 = 0Now we have a quadratic equation in terms of u. We can solve it by factoring or using the quadratic formula. Let's try factoring:(u - 4)(u - 8) = 0Setting each factor equal to zero, we have:u - 4 = 0 or u - 8 = 0Solving for u:u = 4 or u = 8Now, substitute back u = 2^t:For u = 4:
2^t = 4Taking the logarithm base 2 of both sides:
t = log2(4)
t = 2For u = 8:
2^t = 8Taking the logarithm base 2 of both sides:
t = log2(8)
t = 3
Find the missing angle in the triangle
A. 37 degrees
B. 39 degrees
C. 51 degrees
D. 53 degrees

Answers
sin^-1 (40/50) = 53.13 deg
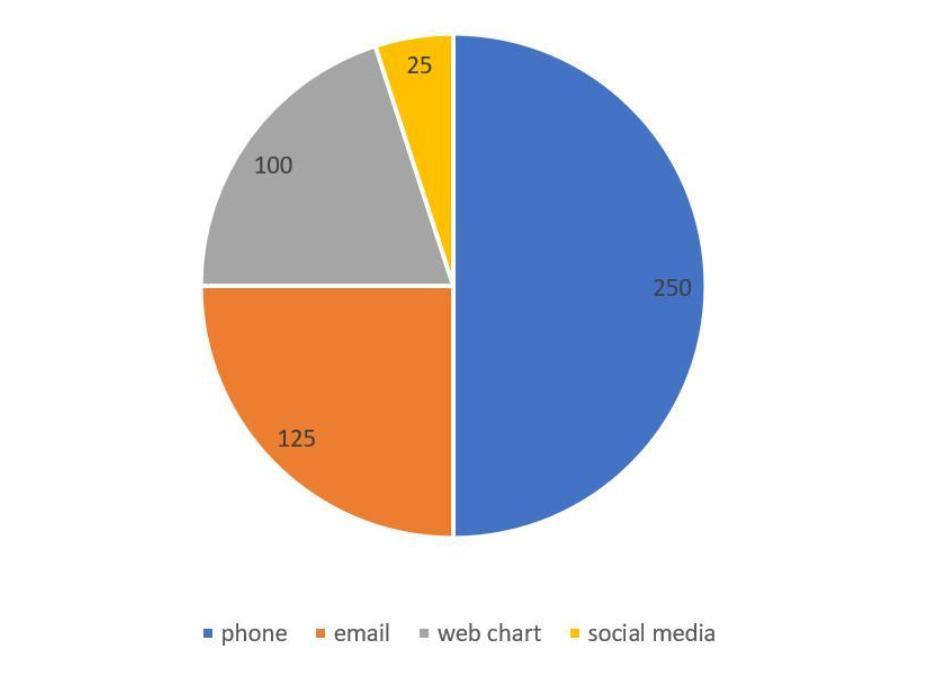
Information
500 customers contacted a company today.
Phone
250 Customers
Webchat
4x Social Media
Email
III)
50% of Phone
Social Media
Question
Adjust the pie chart to represent the source of customer contacts.
G
Answers
Pie graphs can be used to display percentages of an entire group and depict percentages at a certain moment. Customers contacted via the web = x(let) then.as a result, customers contacted online (chart = x = 100), 25 customers were reached by social media, or x/4
What purpose does a pie chart serve?Pie charts can be used to show percentages for the whole group or for a specific time period.
In contrast to bar and line graphs, pie charts do not show changes over time.
The following pages provide descriptions of the various pie chart elements.
Since the slices of a pie chart represent different parts of the whole, their sum must always equal 100%.
Number of customers overall = 250 clients were contacted via email for every 500 customers contacted via phone, or 50% of phone contacts.
=(50÷100)×250
=125
Customers reached via social media
= total customers + 250 + 125 + x+1 = 500 x+1
=125 × 5
T=125
x=100.
Customers contacted via the web = x(let) then.
as a result, customers contacted online (chart = x = 100)
25 customers were reached by social media, or x/4
To learn more about Pie graphs refer
brainly.com/question/26851221
#SPJ1
Please can someone show me their working on these, as I'd really like to know where I went wrong.


Answers
Answer:
C
Step-by-step explanation:
You were on the right track, but 3-2 = 1, so the exponent of (x-4) is 1.
Answer:
C and B
Step-by-step explanation:
(6)
\(\frac{(x-4)^3(3x+6)}{(x-4)^2}\)
Cancel (x - 4)³ on numerator with (x - 4)² on denominator
leaving (x - 4) on numerator and 1 on denominator
= (x - 4)(3x + 6) → C
--------------------------------------------------
Using the rule of exponents
\(a^{m}\) × \(a^{n}\) = \(a^{(m+n)}\) , then
4a² × 7\(a^{\frac{1}{2} }\)
= 4 × 7 × a² × \(a^{\frac{1}{2} }\)
= 28 × \(a^{\frac{4}{2} }\) × \(a^{\frac{1}{2} }\)
= 28 × \(a^{(\frac{4}{2}+\frac{1}{2}) }\)
= 28\(a^{\frac{5}{2} }\) → B
After Game 6 of the 2016 NBA Finals, Frank put down an even-money $100,000 bet on the Cavs to win Game 7 (and therefore, the championship). So, if the Cavs win, he wins $100,000, and if the Cavs lose, he loses $100,000. Suppose Frank has a logarithmic utility-of-wealth function: U(w) = ln(w), and his current wealth is $1,000,000 (one million dollars). Given that he accepted this bet, what can we determine about p, the probability with which Frank believes the Cavs will win Game 7? The goal of this problem is to figure this out. The subparts below will walk you through figuring this out
a) Write down an expression for Frank’s expected utility of wealth, as a function of p, if he takes the bet. [Remember to take into account his current wealth level as well as how winning or losing will change it.]
b) Frank’s other option is to reject the bet. What will his utility of wealth be if he rejects the bet?
c) If he accepts the bet, we know that the utility given for (a) must be larger than the utility given for (b). Write down and solve the inequality. You should be able to determine either a lower bound or upper bound for p, e.g. p ≤ 0.25 or p ≥.80.
d) Suppose Frank’s utility-of-wealth function was less curved, i.e. closer to a straight line. How would the bound from (c) change? Remember, the bound defines the range of possible probabilities p for him to accept the bet. Explain why it would be larger or smaller.
Answers
Frank's expected utility of wealth function if he takes the bet is U(w) = $1,000,000 + p(ln($100,000)) + (1-p)(ln($900,000)). If Frank accepts the bet, the probability p must be greater than or equal to 0.8.
a) Frank's expected utility of wealth if he takes the bet is U(w) = $1,000,000 + p(ln($100,000)) + (1-p)(ln($900,000))
b) If Frank rejects the bet, his utility of wealth will be U(w) = ln($1,000,000)
c) U(w) = $1,000,000 + p(ln($100,000)) + (1-p)(ln($900,000)) ≥ ln($1,000,000)
p(ln($100,000)) + (1-p)(ln($900,000)) ≥ ln($1,000,000) - $1,000,000
p(ln($100,000)) + (1-p)(ln($900,000) - ln($1,000,000)) ≥ -$1,000,000
p(ln($100,000) - ln($1,000,000)) + (1-p)(ln($900,000) - ln($1,000,000)) ≥ -$1,000,000
p(ln($100,000/$1,000,000)) + (1-p)(ln($900,000/$1,000,000)) ≥ -$1,000,000
p(ln(0.1)) + (1-p)(ln(0.9)) ≥ -$1,000,000
p(ln(0.1)) ≥ -$1,000,000 - (1-p)(ln(0.9))
p ≥ (-$1,000,000 - (1-p)(ln(0.9)))/(ln(0.1))
p ≥ -$1,000,000/(ln(0.1)) - (1-p)(ln(0.9))/ln(0.1)
p ≥ 0.8
d) If Frank's utility of wealth function was less curved, i.e. closer to a straight line, the bound from (c) would be larger. This is because, with a less curved utility of wealth function, Frank would be less risk-averse and therefore more likely to accept the bet.
learn more about function here
https://brainly.com/question/12431044
#SPJ4
Write a formula for the area of the regular polygon. Solve the formula for the height h.

Answers
Solution:
Part A:
The image of the regular polygon given is an octagon.
An octagon is a polygon with 8 sides.
To calculate the area of a regular polygon, the polygon is split into triangles and the area of triangles is summed up to get the area of the polygon.
\(\begin{gathered} \text{Area of triangle is given by}; \\ A=\frac{1}{2}bh \\ \text{where b is the base} \\ h\text{ is the height.} \\ \\ A\text{ polygon has n-triangles.} \\ \text{Therefore, the area of a regular polygon is;} \\ A=n\times\frac{1}{2}bh \\ A=\frac{n}{2}bh \\ \\ \text{Also, the perimeter of the polygon is the sum of the outer sides, i.e, the sum of the base.} \\ P=n\times b \\ A=\frac{Ph}{2} \\ \text{For an octagon, n = 8sides} \\ P=8b \\ \\ \text{Thus,} \\ A=\frac{8bh}{2} \end{gathered}\)Therefore, the area of the regular polygon (octagon) is;
\(A=\frac{8bh}{2}\)Part B:
To solve for the formula for the height h, we make h the subject of the formula;
\(\begin{gathered} A=\frac{8bh}{2} \\ \text{Cross multiplying:} \\ 2A=8bh \\ \text{Dividing both sides by 8b;} \\ h=\frac{2A}{8b} \end{gathered}\)Therefore, the height is;
\(h=\frac{2A}{8b}\)Prime number between 60 and 80 with the 10’s digit being one less than the 1st digit
Answers
It would be 89.
You can also just look up a list of prime numbers online.
University of Florida researchers in the Department of Materials Science and Engineering have invented a technique that rapidly detects traces of TNT (Today, Spring 2005). The method, which involves shining a laser on a potentially contaminated object, provides instantaneous results and gives no false positives. In this application, a false positive would occur if the laser detected traces of TNT when, in fact, no TNT were actually present on the object. Let A be the event that the laser light detects traces of TNT. Let B be the event that the object contains no traces of TNT. The probability of a false positive is 0.
Required:
Write this probability in terms of A and B using symbols such as U, ∩ and |.
Answers
Answer:
P(A n B) = 0
Step-by-step explanation:
Given
\(A \to\) Traces of TNT detected
\(B \to\) No traces of TNT
Required
Probability of false positive
From the question, we understand that A and B must occur to get a positive and the result is 0.
The probability of A and B is represented as: P(A n B)
Include the result (0), we get:
P(A n B) = 0
(√14 + √10i)(√14 - √10i)
Answers
Answer:
24
Step-by-step explanation:
You want the value of the product ...
(√14 + √10i)(√14 - √10i)
Difference of squaresThe factoring of the difference of squares is ...
a² -b² = (a +b)(a -b)
Here, we have a=√14 and b=√10i. The product of the sum and difference of these values is ...
(√14 + √10i)(√14 - √10i) = (√14)² -(√10i)²
= 14 -(10(-1)) = 24
The product is 24.
The sum of 3 consecutive integers is 201. What are the integers?
Answers
Answer:
Step-by-step explanation:
the consecutive numbers can be represented by (n-1), n, and (n+1), where n is an integer.
(n-1) + n + (n+1) = 201
3n = 201
n = 67
66, 67, 68
I GIVE YOU BRAINLIST PLZZZZZZZZZ HELP



Answers
brainly is a good app ngl 100 best but I can help hu
Jalen has $25 to make copies of her flyer. If each copy costs 8 cents, how many copies can he make?
Answers
Anita plans to give her husband 3 shirts for his birthday. She narrows the search to 3 shirts from a selection of 17 shirts at Dillon's Store or 3 from a selection of 20 shirts at The Men's Shop. In how many ways can she select the shirts
Answers
Using the combination formula, it is found that she can select the shirts in 775,200 ways.
The order in which the shirt are chosen is not important, hence, the combination formula is used to solve this question.
Combination formula:
\(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by:
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
In this problem:
3 shirts from a set of 17.Then, 3 shirts from a set of 20.They are independent, hence, to find the total, we multiply both combinations.\(T = C_{17,3} \times C_{20,3} = \frac{17!}{3!14!} \times \frac{20!}{3!17!} = 680 \times 1140 = 775200\)
She can select the shirts in 775,200 ways.
To learn more about the combination formula, you can check https://brainly.com/question/25821700