11. Evaluate the integral using the Fundamental Theorem of Calculus. √√1 +63x dx
Answers
To evaluate the integral ∫√√(1 + 63x) dx using the Fundamental Theorem of Calculus, we can follow these steps:
First, let's rewrite the integral in a more manageable form. We have ∫(1 + 63x)^(1/4) dx.
To apply the Fundamental Theorem of Calculus, we need to find the antiderivative of (1 + 63x)^(1/4). We can do this by using the power rule for integration, which states that the integral of x^n dx, where n is not equal to -1, is (1/(n + 1))x^(n+1) + C.
Applying the power rule, we integrate (1 + 63x)^(1/4) as (4/5)(1 + 63x)^(5/4) + C.
Therefore, the integral ∫√√(1 + 63x) dx evaluates to (4/5)(1 + 63x)^(5/4) + C, where C is the constant of integration.
By applying the Fundamental Theorem of Calculus and finding the antiderivative of the integrand, we can evaluate the given integral and obtain the final result as (4/5)(1 + 63x)^(5/4) + C.
Learn more about integral here: brainly.com/question/31433890
#SPJ11
Related Questions
helpppppppppppppppppppppppppppp

Answers
Answer:
96
Step-by-step explanation:
First we have to see how the pattern is increasing.
How did the sequence of numbers get from -3 to 6?
Try adding first.
To get from -3 to 6, add 9.
Move on to the next nunber.
Can we get from 6 to -12 through the same pattern (adding 9)?
No, so addition is not the pattern.
Next try multiplication.
To get from -3 to 6, multiply -2.
Move on to the next number.
Can we get from 6 to -12 through the same pattern (multiplying by -2)?
Yes!
Check the other numbers.
-12 × -2 = 24
24 × -2 = -48
Do they meet the pattern?
Yes!
To find the next number in the sequence, use the pattern: multiply the previous number by -2.
-48 × -2 = 96
Answer:
36 i think , datsss confusin Asfkkkkkkk
Step-by-step explanation:
a date is called weird if the number of its month and the number of its day have greatest common factor 1. what are the fewest number of weird days in any month?
Answers
Numbers which are co- prime number which have greatest common factor one are 1, 7, 13, 17, 19, 23, 29, 31
Define co prime numbers.Two integers a and b are coprime, comparatively prime, or mutually prime in mathematics if and only if the single positive integer that divides both of them is 1. As a result, every prime integer that divides a does not divide b, and the opposite is also true. This translates to having a greatest common divisor of 1 for them. Co-prime numbers are collections of numbers with just one common factor between them. Their highest common factor (HCF) is 1, which signifies. For Co-Primes to exist, there must be at least two Numbers. Relatively Prime Numbers is another name for co-prime numbers.
Given,
A date is called weird if the number of its month and the number of its day have greatest common factor 1.
Numbers which are co- prime which have greatest common factor one are:
1, 7, 13, 17, 19, 23, 29, 31
To learn more about co prime number, visit:
https://brainly.com/question/28643898
#SPJ4
An Urn Contains Two Black Balls And Three White Balls. Two Balls Are Selected At Random From The Urn Without Replacement And
Answers
In this problem, we have an urn containing two black balls and three white balls.
We are randomly selecting two balls from the urn without replacement, meaning that once a ball is selected, it is not put back into the urn before selecting the second ball. We need to find the probability that both balls selected are white.
To solve this problem, we can use the concept of conditional probability. The probability of both balls being white can be calculated as the product of two probabilities: the probability of selecting the first white ball and the probability of selecting the second white ball given that the first ball was white.
The probability of selecting the first white ball is 3/5, as there are three white balls out of a total of five balls in the urn. After removing one white ball from the urn, there are four balls remaining, with two of them being white. Therefore, the probability of selecting the second white ball given that the first ball was white is 2/4 or 1/2.
By multiplying the probabilities, we get (3/5) * (1/2) = 3/10. Therefore, the probability that both balls selected are white is 3/10 or 0.3.
The probability of selecting two white balls from an urn containing two black balls and three white balls, without replacement, is 3/10 or 0.3. This probability is calculated using the concept of conditional probability, multiplying the probability of selecting the first white ball by the probability of selecting the second white ball given that the first ball was white.
Learn more about probability here: brainly.com/question/31828911
#SPJ11
Fritz can build a bookcase in 8 hours and Holly can build the same bookcase in 10 hours. After working together for 3 hours, Fritz leaves how long will it take holly to finish the bookcase by herself?
Answers
Holy will take 13/5 or 2.6 hours to finish the bookcase.
What is relation between time and work?The relation between time and work is
Work Done = Time Taken × Rate of Work ·
or, Rate of Work = 1 / Time Taken ·
or, Time Taken = 1 / Rate of Work ·
Now it is given that,
Time taken by Fritz to build a bookcase = 8 hours
So, Bookcase build by Fritz in 1 hour = 1/8
Similarly,
Time taken by Holly to build a bookcase = 10 hours
So, Bookcase build by Holly in 1 hour = 1/10
So, bookcase build in 3 hours
Fritz = 3/8
Holly = 3/10
Total bookcase build in 3 hours = 3/8 + 3/10 = 27/40
So. remaining work = 1 - 27/40 = 13/40
Thus, Time taken by Fritz to complete the bookcase = 8 * (13/40) hours
= 13/5 or 2.6 hours
Thus, Holy will take 13/5 or 2.6 hours to finish the bookcase.
To learn more about work and time:
brainly.com/question/24253661
#SPJ4
Pls help due ASAP .....

Answers
Answer:
15
Step-by-step explanation:
The angles are opposites, so they're congruent.
4x - 5 = 3x + 10
4x - 3x = 10 + 5
x = 15
Give an example of joint random variable X and Y such that (i) H(Y∣X=X)H(Y)
Answers
H(Y∣X=X)H(Y) holds for the given joint random variable X and Y.
Given that we have to provide an example of a joint random variable X and Y such that
(i) the entropy of Y given X = x is smaller than the overall entropy of Y.
H(Y∣X=X)H(Y)We have to choose X and Y in such a way that it fulfills the above condition. The entropy of Y given that X = x (H(Y|X = x)) can be defined as follows:
H(Y|X=x) = − ∑i p(Y=yi|X=x) log p(Y=yi|X=x) .Therefore, we must choose X and Y such that H(Y) < H(Y|X=x), or in other words, the entropy of Y given X = x is smaller than the overall entropy of Y.
Example:
Let us take X and Y as 2 random variables such that X takes values -1,0,1 and Y takes values 0,1 such that P(X = -1) = 1/3, P(X = 0) = 1/3, P(X = 1) = 1/3, P(Y = 0) = 1/2, P(Y = 1) = 1/2.
The joint distribution can be represented in the following table:
Therefore, H(Y) = −(1/2 log(1/2) + 1/2 log(1/2)) = 1 bit And,H(Y|X=-1) = −(1/2 log(1/2) + 0 log(0)) = 1/2 bit Similarly,H(Y|X=0) = −(1/2 log(1/2) + 1/2 log(1/2)) = 1 bit And,H(Y|X=1) = −(0 log(0) + 1/2 log(1/2)) = 1/2 bit
Hence, H(Y∣X=X)H(Y) holds for the given joint random variable X and Y.
learn more about variable in the link:
https://brainly.com/question/28248724
#SPJ11
Hector is visiting a cousin who lives 310 miles away he has driven a hundred miles how many more miles does he need to drive to riches cousins home let Z be how many miles left to riches cousins home
Answers
Ambrose has an indifference curve with equation x2=20-4x^1/2*1. When Ambrose is consuming the bundle (4,16), his marginal rate of substitution is 25/4
Answers
The indifference curve equation given is x2 = 20 - 4x^(1/2)*1, where x1 and x2 represent the quantities of two goods Ambrose is consuming.
The marginal rate of substitution (MRS) measures the rate at which Ambrose is willing to trade one good for the other while remaining on the same indifference curve. It is calculated as the negative ratio of the derivatives of the indifference curve with respect to x1 and x2, i.e., MRS = -dx1/dx2. Given that Ambrose is consuming the bundle (4,16), we can substitute these values into the indifference curve equation to find the corresponding MRS. Plugging in x1 = 4 and x2 = 16, we have: 16 = 20 - 4(4)^(1/2)*1; 16 = 20 - 8; 8 = 8. This confirms that the bundle (4,16) lies on the indifference curve. Now, we are given that the MRS at this point is 25/4.
Therefore, we can set up the following equation: dx1/dx2 = 25/4. Simplifying, we have: dx1/dx2 = -25/4. This indicates that the rate at which Ambrose is willing to trade good x1 for good x2 at the bundle (4,16) is -25/4. The MRS represents the slope of the indifference curve at a given point and reflects the trade-off between the two goods. In this case, it indicates that Ambrose is willing to give up 25/4 units of good x1 in exchange for one additional unit of good x2 while maintaining the same level of satisfaction.
To learn more about curve equation click here: brainly.com/question/28569209
#SPJ11
Find the sum or difference.
(- 2h + 1) + 2(3h - 4) SHOW YOU WORK FOR POINTS AND BRAINIEST
Answers
Answer: (- 2h + 1) + 2(3h - 4) = 4h -7
Step-by-step explanation:
First, remove unnecessary parentheses
- 2h + 1 + 2(3h - 4)
then distribute 2 through the parentheses
- 2h + 1 + 2(3h - 4) = -2h + 1 + 6h -8
Combine like terms
-2h + 1 + 6h -8 = 4h + 1 - 8
1-8= 7
So the answer is
4h - 7
which of the following statements are true for a frequentist definition for the probability of an event g
Answers
The frequentist probability is objective, based on observed data, need large sample or long term frequency, and doesn't have prior knowledge.
What is frequentist probability?Frequentist probability is a definition of probability that defines the probability of an event as the probability of an event being observed in a long-term or infinite experiment.
Frequentist probability is different from Bayesian probability in following points,
Frequentist is objective and Bayesian is subjectiveFrequentist based on observed data and Bayesian based on degree of beliefFrequentist need large sample and Bayesian not necessary need large sampleFrequentist reject the prior assumption or knowledge and Bayesian need prior assumption or knowledge for parameterThus, the statement are true for frequentist definition for the probability is doesn't have prior knowledge, need large sample, based on observed data, and objective.
Your question is incomplete, but it is general information about the frequentist definition of probability.
Learn more about frequentist here:
brainly.com/question/29103614
#SPJ4
Which sign will you put in between [ 120 ……… (3 / 11) ], so that the answer is the highest number
a) +
b) –
c) x
d) ÷
Answers
Answer:
d) ÷
Step-by-step explanation:
120 ÷ 3/11 = 440
FILL THE BLANK. The average time a molecule spends in its reservoir is known as ________.
Answers
The average time a molecule spends in its reservoir is known as the residence time.
Residence time is an important concept in environmental science, particularly in the study of water quality and pollution. It refers to the average amount of time that a substance, such as a molecule or a pollutant, spends in a particular environment before it is either removed or transformed. For example, in a river, the residence time of a pollutant would be the amount of time it takes for that pollutant to be either broken down by natural processes or transported downstream to another location. By understanding residence time, scientists can better predict how pollutants will move through the environment and where they are likely to accumulate.
Learn more about average time here
https://brainly.com/question/15418098
#SPJ11
the midpoint of ab is m (3,-4). If the coordinates of A are (8,-5), what are the coordinates of B
Answers
Answer:
work is attached and shown

The coordinates of the midpoint will be (-2,-3).
What is coordinate geometry?A coordinate plane is a 2D plane that is formed by the intersection of two perpendicular lines known as the x-axis and y-axis. A coordinate system in geometry is a method for determining the positions of the points by using one or more numbers or coordinates.
A midpoint is a point that lies on a line connecting two other locations and is in the middle of the line. Given that the midpoint of AB is M(3,-4) and the coordinates of A are (8, -5).
The midpoint will be calculated by using the formula below:-
( 8 + x ) / 2 = 3
( 8 + x ) = 6
x = -8 + 6 = -2
( -5 + y ) / 2 = -4
( -5 + y ) = -8
y = -8 + 5 = -3
Therefore, the coordinates of the midpoint will be (-2,-3).
To know more about Coordinate geometry follow
brainly.com/question/18269861
#SPJ2
Paul thinks of three numbers, which he calls a, b and c.
The ratio a: c is 10: 3.
The ratio b: cis 7 : 2.
The median of a, b and c is 80.
Work out the values of a, b and c.
Answers
Since the median of a, b and c is 80, the values of a, b and c are 22.86, 80, and 76.2 respectively.
What is a median?In Mathematics, a median can be defined as the middle number (center) of a sorted data set, which is when the data set is arranged in from the greatest to least or the least to greatest.
From the data set, we have the following ratios:
a: c = 10/3 = 10: 3.
b: c = 7/2 = 7 : 2
Next, we would determine the smallest number when the data set is ordered in ascending order:
10/3 = 7/2
2 × (10/3) = (7/2) × 3
20/6 = 21/6
Therefore, c < a < b as 20 is less than 21 and the variable a represent the median.
For the value of c, we have:
80 = (7/2) × c
c = (2/7) × 80
c = 160/7
c = 22.86.
For the value of b, we have:
b = (10/3) × c
b = (10/3) × 22.86
b = 228.6/3
b = 76.2.
Read more on median here: brainly.com/question/452652
#SPJ1
hey! i’ll give brainliest please help

Answers
Answer:
conjunction
Step-by-step explanation:
Answer:
Conjunction is correct answer. (I think)
Type in the value of y.
If x = 7, then y =
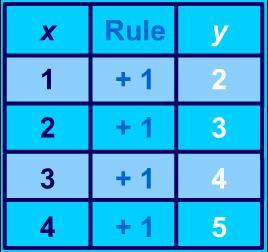
Answers
Explanation:
The rule says "whatever x is, add 1 to it to get y"
So for instance, if x = 3, then y = x+1 = 3+1 = 4
Now if x = 7, then y = x+1 = 7+1 = 8
Answer:
\(\huge\boxed{Answer\hookleftarrow}\)
Given that,
\(1 + 1 = 2 \\ 2 + 1 = 3 \\ 3 + 1 = 4 \\ 4 + 1 = 5...\)
So from this we can infer that, \(\large\bold{ x + 1 = y}\)
Now,
\(x = 7 \\ y= \: ?\)
Use the rule ⎆ \(\large\bold{ x + 1 = y}\)
\(x + 1 = y \\ 7 + 1 = y \\ 8 = y\)
✐ The value of y is 8.
ʰᵒᵖᵉ ⁱᵗ ʰᵉˡᵖˢ
# ꧁❣ RainbowSalt2²2² ࿐
What is the difference

Answers
Answer:
+4
Step-by-step explanation:
-5 - (-9)
-5 + 9
4
Answer:
4
Hope this helped and if I'm wrong sorry
Find the real part of the particular solution Find the real part of the particular solution to the differential equation dแบกy 3 dt2 dy +5 + 7y =e3it dt in the form y=Bcos(3t) + C sin(3t) where B, C are real fractions. Re(y(t)) =____
Answers
The real part of the particular solution to the differential equation is Re(y(t)) = (5 / 106) cos(3t).
We can start by assuming that the particular solution to the differential equation is of the form y = A e^(3it), where A is a complex constant that we need to determine.
We first take the first and second derivatives of y with respect to time:
dy/dt = 3i A e^(3it)
d^2y/dt^2 = -9 A e^(3it)
Substituting these into the differential equation, we get
-27i^2 A e^(3it) + 15i A e^(3it) + 7A e^(3it) = e^(3it)
Simplifying, we get
(-27 + 15i)A e^(3it) + 7A e^(3it) = e^(3it)
Factorizing, we get
(-27 + 15i + 7)A e^(3it) = e^(3it)
Solving for A, we get
A = 1 / (5 - 9i)
To find the real part of y, we can use Euler's formula
e^(3it) = cos(3t) + i sin(3t)
Substituting for A, we get
y = A e^(3it)
y = (1 / (5 - 9i)) (cos(3t) + i sin(3t)) e^(3it)
y = (1 / (5 - 9i)) [(cos(3t) + i sin(3t)) (cos(3t) + i sin(3t))] e^(3it)
y = (1 / (5 - 9i)) [(cos^2(3t) - sin^2(3t)) + 2i sin(3t) cos(3t)] e^(3it)
Taking the real part, we get
Re(y) = (1 / (5 - 9i)) (cos^2(3t) - sin^2(3t))
Re(y) = (1 / (5 - 9i)) (cos(6t))
Re(y) = (5 / 106) cos(3t)
Learn more about differential equation here
brainly.com/question/13426876
#SPJ4
The given question is incomplete, the complete question is:
Find the real part of the particular solution Find the real part of the particular solution to the differential equation dạy 3 d^2y/dt^2 +5dy/dt + 7y =e^(3it) in the form y=Bcos(3t) + C sin(3t) where B, C are real fractions. = Re(y(t)) = ?
Homework: Section 11.1 Question 7. Complete the square to find the x-intercepts of the function given by the equation listed. f(x)=x² +34x+104 What are the x-intercepts? **** (Simplify your answer. T
Answers
Answer:
x² + 34x + 104 = 0
x² + 34x = -104
x² + 34x + ((1/2)(34))² = -104 + ((1/2)(34))²
x² + 34x + 17² = -104 + 17²
x² + 34x + 289 = 185
(x + 17)² = 185
x + 17 = +√185
x = -17 + √185
at a party there are only single women and married men with their wives. the probability that a randomly selected woman is single is $\frac{2}{5}$. what fraction of the people in the room are married men?
Answers
60% of the people in the room are married men.
We can use the information that the probability of a randomly selected woman being single is 2/5 to find the fraction of people in the room who are married men.
Let's call the fraction of people in the room who are married men x. The fraction of people in the room who are single women is (2/5) and the fraction of people in the room who are married men and their wives is (1-x)
Since there are only single women and married men with their wives at the party, we know that the sum of the fractions of single women and married men and their wives must be 1.
(2/5) + (1-x) = 1
We can solve this equation for x:
x = 1 - (2/5) = 3/5
So the fraction of people in the room who are married men is 3/5 or 0.6
So, 60% of the people in the room are married men.
Learn more about probability:
https://brainly.com/question/30034780
#SPJ4
NEED ANSWER! The cost of renting a car is $26.50 plus $10 pe rday. sales tax is 6% select the two expression that represent the cost of renting a car for d days.
A.28.09d
B.26.50+6d
C.26.50+1.06d
D. 28.09+10.6d
E.1.06(26.50+10d)

Answers
Answer:
E.1.06(26.50+10d)
Step-by-step explanation:
d+e
i think i its d im not sure to
Find each unit rate. Round to the nearest hundredth if necessary

Answers
Answer:
the answer: 30 people per class
Using the equation (3), prove q(t) = q0 * exp(-t/RC)
Note Equation (3) is q/C + I*Rv=0
Answers
We have proved that q(t) = q0 * exp(-t/RC) using the given equation (3).
To prove q(t) = q0 * exp(-t/RC) using the equation (3), let's follow these steps:
1. Rewrite equation (3) as I = -q/C - Rv. Since I = dq/dt (the rate of change of charge q with respect to time t), we get dq/dt = -q/C - Rv.
2. Notice that Rv term in the equation involves the product of resistance (R) and voltage (V). However, voltage across the capacitor is V = q/C. Thus, Rv = R(q/C).
3. Substitute this back into the equation: dq/dt = -q/C - R(q/C).
4. Simplify the equation: dq/dt = -(1/RC)q.
5. This is a first-order linear ordinary differential equation. To solve it, separate variables and integrate both sides:
∫(1/q) dq = ∫-(1/RC) dt.
6. Integrating both sides gives: ln(q) = -t/RC + C1, where C1 is the integration constant.
7. Taking the exponent of both sides to eliminate the natural logarithm: q(t) = exp(-t/RC + C1).
8. We can rewrite the exponent as: q(t) = exp(-t/RC) * exp(C1).
9. Since exp(C1) is just another constant, we can denote it as q0 (initial charge at t=0): q(t) = q0 * exp(-t/RC).
Thus, we have proved that q(t) = q0 * exp(-t/RC) using the given equation (3).
To learn more about integration, refer below:
https://brainly.com/question/30900582
#SPJ11
The perimeter of a rectangle is 52 feet. The length is 2 more than twice the width. What is the length of the rectangle?
Answers
Answer: The Length of the rectangle is 18 feet.
The width is 8 feet
Step-by-step explanation: Perimeter is 2w + 2L
Length here is 2w + 2 Substitute this value for L in the equation.
P = 2w + 2L
52 = 2w + 2(2w + 2) distribute and add
52 = 2w + 4w + 4
52 = 6w + 4 Subtract 4 from both sides, Then divide both sides by 6 to solve for w
48 = 6w
8 = w The width is 8 ft
Substitute into the original expression for Length
Length here is 2w + 2 : 2(8) + 2 16 + 2 = 18
The Length is 18 feet.
Check: in the original equation P = 2w + 2L
52 = 2(8) + 2(18)
52 = 16 + 36 TRUE!
Answer:
The length would be 18ft the width would be 8ft
Step-by-step explanation:
In an attempt to avoid a ________ from becoming generic, companies may use it as an adjective describing the category the product belongs to, like Jell-O Brand Gelatin.
Answers
To prevent a trademark from becoming generic, companies often utilize it as an adjective to describe the product category it belongs to, as seen with examples like Jell-O Brand Gelatin.
Trademarks are valuable assets for companies as they distinguish their products or services from those of competitors. However, if a trademark becomes generic, it loses its distinctiveness and legal protection. When a trademark becomes a common name for a particular product or service, it is no longer associated exclusively with a specific brand.
To prevent this from happening, companies may use their trademarked name as an adjective to describe the category or type of product it represents. For instance, Jell-O is a well-known brand for gelatin, and the company uses the term "Jell-O Brand Gelatin" to emphasize that Jell-O is a specific brand within the gelatin category.
By using the trademark as an adjective, companies aim to reinforce the connection between their brand and the product category while maintaining the distinctiveness and exclusivity of their trademark. This practice helps protect the trademark's strength and prevents it from becoming a generic term that any company can use, thus preserving its legal protection and brand identity.
Learn more about gelatin category here:
https://brainly.com/question/28045157?
#SPJ11
1. Dilate A using
Pas the center
of dilation and a
scale factor of 3.
Label the new
point P.
B.
Pear Deck Interactive Side
Do not remove the
Students, draw anywhere on this slide!

Answers
Camilla borrows a book from the library for dd days. The library charges a late fee of 0. 10 dollars per day that the book is late. If Camilla returns the book more than 21 days after she borrowed it, the expression 0. 10(d-21) represents the total late fee Camilla owes
Answers
The expression represents the amount of total money. Then the total late fee Camilla owes will be $2.1.
What is Algebra?
Algebra is the study of graphic formulas, while logic is the interpretation among those signs.
Camilla borrows a book from the library for d days.
The library charges a late fee 0.10 dollars per day that the book is late.
If Camilla returns the book more than 21 days after she borrowed it.
Then the expression will be 0.10d.
The total amount is given as
Total amount = 0.10 d
Total amount = 0.10 x 21
Total amount = $2.1
learn More about of Algebra here
https://brainly.com/question/11841980
#SPJ4
Assume there is a sample of n
1
=4, with the sample mean
X
1
=35 and a sample standard deviation of S
1
=4, and there is an independent sample of n
2
=5 from another population with a sample mean of
X
ˉ
2
=31 and a sample standard deviation S
2
=5. In performing the pooled-variance t test, how many degrees of freedom are there? There are degrees of freedom. (Simplify your answer.)
Answers
There are 7 degrees of freedom.
In performing the pooled-variance t test, the degrees of freedom can be calculated using the formula:
df = (n1 - 1) + (n2 - 1)
Substituting the given values:
df = (4 - 1) + (5 - 1)
df = 3 + 4
df = 7
Therefore, there are 7 degrees of freedom.
Learn more about degrees of freedom
brainly.com/question/32093315
#SPJ11
There are 7 degrees of freedom for the pooled-variance t-test.
To perform a pooled-variance t-test, we need to calculate the degrees of freedom. The formula for degrees of freedom in a pooled-variance t-test is:
\(\[\text{{df}} = n_1 + n_2 - 2\]\)
where \(\(n_1\)\) and \(\(n_2\)\) are the sample sizes of the two independent samples.
In this case, \(\(n_1 = 4\)\) and \(\(n_2 = 5\)\). Substituting these values into the formula, we get:
\(\[\text{{df}} = 4 + 5 - 2 = 7\]\)
In a pooled-variance t-test, we combine the sample variances from two independent samples to estimate the population variance. The degrees of freedom for this test are calculated using the formula \(df = n1 + n2 - 2\), where \(n_1\)and \(n_2\) are the sample sizes of the two independent samples.
To understand why the formula is \(df = n1 + n2 - 2\), we need to consider the concept of degrees of freedom. Degrees of freedom represent the number of independent pieces of information available to estimate a parameter. In the case of a pooled-variance t-test, we subtract 2 from the total sample sizes because we use two sample means to estimate the population means, thereby reducing the degrees of freedom by 2.
In this specific case, the sample sizes are \(n1 = 4\) and \(n2 = 5\). Plugging these values into the formula gives us \(df = 4 + 5 - 2 = 7\). Hence, there are 7 degrees of freedom for the pooled-variance t-test.
Therefore, there are 7 degrees of freedom for the pooled-variance t-test.
Learn more about t-test
https://brainly.com/question/13800886
#SPJ11
pls
ef F F. dr using the Fundamental Theorem of Line Integrals. Use a computer algebra system to verify your results. S (3z + 2y) dx + (2x - 2z) dy+ (3x - 2y) dz (a) C: line segment from (0, 0, 0) to (1,
Answers
1) The line integral value is : ∫F dr = 6
2) The line integral value is : ∫F dr = 6
3) The line integral value is : ∫F dr = 6
Here we are given:
\(F.dr = (3x + 2y)dx + (2x -2z)dy + (3x -2y)dz,\)
where\(\vec{F}\) is a conservative field
So,
f(x, y , z) = \(\int\limits (3x + 2y)dx + (2x -2z)dy + (3x -2y)dz,\)
f(x , y , z) = (3zx +2yx) + (2xy - 2zy) + (3xz - 2yz) + c(x , y , z)
\(f(x, y, z) = (6xz + 4xy - 4yz) + c(x, y, z)\)
Now substitute the values of x , y ,z ,
1)
Line segment from (0, 0 , 0) to (1,1 ,1)
∫F dr = f(1,1,1) - f(0,0,0)
= |6 + 4 - 4 |- |0 + 0 - 0|
∫F dr = 6
2)
Line segment from (0,0,0) to (0,0,1) to (1,1,1)
First we take (0,0,0) to (0,0,1)
\(\int _c \vec{F}.\vec{dr}=f(0,0,1)-f(0,0,0) =[6(0)(1)+4(0)(0)-4(0)(1)]-[6(0)(0)+4(0)(0)-4(0)(0)] =[0+0-0]-[0+0-0]\)
∫F dr = 0
\(\Rightarrow \int _{c}\vec{F}.\vec{dr}=0+6 [F.dr = 6\)
3)
Line segment from (0,0,0) to (1,0,0) to (1,1,0) to (1,1,1)
First we take (0,0,0) to (1,0,0)
\(\int _c \vec{F}.\vec{dr}=f(1,0,0)-f(0,0,0) =[6(1)(0)+4(1)(0)-4(0)(0)]-[6(0)(0)+4(0)(0)-4(0)(0)] =[0+0-0]-[0+0-0]\int _{c}\vec{F}.\vec{dr}=0\)
Next we take (1,0,0) to (1,1,0)
\(\int _c \vec{F}.\vec{dr}=f(1,1,0)-f(1,0,0) = [6(1)(0) + 4(1)(1) − 4(1)(0)] - [6(1)(0) + 4(1)(0) — 4(0)(0)] = [0+4-0] - [0+0-0]\int _{c}\vec{F}.\vec{dr}=4\)
Lastly we take (1,1,0) to (1,1,1)
\(F.dr = f(1,1,1) ƒ(1,1,0) = [6(1)(1) +4(1)(1) − 4(1)(1)] - [6(1)(0) + 4(1)(1) — 4(1)(0)] =[6+4-4]-[0+4-0]\int _{c}\vec{F}.\vec{dr}=2\)
Adding the three results we get
\(\Rightarrow \int _{c}\vec{F}.\vec{dr}=0+4+2\\\\\int\limits F.dr = 6\)
Therefore we see that the Line integral for the three cases comes out to be same between the initial and final points since it is independent of the path taken.
Know more about line integral ,
https://brainly.com/question/29850528
#SPJ4
8x-10 + 3x+3 solve for x
Answers
Answer:
\(11x + 13\)
Step-by-step explanation:
\(1. \: (8x + 3x) + (10 + 3) \\ 2. \: 11x + 13\)