[12] A + 2.4 = 6.75, A =
Answers
Ans:-
\( \large \tt{ \green{A = 4.35}}\)Solution:-
\(\large \tt{A + 2.4 = 6.75}\)
\( \: \)
\( \tt \large{A = 6.75-2.4}\)\( \: \)
\( \large\underline{ \boxed{ \tt{ \blue{A = 4.35}}}}\)\( \: \)
hope it helps!:)
Related Questions
Use the commutative property to create equivalent expressions. Which expressions are equivalent to 2.2t + 3.5 + 9.8? Check all that apply.
3.5 + 2.2t + 9.8
3 + 2t + 9
2.2 + 3.5 + 9.8t
9.8 + 3.5 + 2.2t
2.2t + 9.8 + 3.5
2.2t + 35.98
hurry plz
Answers
Answer:
A D and E
Step-by-step explanation:
I did it on e2020 and it was right
Answer:
The correct answers are:
A: 3.5 + 2.2t + 9.8
D: 9.8 + 3.5 + 2.2t
E: 2.2t + 9.8 + 3.5
Step-by-step explanation:
Hope this helps!
THIS IS AN EMERGENCY PLEASE HELP ME!!!!!!!!!
With a coupon, you can get a pair of shoes that normally costs $80 for only $68. What percentage was the discount?
Answers
Answer:
Not sue but I think it’s 12%
Step-by-step explanation:
Find the equation of the line that passes through (1,3) and is perpendicular to 2 y = 2 x − 1 . Leave your answer in the form y = m x + c
Answers

in the computer lab there are 14 apple computers and 16 PC computers
approximately what percent of the computer are PCs
Answers
Answer:
14 + 16 = 20
16/20
= 80/100
80 %
Step-by-step explanation:
Answer:
Find the percentage of PCs
Total is 14+16=30 computers
PCs are 16
so, 16/20×100%= 80%
enter an expression equivalent to (x^4y^3y)^2 in the form x^my^n
Answers
The equivalent expression to the expression given; (x⁴y³y)² such that it takes the form; x^my^n is; x⁸• y⁸.
What is the equivalent expression to the expression given (x⁴y³y)² in the form; x^m y^n?It follows from the task content that the given expression is; (x⁴y³y)².
Also, it is required that the expression be written such that we have an expression of the form; x^m y^n.
On this note, the equivalent expression can be determined by the laws of indices as follows;
= (x⁴y⁴)².
By distributing the exponent, then we have;
= x⁸• y⁸
Ultimately, the equivalent expression to the expression given; (x⁴y³y)² such that it takes the form; x^my^n is; x⁸• y⁸.
Read more on equivalent expressions;
https://brainly.com/question/14507158
#SPJ1
Construct a truth table for each of these compound propositions
a) p → ⇁p
b) p ↔ ⇁p
c) p ⊕ (p V q) d) (p ∧ q) → (p V q) e) (p → ⇁p) ↔ (p ↔ q) f) (p ↔ q) ⊕ (p ↔ ⇁q)
Answers
After considering the given data we conclude that there truth table is possible and is placed in the given figures concerning every sub question.
A truth table is a overview that projects the truth-value of one or more compound propositions for each possible combination of truth-values of the propositions starting up the compound ones.
Every row of the table represents a possible combination of truth-values for the component propositions of the compound, and the count of rows is described by the range of possible combinations.
For instance, if the compound has just two component propositions, it comprises four possibilities and then four rows to the table. The truth-value of the compound is projected on each row comprising the truth functional operator.
To learn more about truth table
https://brainly.com/question/28605215
#SPJ4



due now pls help!!!!!!!!!!!

Answers
Answer:
A and D
Step-by-step explanation:
so sorry im in school
x+y=4
-y. -y
x=4-y
4-y-y=2
4-2y=2
-4 -4
-2y= -2
/-2. /-2
y=1
x+1=4
-1 -1
x=3
so A and D is correct
The equation for line s can be written as x - y = -2. Line t is perpendicular to lines and passes through (-4, 1). What is the equation of line t?
Answers
=========================================================
Explanation:
Anything perpendicular to Ax+By = C is of the form Bx-Ay = D
The given equation is x-y = -2 showing that A = 1, B = -1 and C = -2.
So Bx-Ay = D will update to -x-y = D
Plug in the coordinates of (-4,1) to find D.
-x-y = D
D = -x-y
D = -(-4)-1
D = 4-1
D = 3
We go from -x-y = D to -x - y = 3
Then multiply both sides by -1 to end up with x + y = -3
the side lengths of an equiangular octagon are $1$, $2$, $3$, $4$, $1$, $2$, $3$, and $4$ in clockwise order. find the octagon's area.
Answers
The side lengths of an equiangular octagon are 1, 2, 3, 4, 1, 2, 3, and 4 in clockwise order so area of octagon is 11 + 12√2 square units.
The sides of octagon are 1, 2, 3, 4, 1, 2, 3, 4 as shown in the figure,
The area of the octagon = area of the rectangle - the area of the four right isosceles triangular corners.
A = (lxb) - 1/2[√2×√2 + √8×√8]x2
A = [(3+√2+√8)(1+√2+√8)] -1/2[√2×√2 + √8×√8 + √2×√2 + √8×√8]
A = 3 + 12√2 +7
A = 11 + 12√2
Therefore, The area of the octagon is 11 + 12√2 square units.
A closed two-dimensional shape having eight sides, eight vertices, and eight internal angles is known as an octagon. An octagon is referred to as a regular octagon if all of its sides and internal angles are of equal length; otherwise, it is referred to as an irregular octagon. The next sections also discuss the various octagon types, such as convex and concave octagons.
Learn more about Area of octagon:
https://brainly.com/question/860089
#SPJ4

1) Heather spent $360 on pairs of pants. Dress pants cost $80 and jeans cost $40. If she bought a total of 6, then how many of each kind did she buy!
Answers
Answer:
3 dress pants and 3 jeans
Step-by-step explanation:
dress pants cost $80
jeans cost $40
80+40+80+40+80+40= 360
find the npv and irr
if annual discount rate is 8% and
-860 in year 1, $920 in year 3
Answers
The NPV is -$37.65 and the IRR is approximately 11.55%. To calculate the net present value (NPV) and internal rate of return (IRR), we need to consider the cash flows and the discount rate.
Given cash flows:
Year 0: $0
Year 1: -$860
Year 3: $920
Discount rate: 8%
First, let's calculate the present value (PV) of each cash flow using the discount rate:
Year 0: $0 (no cash flow)
Year 1: PV = -$860 / (1 + 0.08)^1 = -$796.30
Year 3: PV = $920 / (1 + 0.08)^3 = $758.65
Now we can calculate the NPV by summing up the present values of all cash flows:
NPV = PV(year 1) + PV(year 3)
= -$796.30 + $758.65
= -$37.65
The NPV is -$37.65.
To calculate the IRR, we need to find the discount rate that makes the NPV equal to zero. In this case, we can use the trial and error method or utilize financial software or calculators to find the IRR. Let's assume the IRR is r%.
Using the cash flows and the IRR:
Year 0: $0
Year 1: -$860
Year 3: $920
Setting the NPV equal to zero:
0 = PV(year 1) + PV(year 3)
\(0 = -$860 / (1 + r)^1 + $920 / (1 + r)^3\)
Solving this equation for r gives us the IRR. However, solving this equation analytically can be complex, so it's better to use financial software or calculators.
Using a financial calculator or software, the IRR for these cash flows can be calculated as approximately 11.55%.
Therefore, the NPV is -$37.65 and the IRR is approximately 11.55%.
To know more about NPV here
https://brainly.com/question/33284820
#SPJ11
A box can at most be packed with 50 eggs. If there are
currently 20 eggs already. How many eggs can be added at
most?
____ eggs
Answers
Answer:
30
Step-by-step explanation:
the standard deviation of the scores on a skill evaluation test is 421 points with a mean of 1728 points. if 309 tests are sampled, what is the probability that the mean of the sample would differ from the population mean by less than 36 points? round your answer to four decimal places.
Answers
The probability that the mean of the sample would differ from the population mean by less than 36 points is 0.0316
To calculate the probability that the mean of the sample would differ from the population mean by less than 36 points, we need to use the Central Limit Theorem.
The Central Limit Theorem states that for a large sample size, the sampling distribution of the sample mean will be approximately normally distributed, regardless of the shape of the population distribution.
Given:
Standard deviation (σ) = 421 points
Mean (μ) = 1728 points
Sample size (n) = 309 tests
To calculate the probability, we need to find the z-score associated with a difference of 36 points and then find the corresponding probability using the standard normal distribution table or a statistical calculator.
The formula for the z-score is:
z = (x - μ) / (σ / √n)
Plugging in the values:
z = (36 - 0) / (421 / √309)
Calculating the z-score:
z = 36 / (421 / √309)
z ≈ 2.1604
Now, we need to find the probability associated with this z-score. Looking up the z-score of 2.1604 in the standard normal distribution table, we find that the probability is approximately 0.9842.
However, we need to consider both tails of the distribution because we're looking for a difference in either direction (less than 36 points or greater than -36 points). Therefore, we need to find the area in both tails.
Since the standard normal distribution is symmetric, we can calculate the area in one tail and multiply it by 2 to get the total probability.
Area in one tail = 1 - 0.9842
Area in one tail ≈ 0.0158
Total probability = 2 * 0.0158
Total probability ≈ 0.0316
Rounding the answer to four decimal places, the probability that the mean of the sample would differ from the population mean by less than 36 points is approximately 0.0316.
Learn more about probability at https://brainly.com/question/15030736
#SPJ11
The names of the automobile manufacturer of the car that you drive is what type of variables ( scales of measurement)
Answers
The type of variable that represents the names of the automobile manufacturers would be the categorical variable.
What are variables in research work?A variable is defined as the quantity that may change within the context of a mathematical problem, research work or an experiment.
There are various types of variables that include the following:
categorical variables.Nominal variables. Ordinal variables. Numeric variables. Continuous variables. Discrete variables.Learn more about variables here:
https://brainly.com/question/30292654
#SPJ1
A survey of statistics undergraduate at prosperity university completed a survey that asked for their verbal and math sat scores. They wanted to predict the verbal score based on the math score. The value of r-squared was 12. 78%. The least squares regression equation is yhat = 383. 3 + 0. 3489x. Find r.
Answers
The coefficient of determination (r-squared) provides an indication of how well the regression model fits the data and the value of r is 0.3574
In this example, the r-squared value is 12.78%, which means that 12.78% of the variation in verbal SAT scores can be explained by the variation in math SAT scores. The least squares regression equation is yhat = 383.3 + 0.3489x, where yhat is the predicted verbal score and x is the math score.
The coefficient of correlation (r) provides a measure of the strength of the linear relationship between two variables. In this example, the coefficient of correlation (r) can be calculated from the coefficient of determination (r-squared) as follows: r = √r-squared = √12.78% = 0.3574. This indicates that there is a weak linear relationship between verbal and math SAT scores.
For more questions like R-squared click the link below:
https://brainly.com/question/13324767
#SPJ4
Factor each polynomial.
3 m²-9
Answers
On factorizing the polynomial 3m²-9 we get 3(m²-3).
The factor of polynomial is defined as the process of expressing the polynomial as a product of two or more polynomials.
For Example : the factors of x²-16 are (x+4)(x-4).
In the given question we need to factor
3m²-9
here 9 can be written as 3*3
rewriting the above equation we get
3m²-3*3
As both the terms contain 3 we can take 3 common from both the terms ;
taking 3 common from each term we get ,
=3(m²-3)
Therefore , On factorizing 3m²-9 we get 3(m²-3) .
Learn more about factorization here https://brainly.com/question/9177249
#SPJ1
Select the correct answer from each drop-down menu.

Answers
Step 1: Start by drawing a circle.
Step 2: On the circle, choose any point. Label its endpoints A and C.
Step 3: Set the width of the compass larger than the radius of the circle. Draw arcs centered at A and C on each side of the diameter.
Step 4: Connect the arcs and the center of the circle. Label the points of intersection with the circle as B and D.
Step 5: Draw chords AB, BC, CD, and DA.
What is a circle?A circle is a fundamental geometric shape in mathematics. It is a two-dimensional figure that consists of all points in a plane that are equidistant from a fixed point called the center. The distance from the center to any point on the circle is known as the radius.
A circle is defined by its center and radius. The center is usually represented by the coordinates (h, k), where 'h' represents the horizontal position and 'k' represents the vertical position. The radius is the distance between the center and any point on the circle.
learn more about a circle: https://brainly.com/question/14068861
#SPJ1
round 8,272 to the nearest thousand
Answers
Answer:
8000
Step-by-step explanation:
Answer: Therefore, the number 8272 rounded to the nearest thousand is 8000
Step-by-step explanation:
If there is a parametrized curve:
r(t)=t2i+ln(t)j+1tk
then as I understand it, to find surfaces that contain the curve, you can solve for t
and find three equations, each missing one of the three variables, giving three equations for surfaces that contain the curve.
x=t2y=ln(t)z=1t
1)t=1z⇒x=(1z)2=1z2
2)y=ln(t)⇒t=ey⇒x=e2y
3)z=1t=1ey
Above are three surfaces that contain the curve; but are there infinitely many surfaces that contain this curve? Could you not translate that surface infinitely many times and still have the curve lie on the surface?
Answers
Yes, there exist infinitely many surfaces that contain the given curve,\(`r(t) = t^2 i + ln(t) j + 1 tk`.\)
Given that \(`r(t) = t^2 i + ln(t) j + 1 tk`\).In order to find the surfaces that contain the curve, we can solve for 't' and get three equations, each missing one of the three variables, giving three equations for surfaces that contain the curve.
They are,\(x = t^2 (y = ln(t) and z = 1/t),\)
\(y = ln(t) (x = t^2 and z = 1/t)\)
\(z = 1/t (x = t^2 and y = ln(t)).\)
These three equations represent the surfaces that contain the curve. But, as you mentioned, there are infinitely many surfaces that contain the curve. This is because we can translate the surface infinitely many times and still have the curve lie on the surface.
For example, the surfaces of the form,x = t^2 + a,
y = ln(t) + b and
z = 1/t + c (a, b, c are constants) also contain the curve.
Hence, there exist infinitely many surfaces that contain the given curve, `r(t) = t^2 i + ln(t) j + 1 tk`.
To know more about infinitely visit:
https://brainly.com/question/32237150
#SPJ11
Estimate the area under the graph of f(x) =10 sqrt x from x = 0 to x = 4 using four approximating rectangles and right endpoints. (Round your answers to four decimal places.)
(a) Use four approximating rectangles and right endpoints.
R4=______________________
(b) Use four approximating rectangles and left endpoints.
L4=_______________________
Answers
(a) R4= 61.4626 and (b) L4= 61.4626.
In order to estimate the area under the graph of f(x) = 10 sqrt x from x = 0 to x = 4 using four approximating rectangles and right endpoints, we need to use the formula:
Rn = Δx [f(x1) + f(x2) + f(x3) + ... + f(xn)], where Δx is the width of each rectangle and f(xi) is the height of the rectangle at the right endpoint of the ith interval.
Step 1: Calculation of ∆x.∆x = (4 - 0)/4 = 1
Step 2: Calculation of xi for i = 1, 2, 3 and 4.x1 = 1, x2 = 2, x3 = 3, x4 = 4
Step 3: Calculation of f(xi) for i = 1, 2, 3 and 4.f(x1) = 10√(1) = 10f(x2) = 10√(2) ≈ 14.1421f(x3) = 10√(3) ≈ 17.3205f(x4) = 10√(4) = 20
Step 4: Calculation of R4.R4= ∆x [f(x1) + f(x2) + f(x3) + f(x4)]R4= 1[10 + 14.1421 + 17.3205 + 20]= 61.4626Area ≈ 61.4626 square units.
Step 5: Calculation of L4.Ln = ∆x [f(x0) + f(x1) + f(x2) + ... + f(xn-1)]
Where x0 is the initial value.
Here, we can find the value of L4 by using the left endpoints.
So, x0 = 0L4 = ∆x [f(x0) + f(x1) + f(x2) + f(x3)]L4 = 1 [f(0) + f(1) + f(2) + f(3)]L4 = 1 [10 + 14.1421 + 17.3205 + 20]L4 = 61.4626
Therefore, (a) R4= 61.4626 and (b) L4= 61.4626.
Know more about rectangles here,
https://brainly.com/question/29123947
#SPJ11
how do I do this problem I'm doing test corrections and I have no idea how to do it

Answers
Answer:
i think its 3 but dont quote me
Step-by-step explanation:
Answer:
B
Step-by-step explanation:
9 can help in completing square formula
The boss told the management team some sad news too. “I’m cutting your hourly pay. You now get paid per project you finish. I will give you $10 for each finished schedule you create and $20 for each meeting you complete! You cannot make more than $100 per day! Also you must make more than twice as many schedules as meetings!”
Create a system of linear inequalities to model the situation above, where x is the number of schedules made and y is the number of meetings completed.
Answers
The system of linear inequalities to model the situation is 10x + 20y ≤ 100 and y > 2x
How to create a system of linear inequalities to model the situationFrom the question, we have the following parameters that can be used in our computation:
Each finished schedule = $10Each meeting = $20Amount to make = Not more than $100You must make more than twice as many schedules as meetingsUsing the following representations:
x = the number of schedules madey = the number of meetings completedWe have the following system of inequalities from the given statements
10x + 20y ≤ 100
y > 2x
Hence, the system of inequalities is 10x + 20y ≤ 100 and y > 2x
Read more about system of inequalities at
https://brainly.com/question/4180576
#SPJ1
A function p(x) is shown on the graph below.
O True
O False

Answers
Answer:
True
Step-by-step explanation:
The point \((0,3)\) lies on the graph.
6 – k, for k = -67 i need a sentence
Answers
Answer:
6-(-67) = 73
Step-by-step explanation:
If k equals -67 the answer would be 73.
if 0 < 0 < pi/2, as 0 increases, the value of cos0 and the value of sin0
Answers
As the angle increases from 0 to π/2, the value of sine increases, and the value of cosine decreases.
Trigonometry is a branch of mathematics that deals with the relationships between angles and sides of triangles.
Let us first understand the concept of sine and cosine. In a right-angled triangle, the sine of an angle is defined as the ratio of the length of the side opposite to the angle and the length of the hypotenuse. Similarly, the cosine of an angle is defined as the ratio of the length of the adjacent side and the length of the hypotenuse.
As the angle θ increases from 0 to π/2, the length of the opposite side (the numerator in sine) of the triangle increases, and the length of the hypotenuse (the denominator in sine) remains the same. Therefore, the value of sine increases as θ increases.
On the other hand, as the angle θ increases from 0 to π/2, the length of the adjacent side (the numerator in cosine) decreases and the length of the hypotenuse (the denominator in cosine) remains the same. Therefore, the value of cosine decreases as θ increases.
This behavior is consistent with the fact that sine is an increasing function, while cosine is a decreasing function within this range of angles.
To know more about trignonmentry here.
https://brainly.com/question/22986150
#SPJ4
Complete Question:
If 0< θ <π/2, as Theta increases, the value of
cos(θ) [Decreases/Increases/Remains The Same]
and the value of sin(θ) [Decreases/Increases Remains The Same]
find the measure of angle b. (alternate exterior = 134 degrees)

Answers
Answer:
b=59
Step-by-step explanation:
The Theorem for Alternate Exterior angles is: If two parallel lines are cut by a transversal then the alternate exterior angles are congruent.
By this theorem we now know that b=59 degrees.
Please help. First correct answer gets brainliest.
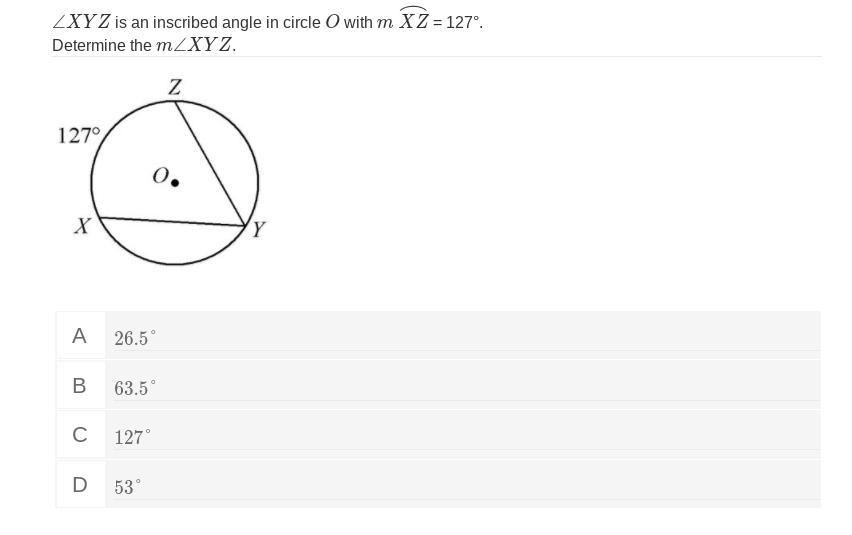
Answers
Answer:
63.5°
Step-by-step explanation:
By inscribed angle theorem:
\( m\angle XYZ=\frac{1}{2} \times m\widehat {XZ} \)
\( \therefore m\angle XYZ=\frac{1}{2} \times 127\degree \)
\( \therefore m\angle XYZ=63.5\degree \)
2
Select the correct answer.
A community center has an L-shaped swimming pool that is 10 feet deep. What is the volume of the pool?
10 ft.
6 ft.
20 ft.
16 ft.
10 ft.
Answers
The volume of the pool, if The depth of the pool is 10 feet, is 1040 cubic feet.
What is volume?The capacity occupied by a three-dimensional solid shape is known as volume. It is difficult to visualize in any shape, yet it may be compared among shapes. For instance, a compass box has a larger volume than an eraser placed inside of it.
Given:
The depth of the pool is 10 feet,
Calculate the volume of the pool as shown below,
The volume of the pool = the Volume of a rectangular prism with dimensions 20ft. × 10ft. × 4ft. + volume of a rectangular prism has dimensions: 6ft. × 4ft. × 10ft.
The volume of the pool = 20 × 10 × 4 + 6 × 4 × 10
The volume of the pool = 200 × 4 + 24 × 10
The volume of the pool = 800 + 240
The volume of the pool = 1040
Thus, the volume of the pool is 1040 ft³.
To know more about volume:
brainly.com/question/13807002
#SPJ1
please help ill mark brainliest and add explanation too pleas

Answers
Step-by-step explanation:
In A,
length=3units
width=2 units
area=length×width
area=3×2 sq.units
area=6 sq.units
In B,
length=1unit
width=4units
area=length × width
area=1unit × 4units
area= 4 sq.units
Note:if you need to ask any question please let me know.
Find the slope of the line between the points (0, -4) and (2, 8).
Answers
Answer: The slope is 6.