12 Work out an expression for the nth term for each sequence.b,20,19.8,19.6,19.4
Answers
Answer:
18.2
Step-by-step explanation:
20 + (n-1)-.2
n is the number of the term.
-.2 is the common difference
20 + (10-1) -.2
20 + 9(-.2)
20 - 1.8
18.2
Related Questions
(Pic) How many tablets, please help!
Show steps please

Answers
The number of tablets that should be taken each day by the patient who needs Synthroid is 1 tablet.
How to find the number of tablets ?To find the number of tablets of Synthroid that should be taken, you convert the requirements from micrograms ( μg ) to milligrams ( mg).
1 milligram = 1, 000 micrograms ( μg )
25. 0 μg in milligrams is therefore:
= 25 / 1, 000
= 0. 025 mg
This means that the number of tablet to take is:
= Mg requirement / Mg of tablet
= 0. 025 / 0. 025
= 1 tablet
Find out more on tablets at https://brainly.com/question/11217552
#SPJ1
find p80, the 80th percentile for the red blood cell counts for women
Answers
The 80th percentile is also known as the upper quartile. To find the 80th percentile for a set of data, you need to first arrange the data in numerical order. The 80th percentile is the value below which 80% of the data falls.
The required details for upper quartile in given paragraph
For example, if you have a set of red blood cell counts for women as follows:
3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4.0, 4.1, 4.2, 4.3
You can arrange the data in numerical order as follows:
3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4.0, 4.1, 4.2, 4.3
To find the 80th percentile, you need to find the value below which 80% of the data falls. In this case, 80% of the data is 8 values, so the 80th percentile is the 8th value in the list, which is 4.1.
Therefore, the 80th percentile for the red blood cell counts for women in this example is 4.1.
The 50th percentile, or median, is the value that divides the data into two equal parts. The 20th percentile, or lower quartile, is the value below which 20% of the data falls.
To know about upper quartile click here
https://brainly.com/question/10353201
#SPJ1
K
A golf ball is hit with an initial velocity of 140 feet per second at an inclination of 45° to the horizontal In physics, it is established that the height h of the golf ball is given by the function
- 32x²
h(x)=-
140²
where x is the horizontal distance that the golf ball has traveled Complete parts (a) through (g)
(a) Determine the height of the golf ball after it has traveled 100 feet
h= feet (Round to two decimal places as needed)
Answers
Answer:
6.25 seconds
Step-by-step explanation:
Using the the equation
h = 100t − 16t^2
The ball hits the ground, when h = 0, solving below equation:
100t − 16t^2 = 0
4t(25 - 4t) = 0
t = 0 seconds, this is the starting point when ball was hit
25 - 4t = 0 ⇒ 4t = 25 ⇒ t= 25/4 = 6.25 seconds later the ball hits the ground
10x+8 = 11x -8
Solve for x.
Answers
Answer:
x = 16
Step-by-step explanation:
We are given the equation:
\( \displaystyle \large{10x + 8 = 11x - 8}\)
First, subtract both sides by 10x.
\( \displaystyle \large{10x - 10x+ 8 = 11x - 10x - 8} \\ \displaystyle \large{8= x- 8}\)
Then add both sides by 8 to isolate x-term.
\( \displaystyle \large{8 + 8= x- 8 + 8} \\ \displaystyle \large{16 = x}\)
And we're done! The value of x is 16.
what is the equation for 30 out of 3/6,I’m doing a tape diagram!!

Answers
Out of the 30, 15 students brought snacks
From the question, we have it that out of the 30 students, only 3/6 bought
The number that brought snacks can be calculated by multiplying the fraction with the number of students
Mathematically, we have this as;
\(\frac{3}{6}\times30\text{ = 15}\)Iris is a working freelancer and has been tracking her monthly income for the last four months she found out that she made $2700 $4600 $3550 and $1700 when making her budget what income value should she use
Answers
Iris should use an income value of approximately $3,137.50 when making her budget.
When making her budget as a freelancer, Iris should use an income value that reflects her average earnings over the past four months. By calculating the average income, Iris can have a more stable and reliable estimate for her budget planning.
To determine the average income, Iris needs to add up the total income earned over the four months and divide it by the number of months. Summing up the income values, we get:
$2700 + $4600 + $3550 + $1700 = $12,550
Next, dividing the total income by four (the number of months), we find:
$12,550 / 4 = $3,137.50
Therefore, Iris should use an income value of approximately $3,137.50 when making her budget. This average value allows her to account for fluctuations in her monthly income and provides a more accurate representation of her earning potential.
It is important for Iris to consider her expenses and financial goals when budgeting. By using the average income, she can create a budget that balances her income and expenses, allowing her to allocate funds appropriately for various needs such as bills, savings, investments, and personal expenses.
For more such questions on value,click on
https://brainly.com/question/843074
#SPJ8
The probable question may be:
Iris is a working freelancer and has been tracking her monthly income for the last four months, which are $2700, $4600, $3550, and $1700. What income value should she use when making her budget?
1.
7844
A
27
B
26.4
2.
1900
C.
29.1
3.
1650
D.
28,4
4
1784
E
28
F.
26.1
5,
1699
G
25.5
6.
V805
H
30
7
1729
Answers
Answer:
gebiz hadi bir ben kusura siz
Step-by-step explanation:
sneidmd
Geometry Help!
Please only answer if you know the answer. Look at the image below to answer the question.
Be sure to show all of your work and explain your thinking.
I posted 3 of these, so if you understand it, please go and check them out.
If you do not know the answer use the comment section, don't answer my question with a comment. Thanks, Good Luck!

Answers
Answer:
x = 8.8Step-by-step explanation:
To solve this you need the Law of sines
sin A / a = sin B / b = sin C / ca, b, c are the sides opposite to angles A, B and C respectively
Applied to the given triangle we have one side given, the opposite angle to be found.
sin 28 / x = sin (180 - 28 - 126) / 8.2sin 28 / x = sin 26 / 8.2x = 8.2 sin 28 / sin 26x = 8.8 (rounded)Which expression represents a cube root of 1 + i?
OVE (cos()+ i sin (24))
OVE (cos (37) + i sin (3))
/
O & (cos (4) + i sin (24))
V2 (cos (37) + 1 sin (37))

Answers
Answer:c
Step-by-step explanation is va cuz when your multiply:
Answer:
\(\sqrt[6]{2}\left(\cos\left(\frac{3\pi}{4}\right)+i\sin\left(\frac{3\pi}{4}\right)\right)\)
Step-by-step explanation:
The analysis is as attached below.

Which of the following cities does NOT rely on lumber for its economy?
Answers
Describe the transformation.y = - [xl-5reflect over x-axis, vertical compress by factor of 3, and shift down 5reflect over x-axis, vertical compress by factor of 3, and shift up 5reflect over x-axis, vertical stretch by factor of 2, and shift down5reflect over x-axis, vertical stretch by factor of 2, and shift up 5
Answers
we have the equation
\(y=-\frac{1}{3}\mleft|x\mright|-5\)the parent function is
\(y=\mleft|x\mright|\)so
the transformations of the parent function to the given equation are
1) Reflection over x-axis
the rule is
(x,y) -------> (x,-y)
so
\(\mleft|x\mright|---\longrightarrow\text{ -}\mleft|x\mright|\)2) vertical compress by factor of 3
\(-|x|---\longrightarrow\text{ -}\frac{1}{3}|x|\)3) shift down 5
\(\text{-}\frac{1}{3}|x|---\longrightarrow\text{ -}\frac{1}{3}|x|-5\)therefore
the answer is
reflect over x-axis, vertical compress by factor of 3, and shift down 5how to solve this separable differential equation?

Answers
The solution to the differential equation \(2^{\sqrt{x}}\frac{dy}{dx} = cosce(ln(y))\) is,
\(\frac{y sin(ln(y))}{2} - \frac{y cos(ln(y))}{2} = C - \frac{2 ln(2) \sqrt{x} + 2}{ln^2(2)2^{\sqrt{x}}}\).
What is a differential equation?Any equation with at least one ordinary or partial derivative of an unknown function is referred to as a differential equation.
The given differential equation is \(2^{\sqrt{x}}\frac{dy}{dx} = cosce(ln(y))\).
Now, multiplying both sides by dx we,
\(2^{\sqrt{x}}dy = cosce(ln(y))dx\).
Dividing both sides by \(2^{\sqrt{x}}\) we have,
\(sin(ln(y))dy = \frac{dx}{2^{\sqrt{x}}}\).
\(\[ \int sin(ln(y))dy = \int \frac{dx}{2^{\sqrt{x}}}\).
\(\frac{y sin(ln(y))}{2} - \frac{y cos(ln(y))}{2} = C - \frac{2 ln(2) \sqrt{x} + 2}{ln^2(2)2^{\sqrt{x}}}\).
learn more about differential equations here :
https://brainly.com/question/14620493
#SPJ9
Anyone could help out with this

Answers
Answer:
C
Step-by-step explanation:
The answer is the orange one because pie * radius^2 leads to the area of the circl.e
A rectangular room is 1.3 times as long as it is wide, and its perimeter is 27 meters. Find the dimension of the room.
Answers
The dimensions of the room are approximately 5.87 meters by 7.63 meters.
Let's assume the width of the room is "x" meters.
According to the problem, the length of the room is 1.3 times the width, so the length would be 1.3x meters.
The perimeter of a rectangle is calculated by adding the lengths of all four sides. In this case, the perimeter is given as 27 meters.
Perimeter = 2(length + width)
Substituting the values we know:
27 = 2(1.3x + x)
Simplifying:
27 = 2(2.3x)
27 = 4.6x
Dividing both sides by 4.6:
x = 27 / 4.6
x ≈ 5.87
The width of the room is approximately 5.87 meters.
To find the length, we can multiply the width by 1.3:
Length = 1.3 * 5.87 ≈ 7.63
The length of the room is approximately 7.63 meters.
Therefore, the dimensions of the room are approximately 5.87 meters by 7.63 meters.
For more such questions dimensions,click on
https://brainly.com/question/28107004
#SPJ8
16 families went on a trip which cost them Rs 2,16,352. How much did each
family pay?
Answers
Given that 16 families went on a trip and the cost of the trip was Rs. 2,16,352.The amount paid by each family is to be determined by unitary method Hence each family paid Rs.13522
Now, let's solve this by using the method of unitary method. To find the cost of 1 family trip, we will divide the total cost of the trip by the number of families.2,16,352 / 16 = 13,522 So, the cost of the trip per family is Rs. 13,522.Hence, each family paid Rs. 13,522 for the trip.
to know more about unitary method
https://brainly.com/question/28276953
Answer:
Step-by-step explanation
1. The total cost of the trip for all 16 families is Rs 2,16,352.
2. To find out how much each family paid, we need to divide the total cost by the number of families: Rs 2,16,352 ÷ 16.
3. When we do the division, we get the result: Rs 13,522.
Now let's check if this result is correct:
1. If each family paid Rs 13,522 for the trip, then the total cost for all 16 families would be: 16 × Rs 13,522 = Rs 2,16,352.
2. This is exactly the same as the total cost given in the problem statement.
So we have shown that each family paid **Rs 13,522** for the trip
6 bags of coins each contain 10 nickels and the same number of pennies. Altogether, the bags contain 180 coins. Write and solve an equation to find the number of pennies in each bag.
Answers
Each bag contains 20 pennies and we have 6 such bags.
What is a numerical expression?A numerical expression is a mathematical statement written in the form of numbers and unknown variables. We can form numerical expressions from statements.
From the given information let the number of pennies in each bag is 'x'
and we have 6 such bags.
Therefore, The equation can be formed as,
6(10 + x) = 180.
60 + 6x = 180.
6x = 180 - 60.
6x = 120.
x = 120/6.
x = 20.
So, The number of pennies in each bag is 20.
learn more about numerical expressions here :
https://brainly.com/question/29199574
#SPJ9
The Acme Company manufactures widgets. The distribution of widget weights is bell-shaped. The widgetweights have a mean of 58 ounces and a standard deviation of 9 ounces.Use the Standard Deviation Rule, also known as the Empirical Rule.Suggestion: sketch the distribution in order to answer these questions.oz anda) 99.7% of the widget weights lie betweenOZfonyb) What percentage of the widget weights lie between 40 and 85 ounces?%c) What percentage of the widget weights lie below 67 ?%Question Help: D VideoSubmit Question
Answers
SOLUTION
The empirical rule, also referred to as the three-sigma rule or 68-95-99.7 rule, is a statistical rule which states that for a normal distribution, almost all observed data will fall within three standard deviations (denoted by σ) of the mean or average (denoted by µ).
In particular, the empirical rule predicts that 68% of observations falls within the first standard deviation (µ ± σ), 95% within the first two standard deviations (µ ± 2σ), and 99.7% within the first three standard deviations (µ ± 3σ).
The image below shows a sketch of the distribution following the empirical rule
a) 99.7% of the widget lies between 3 standard deviations to the right and left of the mean.
\(\begin{gathered} 58+3(9)=85oz_{} \\ 58-3(9)=31oz \end{gathered}\)99.7% of the widget lies between 31 oz and 85 oz.
b) The percentage of the widget weights that lies between 40 and 85 ounces is calculated thus:
\(49.85+47.5=\text{ 97.35}\)The answer is 97.35%
c)
\(\begin{gathered} 100-16 \\ =84 \end{gathered}\)The answer is 84%

Write the given statement using symbols type any Quetion do not simplify The sum of X and eight is the product of seven and 10
Answers
Answer:
\(x+8=7*10\)
Step-by-step explanation:
Sum of X and 8: \(x+8\)
Product of seven and 10: \(7*10\)
Put them together:
\(x+8=7*10\)
What is the following product 3/x^2 4/x^3??
Answers
9514 1404 393
Answer:
12/x^5
Step-by-step explanation:
The fractions are multiplied in the usual way. The applicable rule of exponents is ...
(x^a)(x^b) = x^(a+b)
__
\(\dfrac{3}{x^2}\cdot\dfrac{4}{x^3}=\dfrac{3\cdot4}{x^2\cdot x^3}=\dfrac{12}{x^{2+3}}=\boxed{\dfrac{12}{x^5}}\)
The vertices of triangle ABC are given: A (0;-1) B(12; -10) C(10;4)
Find:
a) the equation of the median and bisector drawn from vertex A;
b) the equation of the altitude from vertex B;
c) the point of intersection of the median and height;
d) the coordinates of the center of mass (the point of intersection of the medians).
Answers
verified
Verified by Toppr
Median bisects the line.
D≡(
2
−3+5
,
2
−9−8
)≡(1,
2
−17
)
E≡(−
2
1+5
,
2
6−8
)≡(2,−1)
F≡(−
2
1−3
,
2
6−9
)≡(−2,
2
−3
)
∴ equation of AD:(y−y
1
)=(
x
2
−x
1
y
2
−y
1
)
AD
(x−x
1
)
⇒(y−6)=
⎝
⎜
⎜
⎛
1+1
2
−17
−6
⎠
⎟
⎟
⎞
(x+1)⇒(y−6)=−
4
29
(x+1)
⇒
4
29
x+y−6+
4
29
=0
AD⇒29x+4y+5=0
equation of BE:(y+9)=(−
2+3
1+9
)
BE
(x+3)
⇒(y+9)=
5
8
(x+3)⇒5y+45=8x+24
BE⇒8x−5y−21=0
Equation of CF:(y+8)=
⎝
⎜
⎜
⎛
−2−5
−
2
3
+8
⎠
⎟
⎟
⎞
CF
(x−5)
⇒(y+8)=−
14
13
(x−5)⇒14y+112=−13x+65
CF:13x+14y+47=0
Write (-4x^2ya^3)^2 as a monomial in standard form.
Answers
Answer:
\(16a^6x^4y^2\)
Step-by-step explanation:
To simplify this expression, use the exponent rule stating that when an exponent is put to an exponent, the exponent values are multiplied (e.g., \((x^2)^2 = x^{2 \cdot 2} = x^4\))
Using that rule, we get:
\((-4x^2ya^3)^2 = (-4)^2 \cdot x^{(2 \, \cdot \, 2)} \cdot y^2 \cdot a^{(3 \, \cdot \, 2)}\).
This can be simplified to
\(16 \cdot x^4 \cdot y^2 \cdot a^6\),
which can be written as:
\(16a^6x^4y^2\)
using the commutative property of multiplication.
If 2x-y=9 and 3x+4y=19, then y=
Answers
Answer:
x = 5
y = 1
Step-by-step explanation:
2x - y = 9
3x + 4y = 19
We multiply the first equation by 4
8x - 4y = 36
3x + 4y = 19
11x = 55
x = 5
Now we put 5 in for x and solve for y
2(5) - y = 9
10 - y = 9
-y = -1
y = 1
Let's Check the answer
2(5) - 1 = 9
10 - 1 = 9
9 = 9
So, x = 5 and y = 1 is the correct answer.
2. Which system has an infinite number of solutions?
a. x+2=y
4= 2y-x
b. 2y + 6 = 4x
-3=y-2x
c. y+3=2x
4x=2y-3
d. y = 2x - 5
-2 = y - 2x
Answers
Answer: B
Step-by-step explanation:
Substitution method
solve the equation for Y by putting the variable on the left. -3 = y - 2x would become y = 2x - 3
Plug Y into the top equation. 2(2x - 3) + 6 =4x
4x - 6 + 6 = 4x
Combine like terms
4x - 0 = 4x
4x = 4x
Infinite Solutions
All the edges of a regular square pyramid have length 8.
A) What is the volume of the pyramid?
B) What is the lateral area of the pyramid?
C) What is the total surface area of the pyramid?
Answers
Answer:
A) (256/3)√2 ≈ 120.68 units³
B) 64√3 ≈ 110.85 units²
C 64(1+√3) ≈ 174.85 units²
Step-by-step explanation:
The dimensions used in the usual formulas for area and volume are not given, so it can work reasonably well to start by finding them.
Each face is an equilateral triangle with side length 8, so the slant height is the altitude of that triangle: 8(√3/2) = 4√3.
The height of the pyramid is the vertical leg of a right triangle with hypotenuse equal to the slant height (4√3) and horizontal leg equal to half the base side length. The height is found from the Pythagorean theorem:
a² +b² = c²
b = √(c² -a²) = √((4√3)² -4²) = 4√2
The pyramid with all sides of length 8 has height 4√2 and slant height 4√3.
__
A)The volume is ...
V = 1/3s²h . . . . . . where s is the side length, and h is the height
V = 1/3(8²)(4√2) = (256/3)√2 ≈ 120.68 . . . . cubic units
__
B)The lateral area is the total area of the 4 triangular faces, so is ...
LA = 4(1/2)(bh) = 2(8)(4√3) = 64√3 ≈ 110.85 . . . . square units
h is the slant height in this formula
__
C)The total surface area is the sum of the base area and the lateral area. The base area is the square of the side length.
SA = 8² +64√3 = 64(1+√3) ≈ 174.85 . . . . square units
wondering if i could get help on the problem as soon as possible in the picture attached above

Answers
Given:
Given a figure.
Required: Area of the shaded figure
Explanation:
The shaded figure can be split into two: a rectangle, triangle
The area of the shaded region is the sum of thH area of the triangleeand the area of the rectangie.
First, find the areg of thh triangle.
t of the triangle = 2 units
Base ength of te triangle = 8 units
Area of th triangle
\(\begin{gathered} =\frac{1}{2}bh \\ =\frac{1}{2}\times8\times2 \\ =8\text{ units}^2 \end{gathered}\)Find the area of the rectangle.
Length of the rectangle = 4 units
Width of the rectangle = 6 units
Area of thereactanle
\(undefined\)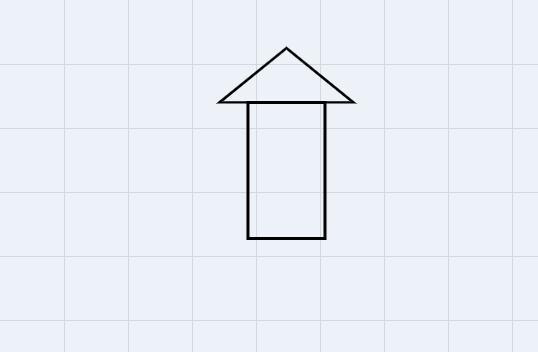
Hector is taking surfing classes with a surfing instructor. He has to pay a surf board rental fee and a fee per-hour that he works with the instructor. He has a coupon for a certain percent off the total cost. The expression (1−x)(125+80y) represents his cost after the coupon.
Answers
The expression (1 - x)(125 + 80y) gives us the final cost for Hector after applying the coupon, taking into account the surfboard rental fee and the fee per hour for the surfing classes with the instructor.
(1 - x): This represents the remaining percentage after applying the coupon. If the coupon offers a discount of x percent, then (1 - x) represents the percentage of the total cost that Hector has to pay.
(125 + 80y): This represents the original cost without any discounts or coupons. The term 125 represents the surfboard rental fee, and 80y represents the fee per hour that Hector works with the instructor (where y is the number of hours).
(1 - x)(125 + 80y): Multiplying the two terms together gives us the cost after applying the coupon. The expression (1 - x)(125 + 80y) represents the product of the remaining percentage after the coupon and the original cost.
Therefore, the expression (1 - x)(125 + 80y) gives us the final cost for Hector after applying the coupon, taking into account the surfboard rental fee and the fee per hour for the surfing classes with the instructor.
for such more question on percentage
https://brainly.com/question/24877689
#SPJ8
A library spent 5/8 of its budget to buy new books. They set aside 1/12 of the book money to buy young adult novels. What part of the budget went towards buying young adult novels?
Answers
Answer:
5/96
Step-by-step explanation:
Fraction used to buy new books = 5/8
Amount for book money = 1/12 of amount of adult novels
Part used for adult movies = 1/12 * 5/8
Part used for adult movies = 5/96
Hence the part of the budget that went towards buying young adult novels is 5/96
como resolver:
"los ceros son 0, -1, 1, 3/2, P(-3) = 300"
Answers
The polynomial with the given zeros is:;
P(x) = (300/108)*x*(x + 1)*(x - 1)*(x - 3/2)
How to find the polynomial?Remember that if a polynomial has the zeros a, b, c, and d, then we can write it as:
P(x) = K*(x - a)*(x - b)*(x - c)*(x - d)
Where K is a coefficient.
Here the zeros are 0, -1, 1, 3/2
Then we can write:
P(x) =K*(x - 0)*(x + 1)*(x - 1)*(x - 3/2)
P(x) =K*x*(x + 1)*(x - 1)*(x - 3/2)
We also know that when x = -3, P(x) = 300
Then we can write:
300 = K*(-3)*(-3 + 1)*(-3 - 1)*(-3 - 3/2)
300 = K*(-3)*(-2)*(-4)*(-9/2)
300 = K*108
300/108 = K
Then the polynomial is:
P(x) = (300/108)*x*(x + 1)*(x - 1)*(x - 3/2)
Learn more about polynomials at:
https://brainly.com/question/4142886
#SPJ1
FIND THE AREA OF THR FIGURE!
WILL MARK BRAINLIEST IF CORRECT!
I HAVE 5 MINS PLS HURRY

Answers
Answer:
231.04
Step-by-step explanation:
Answer:
229.14
Step-by-step explanation:
Multiply 7.5 by 19 for the area of the rectangle.This gets you 142.5.The area of the triangle is 86.64.Now add them together.If I am incorrect in my reasoning, please let me know so that I can plan better for my future answers. Have an amazing day.
. (-6, -5) and (2, 0) find the distance between each pair of points
Answers
The distance between the pair of points (-6, -5) and (2, 0) is √89.
To find the distance between the two points (x₁, y₁) and (x₂, y₂), we use the distance formula, according to which the distance d is shown as:
d = √((x₂ - x₁)² + (y₂ - y₁)²).
In the question, we are asked to find the distance between the pair of points (-6, -5) and (2, 0).
We take (x₁, y₁) = (-6, -5), and (x₂, y₂) = (2, 0).
Using the distance formula,
d = √((x₂ - x₁)² + (y₂ - y₁)²),
and substituting the values of x₁, y₁, x₂, and y₂, we get:
d = √((2 - (-6))² + (0 - (-5))²),
or, d = √((2 + 6)² + (0 + 5)²),
or, d = √(8² + 5²),
or, d = √(64 + 25),
or, d = √89.
Thus, the distance between the pair of points (-6, -5) and (2, 0) is √89.
Learn more about the distance formula at
https://brainly.com/question/17273444
#SPJ9