12 x 3.4x - 5.4x - x
Answers
Answer:
34.4x
Step-by-step explanation:
Answer:
34.4x
Step-by-step explanation:
40.8x-6.4x=34.4x
Related Questions
Which expression has a solution of 56 if r = 8?
8r
7r
6 r
9 r
Answers
Answer:
7r is the correct answer
Step-by-step explanation:
7 x 8 = 56
WILL GIVE BRAINLIST TO BEST ANSWER
find the value of x
14 and 12

Answers
14 ) x + 37 + 37 = 180
or , x + 74 = 180
or , x = 180 - 74
or , x = 106
Please only answer if you have a serious answer not just “do your work” I’m in 18 classes and my school won’t let me out of any of them. I’m just really confused so any help would be nice!
Write your own quadratic equation in standard form. Convert this quadratic to factored form. Be sure to show all of your work. Post to the discussion board these two equations and the work you did to convert from quadratic form to standard form.
Now write a new, different quadratic function, f of x, in standard form. Convert this quadratic function to factored form. Post to the discussion board both of these functions and the work you completed to convert from the quadratic form of the function to the factored form of the function.
Use your factored equation and your factored function to explain the differences between roots, x-intercepts, zeros, and solutions.
Answers
9514 1404 393
Explanation:
1) 2x^2 -5x -3 = 0 . . . . standard form equation
To convert this to factored form, you can look for factors of the product (2)(-3) that have a sum of -5. It can help to start by listing the ways that -6 can be factored. Since we want the sum of factors to be negative, we want to have larger negative factors.
-6 = (1)(-6) = (2)(-3)
The sums of these factor pairs are -5 (what we want) and -1 (not relevant). We can call these factors p=1 and q=-6.
If a = 2 is the leading coefficient of our standard form quadratic, we want to use these factors in the form ...
(ax +p)(ax +q)/a . . . . . factored form of the quadratic
(2x +1)(2x +(-6))/2 . . . .fill in the values we know
(2x +1)(x -3) . . . . . . . factor 2 from the second binomial
So, the factored form of the quadratic equation is ...
(2x +1)(x -3) = 0 . . . . factored form equation
__
2) f(x) = x^2 +7x +10 . . . . standard form quadratic function
Using the thinking process described above, we are looking for factors of 10 that have a sum of 7. We know those are 2 and 5. So, the factored form of the function is ...
f(x) = (x +2)(x +5) . . . . . . factored form quadratic function
The leading coefficient is 1, so we have no further work to do.
Roots, x-intercepts, zeros
The graph attached below shows this function crosses the x-axis when x=-2 and x = -5. These values of x are variously called "roots", "x-intercepts", and "zeros" of the function. They are values for which the factors and the function are zero. (x+2=0 when x=-2, for example)
Solutions
Often, we are interested in solving the equation ...
f(x) = 0
For that equation, the solutions are the zeros or x-intercepts or roots. The graph attached also shows solutions for ...
f(x) = 4
Those solutions are x = -6 and x = -1. The function value is not zero for these values of x, so the roots, x-intercepts, or zeros are not solutions to this equation.

a tank contains 240 liters of fluid in which 50 grams of salt is dissolved. pure water is then pumped into the tank at a rate of 6 l/min; the well-mixed solution is pumped out at the same rate. find the number
Answers
The tank contains 240 liters of fluid in which 50 grams of salt is dissolved. pure water is then pumped into the tank at a rate of 6 l/min; the well-mixed solution is pumped out at the same rate, After 20 minutes, the amount of salt in the tank is still 50 grams.
In order To calculate the amount of salt in the tank after 20 minutes, we basically use the formula: Salt (in grams) = (Amount of salt in the tank x Time) / Total volume.So, after 20 minutes, the amount of salt in the tank is: (50 grams x 20 minutes) / 240 liters = 8.33 grams.
As we can see, both methods produce the same result, confirming that the amount of salt in the tank after 20 minutes is still 50 grams. since the rate of pumping in salt water is equal to the rate of pumping out salt water, so the total amount of salt remains the same.
To know more about pump refer to the link brainly.com/question/21864603
#SPJ4
A tank contains 240 liters of fluid in which 50 grams of salt is dissolved. pure water is then pumped into the tank at a rate of 6 l/min; the well-mixed solution is pumped out at the same rate. find the number of grams of salt in the tank after 20 minutes
Boden's account has a principal of $800 and a simple interest rate of %3.2 Complete the number line. How much money will be in the account after 4 years, assuming Boden does not add or take out any money?
Answers
Answer:
The simple interest is calculated by multiplying the principal amount by the interest rate and the number of years.
Simple Interest = Principal x Interest Rate x Time
The simple interest on Boden's account is:
800 x 3.2% x 4 = 800 x 0.032 x 4 = $256
To find the total amount in the account after 4 years, we add the interest to the principal:
800 + 256 = $1056
So, Boden's account will have $1056 after 4 years.
On a merry-go-round, you stand 15 feet from the center while your friend stands 10 feet from the center. How would you find how much further you travel in one revolution than your friend? What is that distance?
Answers
Answer:
Revolution traveled by me = 30π ft.
Revolution traveled by my friend = 20π ft.
Difference between revolutions = 10π ft.
Step-by-step explanation:
In one revolution, I travel 2π(15) = 30π ft., and my friend travels 2π(10) = 20π ft., so my revolution is 30π - 20π, or 10π, ft. longer than my friend's revolution.
2.1Simplifying Expressions: Problem 1 (1 point) Simplify the following expression. 6- 4(x - 5)-
Answers
The simplified expression is 26 - 4x.
To simplify the expression 6 - 4(x - 5), we can apply the distributive property and simplify the terms.
6 - 4(x - 5)
First, distribute -4 to the terms inside the parentheses:
6 - 4x + 20
Now, combine like terms:
(6 + 20) - 4x
Simplifying further:
26 - 4x
Therefore, the simplified expression is 26 - 4x.
Learn more about distributive property here
https://brainly.com/question/12192455
#SPJ11
I don't know what it so to help 3/4-2/5
Answers
Answer:
Your answer would be 7/20 or 0.35.
Suppose that 8∫3 f(x)dx=6 and 8∫3 g(x)dx=-2 Which of the following is NOT necessarily true?

Answers
The correct derivative expressions of the given ones are -
\($1.\;\;\int\limits^3_3 {f^{2} (x)} \, dx = 0\)
\($2.\;\int\limits^3_8 {g(x)-f(x)} \, dx =\)\($\int\limits^3_8 {g(x)} \, dx - \int\limits^3_8 {f(x)} \, dx = -2 - 6 = -8\)
\($3.\;\;\int\limits^3_8 {4f(x)} \, dx - \int\limits^3_8 {2g(x)} \, dx = 24 - 4 = 20\)
What are algebraic expressions?In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context.Mathematical symbols can designate numbers (constants), variables, operations, functions, brackets, punctuation, and grouping to help determine order of operations and other aspects of logical syntax.It is given that -
\($\int\limits^3_8 {f(x)} \, dx = 6\\\)
and
\($\int\limits^3_8 {g(x)} \, dx\)
The correct statements of the given are -
\($1.\;\;\int\limits^3_3 {f^{2} (x)} \, dx = 0\)
\($2.\;\int\limits^3_8 {g(x)-f(x)} \, dx =\)\($\int\limits^3_8 {g(x)} \, dx - \int\limits^3_8 {f(x)} \, dx = -2 - 6 = -8\)
\($3.\;\;\int\limits^3_8 {4f(x)} \, dx - \int\limits^3_8 {2g(x)} \, dx = 24 - 4 = 20\)
Therefore, the correct derivative expressions of the given ones are -
\($1.\;\;\int\limits^3_3 {f^{2} (x)} \, dx = 0\)
\($2.\;\int\limits^3_8 {g(x)-f(x)} \, dx =\)\($\int\limits^3_8 {g(x)} \, dx - \int\limits^3_8 {f(x)} \, dx = -2 - 6 = -8\)
\($3.\;\;\int\limits^3_8 {4f(x)} \, dx - \int\limits^3_8 {2g(x)} \, dx = 24 - 4 = 20\)
To solve more questions on functions & expressions, visit the link below
brainly.com/question/17613163
#SPJ9
Answer:
C. ∫(f·g)dx = -12 is incorrect
Step-by-step explanation:
You want to know which of the integral expressions is incorrect given ...
\(\displaystyle \int_3^8{f(x)}\,dx=6\ \ \text{ and }\int_3^8{g(x)}\,dx=-2\)
LimitsExpression A has the same value for upper and lower limits of the integral. The area being integrated has zero width, so its value will be zero, as shown in expression A.
Expression E has the limits reversed from those in expression B, so the value of that integral will be the opposite of the value shown for B. Both of these integral expressions (B, E) are correct.
SumsThe integral of a sum is the sum of the integrals. This is shown in expressions B, D, and E, all of which are correct.
ProductIn general, the integral of a product will have no relation to the product of integrals. Hence expression C is NOT necessarily correct.
<95141404393>
Calculate the probability current corresponding to the following wave function ψ(r,t)= r
e ikr
Answer: S= mr 2
ℏk
r
^
The teacher started the problem this way: r 2
=x 2
+y 2
+z 2
S= 2m
iℏ[ψ ∗
∇ψ−ψ∇ ∗
]
But I have no idea how to proceed.
Answers
The probability current corresponding to the wave function ψ(r,t) = r e^(ikr) is S = (m r^2 / ℏk) r^.
To calculate the probability current, we start with the expression S = (2m/ℏ) Im[ψ^* ∇ψ - ψ ∇^*]. Given the wave function ψ(r,t) = r e^(ikr), we need to calculate the gradient (∇) and the complex conjugate (∗) of ψ. The gradient of ψ can be computed as ∇ψ = (∂/∂x, ∂/∂y, ∂/∂z) (r e^(ikr)). Applying the derivatives, we obtain ∇ψ = (e^(ikr) + ikr e^(ikr)) (cosθ, sinθ, 0), where θ is the angle between the position vector r and the x-y plane.
The complex conjugate of ψ, ψ^*, is obtained by taking the complex conjugate of each term in ψ. Therefore, ψ^* = r e^(-ikr). Similarly, we calculate ∇^* = (e^(-ikr) - ikr e^(-ikr)) (cosθ, sinθ, 0).
Now we substitute these expressions into the formula for the probability current S. After simplification, we get S = (m r^2 / ℏk) r^, where r^ = (sinθ cosφ, sinθ sinφ, cosθ) is the unit vector in the direction of r.
In summary, the probability current corresponding to the given wave function ψ(r,t) = r e^(ikr) is S = (m r^2 / ℏk) r^. This expression represents the magnitude and direction of the probability current associated with the particle described by the wave function.
Learn more about probability.
brainly.com/question/31828911
#SPJ11
Help me with this Question Please.

Answers
Answer:
\(3 \times \frac{1}{3 } + \frac{1}{2} \times - 12( \frac{1}{3} ) = \frac{1}{3} \)
The half life of a substance is defined as the time required for the substance to decrease by half. If the weight of a substance begins at 128 grams, and the half life is 7 years, what will be the weight of the substance after 28 years?
Answers
the weight of the substance after 28 years is 8 grams.
How to determine the amountWe have that the half life of a substance is defined as the time required for the substance to decrease by half
The formula for calculating the half - life of a material is given as;
\(N(t) = N0 (\frac{1}{2} )^\frac{t}{t^\frac{1}{2} }\)
Where
N(t) is final amountNo is the initial amount = 128 gramst1/2 is the half life = 7 yearst is the time elapsed = 28 yearsSubstitute into the formula
N(t) = 128 × (0. 5) ^28/ 7
N (t) = 128 × ( 0. 5) ^ 4
N(t) = 128 × 0. 0625
N(t) = 8 grams
Thus, the weight of the substance after 28 years is 8 grams.
Learn more about half life here:
https://brainly.com/question/26148784
#SPJ1
find the sum of the series. [infinity] (−1)n2n 32n(2n)! n = 0
Answers
We can use the power series expansion of the exponential function e^(-x) to evaluate the sum of the series:
e^(-x) = ∑(n=0 to infinity) (-1)^n (x^n) / n!
Setting x = 3/2, we get:
e^(-3/2) = ∑(n=0 to infinity) (-1)^n (3/2)^n / n!
Multiplying both sides by (3/2)^2 and simplifying, we get:
(9/4) e^(-3/2) = ∑(n=0 to infinity) (-1)^n (3/2)^(n+2) / (n+2)!
Comparing this with the given series, we can see that they differ only by a factor of (-1) and a shift in the index of summation. Therefore, we can write:
∑(n=0 to infinity) (-1)^n (2n) (3/2)^(2n) / (2n)!
= (-1) ∑(n=0 to infinity) (-1)^n (3/2)^(n+2) / (n+2)!
= (-1) ((9/4) e^(-3/2))
= - (9/4) e^(-3/2)
Hence, the sum of the series is - (9/4) e^(-3/2).
To know more about the series refer here
https://brainly.com/question/24237186
SPJ11
A municipal trash facility allows a person to throw away a maximum of 40 pounds of trash per week. Last week, 195 people threw away the maximum allowable trash. How many tons of trash did this equal
Answers
The total tons of trash that was thrown away by the people is 3.9 tons.
How many tons of thrash was thrown away?The first step is to convert pounds to tons
1 pound = 0.0005 tons
40 x 0.0005 = 0.02 tons
The second step is to multiply 0.02 by 195
0.02 x 195 = 3.9 tons
To learn more about multiplication, please check: https://brainly.com/question/13814687
#SPJ1
convert the polar equation to rectangular form and sketch its graph. r = 2 cot() csc()
Answers
In rectangular form, the given equation is expressed as y = 2x, which represents a straight line passing through the origin with a slope of 2. The graph of this equation in rectangular coordinates is a straight line with a positive slope.
The polar equation r = 2 cot(θ) csc(θ) represents a graph that is symmetric about the x-axis and has vertical asymptotes at θ = 0 and θ = π.
To convert the polar equation r = 2 cot(θ) csc(θ) to rectangular form, we can use the trigonometric identities cot(θ) = cos(θ) / sin(θ) and csc(θ) = 1 / sin(θ).
Substituting these identities into the equation, we have r = 2(cos(θ) / sin(θ))(1 / sin(θ)). Simplifying further, we get r = 2 cos(θ) / sin²(θ).
To convert to rectangular form, we can use the relationship between polar and rectangular coordinates: x = r cos(θ) and y = r sin(θ).
Substituting these equations into the polar equation, we have
y = 2x sin²(θ) / cos(θ).
Simplifying the equation, we get y = 2x tan(θ).
The rectangular equation y = 2x represents a straight line passing through the origin with a slope of 2.
It means that for every unit increase in x, y increases by 2 units. The line is symmetric about the origin and has a positive slope.
As x approaches infinity or negative infinity, y also approaches infinity or negative infinity, respectively.
When sketching the graph, we draw a line passing through the origin with a slope of 2.
The line extends indefinitely in both directions, and all points on the line satisfy the equation y = 2x.
The graph does not intersect the y-axis and has no x-intercept.
Learn more about rectangular coordinates here:
https://brainly.com/question/31904915
#SPJ11
In parallelogram ABCD, the measure of angle A = 3x and the measure of angle B = x + 10.
What is the measure of angle D?

Answers
Answer: 42.5
Step-by-step explanation:
Answer:
52.5, it’s asking for measure d not x, measure d is equal to measure b
Step-by-step explanation:
a=3x, b=x+10,
3x+x+10=180
4x=170
x=42.5
b/d=42.5+10
b/d=52.5
Write a story to represent the equation 15 ÷ 1/9. Solve the equation and complete the story.
Answers
Answer:
Jamie has a foot plank that he needs to cut into 1/9 pieces.
15 ÷ 1/9 = 135
135 x 1/9 = 15
Step-by-step explanation:
land's bend sells a wide variety of outdoor equipment and clothing. the company sells both through mail order and via the internet. random samples of sales receipts were studied for mail-order sales and internet sales, with the total purchase being recorded for each sale. a random sample of 9 sales receipts for mail-order sales results in a mean sale amount of $72.10 with a standard deviation of $27.75 . a random sample of 13 sales receipts for internet sales results in a mean sale amount of $79.00 with a standard deviation of $25.75 . using this data, find the 95% confidence interval for the true mean difference between the mean amount of mail-order purchases and the mean amount of internet purchases. assume that the population variances are not equal and that the two populations are normally distributed. step 1 of 3 : find the critical value that should be used in constructing the confidence interval. round your answer to three decimal places.
Answers
we are 95% confident that the true mean difference between the amount of mail-order purchases and the amount of internet purchases lies between -$23.09 and $9.29.
Step 1: Find the critical value that should be used in constructing the confidence interval.
Since the sample sizes are small (n1=9, n2=13), we will use the t-distribution for the interval estimate. The degrees of freedom is calculated using the formula:
df = [(s1^2/n1 + s2^2/n2)^2] / [((s1^2/n1)^2)/(n1 - 1) + ((s2^2/n2)^2)/(n2 - 1)]
Plugging in the values gives:
df = [(27.75^2/9 + 25.75^2/13)^2] / [((27.75^2/9)^2)/(9 - 1) + ((25.75^2/13)^2)/(13 - 1)] ≈ 17.447
Using a t-table with 17 degrees of freedom and a confidence level of 95%, we find the critical value to be 2.110.
Step 2: Calculate the point estimate of the difference between the means.
The point estimate of the difference between the means is:
1x - x2 = $72.10 - $79.00 = -$6.90
Step 3: Calculate the confidence interval.
The formula for the confidence interval for the difference between two population means is:
(1x - x2) ± tα/2 * sqrt[s1^2/n1 + s2^2/n2]
Plugging in the values gives:
(-$6.90) ± 2.110 * sqrt[27.75^2/9 + 25.75^2/13] ≈ (-$23.09, $9.29)
Therefore, we are 95% confident that the true mean difference between the amount of mail-order purchases and the amount of internet purchases lies between -$23.09 and $9.29.
To learn more about amount click here:brainly.com/question/30690010
#SPJ11
find the number of different ways that 570 contestants can win different first, second and third prizes.
Answers
184,219,440 ways.
What is contestant?
A participant in a contest or competition is known as a contestant. A contestant is someone who challenges election results.
There are 570 contestants, and any one of them can win the first prize.
One of the remaining 569 people can receive the second prize.
Third may be assigned to any of the remaining 568.
We can accomplish this in 570*569*568 ways
= 184,219,440 ways.
To learn more about contestant checkout https://brainly.com/question/27896050
#SPJ4
two trains going in opposite directions leave at the same time. one train tave4ls 15 mph faster than the other. in 6 hours the trains are 630 miles apart. find the speed of each
Answers
Using the formula of speed, the speed of first trains is 45 mph and the speed of second train is 60 mph.
In the given question, we have to find the speed of each.
Two trains going in opposite directions leave at the same time.
One train tavels 15 mph faster than the other.
In 6 hours the trains are 630 miles apart.
Let the speed of the first vehicle be s mph, then according to the question, the speed of the second vehicle would be (s+15) mph.
Let the first vehicle covers the distance D(1) and the second one D(2) in the prescribed time.
So, find the distance covered by the first vehicle in 6 hours by using the formula
Distance = Speed × Time
So the distance D(1) is;
D(1) = s*6
D(1) = 6s
So the distance D(2) is;
D(2) = (s+15)*6
D(2) = 6s+90
Since, after 6 hours both the vehicles are at the distance 630 miles. So, the sum of the two distances D(1) and D(2) will be equal to 630.
D(1)+D(2) = 630
Puttimg the value of D(1) and D(2)
6s+6s+90=630
Simplifying
12s+90=630
Subtract 90 on both side we get
12s=540
Divide by 12 on both side we get
s=45 mph
So the value of speed of the faster vehicle
s+15 = 45+15
s+15 = 60 mph
Hence, the speed of first train is 45 mph and the speed of second train is 60 mph.
To learn more about the formula of speed link is here
brainly.com/question/3004254
#SPJ4
I WILL GIVE BRAINLIEST!!!!!!!!!!!!!)there are 56 tulips in a flowerbed. the ratio of tulips to daffodils is 3:5. how many tulips and how many daffodils are there in a flowerbed? (Pls answer correctly)
Answers
Answer:
tulips= 56
and daffodils= 93
Step-by-step explanation:
Step one:
given data
number of tulips = 56
ratio of tulips to daffodiis= 3:5
total ratio= 3+5= 8
Step two:
Required
The number pf daffodiis
let us apply the part to all aproach
the total flowers can be found bellow
let the total be x
3/8=56/x
cross multiply
3x=56*8
3x=448
divide both sides by 3
x=448/3
x=149.3
=149 approx.
The total flowers is 149
the number of daffodils is =149-56=93
tulips= 56
and daffodils= 93
Answer:
21 tuilps : 35 daffodils
Step-by-step explanation
There are 3 : 5 = 3+5=8
3= tulips
5=daffodils
8 parts of the bed
=
3/8*56 = 21 (tuilips)
5/8*56 = 35(daffodils)
Thus we have 21 tuilips and 35 daffadils (21:35)
determine the value of x.

Answers
Answer: 1) -5.8
Step-by-step explanation:
in order to solve the problem you have to put it together:
9x-5 = 14x+24
then go from there : subtract 24 on both sides , then subtract 9x on both sides , that’ll leave you with : -29 = 5x
so from there we divide , giving us x= -5.8
Roscoe is a professional groomer.
What is the unit rate for grooming per hour?
5 dogs per hour
15 dogs per hour
3 dogs per hour
1 dog per hour
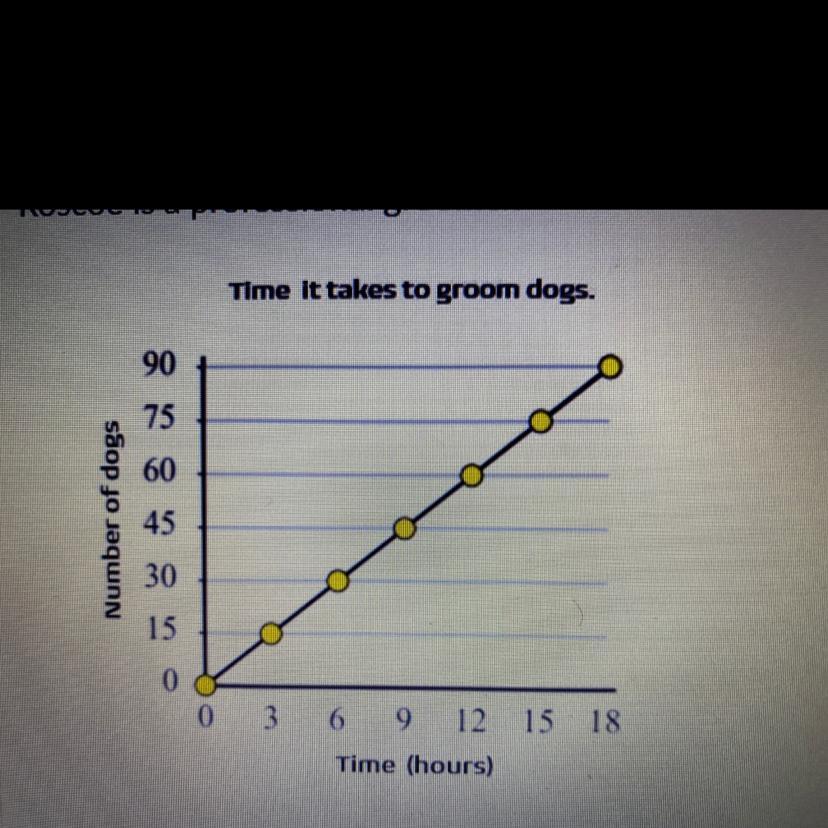
Answers
You need to divide the 15 dogs by the 3 hours to get your one hour.
The population of china was about 1. 39 billion in the year 2013, with an annual growth rate of about 0. 6%. Find an equation p(t) that represents the growth function for china. Write your answer in the form a(b)t, in billions.
Answers
The equation that represents china growth function is
P(t) = 1.39 * ( 1.006)ⁿ.
What is a function?
function is a mathematical phrase, rule, or law that establishes the relationship between an independent variable and a dependent variable (the dependent variable).
The initial population = 1.39 billion in 2013
Growth rate = 0.6%
Let a be the initial population
Let b be the growth rate
Let n be the elapsed year from 2013
Let the population in nay year be P(t)
Then equation is
P(t) = a * ( b )ⁿ
P(t) = 1.39 * ( 1.006)ⁿ
∴ The equation P(t) represents the growth function of china
To learn more about a function from the given link
https://brainly.com/question/22872880
#SPJ4
help asap! Write the equation of the circle graphed below.

Answers
The equation for the circle in the graph is:
(x + 2)² + (y + 2)² = 0.5625
How to write the circle equation?A circle whose center is at the point (a, b) and has a radius of R units can be written as:
(x - a)² + (y - b)² = R²
Here we can see in the graph that the center of the circle is at the point (-2, -2), and we also can see that the radius of the circle is 0.75 units, then the equation for the circle in the graph will be:
(x - (-2))² + (y - (-2))² = 0.75²
We can simplify that to get:
(x + 2)² + (y + 2)² = 0.5625
That is the equation.
Learn more about circles at:
https://brainly.com/question/1559324
#SPJ1
What is the circumference of this circle? Use 3.14 for π

Answers
Answer:
37.68
Step-by-step explanation:
C= Pie x C
C = 3.14 x 12
37.68 cm
Step-by-step explanation:
Circumference =?
π = 3.14
d = 12
Circumference = πd
Substitute values into the given equation
\(c = 3.14 \times 12 \\ c = 37.68 \: cm\)
Identify the missing factors:
d) 20 = (4) (?)
e) -14x = (7)(?)
f) x3 =x2 (?)
Answers
Ur solution is in the attachment.

Answer:
d) ? = 5
e) ? = -2x
f) ? = x
Step-by-step explanation:
d) 20 = (4)(?)
20/4 = ?
5 = ?
Check:
20 = 4*5
e) -14x = (7)(?)
-14x/7 = ?
-2x = ?
Check:
-14x = 7*-2x
f) x³ =x² (?)
x³/x² = ?
x³⁻² = ?
x¹ = ?
x = ?
Check:
x³ = (x²)(x)
Which the is the correct answer?

Answers
To solve this problem, we need to use combination which is statistical tool to determine the number of ways an event may occur. The combination to select a 5 a side team from 12 students is 792.
CombinationThis a mathematical technique that is used to determine the number of possible arrangements in a collection of items where the way they're arranged does not matter.
Data;
Number of Students = 12Team = 5The combination for this would be
\(C = ^1^2C_5 = 792\)
The combination to select a 5 a side team from 12 students is 792.
Learn more on combination here;
https://brainly.com/question/251701
#SPJ1
Graph the following:
(x - 1)2 + (y - 3)2 = 4
Center
Radius
Answers
Answer:
Center = (1,2) radius = 2
Step-by-step explanation:
I used Demos to graph the circle.
Then I added two line to find the center of the circle
The radius is 2
Asp help will give brainliest

Answers
Answer:
answer is 30 pls mark me branilest