12(x - 1) = - 4(3-X) + 8x
Answers
This equation has infinite solutions, any real number makes it true.
Related Questions
Please help me with this
Answers
The volume of rectangular prism is 90 unit³.
We can consider the 1 block = 1 unit.
Length of prism = 5 unit
width of prism = 6 unit
Height of prism = 3 unit
So, Volume of rectangular prism
= l w h
= 5 x 6 x 3
= 90 unit³
Thus, the volume of rectangular prism is 90 unit³.
Learn more about Volume here:
https://brainly.com/question/1578538
#SPJ1
Use the compound interest formula to compute the balance in the following account after the stated period of time, assuming interest is compounded annually.
$7000 invested at an APR of 3.3% for 13 years
The balance in the account after 13 years is $___
Answers
The balance in the account after 13 years is $8233.79.
Compound interest: Calculating balance in an accountFrom the question, we are to use the compound interest formula to compute the balance in the account
From the compound interest formula, we have that
A = P(1 + r/n)^nt
Where A is the amount
P is the principal
r is the interest rate
n is the number of times compounded per year
and t is the time.
From the given information,
P = $7000
r = 3.3%= 0.033
n = 1
t = 13
Putting the parameters into the formula
A = P(1 + r/n)^nt
A = 7000(1 + 0.033/1)^(1×5)
A = 7000(1 + 0.033)^5
A = $8233.79
Hence, the balance is $8233.79
Learn more on Compound interest here: https://brainly.com/question/25545513
#SPJ1
Ali, Basti and Cian stand at three points A, B and C respectively. Suppose that the measure of angle ABC is 50 degrees , the measure of angle BAC is 60 degrees and Ali is exactly 150 ft away from Basti. Find the distance between Basti and Cian.
Answers
The distance between Basti and Cian is approximately 138.2 ft. Option D
To find the distance between Basti and Cian, we can use the Law of Sines, which relates the lengths of sides to the sines of their opposite angles in a triangle.
Let's label the points: A, B, and C. Ali is at point A, Basti is at point B, and Cian is at point C.
Given:
Angle ABC = 50 degrees (angle opposite side AC)
Angle BAC = 60 degrees (angle opposite side BC)
Ali is 150 ft away from Basti (side AB)
We want to find the distance between Basti and Cian, which is side BC.
Using the Law of Sines, we have:
BC/sin(50) = AB/sin(60)
Substituting the known values:
BC/sin(50) = 150/sin(60)
To find BC, we can rearrange the equation:
BC = (150/sin(60)) * sin(50)
Using a calculator to evaluate the expression:
BC ≈ 138.2 ft
Option D is correct.
For more such questions on distance visit:
https://brainly.com/question/30395212
#SPJ8
Name the marked angle in 2 different ways.MKSubmit Answerattempt 1 out of 2
Answers
In the given triangle, we are asked to name the marked angles in two different ways.
The point L indicates the location of the vertex. This is the point where two rays meet to form an angle.
We can name the marked angle using two methods:
1) By three capital letters with the vertex in the middle.
2)By one capital letter using the letter that indicates the vertex.
Therefore, the possible names of the marked angles would be:
Answer:
leon wrote an expression that is equivalent to (30 + 6) ÷ 12 which expression could be the one Leon wrote A. 36÷3 • 4 B.(3 • 3 • 4) ÷ 4 • 3 C. 5 • 6+2 • 3 ÷ 3 • 2 • 2D. (3 • 3 • 2 • 2) ÷ (3 • 2 • 2) and explain why you chose A, B, C, or D
Answers
First lets simplify;
(30 + 6) ÷ 12
Using PEMDAS
36 ÷ 12 = 3
Lets check option A
Using PEMDAS
36÷3 • 4 = 12 • 4 = 48
This means A is not the correct option
We move to B.
(3 • 3 • 4) ÷ 4 • 3
Using PEMDAS
we solve the bracket
36 ÷ 4 • 3 = 9 • 3 =27
B is not the option.
We move to C
5 • 6+2 • 3 ÷ 3 • 2 • 2
Using PEMDAS
30 + 6÷ 3 • 2 • 2
= 30 + 2 • 2 • 2
=30 +8
=38
C is not the option
We move to option D
(3 • 3 • 2 • 2) ÷ (3 • 2 • 2)
Using PEMDAS, we will solve the parenthesis first
36 ÷ 12 = 3
Therefore option D is the correct options.
Option D is equivalent to (30 + 6) ÷ 12
Find g(x), where g(x) is the reflection across the y-axis of f(x)= –9|x–10|+1.
Answers
Answer:
To reflect a graph, f(x) over the x-axis, you take -f(x).
So if f(x)=x^2, then -f(x) is -x^2.
Then g(x)=-x^2 is the reflection of your function f(x) over the x-axis.
Step-by-step explanation:
What is the volume of this cone? Use 3.14 for π and round your answer to the nearest tenth.
In your answer, give the volume of the cone rounded to the nearest tenth, and then explain how you calculated it.
Answers
Answer:
volume = 33.5 in³
Step-by-step explanation:
Formula:
\(\sf volume \ of \ a \ cone=\dfrac13\pi r^2h\)
Given:
r = 2 inh = 8 inπ = 3.14Substituting the given values into the formula:
\(\sf \implies volume=\dfrac13 \times 3.14 \times 2^2 \times 8\)
\(=\dfrac13 \times 3.14 \times 4 \times 8\)
\(\sf =33.49333333...\)
\(\sf =33.5 \ in^3 \ (nearest \ tenth)\)
Use the interval notation to represent all values of ex satisfying the given conditions.
Answers
Notice that solving the given problem is equivalent to solving
\(|3x-8|+2<8,\)for x.
Adding -2 to both sides of inequality we get:
\(|3x-8|<8-2=6.\)Now, recall that:
\(|a|Therefore, we can rewrite the last inequality as:\(-6<3x-8<6.\)Adding 8 we get:
\(\begin{gathered} -6+8<3x-8+8<6+8, \\ 2<3x<14. \end{gathered}\)Finally, dividing by 3, we get:
\(\frac{2}{3}The above result in interval notation is:\((\frac{2}{3},\frac{14}{3})\text{.}\)Answer:
\((\frac{2}{3},\frac{14}{3})\text{.}\)Find the dimensions of a rectangle (in m) with area 1,000 m2 whose perimeter is as small as possible. (Enter the dimensions as a comma separated list.)
Answers
The perimeter of the rectangle is the sum of its dimensions
The dimensions that minimize the perimeter are \(\mathbf{10\sqrt{10 },10\sqrt{10 }}\)
The area is given as:
\(\mathbf{A = 1000}\)
Let the dimension be x and y.
So, we have:
\(\mathbf{A = xy = 1000}\)
Make x the subject
\(\mathbf{x = \frac{1000}{y}}\)
The perimeter is calculated as:
\(\mathbf{P = 2(x + y)}\)
Substitute \(\mathbf{x = \frac{1000}{y}}\)
\(\mathbf{P = 2(\frac{1000}{y} + y)}\)
Expand
\(\mathbf{P = \frac{2000}{y} + 2y}\)
Differentiate
\(\mathbf{P' = -\frac{2000}{y^2} + 2}\)
Set to 0
\(\mathbf{ -\frac{2000}{y^2} + 2 = 0}\)
Rewrite as:
\(\mathbf{ -\frac{2000}{y^2} = -2}\)
Divide both sides by -1
\(\mathbf{\frac{2000}{y^2} = 2}\)
Multiply y^2
\(\mathbf{2000 = 2y^2}\)
Divide by 2
\(\mathbf{1000 = y^2}\)
Take square roots of both sides
\(\mathbf{y = \sqrt{1000 }}\)
\(\mathbf{y = 10\sqrt{10 }}\)
Substitute \(\mathbf{y = \sqrt{1000 }}\) in \(\mathbf{x = \frac{1000}{y}}\)
\(\mathbf{x = \frac{1000}{\sqrt{1000}}}\)
\(\mathbf{x = \sqrt{1000}}\)
\(\mathbf{x = 10\sqrt{10 }}\)
Hence, the dimensions that minimize the perimeter are \(\mathbf{10\sqrt{10 },10\sqrt{10 }}\)
Read more about perimeters at:
https://brainly.com/question/6465134
Pls send only answers - no work
Answers
Answer:
No
Step-by-step explanation:
If you are just seeking answers, you are basically cheating and trying to get someone to do your work...which will not help you learn the material ....sad.
A manufacturing company plans to progressively increase its production capacity over the next few quarters. (A quarter is a period of three months.) The increase in production can be modeled by the equation y = x6 − 25x4 + 199x2, where x is the number of quarters. What is the minimum duration required for the company to reach a production capacity of 4,975 units?
Answers
Answer:
5 months
Step-by-step explanation:
We assume that y represents production capacity, rather than increase in production capacity. Then we want to solve the 6th-degree equation ...
x^6 -25x^4 +199x^2 -4975 = 0
This can be factored in groups as ...
x^4(x^2 -25) + 199(x^2 -25) = 0
(x^4 +199)(x^2 -25) = 0
This has 4 complex solutions and 2 real solutions.
x^2 = 25
x = ±5
The duration required for capacity to reach 4975 units is 5 months.
The area of a square is 100 square centimeters. what is the perimeter
Answers
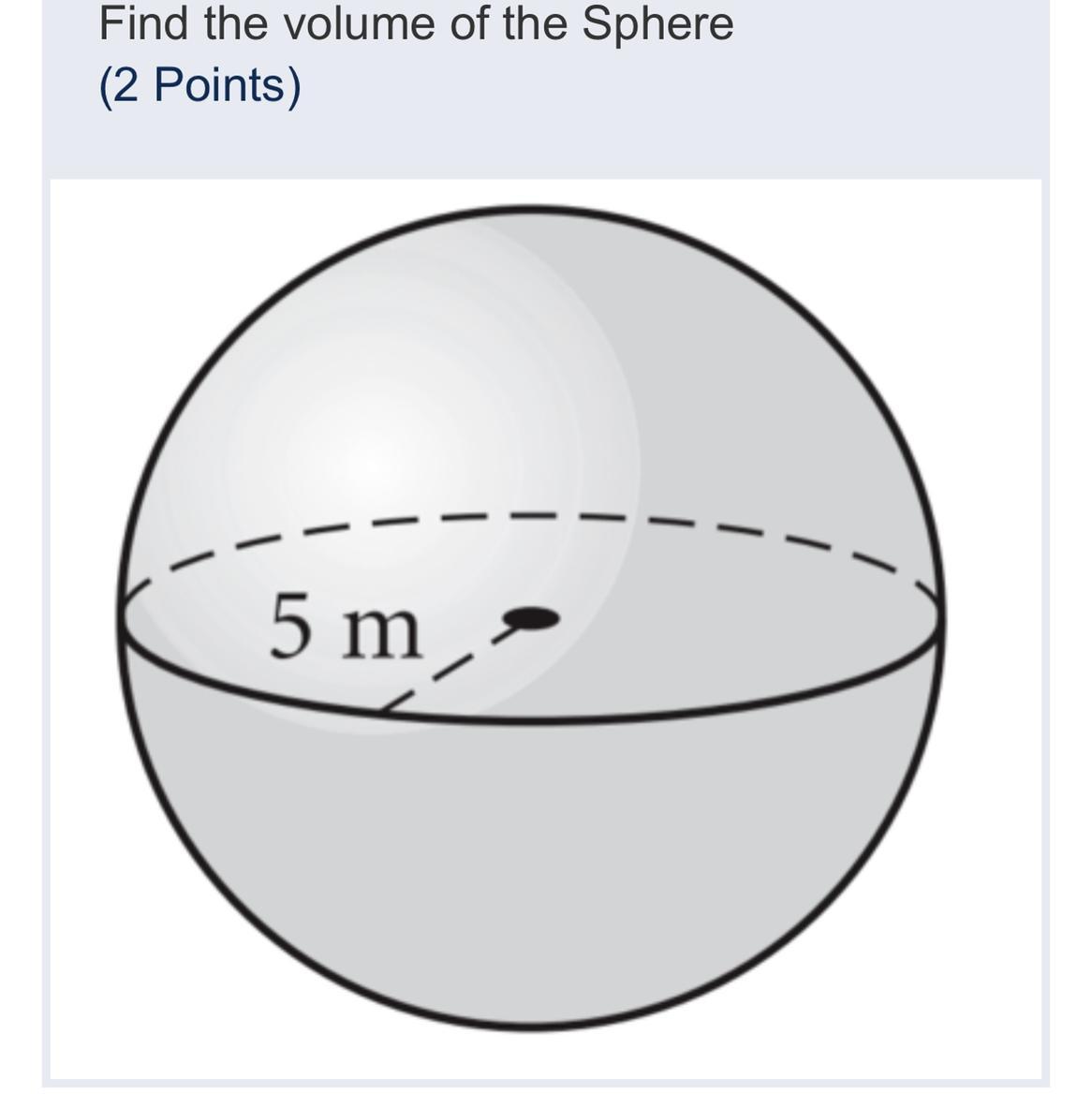
Answer:
Step-by-step explanation:
area of a square = S x S
side = ⱱarea
side = ⱱ100
side = 10cm
perimeter = 4s
= 4 x 10
=40cm
a rectangle with a width of 30 centimeters has a perimiter of 100 centimeters to 160 centimeters graph a compound inequality
Answers
Answer:
5 ≤ L ≤ 35
Step-by-step explanation:
Let w represent the width of the rectangle.
The perimeter (P) of the rectangle is given by:
P = 2w + 2L
Where L is the length of the rectangle.
We know that w = 30 cm and that the perimeter is between 100 and 160 cm. We can now set up our compound inequality:
100 ≤ 2(30) + 2L ≤ 160
100 ≤ 90 + 2L ≤ 160
10 ≤ 2L ≤ 70
We can now divide both sides by 2 to solve for L:
5 ≤ L ≤ 35
Therefore, the compound inequality that represents the graph of a rectangle with a width of 30 centimeters and a perimeter of 100 centimeters to 160 centimeters is: 5 ≤ L ≤ 35
What is one result of meiosis?
A) a larger organism
B) Identical daughter cells
C) repair of damaged cells
D) Formation of gametes
Answers
Answer:
The formation of gametes is one result of meiosis.
Which of the following coordinate points have a y-value of 6? Select all that apply.
A) (3, 6)
B) (6, 5)
C) (8, 6)
D) (1, 6)
Answers
Answer
A, C, and D
Step-by-step explanation:
You are trying to find the y value in (x,y) form. Therefore, it has to be A, C, and D because they all have a 6 in the y value.
SCALCET8 3.9.015. A street light is mounted at the top of a 15-ft-tall pole. A man 6 ft tall walks away from the pole with a speed of 4 ft/s along a straight path. How fast is the tip of his shadow moving when he is 35 ft from the pole
Answers
Answer:
\(X=6.67ft/s\)
Step-by-step explanation:
From the question we are told that:
Height of pole \(H_p=15\)
Height of man \(h_m=6ft\)
Speed of Man \(\triangle a =4ft/s\)
Distance from pole \(d=35ft\)
Let
Distance from pole to man=a
Distance from man to shadow =b
Therefore
\(\frac{a+b}{15}=\frac{b}{6}\)
\(6a+6b=15y\)
\(2a=3b\)
Generally the equation for change in velocity is mathematically given by
\(2(\triangle a)=3(\triangle b )\)
\(2*4=3(\triangle b)\)
\(\triangle a=\frac{8}{3}\)
Since
The speed of the shadow is given as
\(X=\triangle b+\triangle a\)
\(X=4+8/3\)
\(X=6.67ft/s\)
What is the value of 45 root 3?
Answers
Rounding to five decimal places, the cube root of 45 equals 3.55689. This is the accurate answer to the equation x3 = 45.
In Mathematics, what do you mean by Root ?In mathematics, a root is the answer to an equation, which is typically given as a number or an algebraic formula.
Quadratic equation's roots The roots of a quadratic equation are the values of the variables that fulfill the equation. In other words, if f() = 0, then x = is a root of the quadratic equation f(x). The x-coordinates of the sites where the curve y = f(x) intersects the x-axis are the real roots of an equation f(x) = 0.In mathematics, a root is the answer to an equation, which is typically given as a number or an algebraic formula.One of a number's equal elements was commonly referred to as the "root" by Arab writers in the ninth century, and the Latin word "radix" was employed by its medieval European translators (from which derives the adjective radical).Therefore, the expression for the square root of 45 is 45 = (9 5) = 3/5. Since 45 is not a square that is perfectly square, it falls within roots. The square root of 45 is represented by the simplified radical 35.To know more about Root please click here ; https://brainly.com/question/428672
#SPJ4
x power 8 + x power 4 + 1
factorize
Answers
Answer:
\(1(x {}^{8} + x {}^{4} + 1)\)
Step-by-step explanation:
\(x {}^{8} + {x}^{4} + 1 =1( x {}^{8} + x {}^{2} + 1)\)
Hope this helps ;) ❤❤❤
Let me know if there is an error in my answer.
Explanation:
x^8 + x^4 + 1 = 0
(x^8 + x^4) + 1 = 0
x^4(x^4 + 1) + 1 = 0
(x^4 + 1)(x^4 + 1) = 0
70 POINTS PLEASE HELP ASAP
The linear functions f(x) and g(x) are represented on the graph, where g(x) is a transformation of f(x):
A graph with two linear functions; f of x passes through 1, 3 and 3, 13, and g of x passes through negative 1, 3 and 1, 13.
Part A: Describe two types of transformations that can be used to transform f(x) to g(x). (2 points)
Part B: Solve for k in each type of transformation. (4 points)
Part C: Write an equation for each type of transformation that can be used to transform f(x) to g(x). (4 points)
Answers
Answer:
Part A: The two types of types of transformation are
1) Rotation of 11.3° about (1, 2)
2) By algebraic transformation
Part B:
Rotation by 11.3° and T(2 - y)×1/2 + x, 0)
Part C: The transformation that can be used to transform f(x) to g(x) is T(2 - y)×1/2 + x, 0)
Step-by-step explanation:
The coordinates through which the linear function f(x) passes = (1. 3) and (3, 13)
The coordinates through which the linear function g(x) passes = (1, 3) and (1, 13)
The equation for f(x) in slope and intercept form. y = m·x + c is given as follows;
The slope, m = (13 - 3)/(3 - 1) = 5
The equation in point and slope form is y - 3 = 5×(x -1)
y = 5·x - 5 + 3 = 5·x - 3
y = 5·x - 3
The equation for g(x) in slope and intercept form. y = m·x + c is given as follows;
The slope, m = (13 - 3)/(1 - 1) = ∞
∴ The equation in point and slope form is x = 1
Therefore, the two equations meet at the point (1, 2)
The transformation that can be used to transform f(x) to g(x) is T(2 - y)×1/2 + x, 0)
2) Another transformation that can be used is to rotate f(x) by the vertex angle as follows
Vertex angle is 90° - tan⁻¹(m) = 90° - tan⁻¹(5) ≈ 11.3°
Rotation of f(x) by 11.3° about (1, 2) gives g(x)
Step-by-step explanation:
What is the minimum product of two numbers whose difference is 36? What are the numbers?
Answers
36 - 0 = 36
36 x 0 = 0
Seems like that’s the answer
Which of the following is a radical equation?
a. x StartRoot 3 EndRoot = 13
b. x + StartRoot 3 EndRoot = 13
c. StartRoot x EndRoot + 3 = 13
d. x + 3 = StartRoot 13 EndRoot
Answers
Answer:
the answer is D
Step-by-step explanation:
What is an equation of the line that passes through the points (5, 5) and (-5, -7)?
Answers
Answer:
y= 6/5x - 1
Step-by-step explanation:
Hi there!
We are given the points (5, 5) and (-5, -7). We want to find the equation of the line that passes through those points
There are 3 ways to write the equation of the line, but the most common way is slope-intercept form, which is y=mx+b, where m is the slope and b is the y intercept
So, first we need to find the slope
The slope can be calculated from 2 points using the formula \(\frac{y_2-y_1}{x_2-x_1}\), where \((x_1, y_1)\) and \((x_2, y_2)\) are points
We have 2 points, but let's label their values to avoid any confusion when calculating.
\(x_1=5\\y_1=5\\x_2=-5\\y_2=-7\)
Now substitute these values into the formula.
m=\(\frac{y_2-y_1}{x_2-x_1}\)
m=\(\frac{-7-5}{-5-5}\)
Subtract
m=\(\frac{-12}{-10}\)
Simplify
m=\(\frac{6}{5}\)
The slope of the line is 6/5
We can substitute that as m in y=mx+b
Here is the equation of the line so far:
y=6/5x+b
Now we need to find b
As the equation passes through the points (5, 5) and (-5, -7), we can use either one of them to help solve for b
Using (5,5) for example:
5=6/5(5)+b
Multiply
5=6+b
Subtract 6 from both sides
-1=b
Substitute -1 as b:
y= 6/5x - 1
Hope this helps!
See more on this topic here: https://brainly.com/question/27185456
Sam has a deck that is shaped like a triangle with a base of 18 feet and a height of 7 feet. He plans to build a 2:5 scaled version of the deck next to his horse's water trough.
Part A: What are the dimensions of the new deck, in feet? Show every step of your work. (4 points)
Part B: What is the area of the original deck and the new deck, in square feet? Show every step of your work. (4 points)
Part C: Compare the ratio of the areas to the scale factor. Show every step of your work. (4 points)
Answers
The 2 : 5 scaled version of the deck Sam plans to build and the dimensions of the original deck indicates;
Part A; Base length of the new deck = 7.2 feet
Height of the new deck = 2.8 feet
Part B; The area of the original deck is 63 square feet
The area of the new deck is 10.08 square feet
Part C; The ratio of the areas is the square of the scale factor
What is a scale factor?A scale factor is a number or factor that is used to enlarge or reduce the dimensions a shape or size of a figure.
The base length of the triangular deck = 18 feet
The height of the triangular deck = 7 feet
The scale factor for the scaled version Sam intends to build = 2 : 5
Part A; The dimensions of the new deck are;
Base length of the new deck using the the 2 : 5 ratio is; (2/5) × 18 = 7.2 feet
The height of the new deck = (2/5) × 7 = 2.8 feet
Part B; The area of the original deck = (1/2) × 18 × 7 = 63 square feet
Area of the new dec = (1/2) × 7.2 × 2.8 = 10.08 square feet
Part C; The ratio of the areas is; 10.08/63
Ratio of the area = 10.08/63 = 4/25 = 4 : 25
The scale factor is; 2 : 5
Therefore, the ratio of the area is the square of the scale factorLearn more on scale factors here: https://brainly.com/question/28822248
#SPJ1
The sector of a circle has an area of 104pi/9
square inches and a central angle with measure 65 degree
. What is the radius of the circle, in inches?
Answers
Answer:
Given:
Area of the sector (A) = 104π/9 square inches
Central angle (θ) = 65 degrees
The formula for the area of a sector of a circle is:
A = (θ/360) * π * r^2
We can rearrange this formula to solve for the radius (r):
r^2 = (A * 360) / (θ * π)
Plugging in the given values:
r^2 = (104π/9 * 360) / (65 * π)
r^2 = (104 * 40) / 9
r^2 = 4160 / 9
r^2 ≈ 462.22
Taking the square root of both sides:
r ≈ √462.22
r ≈ 21.49
Therefore, the radius of the circle is approximately 21.49 inches.
Answer: 8 inches
Step-by-step explanation:
what is 2 +2 { 25 points }
1. 22
2. 4
Answers
Answer:
4
Step-by-step explanation:
if you have 2 apples and you get 2 more apples how many do you have.
Find the product
3(z+4)(x-5)
Answers
Answer:
3zx-15z+12x-60
Step-by-step explanation:
first do parenthesis and distribute (z+4)(x-5) into zx-5z+4x-20
then distribute the 3 to get the answer
Find the volume of the sphere of 5m
Answers
Step-by-Step Solution:
Radius (r) = 5 m
Volume of a Sphere (V) = 4/3 πr^3
Therefore,
= 4/3 πr^3
= 4/3 * 22/7 * (5)^3
= 4/3 * 22/7 * 125
= 88/21 * 125
= 11000/21
=> 523.8
Volume of the Sphere (V) = 523.8 m^3
Solve the system of equations by substitution.
3x - 4y = 13
5x + 4y = 11
The solution of the system is x = and y=
(Type integers or simplified fractions.)
Answers
Answer:
\(\mathrm{The\:solutions\:to\:the\:system\:of\:equations\:are:}\)
\(x=3,\:y=-1\)
Step-by-step explanation:
\(3x - 4y = 13\)
\(5x + 4y = 11\)
isolate x for 3x-4y=13
\(\mathrm{Subsititute\:}x=\frac{13+4y}{3}\)
\(\begin{bmatrix}5\cdot \frac{13+4y}{3}+4y=11\end{bmatrix}\)
\(\frac{65+32y}{3}=11\)
now isolate y for \(\frac{65+32y}{3}=11\)
\(\frac{65+32y}{3}=11\)
\(65+32y=33\)
\(32y=-32\)
Divide both sides by 32
\(\frac{32y}{32}=\frac{-32}{32}\)
\(y=-1\)
\(\mathrm{For\:}x=\frac{13+4y}{3}\)
\(\mathrm{Subsititute\:}y=-1\)
\(x=\frac{13+4\left(-1\right)}{3}\)
\(=\frac{13-4\cdot \:1}{3}\)
\(=\frac{9}{3}\)
\(\mathrm{Divide\:the\:numbers:}\:\frac{9}{3}=3\)
\(=3\)
\(\mathrm{The\:solutions\:to\:the\:system\:of\:equations\:are:}\)
\(x=3,\:y=-1\)
3 to the power of 5 = 243. Explain how to use that fact to quickly evaluate 3 to the power of 6
Answers
Step-by-step explanation:
3^6 = 3 * 3^5
= 3 * 243 = 729
6) Which statement about the ladder is true?
A. The ladder has parallel line
segments only.
B. The ladder has perpendicular line segments only.
C. The ladder has parallel line
segments and perpendicular line
segments.
D. The ladder has neither parallel line segments nor perpendicular line segments.
Answers
The true statement about a ladder is; the ladder has parallel line segments and perpendicular line segments.
Parallel lineParallel lines are lines that never meet on the same plane which have equal distance apart from each other.
Perpendicular lineThey are lines that intersect each other to form a right angle.
Therefore, the ladder has parallel line segments and perpendicular line segments.
Learn more about parallel line:
https://brainly.com/question/26961508
#SPJ1