1/3 + 2/5

A. 3/8
B. 11/15
C. 3/3
D. 3/5​

The correct statements regarding the data-set are given as follows:

The consistency of the data-set is obtained by the IQR of each data-set, subtracting Q3 by Q1, hence:

Due to the lower IQR, the clerks from store A were more consistent.

For mean/median, the lower the mean and median, the faster they were.

More can be learned about mean and median at https://brainly.com/question/14532771

#SPJ1

Answer: \(r=\dfrac{4}{\theta}\text{ cm}\) .

Step-by-step explanation:

We know that , \(l= r\theta\) , where l = length of arc , r= radius , \(\theta=\) central angle ( in radians).

Here , l= 4 cm

Substitute this value in the formula , we get

\(4=r\theta \\\\\Rightarrow\ r=\dfrac{4}{\theta}\)

Hence, the formula of r in terms of \(\theta\) is \(r=\dfrac{4}{\theta}\text{ cm}\) , where \(\theta=\) central angle ( in radians).

Answer: 4/θ

Step-by-step explanation: Khan Academy

Answer:

62.5

Step-by-step explanation:

Percentage Calculator: 15 is what percent of 24? = 62.5.

The exact value of sin(u-v) is -77/85. This can be answered by the concept of Trigonometry.

Given the information, we can find the exact value of sin(u-v).

We know that sin(u) = -3/5 and cos(v) = 15/17. Since 3/2 < u < 2, u is in the fourth quadrant where sin is negative, and 0 < v < π/2, v is in the first quadrant where cos is positive.

We can use the trigonometric identity for sin(u-v): sin(u-v) = sin(u)cos(v) - cos(u)sin(v).

First, we need to find cos(u) and sin(v). We can use the Pythagorean identities: sin²(u) + cos²(u) = 1 and sin²(v) + cos²(v) = 1.

For u:
sin²(u) = (-3/5)² = 9/25
cos²(u) = 1 - sin²(u) = 1 - 9/25 = 16/25
cos(u) = √(16/25) = 4/5 (cos is positive in the fourth quadrant)

For v:
cos²(v) = (15/17)² = 225/289
sin²(v) = 1 - cos²(v) = 1 - 225/289 = 64/289
sin(v) = √(64/289) = 8/17 (sin is positive in the first quadrant)

Now we can use the identity sin(u-v) = sin(u)cos(v) - cos(u)sin(v):
sin(u-v) = (-3/5)(15/17) - (4/5)(8/17) = -45/85 - 32/85 = -77/85

So, the exact value of sin(u-v) is -77/85.

To learn more about Trigonometry here:

brainly.com/question/29002217#

#SPJ11

Given vector field, F(x, y, z) = y cos (xy) i + x cos (xy) j – sin z k To calculate the curl of F, we need to take the curl of each component and subtract as follows,∇ × F = ( ∂Q/∂y - ∂P/∂z ) i + ( ∂P/∂z - ∂R/∂x ) j + ( ∂R/∂x - ∂Q/∂y ) k...where P = y cos(xy), Q = x cos(xy), R = -sin(z)

Now we calculate the partial derivatives as follows,

∂P/∂z = 0, ∂Q/∂y = cos(xy) - xy sin(xy), ∂R/∂x = 0...

and,

∂P/∂y = cos(xy) - xy sin(xy), ∂Q/∂z = 0, ∂R/∂y = 0

Therefore,

∇ × F = (cos(xy) - xy sin(xy)) i - sin(z)j

The curl of F is given by:

(cos(xy) - xy sin(xy)) i - sin(z)j.

To state whether F is conservative, we need to determine if it is a conservative field or not. This means that the curl of F should be zero for it to be conservative. The curl of F is not equal to zero. Hence, the vector field F is not conservative. Let C be the curve joining the origin (0,1,-1) to the point with coordinates (1, 2V2,2) defined by the following parametric curve:

r(t) = n* i + t}j + tcos atk, 15t52.

The curve C is defined as follows,r(t) = ni + tj + tk cos(at), 0 ≤ t ≤ 1Given vector field, F(x, y, z) = y cos(xy) i + x cos(xy)j – sin zk Using the curve parameterization, we get the line integral as follows,∫CF.dr = ∫10 F(r(t)).r'(t)dt...where r'(t) is the derivative of r(t) with respect to t

= ∫10 [(t cos(at))(cos(n t)) i + (n cos(nt))(cos(nt)) j + (-sin(tk cos(at)))(a sin(at)) k] . [i + j + a tk sin(at)] dt

= ∫10 [(t cos(at))(cos(n t)) + (n cos(nt))(cos(nt)) + (-a t sin(at) cos(tk))(a sin(at))] dt

= ∫10 [(t cos(at))(cos(n t)) + (n cos(nt))(cos(nt)) - a^2 (t/2) (sin(2at))] dt

= [sin(at) sin(nt) - (a/2) t^2 cos(2at)]0^1

= sin(a) sin(n) - (a/2) cos(2a)

The vector field F(x, y, z) = y cos(xy) i + x cos(xy)j – sin zk is given. Firstly, we need to calculate the curl of F. This involves taking the curl of each component of F and subtracting. After calculating the partial derivatives of each component, we get the curl of F as (cos(xy) - xy sin(xy)) i - sin(z)j. Next, we need to determine whether F is conservative. A conservative field has a curl equal to zero. As the curl of F is not equal to zero, it is not a conservative field. In the second part of the problem, we have to calculate the scalar line integral of the vector field F. dr along the curve C joining the origin to the point with coordinates (1, 2V2, 2). We use the curve parameterization to calculate the line integral. After simplifying the expression, we get the answer as sin(a) sin(n) - (a/2) cos(2a).

The curl of the given vector field F(x, y, z) = y cos(xy) i + x cos(xy)j – sin zk is (cos(xy) - xy sin(xy)) i - sin(z)j. F is not conservative as its curl is not zero. The scalar line integral of the vector field F along the curve C joining the origin to the point with coordinates (1, 2V2,2) is sin(a) sin(n) - (a/2) cos(2a).

To learn more about curve parameterization visit:

brainly.com/question/12982907

#SPJ11

Answer: A random variable.

Step-by-step explanation:

a numerical description of the outcome of an experiment is called a random variable.

The side of the square of each block = 2 feet

Given,

Shelly sews a square blanket that has an area of 144 square feet.

and,  it has 36 square blocks, each the same size.

To find the approximate length of each side of a block

Now, According to the question:

36 square blocks of same size. We need to find the area of each square block. so we divide = area / square blocks

= 144/ 36

= 4

The area of each square = 4 square feet

We know that

Area of square = side ^2

Side ^2 = 4

side = \(\sqrt{4}\)

Side = 2

Hence, The side of the square of each block = 2 feet

Learn more about Area of Square at:

https://brainly.com/question/1658516

#SPJ1

Answer:

Step-by-step explanation:

D

Answer: 12.5%

Step-by-step explanation:

Formula for Half Life

N = N₀ \((\frac{1}{2} ^{\frac{t}{t_{1/2} } } )\)

N = number of isotopes after

N₀ = Initial Isotopes

t = number of years

\(t_{1/2}\) =  half life years

Given

t=6000

\(t_{1/2}\) = 2000

Percent is part out of the whole  = remaining/starting amoung

Percent fraction =  \(\frac{N}{N_{0} }\)

\(\frac{N}{N_{0} } = \frac{1}{2} ^{\frac{t}{t_{1/2} } }\)

\(\frac{N}{N_{0} } = \frac{1}{2} ^{\frac{6000}{2000 } }\)

\(\frac{N}{N_{0} } =\) .125 =12.5%

Answer:

yes they are the same

Step-by-step explanation:

2x + 28 =40

you subtract 28 from both sides

2x + 28 - 28 = 40 - 28

2x=12

divide 12 by 2 and get 6

2(6)=12

2(x + 14)= 40

So, 2(x) + 2(14)

2x + 28 = 40

So they're both the same, just with 2 different ways to solve the same equation...Hope this helps!!

The solution for 2x + 28 = 40 is 6.

The solution for 2(x + 14) = 40 is 6.

Yes, they have the same solution.

Solutions are the values of an equation where the values are substituted in the variables of the equation and make the equality in the equation true.

We have,

2x + 28 = 40

Solve for x.

2x = 40 - 28

2x = 12

x = 6

2(x + 14) = 40

Solve for x.

2x + 28 = 40

2x = 40 - 28

2x = 12

x = 6

Thus,

The solution for both equations is the same.

Learn more about solutions to equations here:

https://brainly.com/question/545403

#SPJ2

The fire is approximately 6.868 miles from Tower A and 7.699 miles from Tower B calculated using trigonometry.

The fire is located 39° east of north from the first observation tower and 42° west of north from the second observation tower. To find the distance to the fire from each tower, we can use trigonometry.

To solve this problem, we can use trigonometry and create a diagram to visualize the situation.

Let's label the first tower as Tower A and the second tower as Tower B. From Tower A, the fire is sighted 39° east of north.

This means that the angle between the direction of the fire and the north direction is 39°.

From Tower B, the fire is sighted 42° west of north.

This means that the angle between the direction of the fire and the north direction is 42°.

Now, let's draw a diagram to represent the situation

In the diagram, the line segment AB represents the distance between the two towers, which is 10 miles.

We need to find the distances x and y, which represent the distances from the fire to Tower A and Tower B, respectively.

Using trigonometry, we can use the tangent function to find x and y.

For Tower A: tan(39°) = x / 10 miles

For Tower B: tan(42°) = y / 10 miles

Let's calculate x and y: x = 10 miles * tan(39°) y = 10 miles * tan(42°)

Using a calculator: x ≈ 6.868 miles y ≈ 7.699 miles

Therefore, the fire is approximately 6.868 miles from Tower A and 7.699 miles from Tower B.

To know more about trigonometry refer here:

https://brainly.com/question/12068045

#SPJ11

Answer:

BD

AC

SN       (might not be one)

AB

Step-by-step explanation:

Answer:

\(B = \frac{g}{m-2g}\)

Step-by-step explanation:

Given

\(g = mB - 2qB\)

Required

Solve for B

\(g = mB - 2qB\)

Factorize the expression

\(g = B(m - 2q)\)

Divide both sides by m - 2g

\(\frac{g}{m-2g} = \frac{B(m - 2q)}{m-2g}\)

\(\frac{g}{m-2g} = B\)

Reorder

\(B = \frac{g}{m-2g}\)

Answer:

h = 61.83 feet

Step-by-step explanation:

length of string from Hector to kite = c = 86 feet.

and 4 feet off the ground.

angle A = 42° 15' 30"

req'd:  how high is the kite?

angle A = 42° + 15' (1° / 60') + 30"(1° / 3600'')

angle A = 42.26

to get the side a (height of kite) 4 feet above ground: use Sin(A) = opp / hyp

Sin(A) = a / c

Sin(42.26) = a / 86

a = Sin(42.26) * 86

a = 57.83 feet

therefore, the height of the kite from the ground = h = 57.83 + 4

h = 61.83 feet

=πr^2h

=π(5)^2*11

=25*11π

=275π yd^3

Graphed in attached file and drawn!

Answer:

see attachment

Step-by-step explanation:

Answer:

Each poet reads for exactly 15 minutes.

Step-by-step explanation:

If it should run for 90 minutes, and there is 6 poets, therefore I'm pretty sure you divide 90 by 6, which is 15.

Answer:

it took him 15 min

Step-by-step explanation:

Let us begin by defining arc measure

Arc measure is a degree measurement, equal to the central angle that forms the intercepted arc.

From the given diagram, we can determine that:

measure of arc DC = 100 degrees

Answer: 100 degrees

Answer:

\(2a^2-5a+3\)

Step-by-step explanation:

2a(a-3)-1(a-3)=

2a^2-6a-a+3=

2a^2-5a+3

Answer:

Step-by-step explanation:

The equation of the output D of Half-subtractor using NOR gate is D = A'B' + AB, a half-subtractor is a digital circuit that performs the subtraction of two binary digits. It has two inputs, A and B, and two outputs, D and C.

The output D is the difference of A and B, and the output C is a borrow signal.

The equation for the output D of a half-subtractor using NOR gates is as follows:

D = A'B' + AB

This equation can be derived using the following logic:

The output D is 1 if and only if either A or B is 1 and the other is 0.

The NOR gate produces a 0 output if and only if both of its inputs are 1.

Therefore, the output D is 1 if and only if one of the NOR gates is 0, which occurs if and only if either A or B is 1 and the other is 0.

The half-subtractor can be implemented using NOR gates as shown below:

A ------|NOR|-----|D

        |      |

B ------|NOR|-----|C

The output D of the first NOR gate is the exclusive-OR (XOR) of A and B. The output C of the second NOR gate is the AND of A and B. The output D of the half-subtractor is the complement of the output C.

The equation for the output D of the half-subtractor can be derived from the truth table of the XOR gate and the AND gate. The truth table for the XOR gate is as follows:

A | B | XOR

---|---|---|

0 | 0 | 0

0 | 1 | 1

1 | 0 | 1

1 | 1 | 0

The truth table for the AND gate is as follows:

A | B | AND

---|---|---|

0 | 0 | 0

0 | 1 | 0

1 | 0 | 0

1 | 1 | 1

The equation for the output D of the half-subtractor can be derived from these truth tables as follows:

D = (A'B' + AB)' = (AB + A'B') = AB + A'B' = A'B' + AB

To know more about equation click here

brainly.com/question/649785

#SPJ11

The distance traveled in the first 5.2 seconds when the speed dropped from the rest as v(t) = 9.8t is equal to 132.496 meters.

'v' is the speed of the object in meter per second

't' is the time in seconds.

Speed dropped from rest 'v(t) = 9.8t '

Distance traveled in the first 5.2 seconds is equal to

= \(\int_{0}^{5.2}\)9.8t dt

= ( 9.8 / 2 )t² \(|_{0}^{5.2}\)

Substitute the lower and upper limit to get the required distance we have,

= 4.9 [ ( 5.2)² - 0² ]

= 4.9 × 27.04

= 132.496 meters

Therefore, the distance traveled for the given first 5.2 seconds is equal to 132.496 meters.

Learn more about distance here

brainly.com/question/15172156

#SPJ4

The above question is incomplete, the complete question is:

Free fall the speed v of an object dropped from rest is given by v(t)=9.8t where v is meters per second and time 't' is in seconds.

(a) Express the distance traveled in the first 5.2 seconds as an integral.

Answer: X=6

Step-by-step explanation:    Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation :

                    6-9*x-(7*x-10*x-30)=0  

Pulling out like terms

1.1     Pull out like factors :

  36 - 6x  =   -6 • (x - 6)  

This equation has no solution.

A a non-zero constant never equals zero.

Solving a Single Variable Equation:

2.2      Solve  :    x-6 = 0  

Add  6  to both sides of the equation :  

                     x = 6

The value of  g(x) = 1/16\(x^{2}\) = (1/4\(x^{2}\)). The correct option is (C).

Given,

In the question:

f(x) = \(x^{2}\)

To find the value of g(x)

To see the graph and analysis

Now, According to the question:

We know that:

g(x) = k f(x) = k\(x^{2}\)

In the graph, The value are given as:

Plug (4,1) into g(x):

1 = k. \(4^2\)

k = 1/16

=> g(x) = 1/16\(x^{2}\) = (1/4\(x^{2}\))

Hence, The value of  g(x) = 1/16\(x^{2}\) = (1/4\(x^{2}\)). The correct option is (C).

Learn more about Graph at:

https://brainly.com/question/17267403

#SPJ1

Answer:

f(3)=21

g(-4)=-14

Step-by-step explanation:

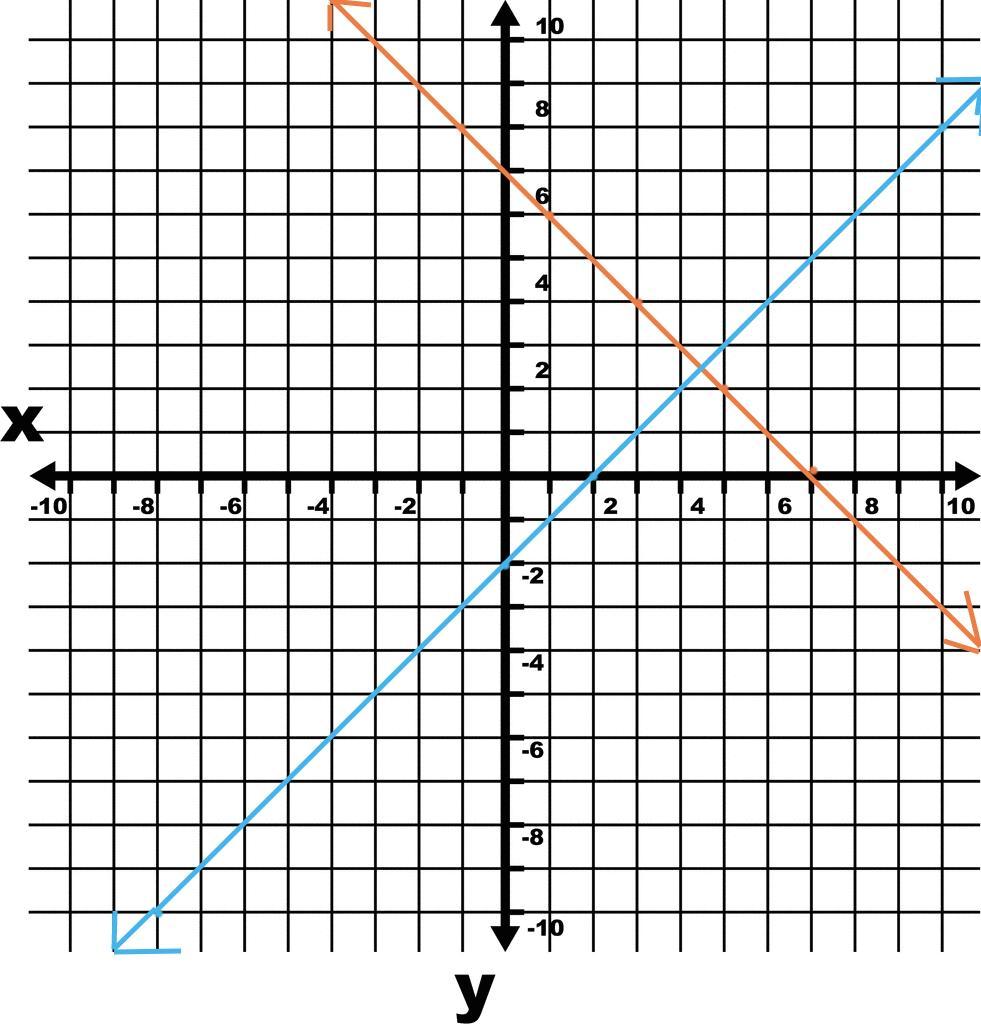
Answer:

Step-by-step explanation:

f(x) = 6x + 3

f(3) =6*3 +3

f(3) = 18 + 3

f(3) = 21

g(x) = 3x - 2

g(-4) = 3*-4 - 2

g(-4) = - 14

f(3)*f(-4) = 21 * -14= -294

The percentage of 322 out of 450 using the percentage formula was found out to be approximately 71.56%.

To find the percentage of 322 out of 450, we can use the following formula:

percentage = (part/whole) x 100

where, "part" is the value we want to express as a percentage (in this case, 322), "whole" is the total value (in this case, 450), and "x" means "multiply".

Using the formula mentioned above, we get:

percentage = (322/450) x 100

percentage = 0.7156 x 100

percentage = 71.56%

Therefore, percentage of 322 out of 450 is approximately 71.56%.

A percentage is a way to express a number as a fraction of 100. It is often denoted using the "%" symbol.

Learn more about percentage here brainly.com/question/16797504

#SPJ4

So the sets A and B, A ⊆ B and B ⊆ A, which implies that A = B.

(a) Let n ∈ A, then n = 8r - 3 for some integer r. We need to show that n is also an element of B, which means that there exists an integer s such that n = 4s + 1.

Since every element of A is also an element of B, we can say that A is a subset of B, i.e., A ⊆ B.

(b) We need to show whether B is a subset of A or not, which means that every element in B must also be an element in A.

Let r = (t + 1) / 2, then we have r is an integer, and

m = 2t - 1 = 2(t+1)/2 - 3 = 2r + 5 - 3 = 8r - 3

Therefore, we have found an integer r (namely, r = (t + 1) / 2) such that m = 8r - 3, which means that m is an element of A.

Since every element of B is also an element of A, we can say that B is a subset of A, i.e., B ⊆ A.

Therefore, we have shown that A ⊆ B and B ⊆ A, which implies that A = B.

Learn more about subset

brainly.com/question/24138395

#SPJ11

Answer:

I think the answer is 7;

Step-by-step explanation:

All i did was subtract Q11 from all 4 of its sides;

11=4=7