14. The number of bottles of water in a pantry after a delivery can be modeled by the
function f(x) = 24x + 35 where x is the number of cases of bottled water delivered.
Which statement is true?
A. Each case of water contains 24 bottles.
B. Each case of water contains 35 bottles.
С. There were 24 bottles of water in the pantry before the delivery.
D. There were 59 bottles of water in the pantry before the delivery.
Answers
The statement "Each case of water contains 24 bottles." is true for f(x) = 24x + 35 where x is the number of cases of bottled water delivered.
What is a function?A relation is a function if it has only One y-value for each x-value.
Given,
The number of bottles of water in a pantry after a delivery can be modeled by the function f(x) = 24x + 35
Where x is the number of cases of bottled water delivered.
We need to find which statement will be true for f(x) = 24x + 35
The statements are:
Each case of water contains 24 bottles.
Each case of water contains 35 bottles.
There were 24 bottles of water in the pantry before the delivery.
There were 59 bottles of water in the pantry before the delivery.
Among the above statements Each case of water contains 24 bottles. the statement is true because as x is the number of cases of bottled water delivered.
Hence Each case of water contains 24 bottles is true statement.
To learn more on Functions click:
https://brainly.com/question/21145944
#SPJ2
Related Questions
What the meaning of "f is order-preserving if x < y implies f(x) < f(y)"?

Answers
An order-preserving function is one where x < y implies f(x) < f(y). An isomorphism is a one-to-one order-preserving function between two partially ordered sets, while an automorphism is an isomorphism of a set to itself.
In the given excerpt, it explains the concepts of order-preserving functions, isomorphisms, and automorphisms in the context of partially ordered sets.
Order-Preserving Function:
A function f: P -> Q, where P and Q are partially ordered sets, is said to be order-preserving if for any elements x and y in P, if x < y, then f(x) < f(y). In other words, the function preserves the order relation between elements in P when mapped to elements in Q.
Increasing Function:
If P and Q are linearly ordered sets, then an order-preserving function is also referred to as an increasing function. It means that for any elements x and y in P, if x < y, then f(x) < f(y).
Isomorphism:
A one-to-one function f: P -> Q is called an isomorphism of P and Q if it satisfies two conditions:
a. f is order-preserving: For any elements x and y in P, if x < y, then f(x) < f(y).
b. f is onto (surjective): Every element in Q has a pre-image in P.
When an isomorphism exists between (P, <) and (Q, <), it means that the two partially ordered sets have a structure that is preserved under the isomorphism. In other words, they have the same ordering relationships.
Automorphism:
An automorphism of a partially ordered set (P, <) is an isomorphism from P to itself. It means that the function f: P -> P is both order-preserving and bijective (one-to-one and onto). Essentially, an automorphism preserves the structure and order relationships within the same partially ordered set.
These concepts are fundamental in understanding the relationships and mappings between partially ordered sets, particularly in terms of preserving order, finding correspondences, and exploring the symmetry within a set.
Learn more about function here:
https://brainly.com/question/11624077
#SPJ8
Hhhhhhheeeellllpppppp asap

Answers
Answer:
Number 1 is 50 and Number 2 is 40
Step-by-step explanation:
25 X 2 = 50
2 X 20 = 40
1 box of blue counters from which 25 counters have been removed and then the remaining number has been doubled
Answers
25-1
24
So remaining there are 24 boxes
And then if the remaining is doubled then
24*2
48 boxes is the answer
-4 (3+8h) =30 round to nearest hundredth
Answers
Answer
-1.31 if its getting rounded to nearest number.
The fraction will be -21/16
what is the solution to the equation below round your answer to two decimal places 7^x=77
A. x = 1.04
B. x = 2.40
C. x = 0.45
D. x = 2.23
Answers
The value of \(7^x = 77\) is C. x = 0.45 obtained by taking log of vase 7 on both sides.
What is a logarithm?The logarithm is exponentiation's opposite function in mathematics.
This indicates that the exponent to which b must be raised in order to obtain a number x is the logarithm of x to the base b. For instance, because 100 = 10², the logarithm of 100 in base 10 is 2, or log10 = 2.
Given, an expression \(7^x = 77\).
Now, \(log_77^x = log_7(77)\).
We have taken log of base 7 on both sides to cancel out log base 7 of 7 to get x explicitly.
\(x = log_777\).
x = 0.4479 Or x = 0.45.
learn more about logarithms here :
https://brainly.com/question/20785664
#SPJ1
What is the correct answer

Answers
In transversal lines, All angles are equal and parallel, so TV ║ WY are parallel lines .
What are transversal lines?
A line that crosses two lines in the same plane at two different geometric locations is referred to as a transversal. Different sorts of angles in pairs, including successive internal angles, corresponding angles, and alternate angles, are produced by a transversal intersection with two lines.A line that crosses other lines is known as a transversal. When transversals intersect parallel lines, such as the two railroad tracks, we often operate with them.∠TUX ≅ ∠UXY ( Alternate angle)
∠SUV ≅ ∠TUX ( Vertically angle)
∠UXY ≅ ∠SUV ( Interior angle )
TV ║ WY ( All angles are equal and parallel, so TV ║ WY
are parallel lines .
Learn more about transversal lines
brainly.com/question/17432060
#SPJ13
4x+5y
order of operations i have been sitting for 3 hours, soooo stuck
Answers
24 + 5(17) = (multiplication)
24 + 85 = (multiplication)
109 (addition).
So, the answer to your equation is 109 when x = 6 and y = 17.
It is expected that 30% of the criminals in our prisons are violent offenders, 65% are nonviolent, and 5% are actually innocent. A sample of 300 inmates showed that 90 were violent offenders, 200 were nonviolent, and 10 were innocent. At the .05 significance level, can we conclude that the observed frequencies are different than the expected frequencies?
Answers
Akshat lost 14 baseball cards from his card collection. He realized that he has lost 28 % of his cards. How many cards were in his card collection initially?
Answers
Answer:
50 cards
Step-by-step explanation:
We can start by saying that his total card collection has x cards in it, meaning that 28% or 28/100 of his total cards, x, is equal to 14. Next, we can divide by 28/100 on both sides, and dividing is the same as multiplying by the reciprocal. The reciprocal of 28/100 is 100/28, so 14 * 100/28 is equal to 100/2, which is 50. We can say that 50 cards were in his card collection initially.
What is a perfect square 6^1
Answers
A perfect square refers to a number that is the result of multiplying an integer by itself. In this case, 6^1 is equal to 6.
However, 6 is not a perfect square because it cannot be obtained by multiplying an integer by itself. The perfect squares up to 6^1 would be 1^2 = 1 and 2^2 = 4.
Leroy prepared 28 kilograms of dough in 7 hours how many hours did Leroy have to work to prepare 40 kilograms of dough
Answers
Leroy would therefore need to put in 10 hours of effort to make the 40 kilos of dough.
What do the digits in kilogram mean?In the World System of Units, a kilogramme serves as the default measure of mass. Since "kilo" is short for "thousand," a kilogramme is equal to 1000 pounds. "kg" is the sign for a kilogramme.
We can start by using a proportion to solve the problem:
kilograms of dough / hours worked = constant rate of dough prepared per hour
Let's call the constant rate of dough prepared per hour "r". We can set up two proportions for the two scenarios:
28 kg / 7 hours = r
40 kg / x hours = r
We want to solve for "x", the number of hours Leroy would need to prepare 40 kg of dough. We can rearrange the second proportion to solve for "x":
x = (40 kg) / (r)
To find "r", we can use the first proportion:
r = (28 kg) / (7 hours) = 4 kg/hour
Now we can substitute "r" into the second proportion and solve for "x":
x = (40 kg) / (4 kg/hour) = 10 hours
Therefore, Leroy would need to work for 10 hours to prepare 40 kilograms of dough.
To know more about Kilogram visit:
https://brainly.com/question/29255021
#SPJ1
A manufacturer has 576 square inches of material available to construct the 6 faces of a carton, which will be in the shape of a rectangular prism. To maximize the volume, the carton will have dimensions such that the length and width are each twice the height.
Answers
To maximize the volume, of the rectangular prism, the carton should have dimensions of approximately 10.74 inches (length), 10.74 inches (width), and 5.37 inches (height).
What is the dimension required to maximize the volume of the box?Assuming the height of the rectangular prism is h inches.
According to the given information, the length and width of the prism will be twice the height, which means the length is 2h inches and the width is also 2h inches.
The total surface area of the rectangular prism is given by the formula:
Surface Area = 2lw + 2lh + 2wh
Substituting the values, we have:
576 = 2(2h)(2h) + 2(2h)(h) + 2(2h)(h)
576 = 8h² + 4h² + 4h²
576 = 16h² + 4h²
576 = 20²
h² = 576/20
h² = 28.8
h = √28.8
h = 5.37
The height of the prism is approximately 5.37 inches.
The length and width will be twice the height, so the length is approximately 2 * 5.37 = 10.74 inches, and the width is also approximately 2 * 5.37 = 10.74 inches.
Learn more on maximizing volume here;
https://brainly.com/question/10373132
#SPJ4
we play a game with a pot and a single die. the pot starts off empty. if the die roll is 1, 2 or 3, i put 1 pound in the pot, and the die is thrown again. if its 4 or 5, the game finishes, and you win whatever is in the pot. if its 6, you leave with nothing.
Answers
Your expected winnings from playing this game are 2 pounds.
What is a game?A game is an activity or a form of play, often with a set of rules and goals, that is undertaken for enjoyment, competition, or skill development.
Let's analyze this game to see what your expected winnings are.
If the first roll is 1, 2, or 3, the game continues and you have a 3 in 6 chance (or 1/2 chance) of continuing to roll the die. Each subsequent roll has the same probabilities and outcomes as the first roll.
Let's start with the case where you win on the first roll with a probability of 1/2. In this case, your winnings are 1 pound.
If you don't win on the first roll, the game continues with a probability of 1/2, and your expected winnings from that point on are the same as your expected winnings from the beginning of the game (since the probabilities and outcomes are the same for all rolls).
Therefore, the expected winnings from the start of the game are:
E = 1/2 * 1 + 1/2 * E
Solving for E, we get:
E = 1 + E/2
E/2 = 1
E = 2
Therefore, your expected winnings from playing this game are 2 pounds.
Learn more about game here : brainly.com/question/26107008
#SPJ1
Complete the Chart.
Rule: +60
___ ___
50 ___
190 ___
425 ___
Answers
Step-by-step explanation:
50 110
190 240
425 485
was this your question?
What is angle
Enter your answer in the box

Answers
Answer:
CAB is 37 degrees
Step-by-step explanation:
90 + 53 = 143
180 - 143 = 37
The following are the temperatures in °C for the first 10 days in January:
1.4, 8.1, 8.2, -5.2, -3.4, -2.3, 8.3, -7.1, 1.3, 3.6
Calculate the range.
Give your answer as a decimal.
Answers
8.2 - - 7.1
8.2 + 7.1 = 15.3
POLS HELP ME NOWWWW I DONT UNDERSTAND IT

Answers
Answer:
B
Step-by-step explanation:
using the equation 'y = 12x', if you plug in zero for 'x' you get zero for 'y'; the only graph that has the point (0, 0) is (b)
also, the x-axis represents time so, as time increases, so does the number of calories burned (which is measured on the y-axis) -- not staying flat or decreasing
Can someone help please?

Answers
Note that where Tom Harris is 24 years old and he wishes to purchase a $7,000 value 10-year term insurance, his annual premium will be: $290.5.
What is Insurance Premium?
Gross premiums written in the insurance sector are the sum of direct and assumed premiums written before subtracting ceded reinsurance. Direct premiums written are the premiums on all policies issued by the company's insurance subsidiaries throughout the fiscal year.
To compute Tom's insurance premium we must use the information given as well as the table above:
Given:
Tom's Age = 24 years
Value of Insurance Cover Requested = $7,000
Type of Insurance cover requested = 10-Year Term
The rate for the Type of Insurance Cover requested: Since he 24 and wants a 10-year term, the rate applicable from the table is; 4.15%
Thus, his annual premium = 7000 * 4.15%
= 29050/ 100
= $290.5
Thus, Tom Harris' annual insurance premium is: $290.5
Learn more about Term Insurance:
https://brainly.com/question/27910991
#SPJ1
If the fractions are 1/6 1/3 1/2 and 2/3 what is the rule for the sequence
Answers
Answer:
66
Step-by-step explanation:
dolars per hour
Krysti is ordering T-shirts for 25 classmates. She knows that 60% of the classmates want the small size. In her order, Kryst mistakenly asked for 12 small shirts. How many small T-shirts
should she have ordered? What was Kryst's error in finding the number of small T-shirts?
Answers
Answer: Krysti's mistake was ordering only 12 small T-shirts when she should have ordered more. To figure out how many small T-shirts she should have ordered, we can start by finding out how many classmates wanted small T-shirts:
60% of 25 classmates = 0.60 x 25 = 15 classmates
So, 15 classmates wanted small T-shirts. If Krysti had ordered one small T-shirt for each of these classmates, she would have needed 15 small T-shirts. However, Krysti only ordered 12 small T-shirts, which means she is short by 3 shirts.
To avoid this mistake, Krysti should have double-checked her calculations and made sure that the number of small T-shirts she ordered matched the number of classmates who wanted small T-shirts.
Step-by-step explanation:
y
is directly proportional to
x
2
.
If
y
=
8
when
x
=
2
find
y
when
x
=
3
Answers
Answer:
y = 18 when x = 3
Step-by-step explanation:
y is directly proportional to x^2, meaning:
\(y=ax^2\)
where a is the proportion between them. We're given the values for both x and y, so plug those in and solve for a:
\(8=a(2)^2\\8=a4\\2=a\\a=2\)
Now you can use a to solve for y when x is 3:
\(y=ax^2\\y=(2)(3)^2\\y=2(9)\\y=18\)
Use S = n^2 to find the sum of 1 + 3 + 5 + . . . + 701.
Answers
Answer:
123201
Step-by-step explanation:
This is an arithmetic sequence of common difference 2 and starting value 1,
So we can use the formula for an arithmetic sequence if we know what is the order of the last term.
Then first use the formula for the nth term to find "n":
\(a_n=a_1+(n-1)d\)
where d = 2, first term = 1 and last term = 701
\(a_n=a_1+(n-1)d\\701=1+(n-1)*2\\700=(n-1)*2\\350=n-1\\n = 351\)
Knowing this, we can estimate the partial sum:
\(S=n\,\frac{a_1+a_n}{2} \\S=351\,\frac{1+701}{2} \\S=351\,*\,351\\S = 123201\)
A straight line is given as 2 x+4 -2 y-5=-3 z-6 (a) Determine the vector equation of the straight line. (b) Find the intersection point between the straight line with the plane yz
Answers
Answer:
a) r(t) = (10, 5, -5) + (5, 5, 0)*t
b) (0, -5, -5)
Step-by-step explanation:
a) 2x + 4 -2y -5 = -3z -6
2x - 2y +3z +5 =0
(10, 5, -5)
(15, 10, -5)
(5, 5, 0)
r = (10, 5, -5) + (5, 5, 0)*t
b) The yz plane is given by the equation x = 0.
x = 0 in the vector equation of a straight line if and only if t = -2, than r ( - 2) = (0, -5, -5) is the desired intersection point.
If the sum of two numbers is 8029, and one of the numbers is 2610, what is the other number?
Answers
Answer:
5419
Step-by-step explanation:
Which values of x are point(s) of discontinuity for this function? Function x = –4 x = –2 x = 0 x = 2 x = 4

Answers
Answer:
x=0 and x=2
Step-by-step explanation:
We need to check at each point where the function changes definition
At x= -2
On the left side -4 on the right side = -( -2)^2 = -4 continuous
At x=0
The point is not defined since neither side has an equals sign
discontinuous
x =2
on the left side 2^2 =4 on the right side 2
It is discontinuous
Answer:
x = 0
x = 2
Step-by-step explanation:
Edge 2020
~theLocoCoco
Find all points on the x-axis that are 16 units from the point (5,-8)
Answers
To find all points on the x-axis that are 16 units away from the point (5, -8), we can use the distance formula. The distance between two points (x₁, y₁) and (x₂, y₂) is given by the formula:
d = √((x₂ - x₁)² + (y₂ - y₁)²)
In this case, the y-coordinate of the point (5, -8) is -8, which lies on the x-axis. So, any point on the x-axis will have a y-coordinate of 0. Let's substitute the given values and solve for the x-coordinate.
d = √((x - 5)² + (0 - (-8))²)
Simplifying:
d = √((x - 5)² + 64)
Now, we want the distance d to be equal to 16 units. So, we set up the equation:
16 = √((x - 5)² + 64)
Squaring both sides of the equation to eliminate the square root:
16² = (x - 5)² + 64
256 = (x - 5)² + 64
Subtracting 64 from both sides:
192 = (x - 5)²
Taking the square root of both sides
√192 = x - 5
±√192 = x - 5
x = 5 ± √192
Therefore, the two points on the x-axis that are 16 units away from the point (5, -8) are:
Point 1: (5 + √192, 0)
Point 2: (5 - √192, 0)
In summary, the points on the x-axis that are 16 units away from the point (5, -8) are (5 + √192, 0) and (5 - √192, 0).
For more such questions on distance formula
https://brainly.com/question/28551043
#SPJ8
HELP ME ASAP PLS. If 19,432 divided by x equals 48 with a remainder of 232. What is X?
Answers
The value of x, given that when it divides a number, there is a quotient and a remainder, is 400
How to find the value of x?To find the value of divisor, we can use a variant of the division algorithm formula :
Divisor = ( Dividend - Remainder ) / Quotient
x is the divisor
Dividend = 19, 432
Remainder = 232
Quotient = 48
This means that the value of x is:
x = ( 19, 432 - 232 ) / 48
x = 19, 200 / 48
x = 400
In conclusion, x is 400.
Find out more on remainder at https://brainly.com/question/19336517
#SPJ1
GIVING BRAINLIST PLEASE HELP!!!
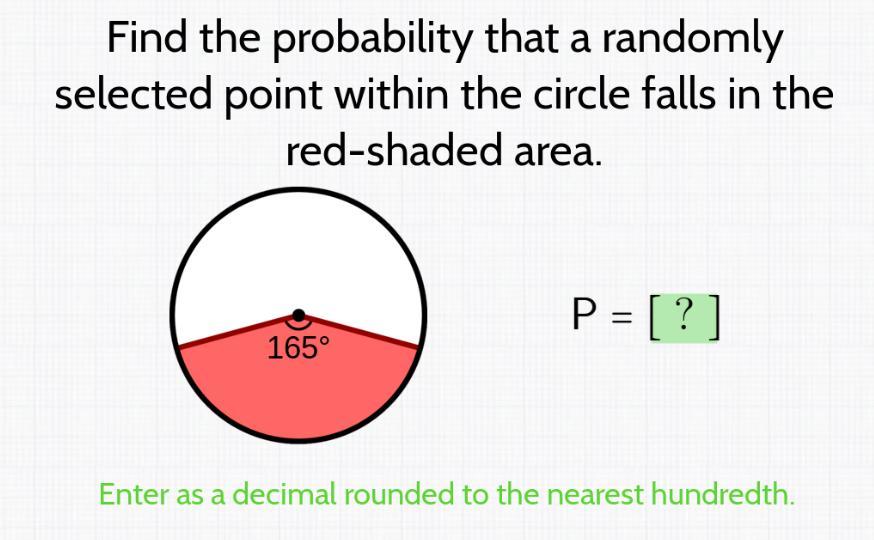
Answers
The probability that a randomly selected point within the circle would fall in the red- shaded area is 45. 833 %
How to find the probability ?The arc that is covered by the red - shaded area in the circle has a degree measure of 165 degrees. This is out of the total circle angle measure of 360 degrees.
This therefore means that the probability that a randomly selected point within the circle would fall in the red- shaded area can be found to be :
= Angle measure of red - shaped area / Total area x 100 %
= 165 / 360 x 100 %
=0. 45833 x 100 %
= 45. 833 %
Find out more on probability at https://brainly.com/question/22690728
#SPJ1
1 mile = 1,760 yards1 yard=3 feetBrody's ran 6 miles to win the race. How many yards did he run?
Answers
Given:
1 mile = 1,760 yards
Brody ran 6 miles to win the race.
Here, we are required to conver 6 miles to yards.
Where,
1 mile = 1760 yards
6 miles = x yards
We have:
\(\frac{6\text{ }\times\text{ 1760}}{1\text{ mile}}=\text{ 10560 yards}\)Therefore, Brody ran 10,560 yards to win the race.
ANSWER:
10,560 yards
2.Sketch the region whose area is given by the integral and evaluate the integral.
3.Evaluate the given integral by changing to polar coordinates.....

Answers
2. The integration region,
\(\left\{(r,\theta)\mid\dfrac\pi6\le\theta\le\dfrac\pi2\land2\le r\le3\right\}\)
corresponds to what you might call an "annular sector" (i.e. the analog of circular sector for the annulus or ring). In other words, it's the region between the two circles of radii \(r=2\) and \(r=3\), taken between the rays \(\theta=\frac\pi6\) and \(\theta=\frac\pi2\). (The previous question of yours that I just posted an answer to has a similar region with slightly different parameters.)
You can separate the variables to compute the integral:
\(\displaystyle\int_{\pi/6}^{\pi/2}\int_2^3r^2\sin^2\theta\,\mathrm dr\,\mathrm d\theta=\left(\int_{\pi/6}^{\pi/2}\sin^2\theta\,\mathrm d\theta\right)\left(\int_2^3r^2\,\mathrm dr\right)\)
which should be doable for you. You would find it has a value of 19/72*(3√3 + 4π).
3. Without knowing the definition of the region D, the best we can do is convert what we can to polar coordinates. Namely,
\(r^2=x^2+y^2\)
so that
\(\displaystyle\iint_De^{x^2+y^2}\,\mathrm dA=\iint_Dre^{r^2}\,\mathrm dr\,\mathrm d\theta\)