15. The average battery life of 2800 manufactured cell phones is recordedand normally distributed. The mean battery life is 12 hours with astandard deviation of 1.0 hours. Find the number of phones whohave a battery life in the 13 to 14 range.*
Answers
Data given;
\(\begin{gathered} \mu=12hrs \\ \sigma=1hr \\ x=13\text{ and 14} \\ Z=\text{?} \end{gathered}\)We have to find the Z score within both ranges, we use the formula below, substituting the given values.
\(\begin{gathered} Z=\frac{x-\mu}{\sigma} \\ Z_{13}=\frac{13-12}{1}=\frac{1}{1}=1 \\ Z_{14}=\frac{14-12}{1}=\frac{2}{1}=2 \end{gathered}\)Since the Z-scores are known, we will get the probability from the Z-score table using the range (1
From the Z-score table, P(1
The number of phones that will have battery life in the 13 to 14 hours range will be;
0.13591 x 2800 = 380.548
Therefore, the number of phones that will have battery life in the 13 to 14 hours range is approximately 381 phones to the nearest whole number since a phone is whole and can not be a fraction.
Related Questions
5.4 times 2 3/4 ???????????????????????????????????????????????????
Answers
Answer: In decimal form, 14.85
Answer in fraction form: 297/20
Step-by-step explanation:
Find the value of the expression below pls help

Answers
Answer:
D 1/16
Step-by-step explanation:
(1/2)^4=.0625
.0625= 1/16
Question is in the picture.

Answers
A formula that describes the average revenue per person is:
average revenue per person = 1.4w
How to find a formula that describes the average revenue per person?Average revenue per person is the ratio of the total revenue received to the number of people. It is calculated by dividing total revenue by the number of people.
We have:
Total revenue formula, M = 350w⁴
Total number of people formula, T = 250w³
Thus,
Average revenue per person = M/T
Average revenue per person = 350w⁴/250w³
Average revenue per person = 1.4w
Learn more about average revenue on:
https://brainly.com/question/29786149
#SPJ1
Matilda uses the polynomial identity (2x−y)^2=4x^2−4xy+y^2 to show that 18² = 324.
What values can Matilda use for x and y?
A . x = 10 and y = 2
B x = 2 and y = 20
C. x = 2 and y = 10
D. x = 20 and y = 2
Answers
The values Matilda use are A. x = 10 and y = 2
Since Matilda uses the polynomial identity (2x−y)² =4x²− 4xy + y² to show that 18² = 324, we choose the value of x = 10 and y = 2 since 2x - y = 2(10) - 2 = 20 - 2 = 18
Substituting the values of the variables into the polynomial identity, we have
(2x − y)² = 4x²− 4xy + y²
(2(10) − 2)² = 4(10)²− 4(10)(2) + 2²
(20 − 2)² = 4(100)− 4(10)(2) + 4
(20 − 2)² = 400 − 80 + 4
18² = 320 + 4
324 = 324
Since both the Left hand side and right hand side of the polynomial equation are equal, then x = 10 and y = 2
So, the values Matilda use are A. x = 10 and y = 2
Learn more about polynomial identities here:
https://brainly.com/question/22054283
A message is coded into the binary symbols 0 and 1 and the message is sent over a communication channel.
The probability a 0 is sent is 0.4 and the probability a 1 is sent is 0.6. The channel, however, has a random error that
changes a 1 to a 0 with probability 0.1 and changes a 0 to a 1 with probability 0.2. Show your work below.
a. What is the probability a 1 is received?
b. If a 1 is received, what is the probability a 0 was sent?
Answers
Answer:
A: the probability that a 1 is received is 0.56.
B: the probability that a 0 was sent given that a 1 is received is (2/25) * (1 - P(0 sent)).
Step-by-step explanation:
To solve this problem, we can use conditional probabilities and the concept of Bayes' theorem.
a. To find the probability that a 1 is received, we need to consider the two possibilities: either a 1 was sent and remained unchanged, or a 0 was sent and got flipped to a 1 by the random error.
Let's denote:
P(1 sent) = 0.6 (probability a 1 is sent)
P(0→1) = 0.2 (probability a 0 is flipped to 1)
P(1 received) = ?
P(1 received) = P(1 sent and unchanged) + P(0 sent and flipped to 1)
= P(1 sent) * (1 - P(0→1)) + P(0 sent) * P(0→1)
= 0.6 * (1 - 0.2) + 0.4 * 0.2
= 0.6 * 0.8 + 0.4 * 0.2
= 0.48 + 0.08
= 0.56
Therefore, the probability that a 1 is received is 0.56.
b. If a 1 is received, we want to find the probability that a 0 was sent. We can use Bayes' theorem to calculate this.
Let's denote:
P(0 sent) = ?
P(1 received) = 0.56
We know that P(0 sent) + P(1 sent) = 1 (since either a 0 or a 1 is sent).
Using Bayes' theorem:
P(0 sent | 1 received) = (P(1 received | 0 sent) * P(0 sent)) / P(1 received)
P(1 received | 0 sent) = P(0 sent and flipped to 1) = 0.4 * 0.2 = 0.08
P(0 sent | 1 received) = (0.08 * P(0 sent)) / 0.56
Since P(0 sent) + P(1 sent) = 1, we can substitute 1 - P(0 sent) for P(1 sent):
P(0 sent | 1 received) = (0.08 * (1 - P(0 sent))) / 0.56
Simplifying:
P(0 sent | 1 received) = 0.08 * (1 - P(0 sent)) / 0.56
= 0.08 * (1 - P(0 sent)) * (1 / 0.56)
= 0.08 * (1 - P(0 sent)) * (25/14)
= (2/25) * (1 - P(0 sent))
Therefore, the probability that a 0 was sent given that a 1 is received is (2/25) * (1 - P(0 sent)).
A message is coded into the binary symbols 0 and 1 and the message is sent over a communication channel. The probability a 0 is sent is 0.4 and the probability a 1 is sent is 0.6. The channel, however, has a random error that changes a 1 to a 0 with probability 0.2 and changes a 0 to a 1 with probability 0.1. (a) What is the probability a 0 is received? (b) If a 1 is received, what is the probability a 0 was sent?
Two part-time instructors are hired by the Department of Statistics and each is assigned at random to teach a single course in probability, inference, or statistical computing. Assume that more than one section of each course is offered. List the outcomes in the sample space [Hint: each element consists of a pair of assignments]. Find the probability that they will teach different courses. Note: carefully define your notation (e.g. any events) in words before solving the problem.
Answers
Answer:
The probability that they will teach different courses is \(\frac{2}{3}\).
Step-by-step explanation:
Sample space is a set of all possible outcomes of an experiment.
In this case we will write the sample space in the form (x, y).
Here x represents the course taught by the first part-time instructor and y represents the course taught by the second part-time instructor.
Denote every course by their first letter.
The sample space is as follows:
S = {(P, P), (P, I), (P, S), (I, P), (I, I), (I, S), (S, P), (S, I) and (S, S)}
The outcomes where the the instructors will teach different courses are:
s = {(P, I), (P, S), (I, P),(I, S), (S, P) and (S, I)}
The probability of an events E is the ratio of the number of favorable outcomes to the total number of outcomes.
\(P(E)=\frac{n(E)}{N}\)
Compute the probability that they will teach different courses as follows:
\(P(\text{Different courses})=\frac{n(s)}{n(S)}=\frac{6}{9}=\frac{2}{3}\)
Thus, the probability that they will teach different courses is \(\frac{2}{3}\).
PLEASE HELP ME, LIKE ACTUALLY! The sum of two numbers is 193. One of them in 71 more than the other. Find the larger of these two numbers
Answers
Answer:
132
Step-by-step explanation:
X is smaller number
x + 71 is larger number.
x+ (x+71)=193
2x = 193-71
2x=122
x=61
x+71=largest number
61+71=132 largest numher
check answer
x+(x+71)=193
61+132=193
Answer:
The larger of the two numbers is 132.
Step-by-step explanation:
let x be the larger number and y be the smaller number.
x + y = 193 [Equatio#1]
x = y +71 [Equation#2]
substitute x from equation #2 into equation # 1:
(y+71) + y = 193
2y = 193 - 71
2y = 122
y = 61
substitute this value of y back into equation #2 to solve for x:
x = (61)+71
x= 132
the larger number is 132.
Jane buys p packets of plain crisps and c packets
of cheese and onion crisps. Write down an
expression for the total number of packets of
crisps Jane buys.
Answers
The expression for the total number of packets of crisps that Jane buys is given as follows:
p + c.
How to obtain the total number of packets?The amounts of packets of crisps purchased are given as follows:
p packets of plain crisps.c packets of cheese and onion crisps.The expression for the total number of packets of crisps that Jane buys is given by the addition of these two amounts.
Hence the expression for the total number of packets of crisps that Jane buys is given as follows:
p + c.
More can be learned about expressions at https://brainly.com/question/13729904
#SPJ1
Which description compares the domains of Function A and Function B correctly? Function A: f(x)=logx Function B: A square root function graphed on a grid in Quadrant One, with the x and y axis beginning at negative ten and increasing in increments of two until reaching ten. The function, labeled g of x, contains a filled in point at begin ordered pair one comma zero end ordered pair and passes through begin ordered pair eight comma two end ordered pair as a smooth curve while extending to infinity. Responses The domain of Function A is the set of real numbers greater than 0. The domain of Function B is the set of real numbers greater than or equal to 1. The domain of Function A is the set of real numbers greater than 0. The domain of Function B is the set of real numbers greater than or equal to 1. The domain of both functions is the set of real numbers greater than or equal to 1. The domain of both functions is the set of real numbers greater than or equal to 1. The domain of Function A is the set of real numbers greater than or equal to 1. The domain of Function B is the set of real numbers greater than 1. The domain of Function A is the set of real numbers greater than or equal to 1. The domain of Function B is the set of real numbers greater than 1. The domain of both functions is the set of real numbers.
Answers
The domain of function A and function B are compared by the statement of Option A: The domain of Function A is the set of real numbers greater than 0. The domain of Function B is the set of real numbers greater than or equal to 1.
What is a function?
A function is a fundamental concept in mathematics that relates a set of inputs (also known as the domain) to a corresponding set of outputs (sometimes referred to as the codomain). For each input, there exists exactly one output, and the output can be linked to its corresponding input in a unique manner.
The domain of a function refers to the set of all possible input values for which the function can produce an output.
In Function A, the domain consists of all real numbers greater than 0, since it is a logarithmic function that can take any positive number as an input.
In contrast, the domain of Function B includes all real numbers greater than or equal to 1, since it is a square root function that begins at (1,0) and continues to infinity.
This means that any number greater than or equal to 1 can be used as an input to produce a corresponding output.
It is essential to define the domain of a function accurately to ensure that the function is well-defined and to avoid potential errors or ambiguities in mathematical computations.
Therefore, the correct statement is A.
To learn more about function from the given link
https://brainly.com/question/2284360
#SPJ1
ASAP!!! NEED AN ANSWER
In this budget scenario, use 15 per hour as the current wage for 40 hour work weeks. Hint: There are 52 weeks in a year, and 12 months in a year.
1. What is the gross yearly income?
2. What is the gross monthly income using this pay rate?
Answers
1)Gross Yearly Income = Hourly Wage × Hours per Week × Weeks in a Year
Gross Yearly Income = $15/hour × 40 hours/week × 52 weeks/year
Gross Yearly Income = $31,200
2)Gross Monthly Income = Gross Yearly Income / Months in a Year
Gross Monthly Income = $31,200 / 12 months
Gross Monthly Income ≈ $2,600
please help 3/4 divided by 1/8
Answers
Answer:
6
Step-by-step explanation:
please help 3/4 divided by 1/8
3/4 : 1/8 =
3/4 x 8 =
24/4 =
6
To show the relationship between the serving size and the number of pounds of meat needed for a lasagna recipe, a catering company uses the chart below.
Lasagna
Serving size Pounds of meat
20 2
40 6
80 8
120 12
The employee who created the chart made an error when computing the number of pounds of meat for one of the serving sizes. For which serving size is the ratio of size to pounds of meat different from the other ratios?
20
40
80
120

Answers
Answer:
The second choice
40
Step-by-step explanation:
All the ratos are 10:1
20/2 = 10/1 ==> 10:1
80/8 = 10/1 ==> 10:1
120/12 =10/1 => 10:1
For a 40 serving size the ratio is
40/6 = 20/3 not equal to 10/1
30 POINTS WILL GIVE BRAINLYEST 2 Questions


Answers
The correct options regarding the statistical measures in this problem are given as follows:
3. The IQR remains a 2.
7. Mean 84º.
What are the quartiles and the IQR of a data-set?To find the quartiles, we need to consider the median, which is the middle value of a data-set, hence:
The first quartile is the median of the first half of the data-set.The third quartile is the median of the first half of the data-set.The interquartile range(IQR) is given by the difference of the two quartiles explained above.For question 3, adding the shoe size of 8, the ordered data-set is given by:
5, 5.5, 6, 6.5, 6.5, 7, 7.5, 8, 8, 8, 8.5.
Hence:
The first half is 5, 5.5, 6, 6.5, 6.5, meaning that Q1 = 6.The second half is 7.5, 8, 8, 8, 8.5, meaning that Q3 = 8.Hence the IQR is given by:
IQR = 8 - 6 = 2.
Thus the correct option is:
The IQR remains a 2.
For question 7, the second lowest value would remain the second highest value. The only measure that considers all the values to be calculated is the mean, hence the correct option is:
Mean 84º.
More can be learned about statistical measures at https://brainly.com/question/24732674
#SPJ1
I’ll give brainliest
Find the area of the smaller sector.
A
Area = [? ]m2
140°
8 m
B
Round your answer to the nearest hundredth.
![Ill give brainliest Find the area of the smaller sector.AArea = [? ]m21408 mBRound your answer to the](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/MCDNbMslS7CggPSqcABthre6OtnlzoPB.png)
Answers
Answer:
Step-by-step explanation:
Remark
Area of an entire circle = pi * r^2
Area of a sector = angle / 360 * pi * r^2
Givens
angle = 140
radius = 8
Solution
Area = (140/360) * 3.14 * 8^2
Area =0.3889 * 3.14 * 64
Area = 78.15
Answer:
78.15
Step-by-step explanation:
22Select the correct answer.Which inequality is graphed on the coordinate plane?

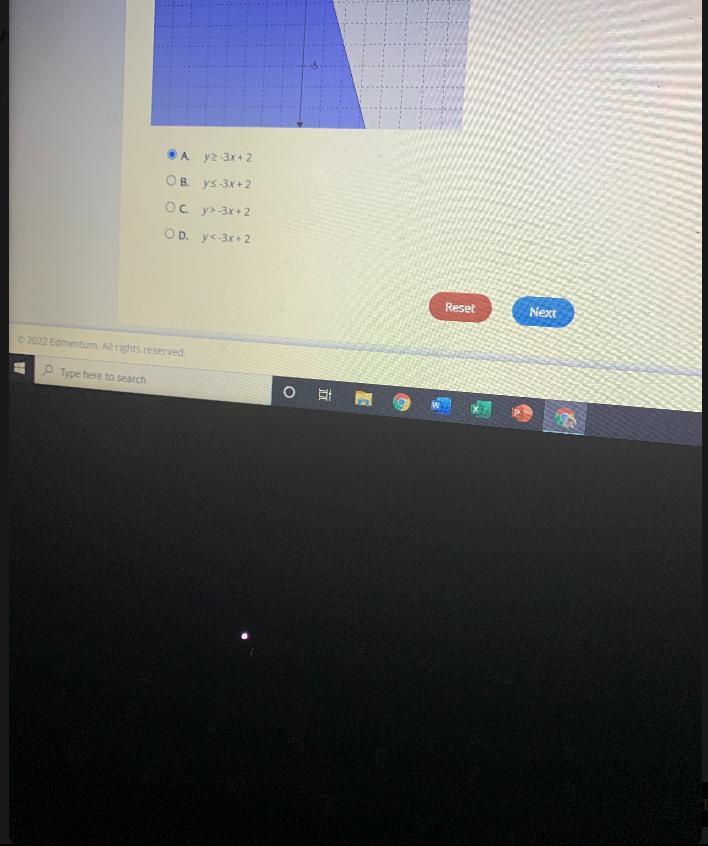
Answers
The line on the graph is a thick line not dashed. This indicates there is an equal to sign attached to the inequality
We only have two options with equal to attached to the inequality
The shading is towards the negative side of y axis (coming down)
So the right option will have a less than and equal to sigh attached:
\(\begin{gathered} \text{The correct inequality:} \\ y\text{ }\le\text{ -3x + 2 (option B)} \end{gathered}\)Oscar’s dog house is shaped like a tent. The slanted sides are both 5 feet long and the bottom of the house is 6 feet across. What is the height of his dog house, in feet, at its tallest point.
Answers
Using Pythagorean theorem, the height of Oscar's dog house, at its tallest point, is approximately 7.81 feet.
What is Pythagorean Theorem?
The Pythagorean Theorem is a fundamental concept in mathematics that relates to the sides of a right triangle. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. The theorem is expressed mathematically as:
a² + b² = c²
Now,
Let's height of the house = "h":
Using Pythagoras
a² + b² = c²
Where "a" and "b" are the lengths of the slanted sides and "c" is the height of the house. We know that "a" and "b" are both 5 feet long, and the bottom of the house is 6 feet across. Let's use this information to find "c":
a = b = 5 feet
b = 6 feet
c² = a² + b²
c² = 5² + 6²
c² = 25 + 36
c² = 61
c = √(61)
c ≈ 7.81 feet
So the height of Oscar's dog house, at its tallest point, is approximately 7.81 feet.
To know more about Pythagorean theorem visit the link
brainly.com/question/343682
#SPJ1
Laura had 32 dollar off coupons for mini golf course but every buddy else had to pay nine dollars per person the full price what was the total cost of their group of eight to play mini golf
Answers
y= 9(8) -32
y= 72-32
y=40
the total cost of their group was $40
mark me brainliest if the answer is correct, thank you in advance :)
Jaden makes 63% of the free throws he shoots. About how many shots do you predict he will have to take to make 15 free throws?
Answers
Answer:
24 shots
Step-by-step explanation:
\(\frac{15}{y}= \frac{63}{100}\)
y × 63 = 15 × 100
63y = 1500
63y ÷ 63 = 1500 ÷ 63
\(y=23\frac{17}{21}\)

What are the coordinates of the midpoint between the points (-1,4) and (2,-5)
Answers
Answer:
(1/2, -1/2)
Step-by-step explanation:
To find a midpoint add the two x's and divide by 2 so -1+2 / 2 = 1/2
add the two y's and divide by 2 so 4-5 / 2 = -1/2
Put the two numbers together as a coordinate (1/2, -1/2)
Question 1 of 10
Which expressions are equivalent to the one below? Check all that apply.
log 2-log 4
A. log(¹)
B. log 1
C. log(2) + log(¹)
D. log 2
Answers
"The correct option is C." The only expression that is equivalent to log 2 - log 4 is option C: log(2) + log(¹).
The expression "log 2 - log 4" can be simplified using logarithmic properties. Specifically, the property states that "log(a) - log(b) = log(a/b)." Applying this property to the given expression, we have "log 2 - log 4 = log(2/4) = log(1/2) = -log(2)."
The expression log 2 - log 4 can be simplified using logarithmic properties. Let's analyze each option:
A. log(¹): This expression is not equivalent to log 2 - log 4. The logarithm of 1 is 0, but it does not cancel out the terms log 2 and log 4.
B. log 1: This expression is equivalent to 0, but it does not cancel out the terms log 2 and log 4.
C. log(2) + log(¹): This expression is equivalent to log 2 + 0, which simplifies to just log 2. It is not equivalent to log 2 - log 4.
D. log 2: This expression is not equivalent to log 2 - log 4. It represents the logarithm of 2, but it does not account for the subtraction of log 4.
Option C, "log(2) + log(¹)," again uses an exponentiation notation without an exponent and is not a valid mathematical expression.
For more such questions on Equivalent:
https://brainly.com/question/2972832
#SPJ8
Triangle DEF is a right triangle. The length of the legs are 7 cm and 10 cm, how long is the hypotenuse? Round to the nearest tenth if possible.
Answers
Answer:
12.2
Step-by-step explanation:
7^2 + 10^2 = C^2
49 + 100 = C^2
149 = C^2
√149 = 12.2
C= 12.2
Using the given information, find the mean, median, and mode.

Answers
To calculate the mean, median, and mode, we first need to know what each of these terms represents. The mean, also known as the average, is the sum of all the values divided by the total number of values. To find the mean, add up all of the values and divide by the number of values. The median is the middle value in a set of data when it is arranged in order from least to greatest. The mode is the value that occurs most frequently in a set of data. Here's an example to illustrate these concepts:
Let's say we have a set of data consisting of the following values: 2, 5, 5, 7, 8, 10, 12. To find the mean, we add up all of the values and divide by the number of values. In this case, the sum of the values is 49 (2+5+5+7+8+10+12) and there are 7 values, so we divide 49 by 7 to get the mean, which is approximately 7. To find the median, we first need to arrange the data in order from least to greatest: 2, 5, 5, 7, 8, 10, 12. The middle value is 7, so that is the median. To find the mode, we look for the value that occurs most frequently. In this case, 5 occurs twice, which is more than any other value, so the mode is 5.
In conclusion, the mean, median, and mode are all measures of central tendency that can be used to describe a set of data. The mean is the average value, the median is the middle value, and the mode is the value that occurs most frequently. When calculating these measures, it is important to carefully consider the data and choose the appropriate method for finding each value.
For such more question on median
https://brainly.com/question/26177250
#SPJ8
Suppose that the number of customers that enter a bank in a hour is a poisson random varialbe, and suppose that P(x=0)=0.07, Determine the mean and variance of x
Answers
The mean and the variance of the poisson distribution are;
Mean = 2.66
Variance = 1.277
How to solve Poisson Distribution problems?The formula for the PMF of a Poisson distribution is;
p(x:λ) = [e^(-λ) * λ^(x)]/x! for x = 0, 1, 2......
Thus;
p(x = 0) = [e^(-λ) * λ^(0)]/0!
e^(-λ) = 0.07
λ = - In 0.07
λ = 2.66
That is the mean
Variance is square root of standard deviation;
Variance = √√(2.66)
Variance = 1.277
Read more about Poisson Distribution at; https://brainly.com/question/9123296
#SPJ1
Answer:
2.65926003693 for mean and variance.
Step-by-step explanation:
First of all, when it comes to Poisson distributions, the mean and variance equal the same thing. Here we can find the mean using e^-(lambda)=0.07 therefore lambda= -ln(0.07) which equals 2.65926003693 for both.
A study suggest 14.7% of all four digit personal identification numbers, or PIN codes, have a repeating digits format such as 2525. Assuming this to be true, if the PIN codes of four people are selected at random, what is the probability that at least one of them will have repeating digits?
Answers
The probability that at least one of the codes will have repeating digits is 0.4712.
What is mean by Probability?The term probability refers to the likelihood of an event occurring. Probability means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one.
Here, The probability of a pin being repeated is 14.7%
⇒ 14.7/100
After Eliminating the decimal point;
⇒ 14.7/100 = 147/1000
Hence,
The probability that a pin, if selected will have a repeating digit format = 147/1000
The probability of a pin not having repeating digits format is,
⇒ 1 - 147/1000
⇒ 853/1000
If four codes are selected at random (without replacement), the probability that all four of the codes will not have repeating digits format is,
⇒ (853/1000) x (852/999) x (851/998) x (850/997)
⇒ 0.5288
Thus, The probability that at least one of them will have repeating digits is,
⇒ 1 - 0.5288
⇒ 0.4712
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ1
I need help on this question

Answers
Answer: i think the answer is A
Step-by-step explanation:i think bc i is a quadratic function
Answer: D
Step-by-step explanation:
A and B don't make sense, since the maximum value > 0, and the function is more negative than positive. C and D are our remaining answers. C would be incorrect, since if X reaches \infinity , the function isn't infinite. The only way to make C correct, is a sudden spike in the function to infinity. So, the only correct answer is D.
Hope this helps (please respond if I'm wrong)
A project has the following projected outcomes in dollars: $230, $340, and $590. The probabilities of their outcomes are 25%, 55%, and 20% respectively. What is the expected value of these outcomes? $362.50 $347.50 $407.50 $377.50
Answers
Answer:
$362.5
Step-by-step explanation:
Given that :
x : _____ 230 ______340 ______ 590
P(x): ____0.25______0.55 _____ 0.20
To obtain the expected value E(x) of the outcome ; we can use the formula :
E(x) = Σ(x * P(x))
E(x) = (230 * 0.25) + (340 * 0.55) + (590 * 0.20)
E(x) = 57.50 + 187 + 118
E(x) = 362.50
#8 i
A parabola with its vertex at (2,5) and its axis of symmetry parallel to the y-axis passes through point (22,365). Write an equation
of the parabola. Then find the value of y when x = 12.
An equation is
Elio Mendoza
When x = 12, y =
Answers
y = a(x - 2)^2 + 5
where a is a coefficient that determines the shape and direction of the parabola.
We can find the value of a by substituting the coordinates of the given point (22, 365) into the equation:
365 = a(22 - 2)^2 + 5
Then, we can solve for a by rearranging the terms and solving for a:
360 = a(20^2)
a = 360 / (20^2)
a = 0.225
Now that we have found the value of a, we can substitute it back into the equation to get the final equation of the parabola:
y = 0.225(x - 2)^2 + 5
To find the value of y when x = 12, we can substitute 12 for x in the equation:
y = 0.225(12 - 2)^2 + 5
y = 0.225(10^2) + 5
y = 2.25 + 5
y = 7.25
Therefore, the value of y when x = 12 is 7.25.
You are taking samples from a normally distributed population with mean 138 and standard deviation 14. Your batch size is 16. Let X-bar be the average of all 16 of your samples. What is the variance of X-bar?
Answers
The variance of X-bar is 12.25.
To find the variance of the sample mean (X-bar) for a normally distributed population, we can use the formula:
Variance of X-bar = (Population Variance) / (Sample Size)
In this case, the population mean (μ) is 138 and the standard deviation (σ) is 14. The population variance (σ^2) can be calculated as the square of the standard deviation, which gives us 14^2 = 196.
Since we are sampling with a batch size of 16, the sample size is also 16.
Now we can substitute these values into the formula:
Variance of X-bar = 196 / 16 = 12.25
Therefore, the variance of X-bar is 12.25.
It's important to note that the sample mean (X-bar) is an unbiased estimator of the population mean (μ). The smaller the sample size, the greater the variability of X-bar around the population mean.
As the sample size increases, the variance of X-bar decreases, indicating a more precise estimate of the population mean.
For more such questions on variance,click on
https://brainly.com/question/9304306
#SPJ8
For Mean = 73.19, Mode = 79.56 and Variance = 16, the Karl Pearson's Coefficient of Skewness will be -0.0256 -1.64 0.0256 0
Answers
Answer:
To calculate Karl Pearson's coefficient of skewness, we need to use the formula:
Skewness = 3 * (Mean - Mode) / Standard Deviation
Given the Mean = 73.19, Mode = 79.56, and Variance = 16, we need to find the Standard Deviation first.
Standard Deviation = √Variance = √16 = 4
Now we can substitute the values into the formula:
Skewness = 3 * (73.19 - 79.56) / 4
Skewness = -6.37 / 4
Skewness = -1.5925
Rounded to four decimal places, the Karl Pearson's coefficient of skewness for the given values is approximately -1.5925.
What is the slope on this graph

Answers
Answer:
-8,4
Step-by-step explanation:
because the slope is slightly 0n 5 and 4