Answers
Answer:
\(\sqrt{269}\)
SIMPLIFIED/ROUNDED: 16.40
Step-by-step explanation:
Use the Pythagorean Theorem to solve for a right triangle: \(a^{2} +b^{2} =c^{2}\)
The legs are "a" and "b".
The hypotenuse (diagonal across from the right angle) is "c".
(In this case, the hypotenuse is XY.)
To start, fill in the values for the formula, then simplify.
\((13)^{2} +(10)^{2} =c^{2}\)
\((169)+(100)=c^{2}\)
\(269=c^{2}\)
Next, take the square root of each side.
\(\sqrt{269} =\sqrt{c^{2} }\)
Taking the square root of c^2 means that the square root and squared (^2) will cancel out, giving you:
\(\sqrt{269} = c\)
Using a calculator (likely the TI-30Xa, most schools use those), round \(\sqrt{269}\) to the nearest tenth (or hundredth). This step isn't needed unless your teacher asks for that.
\(\sqrt{269}\) ≈ 16.40
Related Questions
Identify the phrase that relates to the study of geography.
A. a record of events over time and their meanings
B. the effect living and nonliving things have on each other
C. the creation and use of goods and services
D. the study of rocks and fossils
Answers
Answer:
D
Step-by-step explanation:
Answer:
B
Step-by-step explanation:
I did the test in MIddle school and its in the lesson that's where I found it so next time ur stuck on a question look at the lesson then if your stilll stuck ask brainly k?
Test each of the following series for convergence by the Integral Test. If the Integral Test can be applied to the series, enter CONV if it converges or DIV if it diverges. If the integral test cannot be applied to the series, enter NA. (Note: this means that even if you know a given series converges by some other test, but the Integral Test cannot be applied to it, then you must enter NA rather than CONV.)
1. [infinity]∑n=1 ne−7n
2. [infinity]∑n=1 n+6(−9)n
3. [infinity]∑n=1 ne7n
4. [infinity]∑n=1ln(4n)n
5. [infinity]∑n=1 3nln(5n)
Answers
Convergent in mathematics is a property of approaching a limit more and more explicitly as an argument (variable) of the function increases or decreases or as the number of terms of the series gets increased.
[infinity]∑n=1 ne−7n: The Integral Test can be applied to this series. To use the Integral Test, we need to find an appropriate function whose derivative is positive and increasing and whose series is comparable to the given series. For this series, we can use the function\(f(x) = xe^(-7x)\). Its derivative is f'(x) = \(e^(-7x) - 7xe^(-7x)\) which is positive for x >= 0 and increasing for x >= 0. Moreover, the series [infinity]∑n=1 ne−7n is smaller than the corresponding definite integral, which implies that the series converges. Therefore, the answer is CONV.[infinity]∑n=1 n+6(−9)n: The Integral Test cannot be applied to this series because the terms are not positive. Therefore, the answer is NA.[infinity]∑n=1 ne7n: The Integral Test can be applied to this series. To use the Integral Test, we need to find an appropriate function whose derivative is positive and increasing and whose series is comparable to the given series. For this series, we can use the function\(f(x) = xe^(7x).\) Its derivative is\(f'(x) = e^(7x) + 7xe^(7x)\) which is positive for x >= 0 and increasing for x >= 0. Moreover, the series [infinity]∑n=1 ne7n is larger than the corresponding definite integral, which implies that the series diverges. Therefore, the answer is DIV.[infinity]∑n=1 ln(4n)n: The Integral Test can be applied to this series. To use the Integral Test, we need to find an appropriate function whose derivative is positive and increasing and whose series is comparable to the given series. For this series, we can use the function f(x) = ln(4x). Its derivative is f'(x) = 1/x which is positive and increasing for x >= 1. Moreover, the series [infinity]∑n=1 ln(4n)n is smaller than the corresponding definite integral, which implies that the series converges. Therefore, the answer is CONV.[infinity]∑n=1 3nln(5n) : The Integral Test can be applied to this series. To use the Integral Test, we need to find an appropriate function whose derivative is positive and increasing and whose series is comparable to the given series. For this series, we can use the function f(x) = 3xln(5x). Its derivative is f'(x) = 3ln(5x) + 9 which is positive for x >= e^(3/9). Moreover, the series [infinity]∑n=1 3nln(5n) is smaller than the corresponding definite integral, which implies that the series converges. Therefore, the answer is CONV.For more such questions on convergence
https://brainly.com/question/15369696
#SPJ4
a box with a square base and open top must have a volume of . we wish to find the dimensions of the box that minimize the amount of material used. first, find a formula for the surface area of the box in terms of only , the length of one side of the square base. simplify your formula as much as possible. next, find the derivative, .
Answers
The formula for the surface area of the box, in terms of the length of one side of the square base (s), is A = s^2 + 4s^2 = 5s^2.
The derivative of the surface area function with respect to s, denoted as dA/ds, gives us the rate of change of the surface area with respect to the length of one side of the base.
1. The surface area of the box consists of the area of the square base and the four equal sides. The area of the square base is s^2, and each side has a length of s. Therefore, the total surface area is given by A = s^2 + 4s^2 = 5s^2.
2. To find the derivative of the surface area function, we differentiate 5s^2 with respect to s using the power rule of differentiation. The power rule states that if we have a function f(x) = cx^n, then the derivative is f'(x) = cnx^(n-1).
Applying the power rule, we have dA/ds = d(5s^2)/ds = 10s.
3. The derivative, dA/ds = 10s, represents the rate of change of the surface area with respect to the length of one side of the square base. This means that for every unit increase in s, the surface area increases by 10s units.
The derivative does not provide information about minimizing the amount of material used. To find the dimensions of the box that minimize the amount of material used, we need to set up an optimization problem and solve for the critical points. This involves setting the derivative equal to zero and finding the values of s that satisfy this equation. However, since the problem statement does not provide a specific volume constraint or objective function, we cannot proceed with the optimization process.
To learn more about derivative, click here: brainly.com/question/23819325
#SPJ11
Which of the following best describes the equation below?
y = -2x2 - 4
A.
both linear and nonlinear
B.
neither linear nor nonlinear
C.
nonlinear
D.
linear
Answers
Answer:
I think it's C nonlinear
Step-by-step explanation:
Answer:
d
Step-by-step explanation:
use desmos calculator helps with these question
Simplify: 4b^5 + 10b^5
Answers
Answer:
14 b^5
Step-by-step explanation:
you can do all mathmatical operations to same variables with same power
alfred and bonnie play a game in which they take turns tossing a fair coin. the winner of a game is the first person to obtain a head. alfred and bonnie play this game several times with the stipulation that the loser of a game goes first in the next game. suppose that alfred goes first in the first game, and that the probability that he wins the sixth game is m n , where m and n are relatively prime positive integers. what are the last three digits of m n ? (1993,
Answers
So, the last three digits of m*n is 001.
Let p be the probability that Alfred wins given that he goes first. Then, the probability that Bonnie wins given that she goes first is 1-p. Therefore, the probability that Alfred wins the second game given that Bonnie went first in the first game is 1-p. Similarly, the probability that Alfred wins the third game given that he went first in the second game is p, and so on.
Therefore, the probability that Alfred wins the sixth game given that he went first in the first game is:
p(1-p)(1-p)(p)(p)(p) = p^4 (1-p)^2
Since m and n are relatively prime, the last three digits of m*n are the last three digits of p^4 * (1-p)^2, which is the last three digits of p^4 and the last three digits of (1-p)^2. Since p is the probability of winning given that you go first, it is a number between 0 and 1. Therefore, the last three digits of p^4 and (1-p)^2 are 001, resulting in the last three digits of the final answer being 001.
Therefore, the last three digits of m*n is 001.
To learn more about probability
Visit; brainly.com/question/28525447
#SPJ4
This is precalc trig please help

Answers
The answer to the trigonometry question in the picture attached is:
= cos θ / [sin θ * (1 - sin θ)] * (1 + sin θ)
Here is the step by step approach to solving the trigonometrySimplify 1-csc θ as follows:
1 - csc θ = (1 - csc θ)(1 + csc θ) / (1 + csc θ)
= 1 - csc^2 θ / (1 + csc θ)
= 1 - 1/sin^2 θ / (1 + 1/sin θ)
= 1 - sin^2 θ / (sin θ + 1)
= (sin θ - sin^2 θ) / (sin θ + 1)
Simplify 1+csc θ as follows:
1 + csc θ = (1 + csc θ)(1 - csc θ) / (1 - csc θ)
= 1 - csc^2 θ / (1 - csc θ)
= 1 - 1/sin^2 θ / (1 - 1/sin θ)
= 1 - sin^2 θ / (sin θ - 1)
= (sin θ + sin^2 θ) / (sin θ - 1)
Substitute the above simplifications in the expression cos θ/(1-csc θ) * 1+csc θ/(1+ csc θ) to get:
cos θ / (sin θ - sin^2 θ) * (sin θ + sin^2 θ) / (sin θ + 1)
Simplify the expression by canceling out the sin^2 θ terms:
cos θ / (sin θ - sin^2 θ) * (sin θ + sin^2 θ) / (sin θ + 1)
= cos θ / (sin θ - sin^2 θ) * (1 + sin θ) / (sin θ + 1)
Simplify further by factoring out common terms in the numerator and denominator:
cos θ / (sin θ - sin^2 θ) * (1 + sin θ) / (sin θ + 1)
= cos θ * (1 + sin θ) / [(sin θ - sin^2 θ) * (sin θ + 1)]
Finally, simplify the expression by factoring out a sin θ term from the denominator:
cos θ * (1 + sin θ) / [(sin θ - sin^2 θ) * (sin θ + 1)]
= cos θ * (1 + sin θ) / [sin θ * (1 - sin θ) * (sin θ + 1)]
= cos θ / [sin θ * (1 - sin θ)] * (1 + sin θ)
Learn more about Trigonometry here:
https://brainly.com/question/25618616
#SPJ1
what coefficient would you get for the x terms on the right side of 3x+15=2x+10+x+5
Answers
Answer:
x=0
Step-by-step explanation:
Answer:
Any real number.
Step-by-step explanation:
3x + 15 = 2x + 10 + x + 5
First, add like terms.
3x + 15 = 3x + 15
Subtract 15 on both sides.
3x = 3x
Divide 3 on both sides.
x = x
Since x equals x, you can give any value (any real number) to x.
Since 3x = 3x, you can say x = 1, meaning 3 = 3.
Or, you can say x = 8. 3x = 3x will be 24 = 24.
x can be any number.
I am really behind and I REALLY need help... I am giving every point I have for this...


Answers
Answer:
Get ahead then
Step-by-step explanation:
Step-by-step explanation:
Shorts cost $16
T-shirts cost $10
So:
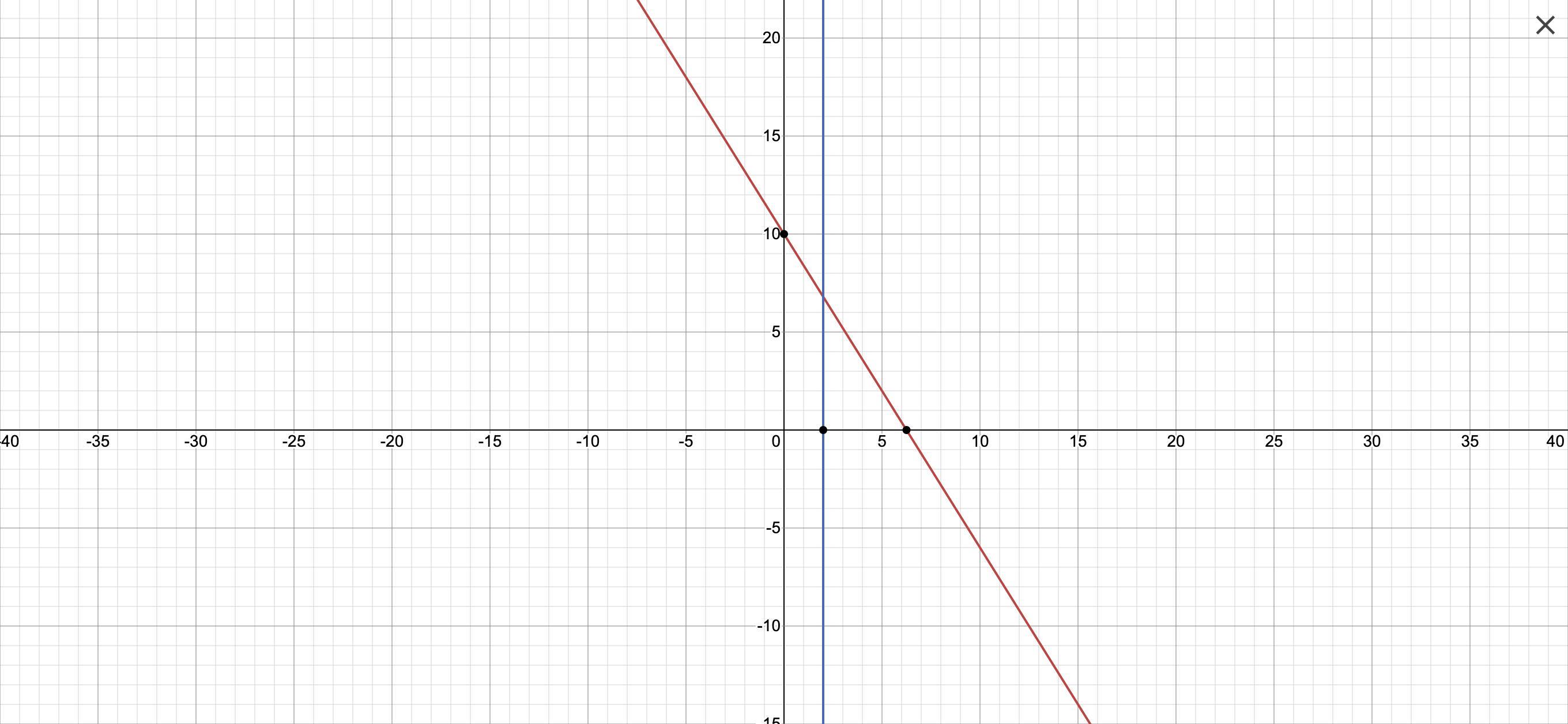
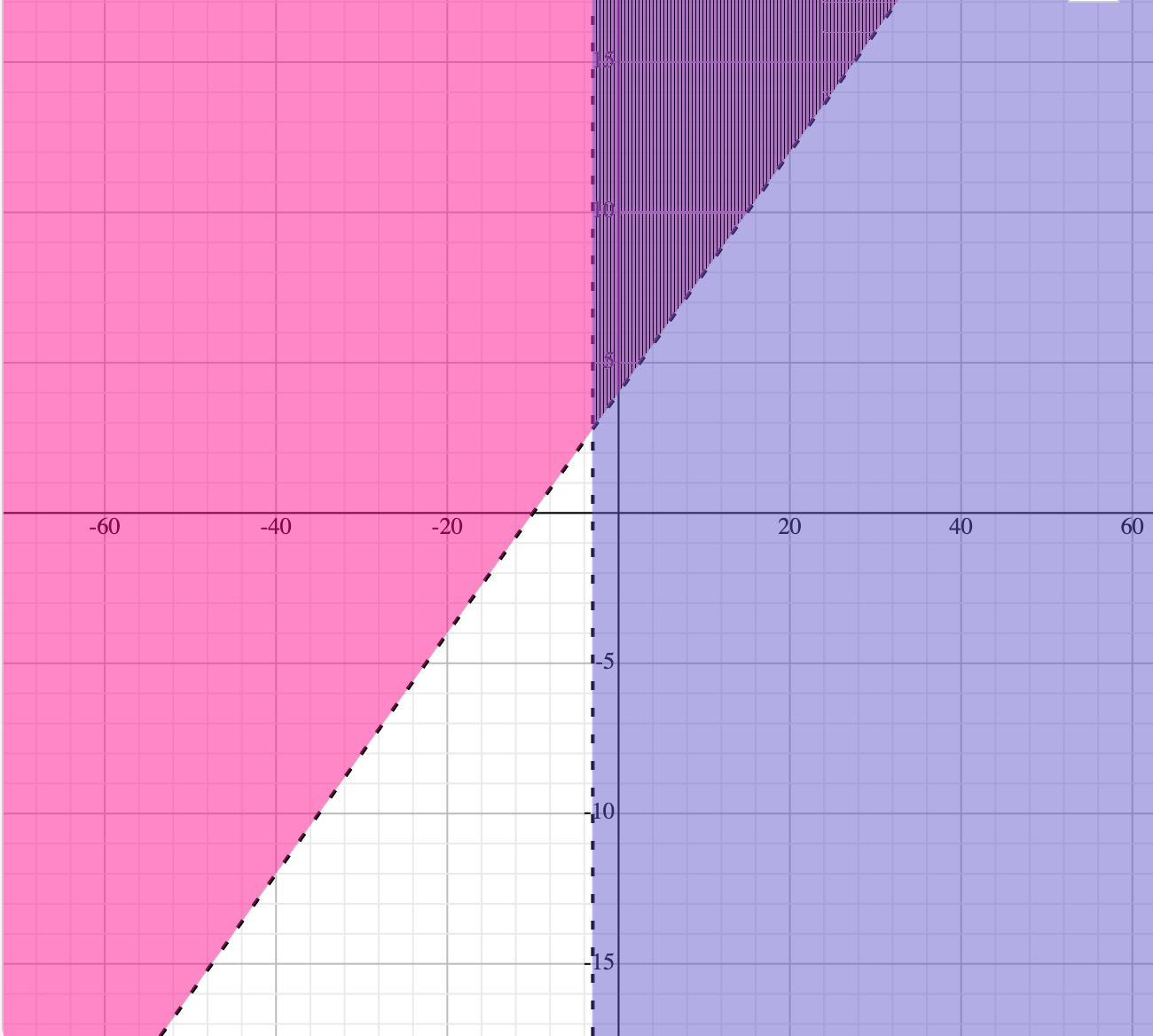
16x + 10y ≤ 100
or
y ≤ -1.6x + 10
Then graph y = -1.6x + 10 and x = 2
Part b:
Using the graph, we can infer that there are two possible solutions:
A. 3 pairs of shorts and 4 t-shirts
B. 4 pairs of shorts and 2 t-shirts
6a. X = number of apples, Y = number of oranges
So:
x + y ≤ 20
0.24x + 0.8y ≤ 12
x ≤ 20 - y
0.24(20 - y) + 0.8 ≤ 12
= 4.8 - 0.24y + 0.8y ≤ 12
= 0.56y ≤ 7.2
y = 12.9 (You can use twelve because there can't be a fraction of an orange.)
x = 7.14 (again, because of fractions, round to 7.)
Therefore, she got 12 oranges and 7 apples.
Part 2:
Question 1:
Both equations are unbounded.
Question 2:
Both equations are unbounded.
Question 3:
Both equations are unbounded.
Question 4:
Both equations are unbounded.
Give me a moment to add question four's graph.



if v × w = 6 i − 7 j 9k, and v · w = 9, find tan where is the angle between v and w.
Answers
The tangent of the angle between vectors v and w is 2√(21) / 9
We can use the dot product and cross-product formulas to find the angle between two vectors.
The dot product of two vectors v and w is given by:
v · w = ||v|| ||w|| cos(θ)
where ||v|| and ||w|| are the magnitudes of the vectors v and w, and θ is the angle between them.
The cross product of two vectors v and w is given by:
v × w = ||v|| ||w|| sin(θ) k
where k is a unit vector in the direction of the cross product.
Since v × w = 6i - 7j + 9k and v · w = 9, we can find the angle between v and w as follows:
\(\theta = sin^{-1}\frac{||v \times w||}{||v|| \ ||w||} = sin^{-1}\frac{||6i - 7j + 9k||}{||v|| \ ||w||}\)
We can find the magnitude of v × w by using the formula for the magnitude of a cross-product:
\(||v \times w|| = ||6i - 7j + 9k|| \\\\= \sqrt{6^2 + (-7)^2 + 9^2} = \sqrt{6^2 + 49 + 9^2}\\\\=\sqrt{84} = \sqrt(2^2 \times 3 \times 7) = 2\sqrt{(3 \times 7)\)
We can find the magnitude of v and w using the given dot product formula:
v · w = ||v|| ||w|| cos(θ) = 9
||v|| ||w|| = 9 / cos(θ)
Since we know that ||v|| and ||w|| are positive, we can square both sides to obtain:
\((||v|| \ ||w||)^2 = \frac{9 }{cos(\theta))^2} \\\\||v||^2 \ ||w||^2 = \frac{81}{cos^2(\theta)}\)
Finally, using the tangent formula, we can find tanθ:
tan(θ) = sin(θ) / cos(θ) = ||v × w|| / ||v·w|| = 2√(3 × 7) / 9 = 2√(21) / 9.
To learn more about the vectors, visit:
brainly.com/question/24256726
#SPJ4
I really really need help with this and no one is answering. I've looked everywhere for how to do this and I fell like its simple but I can't find it. given -2+4i, express the complex number in polar form. I know the answer is 2 root 5(cos2.03 + isin2.03), but I don't know where the 2.03 comes from. Can someone explain please?
Answers
Result:
Complex number:
The polar form of z is:
Explanation:
z = −2 + 4i
z = 4.4721 · (cos 117o + i · sin 117o)
The polar form of the complex number z = a + bi is:
z = r · (cos θ + i · sin θ)
where, r is the modulus of z and θ is an argument of z. The moduo for a = −2 and b = 4 is:
r = a2 + b2 = · · · = 4.4721 To find argument θ we use one of the following formulas:
b θ=arctan a ifa>0
b o θ=arctan a +180 ifa<0
θ=90o ifa=0andb>0 θ=270o ifa=0andb<0
Inthisexample: a=−2andb=4so:
θ=arctan a +180
θ=arctan 4 +180o −2
b o
θ = arctan (−2) + 180o θ ≈ 117o
Try this website it’s really helped me!
www.mathportal.org/calculators/complex-numbers-calculator/complex-unary-operations-calculator.php?val1=-2&combo1=1&val2=4&rb1=pol&ch2=useDecimals
Answer:
Step-by-step explanation:
a+bi = -2+4i
arctan(b/a)=arctan(4/-2)=-1.071
Because this falls in quardant 2, you have to add pi
1.071+pi=2.03
I hope this helps.
If f(x)=16x-30 and g(x)=14x-6, for which value of x does (f-g)(x)=0?
12
13
14
Answers
The value of x for which (f - g)(x) = 0 is x = 12.
To find the value of x for which (f - g)(x) = 0, we need to subtract g(x) from f(x) and set the resulting expression equal to zero. Let's perform the subtraction:
(f - g)(x) = f(x) - g(x)
= (16x - 30) - (14x - 6)
= 16x - 30 - 14x + 6
= 2x - 24
Now, we can set the expression equal to zero and solve for x:
2x - 24 = 0
Adding 24 to both sides:
2x = 24
Dividing both sides by 2:
x = 12
Therefore, the value of x for which (f - g)(x) = 0 is x = 12.
Know more about the expression click here:
https://brainly.com/question/15034631
#SPJ11
At theage of 27, to save for retirement, you decibe to deposit %50 at the end of each month in an IRA that pays 5% compounded monthly.
a. Use the following formula to determine how much you will have in the IRA when you retire at age 65.
A= P[(1+r)^t-1] / r or A=P[(t=r/n)^nt-1 / (r/n)
b. Find the interest
Answers
Interest = A - (50 * 456)
To determine how much you will have in the IRA when you retire at age 65, we can use the formula A = P[(1 + r)^t - 1] / r, where A is the future value, P is the monthly deposit, r is the monthly interest rate, and t is the number of months.
a. In this case, the monthly deposit is 50, the monthly interest rate is 5% or 0.05, and the number of months is (65 - 27) * 12 = 456 (from age 27 to 65).
Using the formula, we can calculate:
A = 50[(1 + 0.05)^456 - 1] / 0.05
b. To find the interest, we can subtract the total deposits from the future value:
Interest = A - (P * t)
In this case:
Interest = A - (50 * 456)
To learn more about Interest
https://brainly.com/question/30393144
#SPJ11
HELp MeEeeEEE!!!
I will give Brainliest!!

Answers
Answer:
1: the answer is 6x
2: its 39
Step-by-step explanation:
for 1 I I used 8 x X = 8x - 2 = 6x.
for 2 all I did was substrac 3 out of 42 which gave me 39
Good luck
let be a uniform (0,1) random variable. to construct a random variable =() so that has the cdf , take = ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ .
Answers
Construct a random variable Y from a uniform (0,1) random variable X to achieve a specific CDF.
The exact form of the inverse CDF and the resulting random variable Y will depend on the specific desired CDF F(y). By using the inverse CDF method, we can transform the uniform random variable into a new random variable with the desired distribution.
To construct a random variable Y from a uniform (0,1) random variable X, such that Y has a specific cumulative distribution function (CDF), we can use the inverse CDF method. The inverse CDF method involves finding the inverse of the desired CDF and applying it to the uniform random variable X.
In this case, let F(y) be the desired CDF. To construct Y with CDF F(y), we take Y = F^(-1)(X), where F^(-1) denotes the inverse of the CDF F.
By taking the inverse of the desired CDF F(y) and applying it to the uniform random variable X, we obtain the random variable Y that has the desired CDF.
To learn more about variable click here:
brainly.com/question/15078630
#SPJ11
Kieran and Louise each think of a number.
4 less than Kieran's number is equal to 2 lots of Louise's
number.
3 lots of Kieran's number added to Louise's number is 68.
Using the information above, write and solve two
simultaneous equations to work out Kieran and Louise's
numbers.
Answers
Using simultaneous equations, Kieran and Louise's numbers are 20 and 8 respectively.
How to represent situation with system of equation?Kieran and Louise each think of a number. 4 less than Kieran's number is equal to 2 lots of Louise's number.
let's
x = Kieran's number
y = Louise's number.
x - 4 = 2y
x - 2y = 4
3 lots of Kieran's number added to Louise's number is 68.
Hence,
3x + y = 68
Hence, let's combine the system of equation.
x - 2y = 4
3x + y = 68
multiply equation(i) by 3
3x - 6y = 12
3x + y = 68
-7y = -56
y = -56 / -7
y = 8
Therefore, let's find x
x = 4 + 2y
x = 4 + 2(8)
x = 4 + 16
x = 20
Hence,
Kieran number = 20
Louise number = 8
learn more simultaneous equation here: https://brainly.com/question/29272080
#SPJ1
Solve for x. Assume that lines which appear to be tangent are tangent.

Answers
Answer:
7)
\(\tt 2x-14=x-2\)
\(\tt 2x-x=14-2\)
\(\boxed{\tt x=12}\)
~
8)
\(\tt -6+7x=5x+10\)
\(\tt 7x-5x=6+10\)
\(\boxed{\tt x=8}\)
~
9)
\(\tt x-2=2x-6\)
\(\tt 6-2=x\)
\(\boxed{\tt x=4}\)
~
10)
\(\tt 2x+10=4x-10\)
\(\tt 4x-2x=10+10\)
\(\tt 2x=20\)
\(\boxed{\tt x=10}\)
~
11)
\(\tt 5x+7=4x+15\)
\(\tt 5x-4x=15-7\)
\(\boxed{\tt x=8}\)
~
12)
\(\tt 12x=11x+2\)
\(\tt 12x-11x=2\)
\(\boxed{\tt x=2}\)
~
A fitness center charges $3 per visit plus a monthly fee of $30. How much would it cost in one month if Ella has 18 visits?
$48
$54
$84
$90
Answers
Answer:
84$
Step-by-step explanation:
It says it costs $3 per visit and Ella went 18 times
So we can describe that as x represents the times she has visited, x=18, so 3(18)
now we just add $30 dollars since she only went in one month and $30 is the fee per month so that would be (3*18=) 54+30
which would then give you $84 dollars!
hope it helps!!
Answer:
C.) $84
Step-by-step explanation:

Calculate 9[divided]1/3
A.9/3
B.3/9
C.13 1/2
D.27
Please help me.
Answers
Answer: I believe the answer would be B
Step-by-step explanation:
\(\qquad\qquad\huge\underline{{\sf Answer}}\)
Let's evaluate ~
\(\qquad \tt \dashrightarrow \:9 \div \frac{1}{3} \)
\(\qquad \tt \dashrightarrow \:9 \times3\)
\(\qquad \tt \dashrightarrow \:27\)
so, the correct choice is D. 27
What is 5n = 185 what’s the n=__?
249 = 3y y=__?
-6w = 354 w=__?
Answers
1. n = 37
isolate n by dividing both sides by 5
2. y = 83
isolate y by dividing both sides by 3
3. w = -118
isolate w by dividing both sides by -6
i’ll give you brainliest.. which situation best represents the equation below?

Answers
Answer:
I think it is C
Step-by-step explanation:
Answer:
C
Step-by-step explanation:
When Landon moved into a new house he planted two trees in his backyard. At the time of planting tree a what 24 inches tall and tree B was 40 inches tall. Each year there after three A grew by 9 inches per year and tree B grew by 5 inches per year. Let A represent the height of tree A t years after being planted and let B represent the heights of tree B t years after being planted. Write an equation for each situation in terms of t, and determine the height of both trees at the time when they have an equal height.
Answers
Answer:
A=24+9t
B=40+5t
Step-by-step explanation:
see attached

Kyle used 9 as An estimate for 3 1/6 + 5 7/8. He got 9 1/24 for the exact sum. Is his calculated answer reasonable? Explain
Answers
Kyle's estimate of 9 was not very accurate, but his calculated answer of 9 1/24 is a reasonable approximation of the sum.
To determine if Kyle's calculated answer is reasonable, we can compare it to the original sum of 3 1/6 + 5 7/8.
First, we need to convert the mixed numbers to improper fractions:
3 1/6 = 19/6
5 7/8 = 47/8
Next, we can add the fractions:
19/6 + 47/8 = (152 + 141)/48 = 293/48
Now, we can compare this exact sum to Kyle's estimated answer of 9 and his calculated answer of 9 1/24.
Kyle's estimated answer of 9 is much larger than the exact sum of 6 5/48.
Thus, Kyle's estimate of 9 was not very accurate, but his calculated answer of 9 1/24 is a reasonable approximation of the sum.
Learn more about the estimation here:
https://brainly.com/question/13486890
#SPJ4
Four more than the product of a number and 8 is equal to 7.
Answers
Answer: x = 0.375
Step-by-step explanation:
Equation: 8x + 4 = 7
Subtract 4 on both sides
8x = 3
Divide by 8 on both sides
x = 3/8 is 0.375 decimal
x = 0.375 (0.38 round-up)
Answer:
x = 3/8
Step-by-step explanation:
Four more than the product of a number and 8 is equal to 7.
4 + 8x = 7
8x = 7 - 4
8x = 3
x = 3/8
---------------------
check
4 + 8 x 3/8 = 7
4 + 3 = 7
7 = 7
the answer is good
A Honda dealership sells both motorcycles and cars.there are a total of 200 vehicles on the dealership's lot. the detailer cleaned all the wheels of all the vehicles, which totaled 698 wheels. how many motorcycles and cars are there on the lot?
Answers
Answer:
x = 149, cars and 51 motorcyles
Step-by-step explanation:
4x + 2(200-x) = 698
2x = 298 x = 149, cars and 51 motorcyles
40000$ consumer loan will be paid in monthly equal installment over
2years monthly payments , if the interest rate is 15.8% what will
be the amount?
Explain the answer in details
Answers
A consumer loan of $40,000 with a 15.8% interest rate will require monthly payments over a period of 2 years. The total amount to be paid, including both principal and interest, will be approximately $45,380.
To calculate the monthly payments, we need to determine the total amount to be paid over the loan period, including the principal amount and the interest. The formula used for calculating equal monthly installments is:
M = P * (r * (1 + r)^n) / ((1 + r)^n - 1)
Where:
M = Monthly payment
P = Principal amount
r = Monthly interest rate
n = Number of monthly payments
In this case, the principal amount (P) is $40,000, the interest rate (r) is 15.8% per year, and the loan duration (n) is 2 years (24 months).
First, we convert the annual interest rate to a monthly rate by dividing it by 12: 15.8% / 12 = 0.0132.
Next, we substitute the values into the formula:
M = 40,000 * (0.0132 * (1 + 0.0132)^24) / ((1 + 0.0132)^24 - 1)
Calculating this formula gives us the monthly payment (M) of approximately $1,907.42.
To find the total amount to be paid, we multiply the monthly payment by the number of payments: $1,907.42 * 24 = $45,778.08. However, this includes both the principal and the interest. Subtracting the principal amount ($40,000) gives us the total interest paid: $45,778.08 - $40,000 = $5,778.08.
Therefore, the total amount to be paid, including both principal and interest, will be approximately $45,778.08.
To learn more about interest click here: brainly.com/question/30393144
#SPJ11
12=6-90
asap please xoxo!!!!!!
Answers
answer:
72
step-by-step explanation:
your question doesn't make mathematical sense how can 12 = 6 then subract 90?
maybe you meant 12 + 6 - 90
if so
the answer is
72
(my work)
12 + 6 = 18
18 - 90 = 72
hope this helped <3
pls answer with equation

Answers
Answer:
127°
Step-by-step explanation:
171+62+127=360
Answer:
x=127°
Step-by-step explanation:
x+171° +62=360°
x=360°-(171°+62°)
x=127°
Please help me solve the question from below. It is from IM3 Algebra

Answers
The equation log₂(x - 1) = x³ - 4x has one solution at x = 2.
To determine the solutions to the equation log₂(x - 1) = x³ - 4x, we can set the two expressions equal to each other:
log₂(x - 1) = x³ - 4x
Since we know that the graphs of the two functions intersect at the points (2, 0) and (1.1187, -3.075), we can substitute these values into the equation to find the solutions.
For the point (2, 0):
log₂(2 - 1) = 2³ - 4(2)
log₂(1) = 8 - 8
0 = 0
The equation holds true for the point (2, 0), so (2, 0) is one solution.
For the point (1.1187, -3.075):
log₂(1.1187 - 1) = (1.1187)³ - 4(1.1187)
log₂(0.1187) = 1.4013 - 4.4748
-3.075 = -3.0735 (approx.)
The equation is not satisfied for the point (1.1187, -3.075), so (1.1187, -3.075) is not a solution.
Therefore, the equation log₂(x - 1) = x³ - 4x has one solution at x = 2.
Learn more about Logarithm here:
https://brainly.com/question/30226560
#SPJ1
9.0 divided by 18 what is the answer?
Answers
Answer: 0.9 divided by 18 is 0.05.
Step-by-step explanation:
