1
Three times the measure of a supplement of an angle is eight times the measure of a complement of the angle. What is the measure of the angle?
Type in the number only
The measure of the angle is
Answers
Answer:
The measure of the angle is 36°
Step-by-step explanation:
Let the measure of angle be x
Supplementary angles : A pair of angles whose sum is 180° is called supplementary angles
So, Supplement of x = 180°-x°
Complementary angles A pair of angles whose sum is 90° is called complementary angles
So, Complement of x = 90°-x°
We are given that Three times the measure of a supplement of an angle is eight times the measure of a complement of the angle
So, 3(180-x)=8(90-x)
540-3x=720-8x
8x-3x=720-540
5x=180
x=36
So, the measure of the angle is 36°
Related Questions
Explain how to find the value of y that would make segment OP parallel to segment LN.

Answers
Answer:
\(y = 36\)
Step-by-step explanation:
Given; the triangle above
Required
Find y
This question falls under the topic/subtopic similar triangles where we need to make comparison between similar sides'
But first, it should be noted that triangle MOP is similar to triangle MLN
This implies that
Side MP is similar to MN
Side MO is similar to ML
Mathematically; This can be represented as follows;
\(\frac{MP}{MN} = \frac{MO}{ML}\)
Where MP =y; MN = y + 18; MO = 28; ML = 28 + 14
Substitute these values in the above expression
\(\frac{y}{y+18} = \frac{28}{28+14}\)
\(\frac{y}{y+18} = \frac{28}{42}\)
Multiply both sides by 42
\(42 * \frac{y}{y+18} = \frac{28}{42} * 42\)
\(\frac{42y}{y+18} = \frac{28*42}{42}\)
\(\frac{42y}{y+18} = 28\)
Multiply both sides by y + 18
\((y+18)*\frac{42y}{y+18} = 28 * (y+18)\)
\(42y = 28 * (y+18)\)
Open Bracket
\(42y = 28 * y+28 * 18\)
\(42y = 28y+504\)
Subtract 28y from both sides
\(42y - 28y = 28y - 28y +504\)
\(14y = 504\)
Divide both sides by 14
\(\frac{14y}{14} = \frac{504}{14}\)
\(y = \frac{504}{14}\)
\(y = 36\)
Answer:
y= 36
Step-by-step explanation:
also ily, no homo
The credit remaining on a phone card (in dollars) is a linear function of the total calling time made with the card (in minutes). The remaining credit after 38 minutes of calls is 19.68, and the remaining credit after 60 minutes of calls is . What is the remaining credit after 81 minutes of calls?
Answers
Answer:
5.06
Step-by-step explanation:
Given that the remaining credit after 38 minutes of calls is 19.68, and the remaining credit after 60 minutes of calls is 12.20.
As the credit remaining on a phone card (in dollars) is a linear function of the total calling time made with the card (in minutes), so let the linear equation be
\(y=ax+b\cdots(i)\)
where y is the credit remaining on a phone card (in dollars) and x is the total calling time made with the card (in minutes).
Now, as the remaining credit after 38 minutes of calls is 19.68, so, put x=38 and y=19.68 in equation (i), we have
\(19.68=38a+b \\\\\Rightarrow b= 19.68-38a\cdots(ii)\)
Similarly, the remaining credit after 60 minutes of calls is 12.20, so, put x=60 and y=12.20 in equation (i), we have
\(12.20=60a+b \\\\\)
\(\Rightarrow 12.20=60a+(19.68-38a)\) [ by using (ii)]
\(\Rightarrow 12.20=60a+19.68-38a \\\\\Rightarrow 22a=12.20-19.68=-7.48 \\\\\Rightarrow a=-7.48/22=-0.34\)
From equation (ii),
\(b=19.68-38\times(-0.34)=32.6\)
Putting the value od a and b in equation (i), we have
\(y=-0.34x+32.6\)
So, the remaining credit after 81 minutes can be determined by putting x=81 in the above equation.
\(y=-0.34\times 81 +32.6 \\\\ \Rightarrow y=5.06\)
Hence, the remaining credit after 81 minutes of calls is $5.06.
1. Find one pair $(x,y)$ of real numbers such that $x + y = 4$ and $x^3 + y^3 = 100.$
2.For what real values of $k$ does the quadratic $12x^2 + kx + 27 = 0$ have nonreal roots? Enter your answer as an interval.
3.Find all pairs $(x,y)$ of real numbers such that $x + y = 10$ and $x^2 + y^2 = 56$.
4.Simplify $\displaystyle\frac{1-i}{2+3i}$, where $i^2 = -1.$
5.What is the smallest value of $x$ that satisfies the equation $8x^2 - 38x + 35 = 0$? Express your answer as a decimal.
Answers
1) The pairs \((x, y) = (2 + \sqrt{7}, 2 - \sqrt{7})\) and \((x, y) = (2 - \sqrt{7}, 2 + \sqrt{7})\) are solutions of the system.
2) The quadratic formula has conjugated complex roots for \(k \in (-36, 36)\).
3) The pairs \((x, y) = (5 + \sqrt{47}, 5 - \sqrt{47})\) and \((x, y) = (5 - \sqrt{47}, 5 + \sqrt{47})\) are solutions of the system.
4) The complex number \(z = \frac{1-i}{2+3\cdot i}\) is equal to the complex number \(-\frac{1}{13}-\frac{5}{13}\cdot i\).
5) \(1.25\) is the smallest value that satisfies the quadratic equation \(8\cdot x^{2}-38\cdot x + 35 = 0\).
Procedure - Miscellaneous on quadratic functions and complex numbers1) Pair of real numbers within a system of equations (I)We need to solve the following system of equations to determine at least one pair of real numbers that are its solution:
\(x+y = 4\) (1)
\(x^{3} + y^{3} = 100\) (2)
By (1) in (2) we have the following expression.
\((4-y)^{3} + y^{3} = 100\)
\(y^{2}-48\cdot y -36 = 0\) (3)
Whose solutions are: \(y_{1} = 2 + \sqrt{7}\), \(y_{2} = 2 - \sqrt{7}\)
And by (1) we find the respective solutions for \(x\): \(x_{1} = 2-\sqrt{7}\), \(x_{2} = 2 +\sqrt{7}\).
In a nutshell, the pairs \((x, y) = (2 + \sqrt{7}, 2 - \sqrt{7})\) and \((x, y) = (2 - \sqrt{7}, 2 + \sqrt{7})\) are solutions of the system. \(\blacksquare\)
2) Real values associated to conjugated complex roots of a quadratic formulaBy the Quadratic Formula we understand that roots of
\(12\cdot x^{2}+k\cdot x + 27 = 0\) are conjugated complex if and only if the following condition is observed:
\(d^{2} = k^{2}-1296 < 0\) (4)
Where \(d\) is the discriminant of the quadratic formula.
After some mathematical handling we have the following result:
\(k^{2} < 1296\)
\(-36 < k < 36\)
Hence, the quadratic formula has conjugated complex roots for \(k \in (-36, 36)\). \(\blacksquare\)
3) Pair of real numbers within a system of equations (II)By using the approach used in part 1), we find that the resulting polynomial is \(2\cdot y^{2} -20\cdot y -44 = 0\) for \(x = 10-y\), whose solutions are \((x,y) = (5 + \sqrt{47}, 5 - \sqrt{47})\) and \((x,y) = (5-\sqrt{47}, 5+\sqrt{47})\).
In a nutshell, the pairs \((x, y) = (5 + \sqrt{47}, 5 - \sqrt{47})\) and \((x, y) = (5 - \sqrt{47}, 5 + \sqrt{47})\) are solutions of the system. \(\blacksquare\)
4) Simplification of a complex numberLet be \(z = \frac{1-i}{2+3\cdot i}\), we proceed to simplify the expression by means of complex algebra:
\(\frac{1-i}{2+3\cdot i} = \frac{(1-i)\cdot (2-3\cdot i)}{(2+3\cdot i)\cdot (2-3\cdot i)} = \frac{2-5\cdot i + 3\cdot i^{2}}{2^{2}+3^{2}} = -\frac{1}{13} -\frac{5}{13} \cdot i\)
The complex number \(z = \frac{1-i}{2+3\cdot i}\) is equal to the complex number \(-\frac{1}{13}-\frac{5}{13}\cdot i\). \(\blacksquare\)
5) Determination of the least root by the quadratic formulaLet be \(8\cdot x^{2}-38\cdot x + 35 = 0\), whose roots are contained in the following quadratic formula:
\(x = \frac{38\pm \sqrt{(-38)^{2}-4\cdot (8)\cdot (35)}}{2\cdot (8)}\)
Whose solutions are: \(x_{1} = 3.5\) and \(x_{2} = 1.25\). We notice that the latter root is the smallest value of \(x\). In consequence, we conclude that \(1.25\) is the smallest value that satisfies the quadratic equation \(8\cdot x^{2}-38\cdot x + 35 = 0\). \(\blacksquare\)
RemarkThe statement is poorly formatted. Correct form is presented below:
Find one pair \((x,y)\) of real numbers such that \(x+y = 4\) and \(x^{3} + y^{3} = 100\). For what real values of \(k\) does the quadratic \(12\cdot x^{2}+k\cdot x + 27 = 0\) have nonreal roots? Enter your answer as an interval.Find all pairs \((x,y)\) of real numbers such that \(x+y = 10\) and \(x^{2}+y^{2} = 56\).Simplify \(\frac{1-i}{2+3\cdot i}\) where \(i^{2} = -1\).What is the smallest value of \(x\) that satisfies the equation \(8\cdot x^{2}-38\cdot x + 35 = 0\)? Express your answer as a decimal.To learn more on quadratic functions, we kindly invite to check this verified question: https://brainly.com/question/4119784
To learn more on complex numbers, we kindly invite to check this verified question: https://brainly.com/question/10251853
Use substitution to write an equivalent quadratic equation. (3x 2)2 7(3x 2) â€"" 8 = 0
Answers
Answer: We on da same question i do not know
Step-by-step explanation:
The function is defined by f(x)=x2e−x2 . At what values of does have a relative maximum?A ) -2B) 0C 1onlyD -1 and 1
Answers
The function f(x) = \(x^2 e^{(-x^2)}\) has a maximum value at x = 0, which is a relative maximum point.
To find the relative maximum of the function f(x) =\(x^2 e^{(-x^2)}\), we can take its first derivative, set it to zero, and solve for x.
f(x) = \(x^2 e^{(-x^2)}\)
f'(x) = \(2x e^{(-x^2)} - 2x^3 e^{(-x^2)}\)
Setting f'(x) = 0, we get:
\(2x e^{(-x^2)} - 2x^3 e^{(-x^2)} = 0\)
\(2x e^{(-x^2)} (1 - x^2) = 0\)
This equation is true when either \(2x e^{(-x^2)} = 0\) or \(1 - x^2 = 0\).
Solving \(2x e^{(-x^2)} = 0\), we get x = 0.
Solving \(1 - x^2 = 0\), we get x = 1 or x = -1.
Now, we need to determine whether these values of x correspond to relative maximum, minimum, or inflection points.
To do this, we can use the second derivative test. The second derivative of f(x) is:
f''(x) = \(2e^{(-x^2)} - 4xe^{(-x^2)} - 4x^2e^{(-x^2)}\)
At x = 0, f''(0) = 2, which is positive. This means that f(x) has a relative minimum at x = 0.
At x = 1, f''(1) = \(-6e^{(-1)}\), which is negative. This means that f(x) has a relative maximum at x = 1.
At x = -1, f''(-1) = \(-6e^{(-1)}\), which is negative. This means that f(x) has a relative maximum at x = -1.
Therefore, the answer is (D) -1 and 1 only, as these are the only values of x at which f(x) has a relative maximum.
Learn more about equation here:
https://brainly.com/question/12788590
#SPJ4
What is the measure of angle 4?
angles 1,3,5,6,7, and 8 are 73 degrees. angles 2 is 107 degrees

Answers
Answer:
34 Deg
Step-by-step explanation:
Since the Triangle is isoceles, each of the internal base angle = 180-107=73
Sum of internal angles =180, Angle4= 180-(73+73)= 180-146=34
Find Slope from 2 points (5,14) (1,6)
Answers
Answer:
8/4 or 2/1 simplified
Step-by-step explanation:
Algebraic Proof
Match the justification to each step of the deductive reasoning about this picture. Please Help!

Answers
The following are deductive reasoning for each statement in the algebraic proof given:
1. CD + DE = CE (Segment Addition Postulate)
2. 8 + (3x + 7) = 6x (Substitution)
3. 3x + 15 = 6x (Combining like terms)
4. 15 = 3x (Subtraction Property of Equality)
5. x = 5 (Division Property of Equality)
6. CE = 6(5) (Substitution)
Recall:
The Segment Addition Postulate states that when a point lies between two endpoints on a line segment, the length of the larger segment equals the sum of the lengths of the two smaller segments formed.Thus, the following are deductive reasoning for each statement in the algebraic proof given:
1. CD + DE = CE (Segment Addition Postulate)
2. 8 + (3x + 7) = 6x (Substitution)
Rationale: Plug in the values of CD, DE and CE3. 3x + 15 = 6x (Combining like terms)
Rationale: Add 8 and 7 together4. 15 = 3x (Subtraction Property of Equality)
Rationale: Subtract 3x from each side of the equation.5. x = 5 (Division Property of Equality)
Rationale: Divide each side of the equation by 3).6. CE = 6(5) (Substitution)
Rationale: Plugging in the value of x into "6x"Learn more about Segment Addition Postulate on:
https://brainly.com/question/2134445
find the slope of a line that passes through the points (-4,3) and (7,5)
Answers
Answer:
2/11
Step-by-step explanation:
5-3/7--4 = 2/11
Find the limit as (x,y) approach (0,0) of (sin(2x)-2x+y)/(x^3+y)
Answers
In this case, we cannot find the limit as (x, y) approaches (0, 0) using standard techniques. This suggests that the limit may not exist at (0, 0) for the given expression.
I'm happy to help you with your question. As (x, y) approaches (0, 0), we want to find the limit of the following expression:
(sin(2x) - 2x + y) / (x^3 + y)
To find the limit, we can use L'Hopital's Rule for the indeterminate forms 0/0 or ∞/∞. However, we first need to check if we can apply L'Hopital's Rule in this case. Since this expression involves two variables (x and y), we should attempt to rewrite the expression in terms of one variable or determine if the limit exists.
After analyzing the given expression, it is difficult to rewrite it in terms of a single variable or directly apply L'Hopital's Rule. In this case, we cannot find the limit as (x, y) approaches (0, 0) using standard techniques. This suggests that the limit may not exist at (0, 0) for the given expression.
To know more about sin(x) visit :
https://brainly.com/question/1414638
#SPJ11
Question 3 (3 points) Determine the smallest integer that makes 4x - 9 - 2x < 5x + 1 true
a 4
b 3
c 2
d 1
Answers
Answer:
d:1
Step-by-step explanation:
the answers will always be negative and the other side will always be positive
PLEASE HELP ASAP! NEED REAL ANSWERS!

Answers
The vertex of y=|2x+4|+5 is (-2, 5) and Range of the y=|2x+4|+5 is 5≤y<∞
What is a function?A relation is a function if it has only one y-value for each x-value.
We need to find the vertex and range of y=|2x+4|+5
f(x)=2x+4
f of x is equal to zero
2x+4=0
Subtract 4 from both sides
2x=-4
Divide both sides by 2
x=-2
y=|2x+4|+5
=|2(-2)+4|+5=|-4+4|+5=5
Hence vertex is (-2, 5)
The range of the y=|2x+4|+5 is 5≤y<∞
Hence vertex is (-2, 5) and Range of the y=|2x+4|+5 is 5≤y<∞
To learn more on Functions click:
https://brainly.com/question/21145944
#SPJ1
Find the slope of the line

Answers
Answer:
1/2
Step-by-step explanation:
Pick two points on the line
I picked (0, 2) and (2, 3)
m = (3-2)/(2 -0) = 1/2
(5m-7)+(6m + 9) what is the answer
Answers
Answer:
11m + 2
Step-by-step explanation:
Combine like-terms.
5m + 6m = 11m
-7 + 9 = 2
Answer:
m= 16
Step-by-step explanation:
first you would rewrite the statement
then you would subtract 5m -6m =M
then you subtract 7 from 9 =16
so your answer is M=16
can I get the brainliest?
Consider a hash table, a hash function of key % 10. Which of the following programmer-defined constants for quadratic probing cannot be used in a quadratic probing equation? O c1 = 1 and 2 = 0 O c1 = 5 and c2 = 1 O c1 = 1 and c2 - 5 O c1 = 10 and 2
Answers
D: "\(c_{1} = 10\) and \(c_{2} = 2\)" are programmer-defined constants for quadratic probing that cannot be used in a quadratic probing equation. Option D is correct answer.
The quadratic probing equation is defined as:
h (k, i) = (h′(k) + \(c_{1}\) * i + \(c_{2}\) * i^2) mod m,
where h′(k) is the hash value of key
k and m is the size of the hash table.
The constants \(c_{1}\) and \(c_{2}\) are programmer-defined constants that are used to compute the new hash index when a collision occurs in the hash table.
The given hash function is h(k) = k % 10.
Therefore, the hash value of any key will be between `0` and `9`.Now, let's check which of the given programmer-defined constants for quadratic probing cannot be used in a quadratic probing equation:
Option A: `c1 = 1 and c2 = 0`This option can be used in the quadratic probing equation. It means that linear probing is being used.
Option B: \(c_1 = 5\) and \(c_2 = 1\) This option can be used in the quadratic probing equation. It means that the new index is being computed as `h(k, i) = (h′(k) + 5i + i^2) mod m`.
Option C: \(c_1 = 1\) and \(c_2 = 5\) This option can be used in the quadratic probing equation. It means that the new index is being computed as `h(k, i) = (h′(k) + i + 5i^2) mod m`.
Option D: \(c_1 = 10\) and \(c_2 = 2\) This option cannot be used in the quadratic probing equation. It means that the new index is being computed as `h(k, i) = (h′(k) + 10i + 2i^2) mod m`.
Since \(c_{1}\) is greater than or equal to `m`, this equation will always result in a hash index that is greater than or equal to `m`. Therefore, it is not possible to use `\(c_{1}\)= 10` in the quadratic probing equation. Hence, the correct option is D.
You can learn more about quadratic probing equation at
https://brainly.com/question/30033698
#SPJ11
Error Analysis A garderer plans to extend the length of a rectangular garden by 4 feet. Let x
represent the garden's original length. The expression 8(x + 4) represents the area of the garden,
where 8 is the width, in feet, and (x + 4) represents the extended length, in feet, of the garden.
When asked for the area of the extended portion, the gardener incorrectly said it was 12 square
feet. Expand the expression to find the area of the extension. Then describe an error the gardener
might have made.
Answers
The correct Area of extended portion will be 28 square feet
A rectangle in the Euclidean plane is a quadrilateral with four right angles. Other names for it include a parallelogram with a right angle and an equiangular quadrilateral, where equiangular means that all of its angles are equal. Four equally long sides make to a square, which is a rectangle.
Area of original garden=length*breadth=4 × x=4x square feet
Area of extended garden=4 × 7=28 sq. feet
Total area (including the extended portion)=4x+28=
4(x+7) square feet
The mistake made by gardener is that he added 4+7=11 square feet
But correct area of extended portion= length*breadth=4 × 7=28 square feet.
Learn more about Area:
brainly.com/question/11952845
#SPJ4
unit 6 homework 3
help please

Answers
Part 1: Triangles are similar by Side-Side-Side similarity.
Part 2: Triangles are similar angle-Angle (AA) similarity.
Explain about the similarity of the triangles?The 3 triangle similarity theorems, Side-Angle-Side (SAS), Angle-Angle (AA), and Side-Side-Side (SSS), can also be used to compare two triangles.Triangles are similar if they have two that share a single angle type, or AA (Angle-Angle). Triangles are identical if they have two sets of proportional sides with equal included angles, or SAS (Side-Angle-Side).Part 1: Ratios must be equal for triangle similarity.
Taking the ratios of the sides:
17/37.4 = 20/44 = 25/55
On solving
0.4545 = 0.4545 = 0.4545
As the ratios are equal, triangles are similar.by Side-Side-Side similarity.
Part 2:
∠F = ∠H (given)
∠EGF = ∠JGH (vertically opposite)
By Angle-Angle (AA) similarity.
Know more about the similarity of the triangles
https://brainly.com/question/14285697
#SPJ1
The correct question is 1 and 2.
What is the vertex of f(x) = 3|x|
Answers
Answer:
\(3 \times |x| = 0 \\ 3 \times |x| \div 3 = 0 \div 3 \\ |x | = 0 \\ x = 0\)
Sine is positive in which of the following quadrants?
A. I and III
B. I and IV
C. T and II
D. II and III
Answers
Answer:
C. I and II
Step-by-step explanation:
In q1, all trig functions are positive. q2, sin and csc is positve. hope this helps!!
Question 1miles.126,720 inches are equal toO a. 10,560O b. 1.3O c. 2O d. 24

Answers
The question gives,
\(126,720\text{ inches}\)We would start by converting this into feet. The conversion rate is
\(12\text{inches}=1\text{foot}\)Therefore, the conversion would be;
\(\begin{gathered} 12\text{inches}=1\text{foot} \\ 126720\text{inches}=\frac{126720}{12}\text{feet} \\ 126720in=10560ft \end{gathered}\)Also, to convert feet into miles, the conversion rate is;
\(\begin{gathered} 5280ft=1mile \\ \text{Therefore;} \\ 10560ft=\frac{10560}{5280}\text{miles} \\ 10560ft=2miles \end{gathered}\)ANSWER:
The correct answer is option C: 2 miles
-2c + 3c - 5 - 4c + 7
Answers
Answer:−
3c+2
Step-by-step explanation:
Answer:
−3c +2
Step-by-step explanation:
Combine Like Terms
when constructing a confidence interval for the mean of a distribution based on one sample, how is confidence level determined?
Answers
Constructing a confidence interval for the mean of a distribution based on one sample is Confidence level = 1 - significance level.
The definition of the confidence level is (1-α). Zα is the number of standard deviations from the mean at which X with a certain probability lies. If Z = 1.96 is selected, the likelihood that the real mean falls inside the range is set at 0.95, hence we are asking for the 95% confidence interval.
Let us consider,
Confidence level = c
significance level \(= \alpha\)
\(c = 1 - \alpha\)
Fore more such question on confidence level.
https://brainly.com/question/29634773
#SPJ4
You are dealt one card from a standard 52-card deck. Find the probability of being dealt a spade.
The probability of being dealt a spade is
Answers
Answer:
The probability of being dealt a spade is 13/52.
Step-by-step explanation:
Consider the graph of function g
y4
If f(x)=x², which equation represents function g?
OA. g(z) f(27)
OB. g (2) f(42)
M
2
O C. g(z) = 2 f(z)
(2)
D. 9(2) -
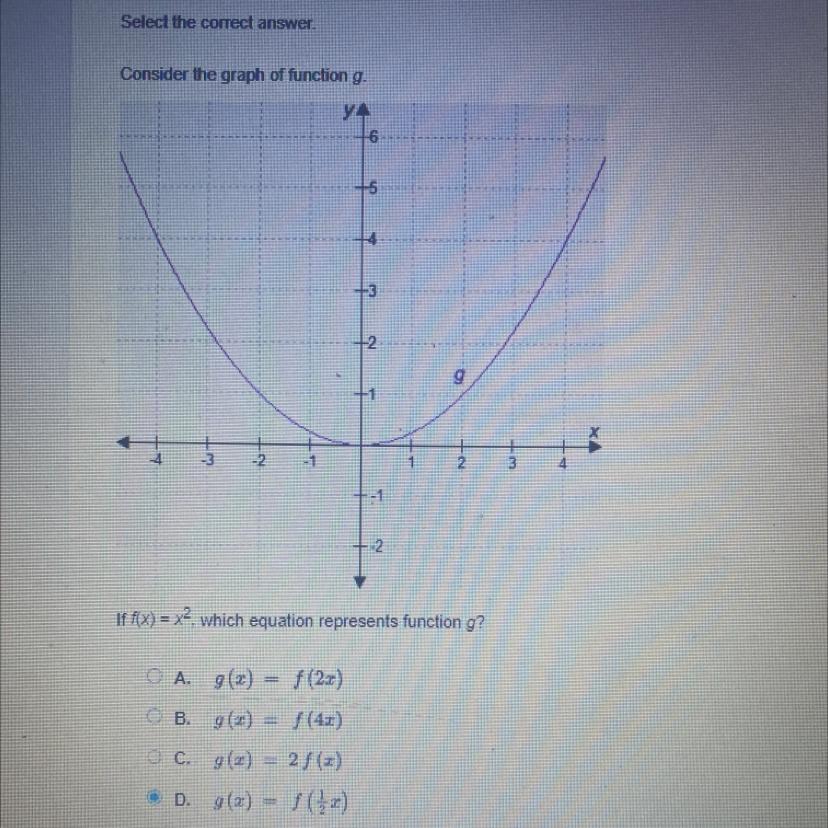
Answers
Answer:
D
Step-by-step explanation:
A baseball "diamond" actually forms a square, each side measuring 30 yards. How far, to the nearest yard, must the third baseman throw the ball to reach first base?
Answers
Answer:
15 yards
Step-by-step explanation:
the pitcher is in the middle of the diamond square thingy,the length is 30, so half of 30 is 15
a spinner with four equal sections labeled 1-4 is spun four times. What is the probability that at least 2 of the spins result in a 1?
Answers
The probability of getting at least 2 1's in 4 spins is:
1 - 0.7383 = 0.2617 or approximately 26.17%.
What is probability?Probability is a way to gauge how likely something is to happen. Many things are difficult to forecast with absolute confidence. Using it, we can only make predictions about the likelihood of an event happening, or how likely it is.
To calculate the probability that at least 2 of the spins result in a 1, we can use the complement rule and subtract the probability that fewer than 2 of the spins result in a 1 from 1.
The probability of getting exactly 0 1's in 4 spins is:
(3/4)⁴ = 0.3164
The probability of getting exactly 1 1 in 4 spins is:
4 * (1/4) * (3/4)³ = 0.4219
So the probability of getting 0 or 1 1's in 4 spins is:
0.3164 + 0.4219 = 0.7383
Therefore, the probability of getting at least 2 1's in 4 spins is:
1 - 0.7383 = 0.2617 or approximately 26.17%.
Learn more about probability on:
https://brainly.com/question/13604758
#SPJ1
Mitch ran 5/2 of a mile in 1/3 of an hour. How many hours will it take Mitch to run 1 mile?
Answers
It will take 15/2 hours for Mitch to run 1 mile. Cancelling out the common factors from numerator and denominator, the ratio reduces to 15/2.
Mitch ran 5/2 of a mile in 1/3 of an hour. To calculate how many hours it will take Mitch to run 1 mile, we need to use a ratio. The ratio is (5/2)/(1/3). To solve this, we need to multiply the numerator and denominator of the first fraction with the denominator of the second fraction, and then multiply the numerator and denominator of the second fraction with the denominator of the first fraction. So, the ratio becomes (5/2)*(3/1)/(1/3)*(2/1). Cancelling out the common factors from numerator and denominator, the ratio reduces to 15/2. This means that it will take 15/2 hours for Mitch to run 1 mile.
Learn more about hours here:
https://brainly.com/question/20379233
#SPJ4
For events A, B, and C we have that
P(A)=0.24,
P(B)=0.26,
P(A n B)=0.05,
P(A n C)=0.05,
P(B n C)=0.05,
P(A n B n C)=0.02 and P((A u B uC)^/)=0.33,
find P(C)
How should i go about this??
Answers
=================================================
Work Shown:
P( (A u B u C)' ) = 0.33
P(A u B u C) = 1 - P( (A u B u C)' )
P(A u B u C) = 1 - 0.33
P(A u B u C) = 0.67
--------
P(AuBuC) = P(A)+P(B)+P(C)-P(AnB)-P(AnC)-P(BnC)+P(AnBnC)
0.67 = 0.24 + 0.26 + P(C) - 0.05 - 0.05 - 0.05 + 0.02
0.67 = P(C) + 0.37
P(C) = 0.67 - 0.37
P(C) = 0.30
For more information, search out "inclusion-exclusion principle". Also feel free to ask me if you have any questions.
X= _______
and y= ________

Answers
Answer:
z comes after y in the alphabet
You are considering investing in a security that will pay you $3,000 in 34 years. a. If the appropriate discount rate is 8 percent, what is the present value of this investment? b. Assume these investments sell for $773 in return for which you receive $3,000 in 34 years. What is the rate of return investors earn on this investment if they buy it for $773? a. If the appropriate discount rate is 8 percent, the present value of this investment is $ 219.13. (Round to the nearest cent.) b. The rate of return investors can earn on this investment if they buy it for $773 is %. (Round to two decimal places.)
Answers
In this scenario, we are considering an investment that will pay $3,000 in 34 years. We are given an appropriate discount rate of 8 percent. To determine the present value of this investment, we can use the present value formula. Additionally, we are provided with the information that the investment is being sold for $773, and we need to calculate the rate of return investors will earn on this investment.
a. Present value of the investment:
To calculate the present value of the investment, we use the present value formula:
Present Value = Future Value / (1 + Discount Rate)^n,
where Future Value is $3,000, the Discount Rate is 8 percent (0.08), and n is the number of years, which is 34 in this case.
Present Value = $3,000 / (1 + 0.08)^34 = $219.13
Therefore, the present value of the investment, considering an 8 percent discount rate, is $219.13.
b. Rate of return on the investment:
The rate of return on an investment is calculated using the formula:
Rate of Return = (Future Value - Purchase Price) / Purchase Price * 100,
where Future Value is $3,000 and the Purchase Price is $773.
Rate of Return = ($3,000 - $773) / $773 * 100 ≈ 288.46%
Therefore, the rate of return investors can earn on this investment, if they buy it for $773, is approximately 288.46%.
Learn more about percent here:
https://brainly.com/question/31323953
#SPJ11