#1Write each of the following as a rational number.a. 11b. 3student work?C.-4
Answers
Rational numbers are numbers that can be expressed as quatients or fractions of two integers, with a numerator, p, and a denominator, q. The denominator of the fraction is always greater than zero.
Since q can be 1, you can think of every integer as a rational number.
a) 11
\(\frac{11}{1}\)By dividing 11 by 1, you express the integer as a rational number.
b) 3
\(\frac{3}{1}\)c) -4
Same as in a and b you can divide it by 1 to express it as a rational number
\(-\frac{4}{1}\)Since -4 is not a prime number like 11 and 3 you can also write it as:
\(-\frac{8}{2}\)Related Questions
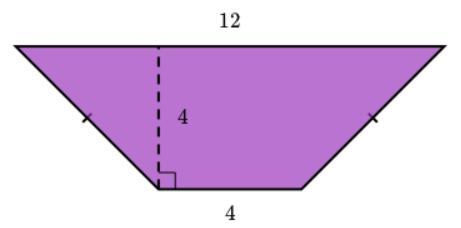
Find the area of the shape shown below.
Answers
Answer:
The answer is 32
Step-by-step explanation:
The formula for finding the area of a trapezoid is:
((base 1 + base 2)/ 2 )* h
Now all you have to do is substitute the numbers in.
Note: bases will always be the ones like 12 and 4 in this case. We have just named then 1 and 2.
Answer:
32 square units
Step-by-step explanation:
\(\displaystyle A=\frac{1}{2}(b_1+b_2)h=\frac{1}{2}(12+4)(4)=\frac{1}{2}(16)(4)=\frac{1}{2}(64)=32\)
Note that \(b_1\) and \(b_2\) are the lengths of each base of the trapezoid, so it doesn't matter which is which.
The distribution of lifetimes of a particular brand of car tires has a mean of 51,200 miles and a standard deviation of 8,200 miles. Assuming that the distribution of lifetimes is approximately normally distributed and rounding your answers to the nearest thousandth, find the probability that a randomly selected tire lasts: A) Between 55,000 and 65,000 miles B) Less than 48,000 miles C) At least 41,000 miles D) A lifetime that is within 10,000 miles of the mean
Answers
Answer:
a) 0.277 = 27.7% probability that a randomly selected tyre lasts between 55,000 and 65,000 miles.
b) 0.348 = 34.8% probability that a randomly selected tyre lasts less than 48,000 miles.
c) 0.892 = 89.2% probability that a randomly selected tyre lasts at least 41,000 miles.
d) 0.778 = 77.8% probability that a randomly selected tyre has a lifetime that is within 10,000 miles of the mean
Step-by-step explanation:
Problems of normally distributed distributions are solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this question, we have that:
\(\mu = 51200, \sigma = 8200\)
Probabilities:
A) Between 55,000 and 65,000 miles
This is the pvalue of Z when X = 65000 subtracted by the pvalue of Z when X = 55000. So
X = 65000
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{65000 - 51200}{8200}\)
\(Z = 1.68\)
\(Z = 1.68\) has a pvalue of 0.954
X = 55000
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{55000 - 51200}{8200}\)
\(Z = 0.46\)
\(Z = 0.46\) has a pvalue of 0.677
0.954 - 0.677 = 0.277
0.277 = 27.7% probability that a randomly selected tyre lasts between 55,000 and 65,000 miles.
B) Less than 48,000 miles
This is the pvalue of Z when X = 48000. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{48000 - 51200}{8200}\)
\(Z = -0.39\)
\(Z = -0.39\) has a pvalue of 0.348
0.348 = 34.8% probability that a randomly selected tyre lasts less than 48,000 miles.
C) At least 41,000 miles
This is 1 subtracted by the pvalue of Z when X = 41,000. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{41000 - 51200}{8200}\)
\(Z = -1.24\)
\(Z = -1.24\) has a pvalue of 0.108
1 - 0.108 = 0.892
0.892 = 89.2% probability that a randomly selected tyre lasts at least 41,000 miles.
D) A lifetime that is within 10,000 miles of the mean
This is the pvalue of Z when X = 51200 + 10000 = 61200 subtracted by the pvalue of Z when X = 51200 - 10000 = 412000. So
X = 61200
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{61200 - 51200}{8200}\)
\(Z = 1.22\)
\(Z = 1.22\) has a pvalue of 0.889
X = 41200
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{41200 - 51200}{8200}\)
\(Z = -1.22\)
\(Z = -1.22\) has a pvalue of 0.111
0.889 - 0.111 = 0.778
0.778 = 77.8% probability that a randomly selected tyre has a lifetime that is within 10,000 miles of the mean
X
A cylinder has a circular base with a diameter of 12 ft. The height of the cylinder is 4 ft. What is the volume of the cylinder rounded to the nearest whole
number? Use 3.14 for p
A. 45267
B. 1.809 €
C. 1516
D 6036
vered
Answers
Explanation: credits to her
Pls answer this fast

Answers
Answer: C
Step-by-step explanation:
1. divide 3 by 2 to find out how many pounds of blueberries she picked each day. 3/2 is 1.5
2. multiply 1.5 by 16 to convert to ounces. 1.5x16 is 24.
3. she picked 24 ounces of blueberries each day.
Suppose the prices of a certain model of new homes are normally distributed with a mean of 150,000. Use the 68-95-99.7 rule to find the percentage of buyers who paid between $149,000 and $151,000 if the standard deviation is $1000
Answers
The percentage of buyers is approximately 68.26% of buyers of new houses paid between \($149,000\) and \($151,000\) .
We are given that the prices of the new homes are normally distributed with a mean of \($150,000\) and a standard deviation of $1000.
Using the 68-95-99.7 rule, we know that: approximately 68% of the data falls within one standard deviation of the mean approximately 95% of the data falls within two standard deviations of the mean, approximately 99.7% of the data falls within three standard deviations of the mean.
In order to determine the proportion of customers who spent between $149,000 and , we must first determine the z-scores for these values:
z1 = (149,000 - 150,000) / 1000 = -1 z2 = (151,000 - 150,000) / 1000 = 1
Now, we can determine the proportion of data that falls between z1 and z2 using the z-table or a calculator. The region to the left of z1 is 0.1587, and the area to the left of z2 is 0.8413, according to the z-table. Thus, the region bounded by z1 and z2 is:
0.8413 - 0.1587 = 0.6826
We can get the percentage of consumers who spent between by multiplying this by 100% is \($149,000\) and \($151,000\):
0.6826 x 100% = 68.26%
Therefore, the standard deviation of customers who paid between is \($149,000\) and \($151,000\) for this model of new homes.
For such more questions on standard deviation
https://brainly.com/question/30557671
#SPJ11
The equation p(t) = 1.e represents a
population of bacteria, in thousands, 1 days
after it was first counted. Here is a graph of
y = p(t).
Select all the true statements.
Answers
Answer:
(b), (d) and (e)
Step-by-step explanation:
Given
\(p(t) = 1 * e^t\)
See attachment for \(y = p(t)\)
Required
Select true statements from the given options
(a) \(\ln(30)\) = days the bacteria reaches 30000
We have:
\(p(t) = 1 * e^t\)
In this case:
\(t = \ln(30)\) and \(p(t) = 30000\)
So, we have:
\(30000 = 1 * e^{\ln(30)}\)
\(30000 = e^{\ln(30)}\)
Using a calculator, we have:
\(e^{\ln(30)} = 30\)
So:
\(30000 = 30\)
The above equation is false.
(a) is not true
(b) The graph shows that \(\ln(20) \approx 3\)
We have:
\(p(t) = 1 * e^t\)
Let t = 3
So;
\(p(3) = 1 * e^3\)
From the graph, \(p(3) = 20\)
So:
\(20 = 1 * e^3\)
\(20 = e^3\)
Take natural logarithm of both sides
\(\ln(20) = \ln(e^3)\)
This gives:
\(\ln(20) = 3\)
(b) is true
(c) \(\ln(t) = y\) is the logarithm form of \(y = e^t\)
We have:
\(y = e^t\)
Take natural logarithm of both sides
\(\ln(y) = \ln(e^t)\)
This gives:
\(\ln(y) = t\)
\(\ln(y) = t\) \(\ne\) \(\ln(t) = y\)
(c) is false
(d) \(e^4 > 50\) and \(\ln(50) < 4\)
From the graph, we have:
\(e^4 = 54\) --- rough readings
This implies that:
\(e^4 > 50\) is true
Because \(54 > 50\)
Take natural logarithm of both sides
\(\ln(54) > \ln(50)\)
Rewrite as:
\(\ln(50) < \ln(54)\)
We have:
\(e^4 = 54\)
Take natural logarithm of both sides
\(\ln(e^4) = \ln(54)\)
\(4 = \ln(54)\)
\(\ln(54) = 4\)
Substitute \(\ln(54) = 4\) in \(\ln(50) < \ln(54)\)
\(\ln(50) < 4\)
(d) is true
(e) The graph shows that \(10 \approx \ln(2.3)\)
We have:
\(p(t) = 1 * e^t\)
Let t = 2.3
So;
\(p(2.3) = 1 * e^{2.3}\)
From the graph,
\(p(2.3) = 10\) ---- rough readings
So:
\(10 = 1 * e^{2.3}\)
\(10 = e^{2.3}\)
Take natural logarithm of both sides
\(\ln(10) = \ln(e^{2.3})\)
This gives:
\(\ln(10) = 2.3\)
(e) is true

PLZ HELP FIND THE PERIMETER

Answers
Answer:
254 ft
Step-by-step explanation:
first find the legs of the triangle.
you already know 65, and you would get another leg by 83-50, which equals 33.
Next use pythagorean theorem to find the other leg
a^2+b^2=c^2
rearrange so you find a leg
a^2=c^2-b^2
a^2=65^2-33^2
a^2=4225-1089
a^2=3136
a=56
Now you know that the missing leg is 56. Since that leg is the same as the short side of the rectangle, you 83+50+65+56=254
In circle N with � ∠ � � � = 12 4 ∘ m∠MNP=124 ∘ and � � = 13 MN=13, find the area of sector MNP. Round to the nearest hundredth.
Answers
If circle with center N with m∠MNP=124 ∘ and MN=13, the area of sector MNP is approximately equal to 194.86 square units.
To find the area of a sector of a circle, we need to use the formula:
Area of sector = (central angle/360°) x πr²
Where r is the radius of the circle.
In this problem, we know that the central angle m∠MNP is 124° and MN, which is also the radius of the circle, is 13. So we can substitute these values into the formula:
Area of sector = (124/360) x π(13)²
Area of sector ≈ 194.86
Therefore, the area of sector MNP is approximately equal to 194.86 square units.
To learn more about sector click on,
https://brainly.com/question/23857683
#SPJ1
two questions please just one needs to be correct either one i'm not picky i just really need help


Answers
Answer:
Your math problem isnt showing up
integrate both sides of the differential equation you found for dp to obtain an equation for p . your equation should then include a constant that depends on initial conditions. determine the value of this constant by assuming that the pressure at some reference height y0 is p0 .
Answers
The value of this constant, by assuming that the pressure at some reference height y₀ is p₀, is p - p₀ = p.g(y₀ - y).
dp = -pg dy
At height y = y₀ and p = p₀
∫dp = ∫-pg dy
⇒p = -pgy + C Eqn(1)
Where c is the constant of integration
We know that y = y₀ and p = p₀
⇒p₀ = -pgy₀ + C
⇒C = p₀ + pgy₀
Put the value of C in Eqn(1)
⇒p = -pgy + p₀ + pgy₀
⇒p - p₀ = -pgy + pgy₀
⇒p - p₀ = pg(y₀ - y)
To know more about pressure, here
https://brainly.com/question/30244346
#SPJ4

HELP ASAP PLSS! The graph represents the relationship between the amount of money a babysitter makes, m, and the hours the baby sitter works, h. Which function can be used to determine the amount of money the babysitter makes, d, after h hours? d=17h+5 d = 5h + 7 d = 7h +5 d=15h+7
Answers
Answer:
d = 7h +5
Step-by-step explanation
If you go to K-12 then this is the right answer I just took the quiz.
Answer:
d = 7h +5

A candy distributor needs to mix a 10% fat-content chocolate with a 60% fat-content chocolate to create
100 kilograms of a 25% fat-content chocolate. How many kilograms of each kind of chocolate must they
use?
Answer: They must mix
Kilograms of the 10% chocolate and
Kilograms of the 60% chocolate.
Answers
Answer:
They must mix 70 kilograms of the 10% chocolate and 30 kilograms of the 60% chocolate.
Step-by-step explanation:
Given that a candy distributor needs to mix a 10% fat-content chocolate with a 60% fat-content chocolate to create 100 kilograms of a 25% fat-content chocolate, to determine how many kilograms of each kind of chocolate must they use, the following calculations must be performed:
10 x 0.5 + 60 x 0.5 = 35
10 x 0.6 + 60 x 0.4 = 30
10 x 0.7 + 60 x 0.3 = 25
100 x 0.7 = 70
Thus, they must mix 70 kilograms of the 10% chocolate and 30 kilograms of the 60% chocolate.
What is the multiplicative rate of change between 10,50 and 250
Answers
Answer:D
Step-by-step explanation:
An isosceles triangle has a vertex angle of 70°. What is the measure of each base angle?
70°
55°
20°
Answers
Answer: 55 degrees (choice B)
============================================================
Explanation:
Let x be the measure of each congruent base angle.
The three interior angles of any triangle always add to 180 degrees.
x+x+70 = 180
2x+70 = 180
2x = 180-70
2x = 110
x = 110/2
x = 55 degrees
Answer:
55 degrees
Step-by-step explanation:
Since the triangle is isosceles there are two congruent base angles and 1 vertex angle. The three angles add up to 180 degrees.
180 minus the vertex angle of 70 degrees leaves 110 degrees for the remaining two angles. Divide 110 by 2 to get the measure of each base angle.
180 - 70 = 110/2 = 55 degrees
Which term of the sequence 1/4;-1;-21/4;...is equal to -131/2
Answers
11, - 6, -1, 4, 9, 14, 19, ... are mapped onto 4. ... A;-l = (-ltQn (mod N),. (A5.34) ... 131 2, 14, 34, 38, 42, 78, 90, 178, 778, 974(1000).
Step-by-step explanation:
the nearest .1/2 incp, we say the 'unit 131/2 incl. 1.4 a measUrement is-stated tp- be 546 inch, this UM= the
make e the subject
e-5=2f
Answers
Answer:
e-5=2f
take '-5' to the other side where '2f' is
e=2f+5
Which has a greater effect on the volume-changing the radius by a given amount or changing the height by the same amount? Why?
Answers
Answer: Changing the radius of an object by a given amount has a greater effect on the volume than changing the height by the same amount. The volume of a cylinder is given by the formula V = πr²h, where V is the volume, r is the radius, and h is the height. If we change the radius by a given amount, say x, the new radius would be r+x. Hence, the new volume would be V' = π(r+x)²h = π(r²+2rx+x²)h = V + 2πrxh + πx²h. We can see that the volume change equals 2πrxh + πx²h. The first term is proportional to both the radius and the height, whereas the second term is proportional to the square of the radius and the height. Assuming that the height change is also x, the new volume would be V'' = πr²(h+x) = V + πr²x. We can see that the volume change is proportional to the radius squared and the change in height. Therefore, changing the radius by a given amount has a greater effect on the volume than changing the height by the same amount.
Christine drives her car 144 miles and has an average of a certain speed. If the average speed has been 5 mph more, she could have traveled 168 miles in the same length of time. What was her average speed?
Answers
Let's make a system of equations:
144/x=y
168/(x+5)=y
So,
144/x=168/(x+5)
Solving using cross multiplication,
x=30
So, her average speed for driving 144 miles was 30 miles per hour.
-Hunter
factor and solve
x^2-4x=5
Answers
Let’s solve the equation x^2 - 4x = 5 by factoring:
First, we’ll move all the terms to one side of the equation:
x^2 - 4x - 5 = 0
Now, we’ll factor the left side of the equation. We’re looking for two numbers that multiply to -5 and add to -4. Those numbers are -5 and 1. So we can write:
(x - 5) (x + 1) = 0
Now we’ll use the zero-product property to solve for x. This property states that if the product of two numbers is zero, then at least one of the numbers must be zero. So we have:
x - 5 = 0 or x + 1 = 0
Solving each equation separately, we find that x = 5 or x = -1.
So, the solutions to the equation x^2 - 4x = 5 are x = 5 and x = -1.
In a lottery game, a single ball is drawn at random from a container that contains 25 identical balls numbered from 1 through 25. Use the equation P(AUB)=P(A) + P(B) - P(ANB), where A and B are any events, to compute the probability that the number drawn is prime or greater than 12.
The probability that the number drawn is prime or greater than 12 is : ___________
Answers
Answer:
17/25
Step-by-step explanation:
The equation for the probability of two events that are not mutually exclusive is:
p(A ∨ B) = p(A) + p(B) - p(A ∧ B)
A = the number is prime
B = the number is prime
The numbers are:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25
Here are the 8 prime numbers that satisfy event A:
3, 5, 7, 11, 13, 17, 19, 23
p(A) = 8/25
Here are the 13 numbers that are greater than 12 that satisfy event B:
13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25
p(B) = 13/25
Here are the 4 numbers that satisfy both event A and event B:
13, 17, 19, 23
p(A ∧ B) = 4/25
p(A ∨ B) = p(A) + p(B) - p(A ∧ B)
p(A ∨ B) = 8/25 + 13/25 - 4/25
p(A ∨ B) = 17/25
The probability that the number drawn is prime or greater than 12 = \(\frac{18}{25}\)
What is probability?"Probability is a branch of mathematics which deals with finding out the likelihood of the occurrence of an event."
Formula of the probability of an event A is:P(A) = n(A)/n(S)
where, n(A) is the number of favorable outcomes, n(S) is the total number of events in the sample space.
For given question,
In a lottery game, a single ball is drawn at random from a container that contains 25 identical balls numbered from 1 through 25.
n(S) = 25
Let event A: the number drawn is prime
The prime numbers from 1 to 25 are:
2, 3, 5, 7, 11, 13, 17, 19, 23
So, n(A) = 9
The probability that the number drawn is prime,
\(P(A)=\frac{n(A)}{n(S)}\\\\ P(A)=\frac{9}{25}\)
Let event B: the number drawn is greater than 12
So, n(B) = 13
The probability that the number drawn is greater than 12,
\(P(B)=\frac{n(B)}{n(S)}\\\\ P(B)=\frac{13}{25}\)
The number drawn is prime as well as greater than 12.
Such numbers are : 13, 17, 19, 23
n(A ∩ B) = 4
So, the probability that the number drawn is prime as well as greater than 12,
\(P(A\cap B)=\frac{n(A\cap B)}{n(s)}\\\\ P(A\cap B)=\frac{4}{25}\)
Using the equation P(AUB) = P(A) + P(B) - P(A ∩ B) to find the probability that the number drawn is prime or greater than 12,
\(\Rightarrow P(A\cup B)=P(A)+P(B)-P(A\cap B)\\\\\Rightarrow P(A\cup B)=\frac{9}{25}+ \frac{13}{25} -\frac{4}{25} \\\\\Rightarrow P(A\cup B)=\frac{9+13-4}{25}\\\\ \Rightarrow P(A\cup B)=\frac{18}{25}\)
Therefore, the probability that the number drawn is prime or greater than 12 = \(\frac{18}{25}\)
Learn more about probability here:
brainly.com/question/11234923
#SPJ2
SOMEONE PLEASE HELP ME!!!
What are the x-intercepts of the graph of the function y=6tan(x/2)-3?
Answers
Step-by-step explanation:
\(y = 6 \tan( \frac{x}{2} ) - 3\)
Set y=0
\(0 = 6 \tan( \frac{x}{2} ) - 3\)
\(3 = 6 \tan( \frac{x}{2} ) \)
\( \frac{1}{2} = \tan( \frac{x}{2} ) \)
\( \tan {}^{ - 1} ( \frac{1}{2} ) + \pi = \frac{x}{2} \)
Multiply both sides by 2
\(2 \tan {}^{ - 1} ( \frac{1}{2} ) + 2\pi = x\)
So the x intercepts of the function is
\(2 \tan {}^{ - 1} ( \frac{1}{2} ) + 2\pi\)n
A radioactive compound with mass 260 grams decays at a rate of 3.8% per hour. Which equation represents how many grams of the compound will remain after 8 hours?
Answers
Approximately 138.3 grams of the compound will remain after 8 hours. The decay of a radioactive compound is an exponential process, which can be modeled by the equation:
N(t) = N₀ * e^(-λt)
where N(t) is the amount of the compound remaining at time t, N₀ is the initial amount of the compound, λ is the decay constant, and e is the mathematical constant known as Euler's number.
To find the amount of the compound remaining after 8 hours, we need to plug in the given values into the equation above. We know that the initial mass of the compound is 260 grams, and the decay rate is 3.8% per hour, which means that the decay constant λ is equal to 0.038. Therefore, the equation becomes:
N(8) = 260 * e^(-0.038 * 8)
Simplifying this equation gives:
N(8) = 260 * e^(-0.304)
N(8) ≈ 138.3 grams
Therefore, approximately 138.3 grams of the compound will remain after 8 hours.
It's important to note that this calculation assumes that the decay rate remains constant over time, which may not always be the case in reality. Additionally, the actual amount of the compound remaining may vary due to experimental error or other factors.
Learn more about Euler's number here:
https://brainly.com/question/30639766
#SPJ1
After completing your analysis of the rating system, you determine that any rating greater than or equal to 3.5 points can be considered a high rating. You also know that Chocolate and Tea considers a bar to be super dark chocolate if the bar's cocoa percent is greater than or equal to 70%. You decide to create a new data frame to find out which chocolate bars meet these two conditions.
Assume the first part of your code is:
best_trimmed_flavors_df <- trimmed_flavors_df %>%
You want to apply the filter() function to the variables Cocoa.Percent and Rating. Add the code chunk that lets you filter the data frame for chocolate bars that contain at least 70% cocoa and have a rating of at least 3.5 points.
What rating appears in row 1 of your tibble?
0 / 1 point
3.75
3.50
4.25
4.00
Answers
As a result, option two (3.50) is correct.
Step-by-step explanation:
The code chunk that allows you to filter the data frame for chocolate bars with at least 70% cocoa and a rating of at least 3.5 pounds is as follows
∴ filter(Cocoa, percent>='70%'&Rating>=3.5)
Therefore, the code you write is facet wrap(Cocoa. Percent). Facet wrap() is a function in this code chunk that allows you to wrap a variable's facets. All of the ingredients are derived from cocoa beans. Cacao solids (the "brown" part, which contains health benefits and the unmistakable chocolatey flavor) and cacao butter (the "white" part, which contains the chocolate's fatty component) are split in proportion.
As a result, 3.5 appears in row 1 of your Tibble.
Other options I (iii), and (iv) are incorrect because the question states that any rating greater than or equal to 3.5 points can be considered a
high rating, and the rating here should be 3.5, not 3.75, 4.25, or 4
So, option (ii) is correct.
To learn more about Rating of cocoa butter
https://brainly.com/question/2972328
#SPJ4
In the following figure, OQ and OR are internal bisectors of ZQ
and ZR, respectively, then prove that ZQOR = 90° +- ZP.
1
2
Р
R.
Answers
Answer:
if you can provide the figure it would be quite easy for the people giving answers
It is very important that you
and avoid errors to happen.
Review
Instruction:
Factor each of the following quadratic expression.
1. x² + x
2. 5x2 - 25x
3. x2 - 16
4. x² + 4x + 4
5. x2 - 5x + 6
Answers
Step-by-step explanation:
Given expressions:
1. x² + x
2. 5x² - 25x
3. x² - 16
4. x² + 4x + 4
5. x² - 5x + 6
Problem: Factor each of the quadratic expression
Solution:
A quadratic expression is an expression whose highest power is two.
1. x² + x
For this expression:
x² + x
Factorizing x since it is a common term;
x(x + 1)
2. 5x² - 25x
For this expression;
Factorize 5x since it common to both of them;
5x(x - 5)
3. x² - 16
For this expression;
Apply the differences of two squares;
x² - 16
x² - 4²;
Note; x² - y² = (x-y)(x+y)
So, x² - 4² = (x-4)(x + 4)
4. x² + 4x + 4
To solve this,
Find two numbers whose product will be 4 and sum also 4;
x² + 4x + 4 = x² + 2x + 2x + 4
= x(x + 2) + 2(x + 2)
= (x + 2)(x + 2)
5. x² - 5x + 6
To factorize this expression, simply find two numbers whose sum is -5 and product is 6;
x² - 5x + 6 = x² - 3x - 2x + 6
= x (x - 3) -2(x - 3)
= (x -2)(x-3)
(0, 15)
(15, 0)
(4.8)
(10.0)
Which ones are solutions
Answers
Answer:
For which questions dud
A neighborhood is trying to set up school carpools, but they need to determine the number of students who need to travel to the elementary school (ages 5-10), the middle school (ages 11-13), and the high school (ages 14-18). A histogram summarizes their findings:
Histogram titled Carpool, with Number of Children on the y axis and Age Groups on the x axis. Bar 1 is 5 to 10 years old and has a value of 3. Bar 2 is 11 to 13 years old and has a value of 7. Bar 3 is 14 to 18 years old and has a value of 4.
Which of the following data sets is represented in the histogram?
{3, 3, 3, 7, 7, 7, 7, 7, 7, 7, 4, 4, 4, 4}
{5, 10, 4, 11, 12, 13, 12, 13, 12, 11, 14, 14, 19, 18}
{5, 6, 5, 11, 12, 13, 12, 13, 14, 15, 11, 18, 17, 13}
{3, 5, 10, 11, 13, 7, 18, 14, 4}
Answers
The correct answer is that the data set {3, 7, 4} is represented in the given histogram.(option-a)
The given histogram represents the number of children in each age group who need to travel to school. Since the histogram has only three bars, we can conclude that there are only three age groups.
The first bar represents children aged 5-10, of which there are 3. The second bar represents children aged 11-13, of which there are 7. The third bar represents children aged 14-18, of which there are 4.
Therefore, the data set that is represented in the histogram is:
{3, 7, 4}
None of the other data sets given match the values in the histogram. The first data set has duplicate values and is not sorted by age group. The second data set includes ages that are not represented in the histogram. The third data set has values for ages 6, 11, 12, 13, 14, 15, 17, and 18, but the histogram does not have bars for all those ages. (option-a)
For such more questions on histogram
https://brainly.com/question/32761368
#SPJ8
I need help from anybody that knows classkick
DUE
Answers
Answer:
196
Step-by-step explanation:
Answer:
196
Step-by-step explanation:
If you have a quadratic equation in standard form and it has values of a=4, b = -8 and c = -60, what would the equation look like if you factored it out completely
Answers
The quadratic equation so formed will be \(x^{2}\) - 2x - 15 = 0.
What is a quadratic equation?
Any algebraic equation that can be expressed in standard form as where x represents an unknown value and where a, b, and c represent known values, where a 0 is a quadratic equation.
We know that the standard form of a quadratic equation is represented as: a\(x^{2}\) + bx + c = 0.
Here, we are given a = 4, b = -8 and c = -60.
On substituting these values, we get
⇒ a\(x^{2}\) + bx + c = 0
⇒ 4\(x^{2}\) - 8x - 60 = 0
On dividing both sides by 4, we get
⇒ \(x^{2}\) - 2x - 15 = 0
Hence, the quadratic equation so formed will be \(x^{2}\) - 2x - 15 = 0.
Learn more about quadratic equation from the given link
https://brainly.com/question/1214333
#SPJ1
A full can of paint contains 4/5 of a gallon. Brandon used 3/4 of a can of paint to paint a doghouse. He then used 2/3 of what remained in the can to paint a door. How much paint is left in the can,in gallons?
Answers
Answer:
1/60 gallon
Step-by-step explanation:
You want to know what is left of 4/5 gallon of paint if 3/4 gallon was used to paint a doghouse, and 2/3 of the remaining amount was used to paint a door.
Amount remainingTo find the amount remaining we subtract the amount used for the doghouse from the original amount:
4/5 -3/4 = (16 -15)/20 = 1/20 . . . . . gallon
2/3 of that was used, so 1/3 of it remains:
(1/3)(1/20 gallon) = 1/60 gallon
There is 1/60 of a gallon of paint left in the can.
__
Additional comment
In a standard size gallon paint can, that's about 0.11 inches of paint in the bottom.
<95141404393>
