2x – 1 < 11
What is the solution to this equation?
Answers
Answer: x < 6
Step-by-step explanation:
1. Add 1 to both sides of the equation.
2x − 1 + 1 < 11 + 1
2x < 12
2. Divide both sides of the equation.
\(\frac{2x}{2}\) < \(\frac{12}{2}\)
Related Questions
I need help please!!!

Answers
Evaluate f(3)
f(3) = 4(3)-2 = 12 - 2 = 10
f(3) = 10
f(x) = 6 = 4x- 2
4x=8
x = 2
Let f (x) = 3x − 1 and ε > 0. Find a δ > 0 such that 0 < ∣x − 5∣ < δ implies ∣f (x) − 14∣ < ε. (Find the largest such δ.) What limit does this prove?
Answers
Answer:
This proves that f is continous at x=5.
Step-by-step explanation:
Taking f(x) = 3x-1 and \(\varepsilon>0\), we want to find a \(\delta \) such that \(|f(x)-14|<\varepsilon\)
At first, we will assume that this delta exists and we will try to figure out its value.
Suppose that \(|x-5|<\delta\). Then
\(|f(x)-14| = |3x-1-14| = |3x-15|=|3(x-5)| = 3|x-5|< 3\delta\).
Then, if \(|x-5|<\delta\), then \(|f(x)-14|<3\delta\). So, in this case, if \(3\delta \leq \varepsilon\) we get that \(|f(x)-14|<\varepsilon\). The maximum value of delta is \(\frac{\varepsilon}{3}\).
By definition, this procedure proves that \(\lim_{x\to 5}f(x) = 14\). Note that f(5)=14, so this proves that f is continous at x=5.
A block is 20 cm long 12 cm wide and 5cm high Find the volume of 40 such blocks
Answers
Answer:
Find the volume of a concrete block that is 2.5 metres long,. 12 centimetres wide and. 10 centimetres high. Two of the dimensions, the width and height,
Answer:
480,000 cm3
Step-by-step explanation:
give crown please ( brainliest )
) y=-3x - 3
How do you solve this ?

Answers
Answer:
the slope is -3 and the y intercept is -3 because in this type of equation, the equation y=mx+b, the slope is m and the y-intercept is b
Step-by-step explanation:
Solve for z…. Z - 1/5=7/10
Answers
find the value of w. round to the nearest tenth

Answers
Answer:
\(\pmb {w=13.11}\)Step-by-step explanation:
\(\pmb {sin(22)^o=\cfrac{x}{35} }\)
\(\pmb {35sin(22)=w}\)
\(\pmb {w=13.11}\)
_________________
Hope this helps!
Have a great day! :)
c. using systematic random sampling, every fifth dealer is selected starting with the third dealer in the list. which dealers are included in the sample?
Answers
The dealers included in the sample are dealers 3, 8, 13, 18, 23, 28, 33, 38, 43, 48, 53, 58, 63, 68, 73, 78, 83, 88, 93, and 98.
How to find dealers that included in the sample?To use systematic random sampling, we need to choose a starting point and a sampling interval. In this case, we are starting with the third dealer in the list, so we need to skip the first two dealers.
Let's assume that the dealers are numbered 1 to 100 in the list. Since we are starting with the third dealer, our starting point is dealer 3. We also need to choose a sampling interval of 5, since we want to select every fifth dealer.
To find out which dealers are included in the sample, we can use the following formula:
Sampled Dealers = Starting Point + (Sampling Interval * Number of Samples)
Using the formula, we can calculate the dealers that are included in the sample as follows:
Sampled Dealers = 3 + (5 * n)
where n is the number of samples.
If we want to select a sample of 20 dealers, we can substitute n = 1 to 20 into the formula to get the following list of dealers:
3, 8, 13, 18, 23, 28, 33, 38, 43, 48, 53, 58, 63, 68, 73, 78, 83, 88, 93, 98
Therefore, the dealers included in the sample are dealers 3, 8, 13, 18, 23, 28, 33, 38, 43, 48, 53, 58, 63, 68, 73, 78, 83, 88, 93, and 98.
Learn more about Systematic random sampling
brainly.com/question/24317913
#SPJ11
Complete the following steps on the graph:
1) Draw the line x = -3 in black
2) Reflect ABC over the line x = -3 (draw on the graph in blue)
3) Translate A'B'C' by the directed line segment from (0,0) to (4,1) (draw on the graph in red)

Answers
so
How would you write 6.5E4
Answers
6.5 x 10^4
Or
65000
ASAP PLEASEEE HELPPP PLEASEEEE
1.If the parent function f(x) = |x| is transformed to h(x) = |x| - 3, what transformation occurs from f(x) to h(x)?
A.Shift left 3 units
B.Shift right 3 units
C.Shift up 3 units
D.Shift down 3 units
2. If the parent function f(x) = |x| is transformed to h(x) = |x| - 3, how is the vertex affected? Select all that apply.
A.The vertex will not change.
B.The vertex will shift right 3 units.
C.The vertex will shift left 3 units.
D.The vertex will shift up 3 units.
E.The vertex will shift down 3 units.
F.The vertex will not move up or down.
G.The vertex will not move right or left.
3. If the parent function f(x) = |x| is transformed to h(x) = |x| - 3, how is the range affected?
A.The range will not change.
B.The range will be all real numbers.
C.The range will change from y ≥ 0 to y ≥ -3.
D.The range will change from x ≥ 0 to x ≥ -3.
Answers
1) A translation of 3 units down, option D.
2) The vertex moves 3 units down.
3) The new range is y ≥ -3, correct option is C.
Which transformation is applied?For a function f(x) a vertical shift of N units is written as:
g(x) = f(x) + N
In this case, we have:
f(x) = |x|
h(x) = |x| - 3
Then h(x) = f(x) - 3
This is a shift of 3 units down, the correct option is D.
How is the vertex affected?
The vertex is translated 3 units down, like the whole graph of the function.
How is the range affected?
The vertex defines the minimum of the range, so if the vertex goes 3 units down, then the range also does, the new range will be:
y ≥ -3.
So the correct option is C.
Learn more about translations:
https://brainly.com/question/24850937
#SPJ1
A recent survey was conducted to compare the cost of solar energy to the cost of gas or electric energy. Results of the survey revealed that the distribution of the amount of the monthly utility bill of a 3-bedroom house using gas or electric energy had a mean of $91 and a standard deviation of $8. If the distribution can be considered mound-shaped and symmetric, what percentage of homes will have a monthly utility bill of more than $83?
Answers
Answer:
Using a standard normal distribution table, we can find that the percentage of homes that have a monthly utility bill of more than $83 is approximately 13.6%.
Step-by-step explanation:
If the distribution of the monthly utility bill for gas or electric energy can be considered mound-shaped and symmetric, we can use the standard normal distribution table to find the percentage of homes that have a monthly utility bill of more than $83.
To use the standard normal distribution table, we need to standardize the variable by subtracting the mean and dividing by the standard deviation:
(83 - 91) / 8 = -0.875
This means that a monthly utility bill of $83 is 0.875 standard deviations below the mean.
Using a standard normal distribution table, we can find that the percentage of homes that have a monthly utility bill of more than $83 is approximately 13.6%.
For each function, graph the function and its inverse. If the inverse is a function, state the domain and range.
a. f(x)=2/(3x)-4
b. f(x)=2x²-1
c. f(x)=1/(x-1)
Answers
The inverse of the functions are f⁻¹(x) = 2/[3(x + 4)], f⁻¹(x) = √[(x + 1)/2] and f⁻¹(x) = 1/x + 1
How to determine the inverse of the functions?Function (a)
This function is given as
f(x)=2/(3x) - 4
The function needs to be represented as an equation
So, we have
y = 2/(3x) - 4
Swap the positions of x and y
x = 2/(3y) - 4
So, we have
2/(3y) = x + 4
Take the reciprocal of both sides
3y/2 = 1/(x + 4)
Multiply both sides by 2/3
y = 2/[3(x + 4)]
So, the inverse function is
f⁻¹(x) = 2/[3(x + 4)]
The inverse is a function with the domain x ≠ -4 and range of f(x) ≠ 0
See attachment 1 for the graphs
Function (b)
This function is given as
f(x) = 2x² - 1
The function needs to be represented as an equation
So, we have
y = 2x²- 1
Swap the positions of x and y
x = 2y² - 1
So, we have
2y²= x + 1
Divide both sides by 2
y²= 1/2(x + 1)
Take the square roots
y= √[(x + 1)/2]
So, the inverse function is
f⁻¹(x) = √[(x + 1)/2]
The inverse is a function with the domain x ≥ -1 and range of f(x) ≥ 0
See attachment 2 for the graphs
Function (c)
This function is given as
f(x) = 1/(x - 1)
The function needs to be represented as an equation
So, we have
y = 1/(x - 1)
Swap the positions of r and y
x = 1/(y - 1)
So, we have
y - 1 = 1/x
Add 1 to both sides
y = 1/x + 1
So, the inverse function is
f⁻¹(x) = 1/x + 1
The inverse is a function with the domain x ≠ 0 and range of f(x) ≠ 1
See attachment for the graphs
Read more about inverse functions at
brainly.com/question/14796161
#SPJ1

List the elements of the set in roster notation. (enter empty or ∅ for the empty set.) {x | x is a digit in the number 654,323}
__________
Answers
Your answer: {1, 2, 3, 4, 5, 6} in roster notation
To list the elements of the set in, follow these steps:
1. Identify the distinct digits in the number 654,323.
2. Arrange them in roster notation, which means listing them within curly brackets.
The distinct digits in the number 654,323 are 2, 3, 4, 5, and 6.
So, the elements of the set in roster notation are {2, 3, 4, 5, 6}.
learn more about "roster notation":-https://brainly.com/question/26668005
#SPJ11
Please help me respond this question

Answers
The correct options are -
g(x) increases at a faster rate over the interval [1,2].f(x) increases at a faster rate over the interval [0,1]Explain the term rate of increase for function?The pace at which one quantity changes in relation to another quantity is known as the rate of change function. Simply said, the rate of increase is calculated by dividing the amount of growth in one item by the equal number of changes in another.The main concept behind rates of growth is how one variable changes as the other grows. Making tables will make this simple to see.For the stated function.
The graph for the function g(x) is given in the question.
As the slope of function g(x) is most steep for the interval [1,2].
Thus, g(x) increases at a faster rate over the interval [1,2].
The graph for the function f(x) is attached,
f(x) = 3x+ 2
From the graph, it is shown that the slope of the function g(x) is most steep for the interval [0,1].
Thus, f(x) increases at a faster rate over the interval [0,1].
To know more about the rate of increase for function, here
https://brainly.com/question/12614336
#SPJ1

the table shows the number of copies of a newspaper distributed to households in each year from 2008 to 2012 year 2008 2009 2010 2011 2012 number of copies (in thousands) 250 275 290 315 280
Answers
Answer:
The answer to your problem is, in the graph ↓
Step-by-step explanation:
I 400
I 350
I 300————2009(275).2010(290).2011(315).2012(280)
I 250 - 2008(250)
I 100
I 50
I 0
2008 2009 2010 2011 2012
——-——-——-——-——-——-——-——-——-——-——-——-——-——-——-————
Easier:
2008 : 250 ( 250 )
2009: 300 ( 250 )
2010: 300 ( 290 )
2011: 300 ( 315 )
2012: 300 ( 280 )
Parenthesis = Number
Number after “ : “ = Graph on SIDE
First number = Year
Thus the answer is, above!
Do both pls look at the pictures


Answers
(i) Yes, it is even and divisible by 3 as 1 + 0 + 2 = 3
(ii) No, it does not end in 5 or 0
What are Divisibility Rules?
Divisibility criteria can be used to determine whether or not to diminish a fraction. The rules are based on patterns seen while listing the multiples of any integer.
Solution:
(i) 102 is divisible by 6 - TRUE
It is because 102 is even number thus, it is divisible by 2 and since the sum of digits 1 + 0 + 2 is 3 therefore, it is divisible by 3
- Yes, it is even and divisible by 3 as 1 + 0 + 2 = 3
(ii) 102 is divisible by 5 - FALSE
It is because any number to be divisible by 5 it should always end with 5 or 0 at ones place.
- No, it does not end in 5 or 0
To learn more about Divisibility Rules from the given link
https://brainly.com/question/9462805
#SPJ1
Find an equation of the line (in slope-intercept form) that passes through the points (1,2) and (2,3).
Answers
The required equation of the line is y = x + 1
Slope Intercept Form of a line:One of the common ways to describe the equation of a line is in the slope-intercept form of the line. You may use this formula to determine a line's equation given its slope and y-intercept.
The Slope intercept form of a line is y = mx + c,
where m is slope and c is the y-intercept
Here we have
Points (1, 2) and (2, 3)
The Slope intercept form of a line is y = mx + c,
As we know, Slope (m) = (y₂ - y₁)/(x₂ - x₁)
=> Slope of required line = (3 - 2)/(2 - 1) = 1/1 = 1
=> Slope, m = 1
The equation of the line will be: y = (1)x + c,
=> y = x + c
Since (1, 2) passes through the line
=> 2 = 1 + c
=> c = 1
then the equation will be y = x + 1
Therefore,
The required equation of the line is y = x + 1
Learn more about the Slope intercept form at
brainly.com/question/17878329
#SPJ1
Three cell phone towers from APQR. The measure of ZQ
is 10⁰ less than the measure of ZP. The measure of ZR is
5° greater than the measure of ZQ. Which two towers are
the closest together?
Answers
The towers ZQ and ZR are the closest together.
What is triangle?Triangle is a three-sided polygon which has three vertices.
Solution
If the measure of ZP is x,
Then the measure of ZQ is x-10 and the measure of ZR is x-5.
To find the two towers that are closest together, we need to find the minimum value of the difference between any two angles.
ZP and ZQ: x - (x-10) = 10
ZQ and ZR: (x-5) - (x-10) = 5
So, the towers ZQ and ZR are the closest together, with an angle difference of 5°.
Learn more about triangle here: brainly.com/question/27996834
#SPJ1
Sam's Cat Hotel operates 52 weeks per year, 5 days per week, and uses a continuous review inventory system. It purchases kitty litter for $10.75 per bag. The following information is available about these bags. Refer to the standard normal table for z-values. > Demand = 100 bags/week > Order cost = $57/order > Annual holding cost = 30 percent of cost > Desired cycle-service level = 92 percent Lead time = 1 week(s) (5 working days) Standard deviation of weekly demand = 16 bags Current on-hand inventory is 310 bags, with no open orders or backorders.a. What is the EOQ? What would the average time between orders (in weeks)?
b. What should R be?
c. An inventory withdraw of 10 bags was just made. Is it time to reorder?
D. The store currently uses a lot size of 500 bags (i.e., Q=500). What is the annual holding cost of this policy? Annual ordering cost? Without calculating the EOQ, how can you conclude lot size is too large?
e. What would be the annual cost saved by shifting from the 500-bag lot size to the EOQ?
Answers
The required answer is the annual cost saved by shifting from the 500-bag lot size to the EOQ is $1,059.92.
Explanation:-
a. Economic order quantity (EOQ) is defined as the optimal quantity of inventory to be ordered each time to reduce the total annual inventory costs.
It is calculated as follows: EOQ = sqrt(2DS/H)
Where, D = Annual demand = 100 x 52 = 5200S = Order cost = $57 per order H = Annual holding cost = 0.30 x 10.75 = $3.23 per bag per year .Therefore, EOQ = sqrt(2 x 5200 x 57 / 3.23) = 234 bags. The average time between orders (TBO) can be calculated using the formula: TBO = EOQ / D = 234 / 100 = 2.34 weeks ≈ 2 weeks (rounded to nearest whole number).
Hence, the EOQ is 234 bags and the average time between orders is 2 weeks (approx).b. R is the reorder point, which is the inventory level at which an order should be placed to avoid a stockout.
It can be calculated using the formula:R = dL + zσL
Where,d = Demand per day = 100 / 5 = 20L = Lead time = 1 week (5 working days) = 5 day
z = z-value for 92% cycle-service level = 1.75 (from standard normal table)σL = Standard deviation of lead time demand = σ / sqrt(L) = 16 / sqrt(5) = 7.14 (approx)
Therefore,R = 20 x 5 + 1.75 x 7.14 = 119.2 ≈ 120 bags
Hence, the reorder point R should be 120 bags.c. An inventory withdraw of 10 bags was just made. Is it time to reorder?The current inventory level is 310 bags, which is greater than the reorder point of 120 bags. Since there are no open orders or backorders, it is not time to reorder.d. The store currently uses a lot size of 500 bags (i.e., Q = 500).What is the annual holding cost of this policy.
Annual ordering cost. Without calculating the EOQ, how can you conclude the lot size is too large?Annual ordering cost = (D / Q) x S = (5200 / 500) x 57 = $592.80 per year.
Annual holding cost = Q / 2 x H = 500 / 2 x 0.30 x 10.75 = $806.25 per year. Total annual inventory cost = Annual ordering cost + Annual holding cost= $592.80 + $806.25 = $1,399.05Without calculating the EOQ, we can conclude that the lot size is too large if the annual holding cost exceeds the annual ordering cost.
In this case, the annual holding cost of $806.25 is greater than the annual ordering cost of $592.80, indicating that the lot size of 500 bags is too large.e.
The annual cost saved by shifting from the 500-bag lot size to the EOQ can be calculated as follows:Total cost at Q = 500 bags = $1,399.05Total cost at Q = EOQ = Annual ordering cost + Annual holding cost= (D / EOQ) x S + EOQ / 2 x H= (5200 / 234) x 57 + 234 / 2 x 0.30 x 10.75= $245.45 + $93.68= $339.13
Annual cost saved = Total cost at Q = 500 bags - Total cost at Q = EOQ= $1,399.05 - $339.13= $1,059.92
Hence, the annual cost saved by shifting from the 500-bag lot size to the EOQ is $1,059.92.
To know about annual cost . To click the link.
https://brainly.com/question/14784575.
#SPJ11
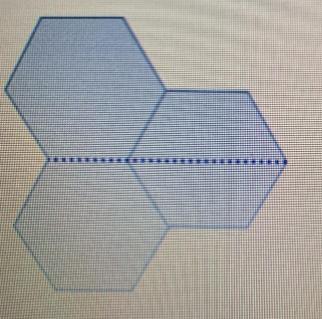
What is the length of the dotted line? round to the nearest hundredth. 2.50 in. 3.75 in. 5.00 in. 6.25 in.
Answers
The measure of the length of the dotted line is 3.75 inches. Then the correct option is B.
What is a hexagon?The hexagon is a 2D geometry that has a 6 number of sides. And all the sides of the polygon are straight lines connected to each other side by side.
The perimeter of the hexagon is 7.5 inches.
Then the length of the hexagon will be
\(\rm 7.5 = 6x\\\\x \ \ = 1.25\)
The length of the hexagon is 1.25 inches.
Then the diagonal length of the hexagon will be
y = 2 × 1.25
y = 2.5
The diagonal length of the hexagon is 2.5 inches.
Then the length of the dotted line is 3.75 inches.
More about the hexagon link is given below.
https://brainly.com/question/3295271
What is the slope of a line that passes through the points (5, 6) and (−11, 14)
Answers
Answer:
m = -1/2
Step-by-step explanation:
let me know if it helped
(too lazy to write a explanation)
Oliver is buying equipment for his restaurant. He can buy two blenders for $396 or three blenders for $479. Find which deal has the best unit price per blender, then record the best unit price!
Answers
Hence, the deal of $\(479\) is best unit price per blender.
What is the equation?
The definition of an equation is a mathematical statement that shows that two mathematical expressions are equal.
Here given that,
Oliver is buying equipment for his restaurant. He can buy two blenders for $\(396\) or three blenders for $\(479\).
So,
Oliver buying two blenders at $\(396\) so the cost of one blender is
i.e., \(\frac{396}{2}=198\)$
Oliver buying two blenders at $\(479\) so the cost of three blenders is
i.e., \(\frac{479}{3}=159\)$
Hence, the deal of $\(479\) is best unit price per blender.
To know more about the equation
https://brainly.com/question/12788590
#SPJ1
Given that triangle RST is isosceles, find the value of ZS

Answers
Answer:
120°
Step-by-step explanation:
\(m\angle S = 180\degree - 2\times 30\degree \\\\
m\angle S = 180\degree - 60\degree \\\\
\huge\purple {\boxed{m\angle S = 120\degree}} \)
a. create a table showing the amount of people knowing the answer to the riddle of the six days (1st sketch a diagram to discover the pattern for this problem)b. state the amount of people to know the answer on day 15.
Answers
The following diagram shows the number of people who know the riddle per day.
The values of x would be from day 1 to 6 while the values of y will be 5, 20, 60, 240, 960, 3840. Thus, we may write the following in the table as follows:
Notice that 5 is always multiplied by a power of 4.
Thus, on day 1, we have
\(5(4^0)=5(1)=5\)On day 2, we have
\(5(4^1)=5(4)=20\)On day 3, we have
\(5(4^2)=5(16)=80\)On day 4, we have
\(5(4^3)=5(64)=320\)On day 5, we have
\(5(4^4)=5(256)=1280\)And on day 6, we have
\(5(4^5)=5(1024)=5120\)Therefore, we may say that the formula to obtain the number of people who know the riddle on x days will be
\(y=5(4^{x-1})\)where y is the number of people and x is the number of days.
Therefore, on the 15th day, we substitute 15 to x in the obtained equation.
\(\begin{gathered} y=5(4^{15-1}) \\ =5\mleft(4^{14}\mright) \\ =5(268,435,456) \\ =1,342,177,280 \end{gathered}\)Therefore, there will be 1,342,177,280 people who will know the answer on the 15th day.


A line has a slope of – 1 and passes through the point ( – 19,17). Write its equation in slope-intercept form.
Answers
\((\stackrel{x_1}{-19}~,~\stackrel{y_1}{17})\hspace{10em} \stackrel{slope}{m} ~=~ - 1 \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{17}=\stackrel{m}{- 1}(x-\stackrel{x_1}{(-19)}) \implies y -17 = - 1 ( x +19) \\\\\\ y-17=-x-19\implies {\Large \begin{array}{llll} y=-x-2 \end{array}}\)
Answer:
y = -x - 2
Step-by-step explanation:
Pre-SolvingWe are given that a line has a slope (m) of -1 and passes through (-19,17).
We want to write the equation of this line in slope-intercept form.
Slope-intercept form is given as y=mx+b, where m is the slope and b is the value of y at the y intercept, hence the name
SolvingAs we are already given the slope of the line, we can plug it into the equation.
Replace m with -1.
y = -1x + b
This can be rewritten to:
y = -x + b
Now, we need to find b.
As the equation passes through (-19,17), we can use its values to help solve for b.
Substitute -19 as x and 17 as y.
17 = -(-19) + b
17 = 19 + b
Subtract 19 from both sides.
-2 = b
Substitute -2 as b into the equation.
y = -x - 2
look at exercise 8. explain how you decided whether the numbers are equivalent
Answers
All the numbers are equal in decimal form, they are equivalent.
To determine if the numbers in Exercise 8 are equivalent, you must compare them using a standard form or convert them to a common form, such as fractions, decimals, or percentages.
Follow these steps to decide whether the numbers are equivalent:
1. Identify the form of the numbers (fractions, decimals, or percentages).
2. If necessary, convert the numbers to a common form for comparison.
3. Compare the converted numbers.
Let's assume the numbers in Exercise 8 are a fraction, a decimal, and a percentage (e.g., 1/2, 0.5, and 50%). To determine if they are equivalent, first, convert them all to the same form:
1. Convert the fraction (1/2) to a decimal by dividing the numerator by the denominator: 1 ÷ 2 = 0.5
2. Convert the percentage (50%) to a decimal by dividing it by 100: 50 ÷ 100 = 0.5
Now that all the numbers are in decimal form, compare them:
1. Compare 0.5 (fraction) to 0.5 (decimal) - they are equal.
2. Compare 0.5 (fraction) to 0.5 (percentage) - they are equal.
3. Compare 0.5 (decimal) to 0.5 (percentage) - they are equal.
Since all the numbers are equal in decimal form, they are equivalent.
To know more about decimal form visit:
brainly.com/question/16361602
#SPJ11
a random sample of 1000 people was taken. 450 of the people in the sample favored candidate a. the 95% confidence interval for the true proportion of people who favor candidate a rounded to three decimal places is:
Answers
The 95% confidence interval for the true proportion of people who favor candidate is (0.419,0.481).
A random sample of 1000 people was condidered for testing.
Number of people in sample favoured candidate
= 450
So, sample proportion, p = 450/1000 = 0.45
Confidence level= 95% i.e, alpha = 1 - 0.95=0.05, From standard normal Z- table, the value of Z( 0.025) is equals to 1.96..
Confidence interval formula,
CL = p ± Z× √(p×(1-p)/n)
Lower bound of interval is ,
=0.45 - 1.96× √(0.45× (1-0.45)/1000)
= 0.45 - 1.96× √(0.45× 0.55/1000)
= 0.45 - 1.96× √(0.0002475)
=0.419165~ 0.419
So the Upper bound is
= p + Z×√(p×(1-p)/n)
= 0.45 + 1.96× √(0.45× (1-0.45)/1000)
= 0.45 + 1.96× √(0.0002475)
= 0.480835 ~0.481
Hence, the required confidence interval is (0.419,0.481).
To learn more about Confidence interval, refer:
https://brainly.com/question/15712887
#SPJ4

Please help.
Click on the picture for better view!

Answers
Answer:
D. (-3;-3)
Step-by-step explanation:
2x-3y<9
A. 2×6-3×(-4)=24 FALSE, because 24>9
B. 2×(-1)-3×(-9)=25 FALSE, because 25>9
C. 2×2-3×(-5)=11 FALSE, because 11>9
D. 2×(-3)-3×(-3)=9 TRUE, because 3<9
4x10 to the 8power/5x10 to the 3power
Answers
The value of the exponent is 80000000000.
What are exponents?Exponentiation is a mathematical operation that involves the base number and the exponent (or power) number (n), and is represented as bn. Its pronunciation is "b (raised) to the (power of) n." Exponentiation corresponds to base multiplication when n is a positive integer; therefore, bn is the result of multiplying n bases: Exponent-related problems are solved using the rules of exponents or the properties of exponents. These characteristics are regarded as major exponents rules that must be adhered to when solving exponents.acc to our question-
4x10 to the 8power/5x10 to the 3power is = 80000000000.learn more about exponents here:
https://brainly.com/question/13669161
#SPJ13
Planes X and Y and points J, K, L, M, and N are shown. Exactly how many planes contain points J, K, and N?
O 0
O 1
O 2
O 3
Answers
Answer:
3
Step-by-step explanation:
I think why but i think
number but