$3,000 is invested in an account that earns 3% annually interest, compounded monthly.
What is the value of the account after 10 years ?
Answers
Given the principal and annual interest rate, the total amount accrued after 10 years is approximately $4,048.06.
What is the amount of money accrued after 10 years?
The compound interest formula is expressed mathematically as;
A = P(1 + r/n)^(n*t)
Where A is amount accrued, P is principal, r is interest rate, n is number of times interest applied per time period and t is time.
Given the data in the question;
Principal P = $3,000Annual interest rate r = 3% = 3/100 = 0.03Compounded monthly n = 12Time t = 10 yearsPlug the given values into the formula above and solve for A.
A = P(1 + r/n)^(n*t)
A = 3000(1 + 0.03/12)^(12 × 10)
A = 3000(1 + 0.0025 )¹²⁰
A = 3000(1.0025 )¹²⁰
A = 3000( 1.34935354 )
A = $4,048.06
Given the principal and annual interest rate, the total amount accrued after 10 years is approximately $4,048.06.
Learn more about compound interest here: brainly.com/question/27128740
#SPJ1
Related Questions
HELP PLSS!! TYYY picture below
A child received 10 building blocks for Christmas. Each block is either 1
inch or 3 inches wide. The child places them next to each other to make a
line 18 inches long. Which system of equations can be used to determine x,
the number of 1-inch-wide blocks in the line, and y, the number of 3-inch-
wide blocks in the line?
C
x + y = 18
x + 3y = 10
x + y = 10
x + 3y = 18
8:2
x + y = 10
3x + y = 18
4
x + y = 18
3x + y = 10
7 points

Answers
The system of equations that can be used to determine a and y are
x+ y=10
x+3y=18
What is meant by an equation?When two expressions are connected with the equals sign (=) in a mathematical formula, it expresses the equality of the two expressions. In English, an equation is defined as a properly written formula that consists of two expressions joined by an equals sign, while cognates of the word in other languages may have slightly different meanings. An equation, for instance, is said to have one or more variables in French.
Determine which values of the variables result in the equality to be true in order to solve an equation with variables. The values of the variables that must fulfill the equality to constitute the answer are known as the unknowns, together with the variables for which the equation must be solved.
Let x be the number of blocks of one inch
And y be the number of three inch blocks
The number of blocks must be 10
Therefore, x+y=10
The length of the line is 18 inches long.
So, x+3y=18
Therefore, x+ y=10
x+3y=18
To know more about equation, visit:
https://brainly.com/question/29657983
#SPJ1
Solve each initial value problem with Discontinuous Forcing Functions
And use Laplace transform
y"+4y'+5y=2u_3 (t)-u_4(t) t. y(0) = 0, y'(0) = 4
Answers
The inverse Laplace transform of 8/(s + 2)² is \(8te^{(-2t)}\)
The solution y(t) to the given initial value problem is:
\(y(t) = 1 - 2e^{(-2t)} + 8te^{(-2t)\)
To solve the given initial value problem using Laplace transforms, we will first take the Laplace transform of both sides of the differential equation.
Then we will solve for the Laplace transform of the unknown function Y(s).
Finally, we will take the inverse Laplace transform to obtain the solution in the time domain.
The Laplace transform of the second derivative y" of a function y(t) is given by:
\(L\{y"\} = s^2Y(s) - sy(0) - y'(0)\)
The Laplace transform of the first derivative y' of a function y(t) is given by:
\(L\{y'\} = sY(s) - y(0)\)
The Laplace transform of a constant multiplied by a unit step function u_a(t) is given by:
\(L\{c * u_a(t)\} = (c / s) * e^_(-as)\)
Applying these transforms to the given differential equation:
\(L\{y"+4y'+5y\} = L\{2u_3(t)-u_4(t)\} - t\)
\(s^2Y(s) - sy(0) - y'(0) + 4(sY(s) - y(0)) + 5Y(s) = 2/s * e^{\{(-3s)\}} - 1/s * e^{(-4s)} - (1 / s^2)\)
Using the initial conditions y(0) = 0 and y'(0) = 4:
\(s^2Y(s) - 4s + 4sY(s) + 5Y(s) =\) \(2/s * e^{(-3s)} - 1/s * e^{(-4s)} - (1 / s^2)\)
Combining like terms:
\(Y(s)(s^2 + 4s + 5) = 2/s * e^{(-3s)} - 1/s * e^{(-4s)} - (1 / s^2) + 4s\)
Factoring the quadratic term:
\(Y(s)(s + 2)^2 = 2/s * e^(-3s) - 1/s * e^{(-4s)} - (1 / s^2) + 4s\)
Now, solving for Y(s):
\(Y(s) = [2/s * e^{(-3s)} - 1/s * e^{(-4s)} - (1 / s^2) + 4s] / [(s + 2)^2]\)
To find the inverse Laplace transform of Y(s), we will use partial fraction decomposition.
The expression \((s + 2)^2\) can be written as (s + 2)(s + 2) or (s + 2)².
Let's perform partial fraction decomposition on Y(s):
\(Y(s) = [2/s * e^{(-3s)} - 1/s * e^{(-4s)} - (1 / s^2) + 4s] / [(s + 2)^2] = A/s + B/(s + 2) + C/(s + 2)^2\)
Multiplying through by the common denominator (s²(s + 2)²):
\(2(s + 2)^2 - s(s + 2) - (s + 2)^2 + 4s(s + 2)^2 = As(s + 2)^2 + Bs^2(s + 2) + Cs^2\)
Simplifying the equation:
\(2(s^2 + 4s + 4) - s^2 - 2s - s^2 - 4s - 4 - s^2 - 4s - 4 = As^3 + 4As^2 + 4As + Bs^3 + 2Bs^2 + Cs^2\)
\(2s^2 + 8s + 8 - 3s^2 - 10s - 4 = (A + B)s^3 + (4A + 2B + C)s^2 + (4A)s\)
Grouping the terms:
\(-s^3 + (A + B)s^3 + (4A + 2B + C)s^2 + (4A + 2B - 2)s = 0\)
Comparing the coefficients of like powers of s, we get the following equations:
1 - A = 0 (Coefficient of s³ term)
4A + 2B + C = 0 (Coefficient of s² term)
4A + 2B - 2 = 0 (Coefficient of s term)
Solving these equations, we find:
A = 1
B = -2
C = 8
Substituting these values back into the partial fraction decomposition:
Y(s) = 1/s - 2/(s + 2) + 8/(s + 2)²
Now we can take the inverse Laplace transform of Y(s) using the table of Laplace transforms:
\(L^{-1}{Y(s)} = L^{-1}{1/s} - L^{-1}{2/(s + 2)} + L^{-1}{8/(s + 2)^2}\)
The inverse Laplace transform of 1/s is simply 1. The inverse Laplace transform of,
\(2/(s + 2)\ is\ 2e^{(-2t)\)
The inverse Laplace transform of 8/(s + 2)² is \(8te^{(-2t)}\)
Therefore, the solution y(t) to the given initial value problem is:
\(y(t) = 1 - 2e^{(-2t)} + 8te^{(-2t)\)
To know more about Laplace transforms visit:
https://brainly.com/question/30759963
#SPJ11
The initial value problem involves a second-order linear homogeneous differential equation with discontinuous forcing functions. The differential equation is given by y"+4y'+5y=2u₃(t)-u₄(t) t, where y(0) = 0 and y'(0) = 4.
To solve this problem using Laplace transforms, we take the Laplace transform of both sides of the equation, apply the initial conditions, solve for the Laplace transform of y(t), and finally take the inverse Laplace transform to obtain the solution in the time domain.
Using the Laplace transform, the given differential equation becomes
(s²Y(s) - sy(0) - y'(0)) + 4(sY(s) - y(0)) + 5Y(s) = 2e^(-3s)/s - e^(-4s)/s².
Substituting the initial conditions, we have
(s²Y(s) - 4s) + 4(sY(s)) + 5Y(s) = 2e^(-3s)/s - e^(-4s)/s².
Simplifying the equation, we get
Y(s) = (4s + 4)/(s² + 4s + 5) + (2e^(-3s)/s - e^(-4s)/s²)/(s² + 4s + 5).
To find the inverse Laplace transform, we can use partial fraction decomposition and inverse Laplace transform tables. The inverse Laplace transform of Y(s) will yield the solution y(t) in the time domain. Due to the complexity of the equation, the explicit form of the solution cannot be determined without further calculations.
Therefore, by applying Laplace transforms and solving the resulting algebraic equation, we can obtain the solution y(t) to the initial value problem with discontinuous forcing functions.
To learn more about differential equation refer:
https://brainly.com/question/18760518
#SPJ11
An experiment involves selecting a random sample of 256 middle managers for study. One item of interest is annual income. The sample mean is computed to be £35,420, and the sample standard deviation is £2,050. a) What is the estimated mean income of all middle managers (the population)? b) Give a 95 percent confidence interval (rounded to the nearest £10) for your estimate of the mean income. Do you have to make any assumptions? c) Interpret the meaning of the confidence interval.
Answers
a)The sample is random and representative, we can assume that the sample mean is a good estimate of the population mean. b) the critical value is 1.96 (approximately). c)The confidence interval provides a measure of the uncertainty associated with our estimate of the population mean income.
a) The estimated mean income of all middle managers (the population) can be obtained by using the sample mean as an estimate. In this case, the sample mean is £35,420. Since the sample is random and representative, we can assume that the sample mean is a good estimate of the population mean.
b) To determine a 95 percent confidence interval for the estimate of the mean income, we need to consider the sample size, sample mean, and sample standard deviation.
With a sample size of 256, we can assume that the sampling distribution of the sample mean is approximately normally distributed. Given the sample mean of £35,420 and the sample standard deviation of £2,050, we can calculate the margin of error using the formula:
Margin of Error = (Critical Value) * (Standard Error)
Since we want a 95 percent confidence interval, the critical value is 1.96 (approximately). The standard error is calculated by dividing the sample standard deviation by the square root of the sample size.
Once we have the margin of error, we can construct the confidence interval by subtracting and adding the margin of error to the sample mean.
c) The confidence interval provides a range of values within which we are 95 percent confident that the population mean lies. In this case, the confidence interval for the mean income would be expressed as (£Lower Bound, £Upper Bound).
This means that we can be 95 percent confident that the true population mean income falls within this interval.
It is important to note that this interval is specific to this sample and may differ if another random sample is taken. The confidence interval provides a measure of the uncertainty associated with our estimate of the population mean income.
Learn more about confidence interval here
https://brainly.com/question/32546207
#SPJ11
Two window washers start at the heights shown. One is rising, the other is descending. How long does it take for the two window washers to reach the same height? Explain.
Answers
Answer:
After 18.32 seconds washer men will be at the same height.
Step-by-step explanation:
Given question is incomplete; here is the complete question.
Two window washers start at the heights shown. (A: 21 ft high rising 8 in per second. The other is 50 feet high descending 11 inches per second) one is rising one is descending. How long does it take for the two window washers to reach the same height? Explain
Two window washers are moving in opposite directions.
First window washer is at 21 ft and rising with the speed of 8 inches per second.
Second window washer is at 50 feet and descending with the speed of 11 inches per second.
Since 1 feet = 12 inches
Therefore, 21 feet = 21×12 = 252 inches
Similarly, 50 feet = 50 × 12 = 600 inches
Let both the window washer takes 't' time to be at the same height.
Height of the first window washer after t seconds = (252 + 8t) feet
Height of the second window washer after t seconds = (600 - 11t) feet
Since both are at the same height after time 't',
(252 + 8t) = (600 - 11t)
8t + 11t = 600 - 252
19t = 348
t = 18.32 seconds
Therefore, after 18.32 seconds washer men will be at the same height.
of the 80 students who signed up for after school clubs , 16 students signed up for the art club and the the other one signed up for different clubs find the ratio of the number of students who signed up for art club and student who sighned up for other clubs express your answer in simplest form
Answers
Answer:
Ratio of student who signed up for art club:
1/5
Ratio who signed other club:
4/5
Step-by-step explanation:
First find out ratio who signed up for art club
you have 16 out of 80
find the common factor: 16
16/16 = 1
80/16 = 5
so 1/5
other clubs is the rest so 5/5 - 1/5 = 4/5
please give thanks :)
is m < 5 = 57, what is m < 3?

Answers
Answer:
m∠3 = 123
Step-by-step explanation:
57 + x = 180
x = 123
For a school project two students shona and miguel record the number of text messgaes each of them sent each day for 60- day period. the box plots summarize the record data
Answers
The range of the data for Shona and Miguel will be 35 and 30, while the median of the data will be 40 and 42.5.
What is a boxplot?A boxplot is a visual representation of a data set's dispersion and centers.
The interquartile range and the mean of the data set are two examples of spread measures. The mean, average, and median are examples of center measures.
The data set of the Miguel is;
25,30,35,40,45,50,55
The median of the data is;
\(\rm Median =( \frac{n+1}{2}) ^{th} term \\\\ Median =( \frac{7+1}{2} )^{th} term \\\\ Median = 4 ^{th} term \\\\ Median = 40\)
Shona's data is;
25,30,35,40,45,50,55,60
The median of Miguel's data is;
\(\rm Median_{shona} = \rm \frac{40+45}{2} \\\\ Median_{shona} =42.5\)
The range of Miguel's data is;
⇒ 55-25
⇒ 30
The range of Shona's data is;
⇒60-25
⇒35
Hence, the median of the data for Shona and Miguel will be 40 and 42.5 and the range of the data for Shona and Miguel will be 35 and 30.
To learn more about the box plot, refer to https://brainly.com/question/1523909.
#SPJ1

solve for x
x(2x+1)=0
Answers
Answer:
x = 0, -1/2
Step-by-step explanation:
x(2x+1)=0
2x^2 + x = 0
x(2x+1) = 0
x = 0, -1/2
h(x)=x^2-1 what is the average rate of change of h over the interval −3≤x≤−1
Answers
\(slope = m = \cfrac{rise}{run} \implies \cfrac{ f(x_2) - f(x_1)}{ x_2 - x_1}\impliedby \begin{array}{llll} average~rate\\ of~change \end{array}\\\\[-0.35em] \rule{34em}{0.25pt}\\\\ h(x)=x^2-1 \qquad \stackrel{-3\leqslant ~~x~~\leqslant -1}{\begin{cases} x_1=-1\\ x_2=-3 \end{cases}}\implies \cfrac{h(-3)-h(-1)}{-3-(-1)} \\\\\\ \cfrac{[(-3)^2-1]~~ -~~[(-1)^2-1]}{-3+1}\implies \cfrac{8~~-~~0}{-2}\implies -4\)
In the World Cup Downhill held at Panorama Mountain Village in British Columbia, the skiers raced 3514 m down the mountain. If the vertical height of the course was 984 m, determine the average angle of the ski course with the ground.
Answers
Answer:
16.3°
Step-by-step explanation:
This question above is a Trigonometry question that is solved using the formula of Sine
sin θ = Opposite/Hypotenuse
Opposite = The vertical height of the course = 984 m
Hypotenuse = The distance the skiers raced down the mountain = 3514 m
θ = The average angle of the ski course with the ground = ?
sin θ = 984 m/3514 m
sin θ = 0.2800227661
θ = arc sin (0.2800227661)
= 16.261563463°
≈ 16.3°
Therefore, the average angle of the ski course with the ground is 16.3°
To find x and how to do it

Answers
Answer:
Step-by-step explanation:
teorema de pitagoras
Suppose your math teacher was running for Governor. In a pre-election poll of 750 people, the estimate (called a point estimate) was 40%, meaning that 40% of the people would vote for your math teacher. Suppose there was a 4% margin of error. How many people (out of 750) said they would vote for your math teacher? Show your work. Write the answer as a complete sentence.
Answers
Solution
- 40% of peole would vote for the mMath teacher out f the 750 people. This implies that the number of people tahat would vote for him is
\(\begin{gathered} 40\%\times750 \\ \frac{40}{100}\times750=300\text{ people} \end{gathered}\)- We are also told that there is a margin of error of 4%. This implies that the number of people that vote for the math teacher is either 4% more or 4% less than the 300 people
- 4% margin of error can be gotten as follows:
\(\frac{4}{100}\times750=30\)- Thus, the number of people that vote for him is 300 give or take 30 people
a company just announced that it has made a profit £4 million. It is going to give 2/7 of this to charity. How much will it give to charity?
Answers
Answer:
Approximately- 1142857 pounds.
Step-by-step explanation:
Just multiply 4M (6 zeros), with proportion:
(4*10^6)*(2/7)= the answer that i've gave you
i’m confused and would love help.

Answers
The final equation of the line is y = (-2/3)x - 3 in the coordinate system.
what is coordinate system?
A coordinate system is a system that uses one or more numbers or coordinates to uniquely determine the position of a point or an object in space. In mathematics, the most common coordinate system is the Cartesian coordinate system
what is equation ?
In mathematics, an equation is a statement that shows the equality between two expressions. It contains an equals sign (=) between the two expressions that are being compared. Equations can be used to describe relationships between variables, to solve problems, or to represent real-world situations.
In the given question,
To draw the line going through (-6,1) with a slope of -2/3, we can follow these steps:
Plot the point (-6,1) on a coordinate system. This will be one point on the line.
From that point, use the slope to find another point on the line. A slope of -2/3 means that for every 3 units to the right we move, we must move 2 units down. So starting from (-6,1), we can move 3 units to the right and 2 units down to get to the point (-3,-1). This is another point on the line.
Draw a straight line through the two points to represent the line going through (-6,1) with a slope of -2/3.
To write the equation of the line, we can use the point-slope form of the equation:
y - y1 = m(x - x1)
where (x1,y1) is one point on the line, m is the slope, and (x,y) are the coordinates of any other point on the line. Let's choose (-6,1) as our point:
y - 1 = (-2/3)(x - (-6))
Simplifying, we get:
y - 1 = (-2/3)x - 4
Adding 1 to both sides, we get the final equation of the line:
y = (-2/3)x - 3
To know more about coordinate system, visit:
https://brainly.com/question/29762404
#SPJ1
pls help if you can asap!!!!

Answers
Answer: A
Step-by-step explanation: I would say A because the angle is greater than 90 degrees
Answer:
We have supplementary angles.
76 + 3x + 2 = 180
3x + 78 = 180
3x = 102
x = 34
The diagram shows an open rectangular box ABCDEFGH.
A straight stick AGM rests against A and G and extends outside the box to M.
a. Calculate the angle between the stick and the base of the box.
b. AM= 30 cm.
Show that GM= 4.8 cm, correct
to 1 decimal place.

Answers
The angle between the stick and the base of the box is 77. 9 degrees
How to determine the angleTo determine the angle between the stick and the base, we have to know the trigonometric identities.
These identities are;
sinecosinecotangenttangentsecantcosecantFrom the information given, we have;
sin A = FB/AB
Given that;
GB = 14.5cm
AB = 18. 6cm
substitute for the length of the sides, we have;
sin A = 14.5/18. 6
Divide the values, we have;
sin A = 0. 7796
Find the inverse sine
A = 77. 9 degrees
Learn more about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
Residents of the town of Maple Grove who are connected to municipal water supply are billed a fixed amount yearly plus a charge for each cubic foot of water used. A household using 1000 cubic feet was billed $90, while one using 1600 cubic feet was billed $105. What is the charge per cubic foot? How do you wite an equation for the total cost of a residen'ts water as a function of cubic feet of water used? How many cubic feet of water used would lead to a bill of $130. I am lost from the beginning of how to start this problem.
Answers
The charge per cubic foot is $0.05. The equation for the total cost of a resident's water is C(x) = 0.05x + 40. The number of cubic feet of water used that would lead to a bill of $130 is 2200.
We will use the given data to calculate the charge per cubic foot:Let x be the number of cubic feet of water used by a household and let y be the corresponding bill amount.
Case 1: When a household using 1000 cubic feet was billed $90.
Case 2: When one using 1600 cubic feet was billed $105.Subtracting case 1 from case 2, we get:$$105 - 90 = 15$$$$1600 - 1000 = 600$$So, the charge per cubic foot is:$$\frac{15}{600} = 0.025$$$$\implies 0.05 \text{ (for two decimal place)}$$ Hence, the charge per cubic foot is $0.05.
To write an equation for the total cost of a resident's water as a function of cubic feet of water used, we will use the given data:
$$\text{Fixed amount = } $40$$\text{Charge per cubic foot of water used = } $0.05$$\text{Number of cubic feet used = } x$$
Therefore, the equation for the total cost of a resident's water as a function of cubic feet of water used is:
$$C(x) = \text{(Charge per cubic foot of water used)}\times\text{(Number of cubic feet used)}+\text{(Fixed amount)}$$$$C(x) = 0.05x + 40$$
To find out how many cubic feet of water used would lead to a bill of $130, we will use the equation obtained above:
$$C(x) = 0.05x + 40
= $130$$$$\implies 0.05x
= $90$$$$\implies x
= \frac{90}{0.05}
= 1800$$
Therefore, the number of cubic feet of water used that would lead to a bill of $130 is 1800.
To know more about resident's water, visit
https://brainly.com/question/30332520
#SPJ11
Not all variables retained in a regression model are required to be significant.
True or False
Answers
Answer:
True
Step-by-step explanation:
True.
Not all variables retained in a regression model need to be statistically significant at a given level of significance (e.g., 5% level). The inclusion of variables in a regression model can be based on theoretical or practical considerations, and not solely on statistical significance. Moreover, some variables may have an important effect on the dependent variable even if they are not statistically significant in the model. However, it is important to assess the overall fit and predictive power of the model, and to consider alternative models and variable transformations if necessary.
What is the solution to -1 - 7

Answers
Answer:
-8
Step-by-step explanation:
start at -1, move 7 more spots left you get to -8
please hit the heart button :)
Answer:
-8
Step-by-step explanation:
-1 - 7 is pretty much -(1+7) which is -8.
When adjusting accrual earnings to obtain cash flows from operations, an increase in Prepaid Rent Expense is subtracted to arrive at cash flow from operations. Group startsTrue or False
Answers
False, an increase in Prepaid Rent Expense is not subtracted when adjusting accrual earnings to obtain cash flows from operations.
When adjusting accrual earnings to obtain cash flows from operations using the indirect method, an increase in Prepaid Rent Expense is not subtracted. Prepaid Rent Expense represents an amount that has been paid in advance for future rent expenses. It is considered a cash outflow when it is initially paid, but it is not directly related to the operating activities of the business.
To arrive at cash flows from operations, the adjustments involve converting net income from an accrual basis to a cash basis. This includes accounting for non-cash expenses, such as depreciation and amortization, and changes in working capital accounts, such as accounts receivable, accounts payable, and inventory.
Learn more about subtracted here:
https://brainly.com/question/13619104
#SPJ11
Question 5 Find the integral of this function: f(x) = e5x dx 00 01 e5a 52 0-e5 0-e 5e5z -5x -5e5z e + C Oer + C 0-e52 +0 0-e5+C 5e5z + C -5e5z + C 20 pts
Answers
The integral of f(x) = \(e^5^x\) with respect to x is \(\frac{1}{5}*e^5^x+C\), where C is a constant.
To obtain the integral of the function f(x) = \(e^5^x\), we can use the basic rules of integration.
The integral of \(e^k^x\) with respect to x is given by \(\frac{1}{k}*e^k^x+C\), where C is the constant of integration.
In this case, the coefficient of x is 5, so we have k = 5.
Using the formula, the integral of \(e^5^x\) with respect to x is:
\(\frac{1}{5}*e^5^x+C\)
This is the antiderivative of f(x), also known as the indefinite integral.
The "+ C" represents the constant of integration, which allows for the existence of an infinite family of antiderivatives.
To know more about integral refer here:
https://brainly.com/question/31059545#
#SPJ11
Please help me with this question!!

Answers
Answer:
1. No
2. yes
3.yes
4.no
Step-by-step explanation:
Just fill in the blank it's more of a put it in and see if it works kind of problem.
You rent an apartment that costs $1700 per month during the first year, but the rent is set to go up 9% per year. What would be the rent of the apartment during the 12th year of living in the apartment? Round to the nearest tenth (if necessary).
Answers
Given :
You rent an apartment that costs $1700 per month during the first year, but the rent is set to go up 9% per year.
To Find :
The rent of the apartment during the 12th year of living in the apartment.
Solution :
Let, A is the final price after 12 year and P is the principal amount.
We know, by formula of compounding :
\(A = P( 1 + \dfrac{r}{100})^t\\\\A = 1700( 1 + \dfrac{9}{100} )^{12}\\\\A = \$4781.53\)
Therefore, the rent of the apartment during the 12th year of living in the apartment is $4781.53 .
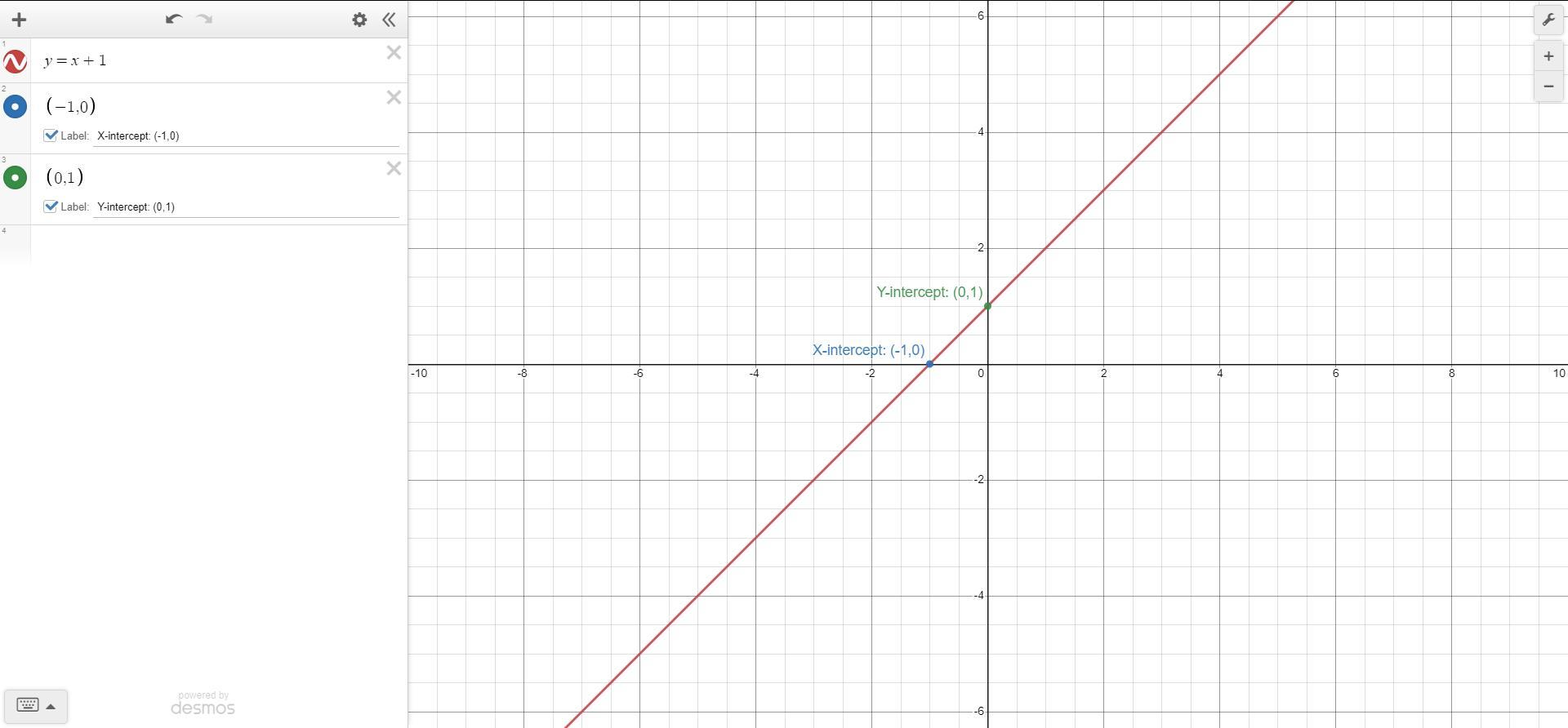
y = x + 1
in graph form
Answers
Answer:
See graph
Step-by-step explanation:
Which of the following lines is parallel to the line that goes through the points (5, 8) and (3, 6)? Please help me!!!!!!
Answers
Answer:
Any line with the slope 1 or y = x + b
Step-by-step explanation:
Parallel lines by definition have the same slope
Value of the y-intercept or b doesn't matter in this case
You have to find the slope of the line through (3,6) and (5,8)
Slope equation is
\(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)Plug in values given
\(\frac{8-6}{5-3}\)
Evaluate
\(\frac{2}{2} =1\)
Any line with the slope of 1 (or no co-efficient in front of x) would be parallel to the line through (3,6) and (5,8)
Find the zeros and the vertical intercept of the function f(x) = -9x³+9x² - 2x. Give your answers as integers or reduced fractions. The zero(s) is/are ______
The horizontal intercept(s) is/are _____
Rhe vertical intercept is _____
Answers
The vertical intercept is (0, 0). Horizontal intercepts are the points where the graph of the function intersects the x-axis. At these points, the value of y is zero.
The function f(x) = -9x³+9x² - 2x can be factored as: -x(9x² - 9x + 2) .
The zeros can be obtained by setting the function equal to zero:-
x(9x² - 9x + 2) = 0
The zeros of the function are 0, 2/9, and 1.
To determine these solutions, we can use the Zero Product Property, which tells us that if the product of two factors is equal to zero, then at least one of the factors must be equal to zero. We can find the zeros of the function by setting each factor equal to zero and solving for x.
Thus, we have:Horizontal intercepts are the points where the graph of the function intersects the x-axis. At these points, the value of y is zero.
To find the horizontal intercepts, we set f(x) = 0 and solve for x.
Thus, we have:-9x³+9x² - 2x = 0x(-9x²+9x - 2) = 0
The horizontal intercepts of the function are -2/3, 0, and 2/3.
To determine these solutions, we can use the Zero Product Property, which tells us that if the product of two factors is equal to zero, then at least one of the factors must be equal to zero.
We can find the horizontal intercepts of the function by setting each factor equal to zero and solving for x.The vertical intercept is the point where the graph of the function intersects the y-axis.
At this point, the value of x is zero. To find the vertical intercept, we set x = 0 and evaluate the function. Thus, we have:
f(0) = 0 - 0 + 0 = 0.
Therefore, the vertical intercept is (0, 0).
To know more about vertical intercept visit :-
https://brainly.com/question/30820723
#SPJ11
whats the lowest common multiple of 120 and 19600
Answers
Answer:
Multiples of 120 are 120, 240, 360, 480, 600, 720, 840 etc; Multiples of 150 are 150, 300, 450, 600, 750, 900 etc; Therefore, the least common multiple of 120 and 150 is 600.
Least common multiple (LCM) of 19600 and 19619 is 384532400.
Answer: 19600
Step-by-step explanation:
19600/120 = 160
Consider the following curve. f(x)= x 2x−4
Find the interval(s) on which f is increasing. (Enter your answer using interval notation.) Find the interval(s) on which f is decreasing. (Enter your answer using interval notation.) Find the interval(s) on which f is concave up. (Enter your answer using interval notation.) Find the interval(s) on which f is concave down. (Enter your answer using interval notation.)
Answers
To determine the intervals where the function f(x) = x/(2x-4) is increasing, decreasing, concave up, and concave down, we need to analyze its derivative and second derivative.
First, let's find the derivative of f(x):
f'(x) = (2x-4)(1) - x(2) / (2x-4)^2
= (2x - 4 - 2x) / (2x-4)^2
= -4 / (2x-4)^2
To find the intervals where f is increasing or decreasing, we need to determine where f'(x) is positive (increasing) or negative (decreasing). Since f'(x) is always negative (-4 / (2x-4)^2 < 0), f(x) is always decreasing.
Next, let's find the second derivative of f(x):
f''(x) = (d/dx) (-4 / (2x-4)^2)
= (-4) (d/dx) (1 / (2x-4)^2)
= (-4) (-2) / (2x-4)^3
= 8 / (2x-4)^3
To find the intervals where f is concave up or concave down, we need to determine where f''(x) is positive (concave up) or negative (concave down). Since f''(x) is always positive (8 / (2x-4)^3 > 0), f(x) is always concave up.
Learn more about function at https://brainly.com/question/31326092
#SPJ11
One of the most common types of volcanoes is called a cylinder cone volcano. These types of volcanoes are the smallest type of volcano, ranging between 300 feet and 1200 feet tall, and are in the shape of a cone.
Find the volume of a cinder cone volcano with a height of 350 feet and a diameter of 1100 feet. Use 3.14 for and round your answer to the nearest cubic foot.
Answers
The volume of a cinder cone volcano will be 110872040 cubic feet.
What is the volume of a cone?The volume of a cone is defined as the amount of space occupied by a cone in a three-dimensional plane.
The volume of the cone (V) = 1/3 πhr²
Given,
Radius of cone (r) = 1100/2 = 550 feet
Height of cone (h) = 350 feet
The volume of a cinder cone volcano = 1/3 πhr²
Substitute the values of h and r,
The volume of a cinder cone volcano = 1/3 × 3.14× (550)² × (350)
The volume of a cinder cone volcano = 110872040 cubic feet.
Thus, the volume of a cinder cone volcano will be 110872040 cubic feet.
Learn more about the volume of the cone here:
brainly.com/question/1578538
#SPJ1
About how many times greater was change in price per gallon in 2007 than 2000? Show your work or explain how u determind your answer.
Answers
The required, in 2007 the price per gallon was 7b more than the price of a gallon of fuel in the year 2000. Where b is the inflation factor.
What is simplification?The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
Here,
Let 'a' be the cost per gallon of fuel in the year 2000, and 'b' be the inflation rate per year. If the rate of inflation is constant then
After 7 year inflation = 7b
Cost of fuel in 2007 = a + 7b
Now,
according to the question
Change in cost of fuel
= cost in 2007 - cost in 2000
= a + 7b - a
= 7b
Thus, the required, in 2007 the price per gallon was 7b more than the price of a gallon of fuel in the year 2000. Where b is the inflation factor.
Learn more about simplification here:
https://brainly.com/question/12501526
#SPJ1