3x+2x-13=47 solve for x
please show all the steps
Answers
See photo I provided below
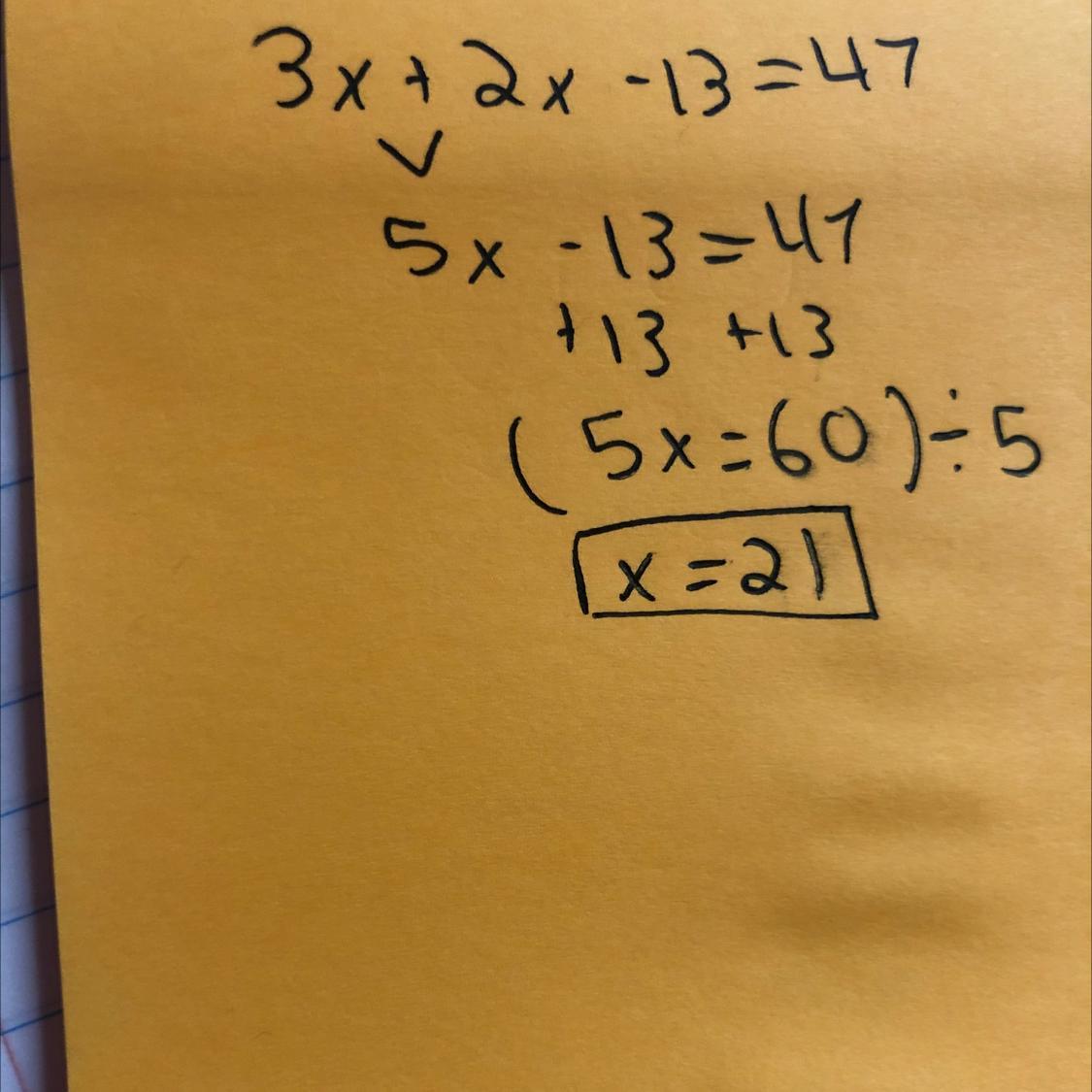
5x-13=47
Add 13 from both side
47+13=60
5x=60
Divide 5x both Side to get x=12
Related Questions
The manager of a company wants to find out how many hours the employees worked in the previous month. Which of the following is a statistical question that the manager can ask?
Answers
It only seeks a single value and does not involve collecting data to draw general conclusions.
Which of the following is a statistical question that the manager can ask?"Which employee worked the most hours in the previous month?" is not a statistical question because it only seeks a single value and does not involve collecting data to draw general conclusions.
On the other hand, "What is the average number of hours worked by employees in the previous month?" is a statistical question because it involves collecting data on all employees and using it to draw general conclusions about the entire workforce.
to know more ABOUT employees
brainly.com/question/21847040
#SPJ1
Find the value that makes each equation true.
A. 110%n=11 n=
B.
(328 x 128) x k = 328 x (82 x 128)
K=
Answers
Answer:
A. \(n=100\)
B. \(k=0\)
Step-by-step explanation:
A. The equation "110% n = 11" can be solved as follows:
110% n = 11
To solve for n, we need to get rid of the percentage sign (%). We can do this by dividing both sides of the equation by 110%, or 0.110 (since 110% is equivalent to 1.1 in decimal form).
(110% n) / 110% = 11 / 110%
n = 11 / 0.110
n = 100
So, the solution for n in the equation "110% n = 11" is n = 100.
B. The given equation is:
(328 x 128) x k = 328 x (82 x 128) x k
To solve for k, we can simplify the equation using the properties of multiplication.
Step 1: Perform the multiplications inside the parentheses:
41984 x k = 328 x 10576 x k
Step 2: Rearrange the equation by applying the associative property of multiplication:
41984 x k = 328 x (10576 x k)
Step 3: Divide both sides of the equation by 328:
(41984 x k) / 328 = 10576 x k
Step 4: Cancel out the common factor of k on the left-hand side:
(41984 / 328) x k = 10576 x k
Step 5: Simplify the left-hand side:
128 x k = 10576 x k
Step 6: Subtract 10576 x k from both sides of the equation to isolate k:
128 x k - 10576 x k = 0
Step 7: Factor out k on the left-hand side:
k x (128 - 10576) = 0
Step 8: Simplify further:
k x (-10448) = 0
Step 9: Divide both sides of the equation by (-10448):
k = 0
So, the solution for k in the equation "(328 x 128) x k = 328 x (82 x 128) x k" is k = 0.
At a local play production, 490 tickets were sold. The ticket prices varied on the seating arrangements and cost $8, $10, or $12. The total income from ticket sales reached $4600. If the combined number of $8 and $10 priced tickets sold was 6 times the number of $12 tickets sold, how many tickets of each type were sold?
Answers
PRICES COUNTS COSTS
8 e 8e
10 420-e-t 10(420-e-t)
12 t 12t
420 3920
system%28e%2B420-e-t=5t%2C8e%2B10%28420-e-t%29%2B12t=3920%29
First equation gives highlight%28t=70%29.
Second equation simplifies to e-t=140.
Substitution gives highlight%28e=210%29.
Quantity of $10 tickets by difference, highlight%28140%29
The perimeter of a rectangular garden is 332 m. If the width of the garden is 74 m, what is its length?
Answers
Solve -4(x + 1) - 3 = -3(x - 4).
1.-19
2.19
3.2
4.0
Answers
Answer:
(1) x=-19
Step-by-step explanation:
Let's solve your equation step-by-step.
−4(x+1)−3=−3(x−4)
Consider the following figures. Determine the direction of the current in the current-carrying wire that produces the field indicated in the figure. (a) * * * * * * * * * * * Bin * O out of the screen O into the screen O toward the left toward the right toward the top of the screen toward the bottom of the screen (b) O out of the screen O into the screen O toward the left toward the right O toward the top of the screen toward the bottom of the screen (C) * * * * O out of the screen into the screen lower right to upper left lower left to upper right upper right to lower left upper left to lower right
Answers
The direction of the current in the current-carrying wire that produces the field indicated in the figure is given below.
Conventionally, a positive charge would go in the same direction as an electric current. As a result, the battery's positive terminal receives less current in the external circuit than its negative counterpart. Indeed, electrons would go in the reverse direction across the cables.
According to Fleming's right-hand rule gives which direction the current flows. The right hand is held with thumb, index finger & middle finger mutually perpendicular to each other. The thumb is pointed in direction of motion to magnetic field of conductor relative to magnetic field.
(A) from right hand rule direction of current is towards left.
(B) Out of the Screen.
(C) Lower left to upper right.
According to Fleming's Right Hand Rule, if the thumb, forefinger, and middle finger are arranged in a straight line on the right hand, the thumb will point in the direction of the conductor's motion in relation to the magnetic field, the forefinger will point in the direction of the magnetic field, and the middle finger will point in the direction of the induced current.
Learn more about direction of the current :
https://brainly.com/question/15912115
#SPJ4



Find angles m<1 and m<2

Answers
Answer:
Step-by-step explanation:Angles 1 and 2 form a linear pair and are supplementary. So to find m∠2, subtract m∠1 from 180o. m∠2 = 180o - 135o = 45o.
...
Solution
m∠1 + 32 = 90 Substitute 32 for m∠2.
m∠1 = 58 Subtract 32 from each side.
m∠1 + m∠ 2 = 90 Definition of complementary angles.
Find the slope of the line through each pair of points.
(16,-11), (7,0)
Answers
Answer:
\(m=\frac{-11}{9}\)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Slope Formula: \(m=\frac{y_2-y_1}{x_2-x_1}\)Step-by-step explanation:
Step 1: Define
Point (16, -11)
Point (7, 0)
Step 2: Find slope m
Simply plug in the 2 coordinates into the slope formula to find slope m
Substitute [SF]: \(m=\frac{0+11}{7-16}\)Add/Subtract: \(m=\frac{11}{-9}\)Rewrite: \(m=\frac{-11}{9}\)The base of a solid is bounded by y=x,y=0, and x=1. Find the volume of the solid for each of the following cross sections (taken perpendicular to the y-axis): (a) squares, (b) semicircles, (c) equilateral triangles, and (d) semi ellipses whose heights are twice the lengths of their bases.
Answers
To find the volume of the solid, you need to calculate the area of each cross-section and then multiply that by the thickness of the section (which is the distance along the y-axis).
(a) Squares: The cross-sections are squares with sides of length y. The area of a square is side^2, so the area of each square is y^2. The thickness of the section is the distance along the y-axis, which is the difference between y and 0, or simply y. So the volume of the solid for each of the square cross-sections is y^2 * y
(b) Semicircles: The cross-sections are semicircles with radii of length y. The area of a semicircle is (pi * r^2) / 2 , so the area of each semicircle is (pi * y^2) / 2. The thickness of the section is the distance along the y-axis, which is the difference between y and 0, or simply y. So the volume of the solid for each of the semicircular cross-sections is (pi * y^2) / 2 * y
(c) Equilateral triangles: The cross-sections are equilateral triangles with side length of y. The area of an equilateral triangle is (s^2 * √3)/4. so the area of each equilateral triangle is (y^2 * √3) / 4. The thickness of the section is the distance along the y-axis, which is the difference between y and 0, or simply y. So the volume of the solid for each of the equilateral triangle cross-sections is (y^2 * √3) / 4 * y
(d) Semi-ellipses: The cross-sections are semi-ellipses whose heights are twice the lengths of their bases. The area of a semi-ellipse is πab/2, where a and b are the lengths of the semi-major and semi-minor axes respectively. Therefore the area of each semi-ellipse will be (πy^2)/2. The thickness of the section is the distance along the y-axis, which is the difference between y and 0, or simply y. So the volume of the solid for each of the semi-ellipse cross-sections is (πy^3)/2
It is important to note that this is a theoretical volume calculation, as the shape of the solid does not have a closed form representation by these functions, but rather, these are an approximation.
Also, for any of these volumes to be meaningful, we have to integrate over the range of the variable y, since it is bounded by the equations y=x, y=0 and x=1, the variable y is limited.
To know more about volume of the solid refer to:
brainly.com/question/21036176
#SPJ4
Which of the following is the value of sine Superscript negative 1 Baseline (StartFraction StartRoot 2 EndRoot Over 2 EndFraction)?
Answers
The value of sine Superscript negative 1 Baseline (StartFraction StartRoot 2 EndRoot Over 2 EndFraction) is π/4 radians or 45 degrees.
The value of sine Superscript negative 1 Baseline (StartFraction StartRoot 2 EndRoot Over 2 EndFraction) is π/4 radians or 45 degrees.What is inverse sine?
The inverse sine function or arc sine function is the inverse function of the sine function. It is defined as follows:If y = sin x, then x = sin-1 y, where x is the angle whose sine is y.
The range of the inverse sine function is from -π/2 to π/2 radians or from -90 to 90 degrees. It is denoted by sin-1 or arcsin.What is the value of sine Superscript negative 1 Baseline (StartFraction StartRoot 2 EndRoot Over 2 EndFraction)?
Given that the value of sine Superscript negative 1 Baseline (StartFraction StartRoot 2 EndRoot Over 2 EndFraction) is to be determined.
Using the formula, sin θ = opposite side/hypotenuse= (StartRoot 2) / 2= 0.707The angle whose sine is 0.707 can be found using a calculator or a unit circle.
The inverse sine of 0.707 is π/4 radians or 45 degrees.
To learn more about : value
https://brainly.com/question/843074
#SPJ8
It is claimed that 55% of marriages in the state of California end in divorce within the first 15 years. A large study was started 15 years ago and has been tracking hundreds of marriages in the state of California. Suppose 10 marriages are randomly selected. What is the probability that less than two of them ended in a divorce
Answers
Answer:
0.0045 = 0.45% probability that less than two of them ended in a divorce
Step-by-step explanation:
For each marriage, there are only two possible outcomes. Either it ended in divorce, or it did not. The probability of a marriage ending in divorce is independent of any other marriage. This means that the binomial probability distribution is used to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
In which \(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
And p is the probability of X happening.
55% of marriages in the state of California end in divorce within the first 15 years.
This means that \(p = 0.55\)
Suppose 10 marriages are randomly selected.
This means that \(n = 10\)
What is the probability that less than two of them ended in a divorce?
This is
\(P(X < 2) = P(X = 0) + P(X = 1)\)
In which
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 0) = C_{10,0}.(0.55)^{0}.(0.45)^{10} = 0.0003\)
\(P(X = 1) = C_{10,1}.(0.55)^{1}.(0.45)^{9} = 0.0042\)
\(P(X < 2) = P(X = 0) + P(X = 1) = 0.0003 + 0.0042 = 0.0045\)
0.0045 = 0.45% probability that less than two of them ended in a divorce
Please help! 5th grade math!

Answers
Answer:
Option C
Step-by-step explanation:
Answer:
C
Step-by-step explanation:
It has 2 lines that mirror each other and they never touch no matter how long it is.
What is the formula forfinding the area of a circle using its radius or diameter.
Answers
Answer:
The formula for finding the area of a circle using its radius is:
The formula for finding the area of a circle using its radius is:A = πr²
The formula for finding the area of a circle using its radius is:A = πr²where A is the area of the circle and r is its radius.
The formula for finding the area of a circle using its radius is:A = πr²where A is the area of the circle and r is its radius.The formula for finding the area of a circle using its diameter is:
The formula for finding the area of a circle using its radius is:A = πr²where A is the area of the circle and r is its radius.The formula for finding the area of a circle using its diameter is:A = (π/4)d²
The formula for finding the area of a circle using its radius is:A = πr²where A is the area of the circle and r is its radius.The formula for finding the area of a circle using its diameter is:A = (π/4)d²where A is the area of the circle and d is its diameter.
The formula for finding the area of a circle using its radius is:A = πr²where A is the area of the circle and r is its radius.The formula for finding the area of a circle using its diameter is:A = (π/4)d²where A is the area of the circle and d is its diameter.Note that π (pi) is a mathematical constant that represents the ratio of the circumference of a circle to its diameter and is approximately equal to 3.14
Step-by-step explanation:
Hope it Helps
The formula for finding the area of a circle using its radius is π * r².
The formula for finding the area of a circle using its diameter is (π/4) * d².
The formula for finding the area of a circle using its radius is:
A = π * r²
where:
A represents the area of the circle,
π (pi) is a mathematical constant approximately equal to 3.14159, and
r represents the radius of the circle.
If you have the diameter of the circle instead of the radius, you can use the following formula:
A = (π/4) * d²
where:
A represents the area of the circle,
π (pi) is a mathematical constant approximately equal to 3.14159, and
d is the diameter of the circle.
For more information on the Area of Circle, click:
https://brainly.com/question/14068861
Which of the expressions are equivalent to the one below check all the apply (12 + 3) ÷ 5

Answers
The expression is equivalent to the expression (12 + 3) ÷ 5 is (3 + 12) ÷ 5
Which of the expressions are equivalent to the expressionFrom the question, we have the following parameters that can be used in our computation:
(12 + 3) ÷ 5
The above expression is a quotient expression
However, we can apply some algebraic properties
Take for instance;
12 + 3 can be expressed as 3 + 12
So, we have
(12 + 3) ÷ 5 = (3 + 12) ÷ 5
Hence, the expression is equivalent to the expression is (3 + 12) ÷ 5
Read more about expression at
https://brainly.com/question/15775046
#SPJ1
Billy took 5 tests in his math class. He scored an 89,88,93,90 and 81. What is the variance of his grades in these test? If necessary, round to the nearest hundredth.
Answers
The variance of Billy's grades obtained from his test scores is 15.76
What is variance?The variance is a measure of variability or spread a dataset. The variance can be calculated from the sum of the square of the differences of the data points from the mean divided by the number or count of the data points.
The variance of Billy's test scores can be calculated by finding the mean or the average of the scores, then finding the sum of the squares of the differences of each score from the mean as follows;
The mean score = (89 + 88 + 93 + 90 + 81)/5 = 88.2
The square of the differences of the values from the mean can be calculated as follows;
(89 - 88.2)² = 0.64, (88 - 88.2)² = 0.04, (93 - 88.2)² = 23.04, (90 - 88.2)² = 3.24, and (81 - 88.2)² = 51.84
The sum of the square of the differences is therefore;
0.64 + 0.04 + 23.04 + 3.24 + 51.84 = 78.8
The variance is therefore; 78.8/5 = 15.76Learn more on the variance of a set of data here: https://brainly.com/question/30701163
#SPJ1
find the indicated limit if it exists

Answers
Answer:
\(\displaystyle \lim_{x \to \infty} \frac{x^2}{1 + 3x + 5x^2} = \frac{1}{5}\)
General Formulas and Concepts:
Calculus
LimitsStep-by-step explanation:
Step 1: Define
\(\displaystyle \lim_{x \to \infty} \frac{x^2}{1 + 3x + 5x^2}\)
Step 2: Determine Rule
If the highest power of x in a rational expression is the same both numerator and denominator, then the limit as x approached ∞ would be the highest term coefficient in the numerator divided by the highest term coefficient in the denominator.
Step 3: Identify
Numerator highest power: x²
Coefficient: 1Denominator highest power: 5x²
Coefficient: 5Step 4: Evaluate
Apply rule.
\(\displaystyle \lim_{x \to \infty} \frac{x^2}{1 + 3x + 5x^2} = \frac{1}{5}\)
Topic: AP Calculus AB/BC (Calculus I/II)
Unit: Limits
Book: College Calculus 10e
10. Higher Order Thinking Each of 5 friends has x action figures in
his or her collection. Each friend buys 11 more action figures. Now
the 5 friends have a total of 120 action figures.
a. Write an equation that models the problem.
b. Solve the equation to find the number of action figures, x, that
each friend had originally.
Answers
Each friend had originally 13 action figures before buying 11 more.
Given that there are 5 friends and each of them has x action figures in his or her collection. When they buy 11 more action figures, the total number of action figures they will have is 120.
a) We need to find an equation that models the problem. Let x be the original number of action figures that each friend had.
Therefore, the total number of action figures that each friend will have after purchasing 11 more is x + 11.
The total number of action figures will be 5(x + 11) = 5x + 55.
Now, according to the problem,5x + 55 = 120
This is our equation that models the problem.
b) We have to solve the equation 5x + 55 = 120 to find the original number of action figures, x, that each friend had before buying 11 more action figures.
5x + 55 = 120
5x = 120 - 55 (subtract 55 from both sides)
5x = 65x = 13
Therefore, each friend had originally 13 action figures before buying 11 more.
For more such questions on figures, click on:
https://brainly.com/question/24491627
#SPJ8
which value of x makes this inequality true? x+9<4x
Answers
Answer:
Step-by-step explanation:
x+9
Let x, be 4
4+9=13
given condition,
x+9<4x
4+9<4(4)
13<16
The answer is:
x > 3Work/explanation:
Our inequality is:
\(\sf{x+9 < 4x}\)
Flip it
\(\sf{4x > x+9}\)
Solve
\(\sf{4x-x > 9}\)
Combine like terms
\(\sf{3x > 9}\)
Divide each side by 3
\(\sf{x > 3}\)
Hence, x > 3If u steal point i report

Answers
Answer:
The first option
Step-by-step explanation:
Refer to the figure below.
BED and CEA are
angles.
A
C
E
D
B
Answers
Answer:
both two
Step-by-step explanation:
because it is in alphabetical order
writie any assay about challenges of teaching mathematics on 21st century
Answers
Unit 9 lesson1 7th grade math math nation
Answers
find the value of x.
please help! :)

Answers
Answer:
x=9
Step-by-step explanation:
Mr. House wrote 8 tenths minus 5 hundredths on the board. Maggie said the answer is 3 hundredths
because 8 minus 5 is 3. 5 Is she correct? Explain.
Answers
0.8 is 8 tenths minus
0.05
Which would basically be
0.80-
0.05 which is
0.75
What is the m∠J, to the nearest tenth? JLK is right angle triangle. The length of JL is 9.4 and length of LK is 15.1. explaination?
Answers
The angle m∠J in the right angle triangle is 58.1 degrees.
How to find the angle of a triangle?One of the angle of a right tangle triangle is 90 degrees. The sum of
angles in a triangle is 180 degrees.
Therefore, the side length LK can be found using Pythagoras's theorem and the angle can be found using trigonometric ratios.
Hence,
tan ∠J = opposite / adjacent
tan ∠J = 15.1 / 9.4
∠J = tan⁻¹ 1.60638297872
∠J = 58.0909229196
Therefore,
m∠J = 58.1 degrees
learn more on right triangle here: https://brainly.com/question/22626760
#SPJ1
Solve the equation: x²-2x=8
Show all the Steps with explanation.
Answers
Answer:
x = 4, -2
Step-by-step explanation:
x^2-2x=8
Move the constant term to the right side of the equation.
x^2 - 2x = 8
Take half of the coefficient of x and square it.
(-2/2)^2 = 1
Add the square to both sides of the equation.
x^2 - 2x + 1 = 8 + 1
Factor the perfect square trinomial.
(x - 1)^2 = 9
Take the square root of both sides of the equation.
x-1=\(\sqrt{9}\)
x-1=±3
Isolate x to find the solutions.
Taking positive
x=3+1=4
x=4
Taking negative
x=-3+1
x=-2
The solutions are:
x = 4, -2
Answer:
\(x = -2,\;\;x=4\)
Step-by-step explanation:
To solve the quadratic equation x² - 2x = 8 by factoring, subtract 8 from both sides of the equation so that it is in the form ax² + bx + c = 0:
\(x^2-2x-8=8-8\)
\(x^2-2x-8=0\)
Find two numbers whose product is equal to the product of the coefficient of the x²-term and the constant term, and whose sum is equal to the coefficient of the x-term.
The two numbers whose product is -8 and sum is -2 are -4 and 2.
Rewrite the coefficient of the middle term as the sum of these two numbers:
\(x^2-4x+2x-8=0\)
Factor the first two terms and the last two terms separately:
\(x(x-4)+2(x-4)=0\)
Factor out the common term (x - 4):
\((x+2)(x-4)=0\)
Apply the zero-product property:
\(x+2=0 \implies x=-2\)
\(x-4=0 \implies x=4\)
Therefore, the solutions to the given quadratic equation are:
\(\boxed{x = -2,\;\;x=4}\)
Select the correct answer. If is modified as , what transformations will be seen in the graph? A. The graph will reflect across the x-axis and then shift units up. B. The graph will reflect across the y-axis and then shift units down. C. The graph will reflect across the x-axis and then shift units to left. D. The graph will reflect across the y-axis and then shift units to right.
Answers
The transformation is (b) The graph will reflect across the y-axis and then shift 5 units down.
How to determine the transformation?The missing phrase in the question is: "If f(x) = 2ˣ + 1 is modified as g(x) = 2⁻ˣ + 1 - 5"
The functions are given as:
f(x) = 2ˣ + 1
g(x) = 2⁻ˣ + 1 - 5
First, the function f(x) is reflected across the y-axis (this eliminates options a and c)
The rule of this transformation is
(x,y) ⇒ (-x,y)
So, we have:
f'(x) = 2⁻ˣ + 1
Next, the function f(x) is shifted down by 5 units (this eliminates options d)
The rule of this transformation is
(x,y) ⇒ (x,y - 5)
So, we have:
f''(x) = 2⁻ˣ + 1 - 5
By comparing the functions f"(x) and g(x), we have:
g(x) = f''(x) = 2⁻ˣ + 1 - 5
Hence, the transformation is (b) The graph will reflect across the y-axis and then shift 5 units down.
Read more about transformation at:
https://brainly.com/question/4289712
#SPJ1
video
Let the region R be the area enclosed by the function f(x) = ln (x) + 1 and
g(x)=x-1. If the region R is the base of a solid such that each cross section
perpendicular to the a-axis is a semi-circle with diameters extending through the
region R, find the volume of the solid. You may use a calculator and round to the
nearest thousandth.

Answers
The volume of the solid is approximately 0.558 cubic units.
To find the volume of the solid, we need to integrate the area of the semi-circles along the a-axis.
We know that the diameter of each semi-circle is the distance between the functions f(x) and g(x), which is:
d(a) = f(a) - g(a) = ln(a) + 1 - (a-1) = ln(a) - a + 2
The radius of each semi-circle is half of the diameter, which is:
r(a) = (ln(a) - a + 2) / 2
The area of each semi-circle is π times the square of its radius, which is:
\(A(a) = πr(a)^2 = π/4 (ln(a) - a + 2)^2\)
To find the volume of the solid, we integrate the area of each semi-circle along the a-axis, from a = e to a = 2:
V = ∫[e,2] A(a) da
V = ∫[e,2] π/4 \((ln(a) - a + 2)^2 da\)
V ≈ 0.558 (rounded to the nearest thousandth)
Therefore, the volume of the solid is approximately 0.558 cubic units.
for such more question on volume
https://brainly.com/question/6204273
#SPJ11
help pleaseeeeeeeeeeee

Answers
Answer: Roger should pick Printer B because it prints 2 more pages per minute.
Step-by-step explanation: We are given that printer A prints 33 pages per minute. We have to figure out how many pages printer B prints in a minute.
As shown in the table, in 2 minutes, printer B prints 70 pages, and in 3 minutes it prints 105 pages. We can create a function to model the rate at which printer A prints pages. This is a linear function since for each increase in x, there is a proportional increase in y. This means that if we were to back one minute the printer would print 35 pages since the common difference per minute is 35 pages. The function would therefore be p=35m where m=minutes and p=pages. This means that printer B produces 2 more pages than printer A per minute since 33+2=35.
for what value of a is x-3 a factor of x^3-4x^2+ax-2a
Answers
Answer:
2x
Step-by-step explanation:
because it's2 so two ok carRy on
The value of a is 9.
What is factor?
A factor of polynomial P(x) is any polynomial which divides evenly into P(x).
How to find the solution for a polynomial?For finding the factor of a polynomial we will perform following steps:
If f(x) is any polynomial then substitute f(x) = 0.Then factorize the given polynomial by splitting the middle term. Then solve for x.According to the given question.
We have a cubic polynomial \(x^{3} -4x^{2} +ax -2a\)
Also, x - 3a is a factor of the given polynomial.
⇒ \(x - 3 = 0\)
⇒\(x = 3\)
⇒ 3 is the one solution of the given cubic polynomial.
If 3 is the one solution of the cubic polynomial then it must satisfy the equation (i).
So, substitute the value of x in the given polynomial.
\((3)^{3} -4(3)^{2} + a (3) - 2a = 0\)
⇒\(27 -4(3)^{2} +a(3) -2a=0\)
⇒\(27 - 36 + 3a - 2a= 0\)
⇒\(-9 + a = 0\)
⇒ \(a = 9\)
Therefore, the value of a is 9.
Find out more information about factor and solution of polynomial here:
https://brainly.com/question/26354419
#SPJ2