3x+3(x+y) please help
Answers
Answer:
6x + 3y
Step-by-step explanation:
distribute
3x + 3x + 3y
Combine like terms
6x + 3y
theres ur answer
Related Questions
Solve 3(x + 2) >x
Please
Answers
Answer:
x > −3
Step-by-step explanation:
Let's solve your inequality step-by-step.
3(x + 2) > x
Step 1: Simplify both sides of the inequality.
3x + 6 > x
Step 2: Subtract x from both sides.
3x + 6 − x > x − x
2x + 6 > 0
Step 3: Subtract 6 from both sides.
2x + 6 − 6 > 0 − 6
2x > −6
Step 4: Divide both sides by 2.
2x / 2 > −6 / 2
x > −3
Answer:
x > −3
Hope this helps :)
if a triangle has two angles that measures 46 and 102 degrees, what is the measure of the third angle?
Answers
Answer:
All triangles need to have 180 degrees
subtract the angles you already know
180 - 102 - 46 = 180 - 148 = 32
There is 32 degrees left so 32 is the answer
Step-by-step explanation:
Answer:
32°
Step-by-step explanation:
The triangle sum theorem states that the measures of the angles of a triangle is 180°
a large software company gives job applicants a test of programming ability and the mean for that test has been 160 in the past. twenty-five job applicants are randomly selected from one large university and they produce a mean score and standard deviation of 183 and 12, respectively. use a 0.05 level og significance to test the claim that this sample comes from a population with a mean score greater than 160. use the P-value method of testing hypotheses.
Answers
Using the P-value method of testing hypotheses with a significance level of 0.05, the sample provides strong evidence to support the claim that the mean score of job applicants from the university is greater than 160.
To test the claim that the mean score of job applicants from the university is greater than 160, we will perform a one-sample t-test using the P-value method. The null hypothesis (H0) assumes that the mean score is equal to 160, while the alternative hypothesis (Ha) assumes that the mean score is greater than 160.
First, we calculate the test statistic, which is the t-value. The formula for the t-value is:
t = (sample mean - hypothesized mean) / (sample standard deviation / sqrt(sample size))
Plugging in the given values, we have:
t = (183 - 160) / (12 / √(25))
= 23 / (12 / 5)
= 23 * (5 / 12)
≈ 9.58
Next, we find the P-value associated with the test statistic. The P-value represents the probability of obtaining a test statistic as extreme as the observed value, assuming the null hypothesis is true. Since the alternative hypothesis is one-sided (greater than 160), we calculate the P-value by finding the probability of the t-distribution with 24 degrees of freedom being greater than the calculated t-value.
Consulting statistical tables or using software, we find that the P-value is very small (less than 0.0001).
Since the P-value (less than 0.0001) is less than the significance level (0.05), we reject the null hypothesis. This provides strong evidence to support the claim that the mean score of job applicants from the university is greater than 160.
Learn more about P-value
brainly.com/question/30461126
#SPJ11
to find p(0 ≤ z ≤ 1.37) using appendix c-1, find the row containing 0.1 in the far left column. then find the column containing .037 in the top row. (round the values to 2 decimal places.)
Answers
The value of p(0 ≤ z ≤ 1.37) is approximately 0.41 (rounded to 2 decimal places).
What is Probability ?
Probability is a branch of mathematics that deals with the study of the likelihood or chance of an event occurring. It is the measure of the likelihood that a particular event or set of events will occur.
To find the value of p(0 ≤ z ≤ 1.37) using Appendix C-1, we need to locate the row containing 0.1 in the far-left column and the column containing 0.37 in the top row.
Starting with the row containing 0.1 in the far-left column, we can locate the value closest to 1.3 in the row, which is 1.37. Moving along the row to the right, we can find the corresponding value of the cumulative distribution function (CDF) for this value of z, which is 0.9147.
Next, we need to find the column containing 0.37 in the top row. The closest value in the column is 0.3707. Moving down the column to the row containing the CDF value we just found, we can read off the value of the CDF for z = 0, which is 0.5000.
To find the value of p(0 ≤ z ≤ 1.37), we subtract the CDF value for z = 0 from the CDF value for z = 1.37:
p(0 ≤ z ≤ 1.37) = 0.9147 - 0.5000 = 0.4147
Therefore, the value of p(0 ≤ z ≤ 1.37) is approximately 0.41 (rounded to 2 decimal places).
To learn more about Probability from given link.
https://brainly.com/question/29221515
#SPJ1
A fair spinner has 12 equal sections: 3 red, 5 blue and 4 green.
It is spun twice.
What is the probability of getting not green then green?
Answers
Answer:
2/9 = approximately 0.22.
Step-by-step explanation:
There are a total of 12 possible outcomes when the spinner is spun once, so the probability of getting a result that is not green is 8/12, or 2/3. Similarly, the probability of getting green on the second spin is 4/12, or 1/3.
To find the probability of getting a result that is not green on the first spin and green on the second spin, you can multiply the probabilities of each individual event. Therefore, the probability of getting not green then green is (2/3) * (1/3) = 2/9 = approximately 0.22.
Alternatively, you could also use the principle of complementary probabilities to calculate the probability of getting not green on the first spin and green on the second spin. The probability of getting not green on the first spin is 1 - (4/12) = 8/12 = 2/3, and the probability of getting green on the second spin is still 4/12 = 1/3. Multiplying these probabilities gives a result of (2/3) * (1/3) = 2/9 = approximately 0.22.
In a set of three lines, a pair of parallel lines is intersected by a transversal. The intersection forms eight special angles.
Two of the special angles, A and B, are corresponding angles.
For the set of parallel lines intersected by a transversal, A = 4x and B = 2(x+14).
1. Use an equation to represent the corresponding angle relationship between A and B.
2. Use the equation to find the measures of A and B.
PLEASE HELP!!! Will mark brainliest and give thanks:)
Answers
Answer:
a.) 4x = 2(x + 14)
b.) Measure of A = 56°
Measure of B = 56°
Step-by-step explanation:
We know that,
When two lines are crossed by another line transversal line , the angles in matching corners are called corresponding angles.
Also,
When two lines are parallel then the Corresponding Angles are equal.
Given that,
A = 4x and B = 2(x+14).
i.e.
∠A = 4x and ∠B = 2(x+14)
a.)
Now,
As A and B are parallel
So,
∠A = ∠B
⇒4x = 2(x + 14)
(This is the equation that represent the corresponding angle relationship between A and B.)
b.)
Now,
⇒4x = 2x + 2(14)
⇒4x = 2x + 28
⇒4x - 2x = 28
⇒2x = 28
⇒x = 14
So,
we get
∠A = 4(14)
= 56
⇒∠A = 56°
and
∠B = 2(14 + 14)
= 2(28)
= 56°
⇒∠B = 56°
∴ we get
Measure of A = 56°
Measure of B = 56°
a biotechnology company produces a therapeutic drug whose concentration has a standard deviation of 4 g/l. a new method of producing this drug has been proposed, although some additional cost is involved. management will authorize a change in production technique only if the standard deviation of the concentration in the new process is less than 4 g/l. the researchers chose n 10 and obtained the following data. perform the necessary analysis to determine whether a change in production technique should be implemented. 16.628 g/l 16.630 g/l 16.622 16.631 16.627 16.624 16.623 16.622 16.618 16.626
Answers
After answering the provided question, we can conclude that t = 1.833 is standard deviation the critical value for a one-tailed t-test with 9 degrees of freedom and a significance level of 0.05.
What is standard deviation?A statistic that communicates the fluctuation or variance of a number set is the standard deviation. A high standard deviation indicates that the values seem to be more dispersed, whereas a low standard deviation indicates that the values are closer to the established mean. The standard deviation is a measure of how far the data varies from the mean (or ). So when standard deviation is small, the data tends to cluster around the mean; when it is huge, the data is more dispersed. The standard deviation represents the average variability of something like the data set. It displays the average deviation from the mean of each score.
To decide whether the new manufacturing technique should be used, we must first determine whether the standard deviation of the drug concentration in the new process is less than 4 g/l. A hypothesis test can be used with the following null and alternative hypotheses:
H0 (null hypothesis): In the new process, the standard deviation of drug concentration is 4 g/l.
Alternative hypothesis (Ha): In the new process, the standard deviation of drug concentration is less than 4 g/l.
For the standard deviation, we can use a one-tailed t-test with a
\(t = (n - 1) * s^2 / \sigma^2\\s = \sqrt(1/(n-1) * \sum(xi - x\bar)^2) = 0.004 g/l\\t = (n - 1) * s^2 / \sigma^2 = (10 - 1) * 0.004^2 / 4^2 = 0.0007\)
t = 1.833 is the critical value for a one-tailed t-test with 9 degrees of freedom and a significance level of 0.05.
To know more about standard deviation visit:
https://brainly.com/question/23907081
#SPJ1
PLEASE HELP!!!
The population of a town increases by 3% each year. If its population today is 25,000, what will its population be in 5 years?
A 25,000 (1.03)
B 25,000-(1.03)5
25,000-(0.03)
25,000 (1.03) - (5)
Answers
The population of the town in 5 years will be approximately 28,982.
What is exponential growth?A data pattern known as exponential growth exhibits faster expansion over time. Compounding generates exponential profits in finance. Exponential growth is possible in savings accounts with a compounding interest rate. Compound returns in finance lead to exponential development. One of the most potent forces in finance is the power of compounding. With the help of this idea, investors may generate sizable sums with little start-up money. Compound interest savings accounts are typical instances of exponential development.
Given that, population of a town increases by 3% each year.
The population after 5 years is calculated by:
Population in 5 years = Initial population x (1 + rate) raised to time.
That is,
Population in 5 years = 25,000 x (1 + 0.03)⁵
Population in 5 years = 25,000 x 1.159274
Population in 5 years = 28,981.85
Hence, the population of the town in 5 years will be approximately 28,982.
Learn more about exponential growth here:
https://brainly.com/question/11487261
#SPJ1
The lengths of two similar figures are 32 ft and 36 ft. What is the scale factor, perimeter ratio and area ratio in simplest form of the first to the second.
Answers
Scale factor from the first to the second figure is 9/8, Perimeter ratio is 37/32 and the area ratio of the first to the second figure is 81/64 in simplest form.
Since the figures are similar, their corresponding sides are proportional. Let the scale factor between the two figures be x, then we have:
x = (length of the second figure) / (length of the first figure)
= 36/32 = 9/8
So the scale factor from the first to the second figure is 9/8.
Perimeter ratio = (perimeter of the second figure) / (perimeter of the first figure)
Perimeter ratio = (9/8) × [(36 + 32) / 2] / 32 = 37/32
Since the area of a figure is proportional to the square of its sides, and the sides are proportional by the scale factor
The area of the second figure is (9/8)² times the area of the first figure.
Area ratio = (area of the second figure) / (area of the first figure)
= [(9/8)² × (area of the first figure)] / (area of the first figure)
Area ratio = 81/64
Hence, scale factor from the first to the second figure is 9/8, Perimeter ratio is 37/32 and the area ratio of the first to the second figure is 81/64 in simplest form.
To learn more on Ratios click:
https://brainly.com/question/1504221
#SPJ1
A cyclist travels 18 miles in 45 minutes.
What is his average speed in mph?
Answers
Answer:
Divide the total distance traveled by the total time spent traveling. This will give you your average speed
Step-by-step explanation:
No Explanation Needed Just Common Sense , And A CALCULATOR!
the town of abridge currently has a population of 300,000 each year the population will reduce by 7% how many fewer people will live in abridge in 5 years compared with now give your answer to 3 sf
Answers
Answer:
91,300 to 3 s.f.
Step-by-step explanation:
The population is reduced by a percentage 100-7 = 93% ( or 0.93) per year.
So after 5 years thatwould be 300,000(0.93)^5
= 208707
that is 300,000 - 208,706
= 91293
= 91,300 to 3 s.f.
If K < 1 , Δ G is: a. zero b. negative c. one d. positive
Answers
If the equilibrium constant (K) < 1 , then, the Gibbs free energy change(ΔG) is positive. So, option D is correct alternative.
The relative concentrations of reactants and products in a chemical reaction are gauged by the equilibrium constant (K), which is the case in this case. Typical chemical reactions are as follows:
aA + bB ⇌ cC + dD
The equilibrium constant is defined as:
\(K = \frac{[C]^c[D]^d }{ [A]^a[B]^b}\)
Where [A], [B], [C], and [D] are the molar concentrations of reactants and products at equilibrium, and a, b, c, and d are the stoichiometric coefficients of the balanced chemical equation.
The Gibbs free energy change (ΔG) is a measure of the amount of energy available to do useful work during a chemical reaction.
The following equation describes the relationship between the equilibrium constant (K) and the change in the Gibbs free energy (ΔG):
ΔG = -RTln(K)
Where R is the gas constant and T is the temperature.
If K < 1, then ln(K) is negative. So, to make the right-hand side of the equation negative, ΔG must be positive.
To know extra about Gibbs free energy
brainly.com/question/13318988
#SPJ4
PLEASE HELP ME THIS IS URGENT
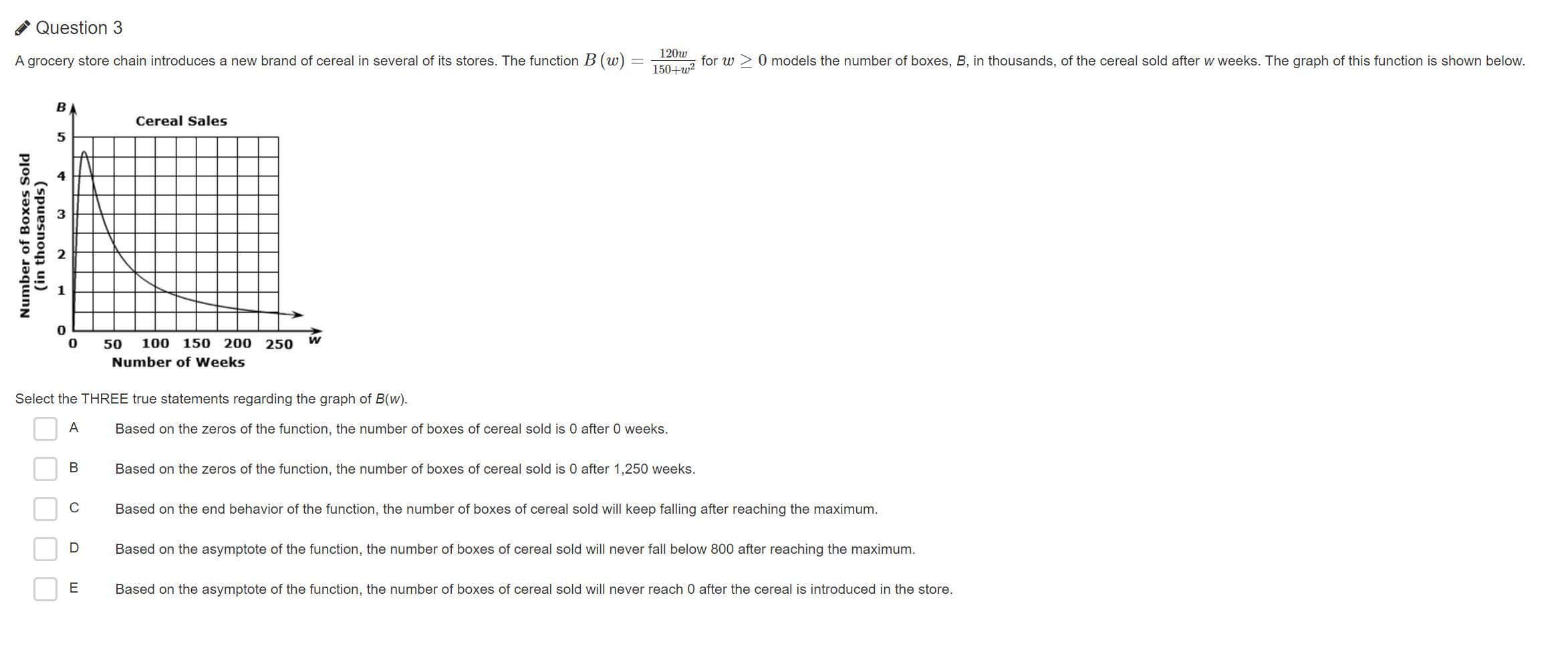
Answers
Using the concept of asymptote of the function it can be concluded that the number of boxes of cereals sold is 0 after 0 weeks, it will keep falling after reaching the maximum sales and cereals sold is always positive as the cereals introduced so the correct option are A, C and E.
What is the asymptote of the function?A line that a curve approaches but never touches is an asymptote. The graph of a function converges to a line known as an asymptote, in other words. When graphing functions, asymptotes are usually not necessary to be drawn. The curve must not contact the asymptote when we graph them using dotted lines (imaginary lines). As a result, the asymptotes are merely made-up lines. When either the value of x or y tends to or -, the distance between the asymptote of a function, y = f(x), and its graph is close to zero.
Option A is correct as according to the option A: - B(w)= \(\frac{120w}{150+w^{2} }\), w=0.
On putting the value of w=0 in above function implies B(w)=0.
Hence, number of boxes of cereals sold is 0 after 0 weeks.
Option C is correct as function B(w) is decreasing function after reaching its maxima according to graph.
Option E is correct as B(w)= \(\frac{120w}{150+w^{2} }\), if w>0
implies that B(w)>0 as numerator>0 and denominator>0.
Based on the asymptote of function the number of boxes of cereals never reach 0 after cereals introduced in the store.
To know more about asymptote of function, visit:
https://brainly.com/question/28213818
#SPJ1
FILL THE BLANK. variabe number tandem repeat (vntr) analysis involves ________.
Answers
VNTR analysis involves examining and analyzing the variations in the number of repeated DNA sequences known as tandem repeats.
VARIABLE NUMBER TANDEM REPEAT (VNTR) analysis involves examining and analyzing the variations in the number of repeated DNA sequences known as tandem repeats.
These tandem repeats consist of short DNA sequences repeated in a head-to-tail fashion.
VNTR analysis primarily focuses on identifying and characterizing the variations in the number of repeats within specific genomic regions.
By studying VNTRs, scientists can gain insights into genetic diversity, individual identification, and genetic relationships among individuals or populations.
VNTR analysis typically involves techniques such as polymerase chain reaction (PCR) amplification of the target region, followed by fragment analysis to determine the number of repeats present.
The variations in VNTRs make them highly polymorphic, meaning they differ significantly between individuals.
This polymorphism allows VNTR analysis to be used in various applications, including forensic analysis, paternity testing, population genetics, and evolutionary studies.
In summary, VNTR analysis involves examining and analyzing the variations in the number of repeated DNA sequences known as tandem repeats, providing valuable information for genetic diversity and identification purposes.
Learn more about DNA here:
https://brainly.com/question/30396067
#SPJ11
I really need help..im confused

Answers
The coefficient of determination, also known as R-squared, represents the proportion of the dependent variable's variance that can be explained by the independent variable(s) in a regression model. A higher R-squared indicates a better fit of the model to the data and suggests that a greater proportion of the variation in the dependent variable (lobster length in this case) can be attributed to the independent variable (age).
In this scenario, the linear model has a coefficient of determination of 0.8724503, indicating that approximately 87% of the variation in lobster length can be explained by age. This suggests a strong relationship between age and length in a linear fashion.
Conversely, the exponential model has a lower coefficient of determination of 0.6730372, indicating that only about 67% of the variation in lobster length is associated with age. While this is still a moderate level of association, the linear model provides a better fit to the data and explains a higher proportion of the variation in length.
Therefore, based on the coefficient of determination, the linear model would be the better choice for projecting the length of a lobster.
what's the answer to r over 9 =-4
Answers
Answer:
r = -36
Step-by-step explanation:
\(\frac{r}{9}=-4\)
Multiply both sides by 9
r = -36
653005 number with commas as per the international number system
Answers
Answer:
653005 = 653,005 in the International System of Numeration, the number is (Six hundred fifty-three thousand and five)
How many fish are in the aquarium in the restaurant?
Answers
Answer:
Which Restaurant and aquarium
Step-by-step explanation:
If you tell the name I can answer it
Given a hashing function H(x) = y, where y is an n=128 bit output:
1. find the number of computations(hashes) required for finding a collision at 80% and 10% probabilities. Provide figures with 4 decimals.
2. you’ve access to a computer that can process a trillion hashes per second, how long will it take to find a collision at 10% probability?
Answers
1. The number of computations (hashes) required for finding a collision at 80% and 10% probabilities is 1.8447 x 10^19.
2. It will take approximately 47,891 seconds (or 13.3 hours) to find a collision at 10% probability.
The number of computations (hashes) required for finding a collision at 80% and 10% probabilities depends on the size of the hash function output. Let's assume a hash function output size of 128 bits for this example.
For finding a collision at 80% probability, we need to use the birthday attack algorithm. The number of hashes required can be calculated using the following formula:
N = sqrt((2^(n+1))*ln(1/(1-p)))
where n is the size of the hash output in bits (n=128 in this case), p is the desired probability of finding a collision (p=0.8 in this case), ln is the natural logarithm, and sqrt is the square root function.
Substituting the values, we get:
N = sqrt((2^(128+1))*ln(1/(1-0.8))) = 2^64.3155 = 1.8447 x 10^19
Therefore, we need 1.8447 x 10^19 hashes to find a collision at 80% probability.
For finding a collision at 10% probability, we can use the following formula:
N = sqrt((2^(n+1))*ln(1/(1-p)))
Substituting the values, we get:
N = sqrt((2^(128+1))*ln(1/(1-0.1))) = 2^55.9724 = 4.7891 x 10^16
Therefore, we need 4.7891 x 10^16 hashes to find a collision at 10% probability.
If we have a computer that can process a trillion hashes per second, we can calculate the time required to find a collision at 10% probability as follows:
time = N / rate
where N is the number of hashes required to find a collision (N=4.7891 x 10^16), and rate is the rate of hashes that the computer can process per second (rate=1 trillion = 1 x 10^12).
Substituting the values, we get:
time = (4.7891 x 10^16) / (1 x 10^12) = 4.7891 x 10^4 seconds
Therefore, it will take approximately 47,891 seconds (or 13.3 hours) to find a collision at 10% probability with a computer that can process a trillion hashes per second.
Know more about computations here:
https://brainly.com/question/29558206
#SPJ11
a lamp manufacturer has developed five lamp bases and four lampshades that could be used together. how many different arrangements of base and shade can be offered? a. 5 b. 10 c. 15 d. 20
Answers
Different lampshades that could be used together are A) 5.
How to determine the value of any factorial value?
The factorial function (symbol:!) instructs us to multiply all whole numbers starting at the number we have chosen down to one.
Examples:
4! = 4 × 3 × 2 × 1 = 24
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
according to the question, five lamp bases and four lampshades that could be used together. so the calculation will be 5C4
using factorial,
Hence, 5 different arrangements of base and shade can be offered together. (using factorial)
to learn more about factorial from the given link,
https://brainly.com/question/25997932
#SPJ4
1.
a.) Determine the truth sets of the following propositions over the positive integers:
p ( n ) : n is a perfect square and n < 100
q ( n ) : n = | P ( A ) | for some set A .
b.) DetermineT_{p\wedge q}for p and q above.
Answers
a) To determine the truth sets of p(n) and q(n), we need to determine the set of positive integers for which each proposition is true.
For p(n), we are looking for positive integers that are perfect squares and less than 100. These integers are:
1, 4, 9, 16, 25, 36, 49, 64, 81
So the truth set of p(n) is {1, 4, 9, 16, 25, 36, 49, 64, 81}.
For q(n), we are looking for positive integers that are equal to the cardinality of some set A. Since the cardinality of a set A can only be a non-negative integer, the truth set of q(n) is the set of all non-negative integers.
b) To determine T(p ∧ q), we need to find the set of positive integers that satisfy both p(n) and q(n).
the set of positive integers that satisfy both p(n) and q(n) is {1, 4, 9, 16, 25, 36, 49, 64, 81}.
From part a), we know that the truth set of p(n) is {1, 4, 9, 16, 25, 36, 49, 64, 81}. For a positive integer n to satisfy both p(n) and q(n), it must be the case that n = |P(A)| for some set A and that n is also a perfect square less than 100.
We can start by considering the smallest perfect square less than 100, which is 1. Since 1 = |P({})|, where {} denotes the empty set, we know that 1 satisfies q(n). Therefore, 1 satisfies both p(n) and q(n) and is in the set T(p ∧ q).
The next perfect square less than 100 is 4. To see if 4 satisfies q(n), we need to find a set A such that |P(A)| = 4. We can choose A = {1, 2, 3, 4}, which has 2^4 = 16 subsets. Therefore, 4 satisfies q(n) and is in the set T(p ∧ q).
We can continue this process for each perfect square less than 100 to find the set of positive integers that satisfy both p(n) and q(n). The final set is:
T(p ∧ q) = {1, 4, 9, 16, 25, 36, 49, 64, 81}
Therefore, the set of positive integers that satisfy both p(n) and q(n) is {1, 4, 9, 16, 25, 36, 49, 64, 81}.
To know more about integers, visit: brainly.com/question/15276410
#SPJ4
At the fabric store, you spent $51.30 for 15 yards of fabric. How much did each yard cost
Answers
A line segment has the endpoints U(–6, –5) and V(1, 7). Find the coordinates of its midpoint M.
Answers
Answer:
chhgggggfggghghyuuyyytggfff
What is the product of 329 and 65
Answers
Answer:
The product of 329 and 65 is 21385
Step-by-step explanation:
Product of 329 and 65
329 × 65 = 21385
Thus, The product of 329 and 65 is 21385
-TheUnknownScientist 72
Find the vector equation of the plane determined by the following intersecting line.
L1: r = (0,0,1) + s (-1,0,0); s ∈ R
L2: r = (-3,0,1) + t (0,0,2); t ∈ R
Please solve in detail and with a clear explanation!
Answers
The vector equation of the plane determined by the intersecting lines L₁ and L₂ is r = (0,0,1) + s(-1,0,0) + t(0,0,2); s, t ∈ R.
To find the vector equation of the plane, we need a point on the plane and two direction vectors. The point on the plane can be obtained from either line, and the direction vectors are the direction ratios of each line.
For line L₁, the point (0,0,1) lies on it, and the direction vector is (-1,0,0).
For line L₂, the point (-3,0,1) lies on it, and the direction vector is (0,0,2).
Using these values, we can write the vector equation of the plane as:
r = (0,0,1) + s(-1,0,0) + t(0,0,2)
Expanding the equation, we have:
r = (-s, 0, 1) + (0, 0, 2t)
Combining like terms, we get:
r = (-s, 0, 1 + 2t)
learn more about vector equation here:
https://brainly.com/question/30561769
#SPJ4
Solve the initial value problem below using the method of Laplace transforms. y ′′
+y ′
−30y=0,y(0)=−1,y ′
(0)=39 Click here to view the table of Laplace transforms. Click here to view the table of properties of Laplace transforms. y(t)=3e 5t
−4e −6t
(Type an exact answer in terms of e.)
Answers
The solution to the given initial value problem using the Laplace transform is y(t) = 3e⁻²ᵗ - (19e⁻⁵ᵗ - 3e²ᵗ)u₋ₜ(t). The solution of the given differential equation using Laplace transforms is \(\[y(t)=3{{e}^{-2t}}-\left(19{{e}^{-5t}}-3{{e}^{2t}}\right){{u}_{-t}}\left( t \right)\]\).
First, we will apply Laplace transform to the given ODE. Laplace transform of the given ODE \(\[{y}''+{y} '-30y=0\] \[\Rightarrow \mathcal{L}\left\{ {y}'' \right\}+\mathcal{L}\left\{ {y} ' \right\}-30\mathcal{L}\left\{ y \right\}=0\] \[\Rightarrow s^2\mathcal{L}\left\{ y \right\}-s{y}\left( 0 \right)-{y} ' \left( 0 \right)+s\mathcal{L}\left\{ y \right\}-y\left( 0 \right)-30\mathcal{L}\left\{ y \right\}=0\]\). By putting the given values we get, \(\[{s}^2Y\left( s \right)+1\times s-39+ sY\left( s \right)+1+30Y\left( s \right)=0\] \[\Rightarrow {s}^2Y\left( s \right)+sY\left( s \right)+31Y\left( s \right)=38\] \[\Rightarrow Y\left( s \right)=\frac{38}{s^2+s+31}\] The partial fraction of the above function \[\Rightarrow Y\left( s \right)=\frac{19}{s+5}-\frac{3}{s+(-2)}\]\).
We have to find the inverse Laplace of the given function. Using Laplace transform table: \(\[\mathcal{L}\left\{ e^{at} \right\}=\frac{1}{s-a}\] \[Y\left( s \right)=\frac{19}{s+5}-\frac{3}{s+(-2)}\] \[\Rightarrow Y\left( t \right)=\left(19{{e}^{-5t}}-3{{e}^{2t}}\right)u(t)\] \[\Rightarrow Y\left( t \right)=3{{e}^{-2t}}-\left(19{{e}^{-5t}}-3{{e}^{2t}}\right){{u}_{-t}}\left( t \right)\]\). Thus, the solution of the given differential equation using Laplace transforms is \(\[y(t)=3{{e}^{-2t}}-\left(19{{e}^{-5t}}-3{{e}^{2t}}\right){{u}_{-t}}\left( t \right)\]\).
The solution has been obtained by using the method of Laplace transform. We have given a differential equation of y″ + y′ − 30y = 0, and the initial conditions of the equation are y(0) = −1 and y′(0) = 39. We will solve the given equation using Laplace transform.
Applying Laplace transform to the given differential equation, s²Y(s) - s(y(0)) - y′(0) + sY(s) - y(0) - 30Y(s) = 0We will substitute the given values into the above equation. Therefore, we get s²Y(s) + sY(s) + 31Y(s) = 38Solving for Y(s), we have Y(s) = 38 / (s² + s + 31). To obtain the inverse Laplace of Y(s), we have to break the function into partial fractions. After breaking the function into partial fractions, we get Y(t) = 3e⁻²ᵗ - (19e⁻⁵ᵗ - 3e²ᵗ)u₋ₜ(t).
Learn more about differential equations here:
https://brainly.com/question/30093042
#SPJ11
Write these from smallest to largest
100mm 20cm 0.5cm 0.5m
Answers
Answer:
100mm, 0.5cm, 20 cm, 0.5 m
The number of fish in a lake decreased by 25% between last year and this year. Last year there were 60 fish in the lake. What is the population this year?
Answers
Answer: 45 fish
Step-by-step explanation:
To find the answer you would first convert the percentage into a decimal which would be 25% for this problem. Then you multiply the original price by the decimal. 60 x 0.25=15. Next you would subtract the discount from the original price which would be 60-15=45.
Hope this helped!!
Running at 5 miles an hour how long will it take you to go 12 miles
Answers
Answer:
2 hours and 24 minutes.
7. A rectangular prism measures 7 1/2 cm by 12 cm by 15 1/2 cm. a. Calculate the number of cubes with edge length cm that fit in this prism. b. What is the volume of the prism in cm3? Show your reasoning. If you are stuck, think about how many cubes with -cm edge lengths fit into .
Answers
Answer:
a.The number of cubes with edge length 1/2 cm that fit in this prism= 2520
b. Volume of the prism= 315 cm³
Step-by-step explanation:
Volume of the rectangular prism = length *width * height
= 7 1/2 * 12 * 15 1/2
= 7 * 6* 15 1/2
= 7*3*15
= 315 cm³
Volume of the cube = length *width * height
= 1/2 *1/2 *1/2
= 1/8 cm³
Now number of cubes that would fit in the rectangular prism is given by
= Volume of the prism/ Volume of the cubes
= 315/1/8
= 2520
The number of cubes with edge length cm that fit in this prism= 2520