4. Simplify the expression
-22f+8f-15+9
Answers
Answer:
-22f+8f-15+9
-14f-6
-2(7f+3)
Answer:
-14f -6
Step-by-step explanation:
Add the numbers
-2 2 + 8 − 1 5 + 9
− 2 2 + 8 − 6
Combine like terms
− 2 2 + 8 − 6
− 1 4 − 6
Solution
− 1 4 − 6
hope this helped :)
Related Questions
the study would use a . the study would use simple random sampling because it would be easy to randomly select of . b. the study would use a . the study would use cluster sampling because the of fall into naturally occurring subgroups. c. the study would use a . the study would use stratified sampling because it would be important to have members from each segment of the population. d. the study is a , because the population is for it to be practical to record all of the responses.
Answers
The study would use a simple random sampling because it would be easy to randomly select. The study would use cluster sampling because the of fall into naturally occurring subgroups. The study would use stratified sampling because it would be important to have members from each segment of the population.
The study is a sample survey, because the population is for it to be practical to record all of the responses.
a. The study would use a simple random sampling because it would be easy to randomly select members of the population. Simple random sampling is a type of probability sampling that is used when the population is homogenous and every member has an equal chance of being selected for the sample.
b. The study would use cluster sampling because the members of the population fall into naturally occurring subgroups. Cluster sampling is a type of probability sampling that is used when the population is heterogeneous and can be divided into naturally occurring subgroups.
c. The study would use stratified sampling because it would be important to have members from each segment of the population. Stratified sampling is a type of probability sampling that is used when the population is heterogeneous and can be divided into segments or strata based on certain characteristics.
d. The study is a sample survey, because the population is too large for it to be practical to record all of the responses. Sample survey is a type of survey that collects data from a sample of the population, rather than the entire population. This is often done when the population is too large or when it is not practical to survey the entire population.
To know more about sampling refer here:
https://brainly.com/question/30759604
#SPJ11
Mrs. Gilus is in charge of the budge of the school. Last year, we began the year with $708.88 in our bank account, but by the end of the year we owed $347.99. What rational number can be used to describe the change in the bank account’s balance?
Answers
Answer:
-1056.87
Step-by-step explanation:
You want to know the number that represents the change in a bank balance from +$708.88 to -$347.99.
Change in valueThe change in a value is found by subtracting the beginning value from the ending value:
-$347.99 -708.88 = -$1056.87
The number -1056.87 can be used to describe the change in the account balance.
can someone help me with this?

Answers
Answer:
Step-by-step explanation:
If you write 1 instead of y, x would be 5/8 so ratio is 1/5:8=8/5
A model rocket is launched 25 feet from you.When the rocket is at height h, the distance d between you and the rocket is given by d=\sqrt{625+h^2} where h and d are measured in feet. What is the rocket’s height when the dust between you and the rocket is 100 feet? around to the nearest hundredth.
Answers
The rocket’s height to the nearest hundredth when the distance between you and the rocket is 100 feet is equal to 96.83 feet.
How to calculate the amount of rocket’s height?Based on the information provided, the height h (in feet), of this rocket during its launching with respect to distance d between you and the rocket can be modeled by this quadratic function:
d(h) = √(625 + h²)
Substituting the given parameters into the quadratic function d(h), we have the following;
d(h) = √(625 + h²)
100 = √(625 + h²)
Taking the square of both sides of the quadratic function, we have the following:
100² = [√(625 + h²)]²
10,000 = 625 + h²
Rocket’s height, h² = 10,000 - 625
Rocket’s height, h² = 9,375
Rocket’s height, h = √9,375
Rocket’s height, h = 96.83 feet.
Read more on distance here: brainly.com/question/28353531
#SPJ1
605 and 1152 to the nearest tenth
Answers
Answer:
600 and 1200
Step-by-step explanation:
Suppose a normal distribution has a mean of 62 and a standard deviation of
4. What is the probability that a data value is between 56 and 64? Round your
answer to the nearest tenth of a percent.
Answers
Answer:
62.5%
Step-by-step explanation:
(56 - 62) / 4 = -1.5 z score = 0.0668
(64 - 62) / 4 = 0.5 z score = 0.6915
0.6915 - 0.0668 = 0.6247
Rounded this becomes 62.5%
The probability for the data value in between 56 and 64 is 62.5%.
What is z-score?
The z-score of a value is the count of the numbers of standard deviations between the value and the mean of set.
How to calculate z-score?z-score can be calculated by the formula
z = (x - μ)/σ
where,
μ is the mean
σ is the standard deviation
x is the data point
What is probability?A probability is a number that reflects the chance or likelihood that a particular event will occur.
According to the given question
Mean of a normal distribution, μ = 62
standard deviation of a normal distribution, σ = 4
Now for the data value 56, the z-score will be
z = (56 - 62) / 4 = -1.5 z score = 0.0668
So, the area under normal distribution curve z = -1.5
P(z = -1.5) = 0.0668
Similarly,
For the data value 64, the z-score will be
z-score = (64 - 62) / 4 = 0.5
The area under normal distribution curve z = 0.5 is given by
P( z = 0.5) = 0.69
Therefore, the probability for the data value in between 56 and 64 is given by
0.6915 - 0.0668 = 0.6247 = 62.5%
Hence, the probability for the data value in between 56 and 64 is 62.5%.
Learn more about the z-score and probability here:
https://brainly.com/question/25638875
#SPJ2
assume that we have a non-standard normal distribution with =3 and =2 . using the normal distribution table located here, find p(x>4.5)
Answers
The area to the right of 0.75 (i.e., the probability that z is greater than 0.75) is: 1 - 0.7734 = 0.2266 This means that the probability of getting a value greater than 4.5 in this non-standard normal distribution is approximately 0.2266.
To answer this question, we need to use the normal distribution table. However, since the distribution is non-standard, we need to standardize the value of 4.5 using the formula: z = (x - μ) / σ where μ is the mean and σ is the standard deviation.
Substituting the given values, we get: z = (4.5 - 3) / 2 z = 0.75 Now, we need to find the probability that z is greater than 0.75. Looking at the normal distribution table, we find that the area to the left of 0.75 is 0.7734.
Visit here to learn more about Probability:
brainly.com/question/13604758
#SPJ11
Solve for x: x/2x+3 + 2x+3/x = 184/65
Answers
Answer:
x/2x+3 + 2x +3/x = 184 /65
x(2x + 3)–1 + (2x+3)x-1 = 184/65
(2x + 3)x / (2x +3)x = 184/65
2x² + 3x / 2x² + 3x = 184/65
1x= 184/64
x = 184/64
Step-by-step explanation:
Given that: {x/(2x+3)} + {(2x+3)/x} = 184/65
⇛[{(x*x) + (2x+3)(2x+3)}/{(x)(2x+3)}] = 184/65
⇛[{x² + 2x(2x+3) + 3(2x+3)}/(2x²+3x)] = 184/65
⇛[{x² + 4x² + 6x + 6x + 9}/(2x²+3x)] = 184/65
⇛[{x² + 4x² + 12x + 9}/(2x² + 3x)] = 184/65
⇛{(5x² + 12x + 9)/(2x² + 3x)} = 184/65
On applying cross multiplication then
⇛184(2x² + 3x) = 65(5x² + 12x + 9)
Multiply the number outside of the brackets with numbers and variables in the brackets on LHS and RHS.
⇛388x² + 582x = 325x² + 780x + 584
⇛388x² + 582x -325x² - 780x - 584 = 0
⇛388x²-325x² + 582x-780x - 584 = 0
⇛63x² - 198x - 584 = 0
⇛8(7x² - 22x - 65) = 0
⇛7x² - 22x - 65 = 0
Now,
This is of the form ax² + bx + c = 0, Where, a = 7, b = -22 and c = -65
Using the quadratic formula x = [{-b±√(b²-4ac)}/2a] , we get
x = [{-(-22)±√(-22)² - 4(7)(-65)}/{2(7)]
x = [{-(-22)±√(-22*-22) - 4(7)(-65)}/{2(7)]
x = [{22 ± √(484 + 1820)}/14]
x = [{22 ± √(2304)}/14]
x = {(22 ± 48)/14}
x = {(22 + 48)/14} or {(22 - 48)/14}
x = (70/14) or (-26/14)
x = 5 or x = -13/7
Therefore, x = 5 or -13/7
Answer: Hence, the value of x for the given equation is 5 or -13/7.
Please let me know if you have any other questions.
A particle moves along the x-axis so that at any time t ≥ 0 its velocity is given by the function v(t) = t^2 In(t + 2). What is the acceleration of the particle at time t = 6?
A. 1.500
B. 20.453
C. 29.453
D. 74.860
E 133.417
Answers
A particle moving along the x-axis with velocity given by the function v(t) = t^2 In(t + 2). The acceleration of the particle at time t = 6 is approximately 29.453.
To find the acceleration of the particle at time t = 6, we need to calculate the derivative of the velocity function v(t).
Given: v(t) = t^2 * ln(t + 2)
To find the derivative, we use the product rule and the chain rule. The derivative of v(t) is denoted as a(t) (acceleration):
a(t) = (2t * ln(t + 2)) + (t^2 * (1/(t + 2)))
Now, substitute t = 6 into the acceleration function to find the acceleration at time t = 6:
a(6) = (2 * 6 * ln(6 + 2)) + (6^2 * (1/(6 + 2)))
= (12 * ln(8)) + (36 * (1/8))
= 12 * ln(8) + 4.5
Calculating this expression, we find that a(6) is approximately 29.453.
Therefore, the acceleration of the particle at time t = 6 is approximately 29.453.
To know more about x-axis, click here: brainly.com/question/2491015
#SPJ11
The volume of this cone is 1,610.82 cubic meters. What is the radius of the cone?

Answers
\(\\ \sf\longmapsto V=1610.82\)
\(\\ \sf\longmapsto \dfrac{1}{3}\pi r^2h=1610.82\)
\(\\ \sf\longmapsto \pi r^2(19)=1610.82(3)=4832.36\)
\(\\ \sf\longmapsto 3.14r^2=254.34\)
\(\\ \sf\longmapsto r^2=81\)
\(\\ \sf\longmapsto r=9m\)
let f(x, y) be a function such that • the limit of f(x, y) as x → 0 along the path y = x is 0. • the limit of f(x, y) as x → 0 along the path y = x 2 is 0.
Answers
The function f(x, y) satisfies the conditions that its limit approaches zero as x approaches zero along two different paths: y = x and y = x^2. This implies that as x approaches zero, the function f(x, y) must approach zero regardless of whether y varies linearly or quadratically with x.
The given conditions state that the limit of f(x, y) as x approaches zero along the path y = x is zero. This means that as x gets arbitrarily close to zero, the function f(x, y) approaches zero when y varies linearly with x. Similarly, the second condition states that the limit of f(x, y) as x approaches zero along the path y = x^2 is also zero. This implies that when y varies quadratically with x, the function f(x, y) still approaches zero as x approaches zero. Therefore, the function f(x, y) must satisfy both conditions by converging to zero as x approaches zero along both paths.
To learn more about function click here: brainly.com/question/30721594
#SPJ11
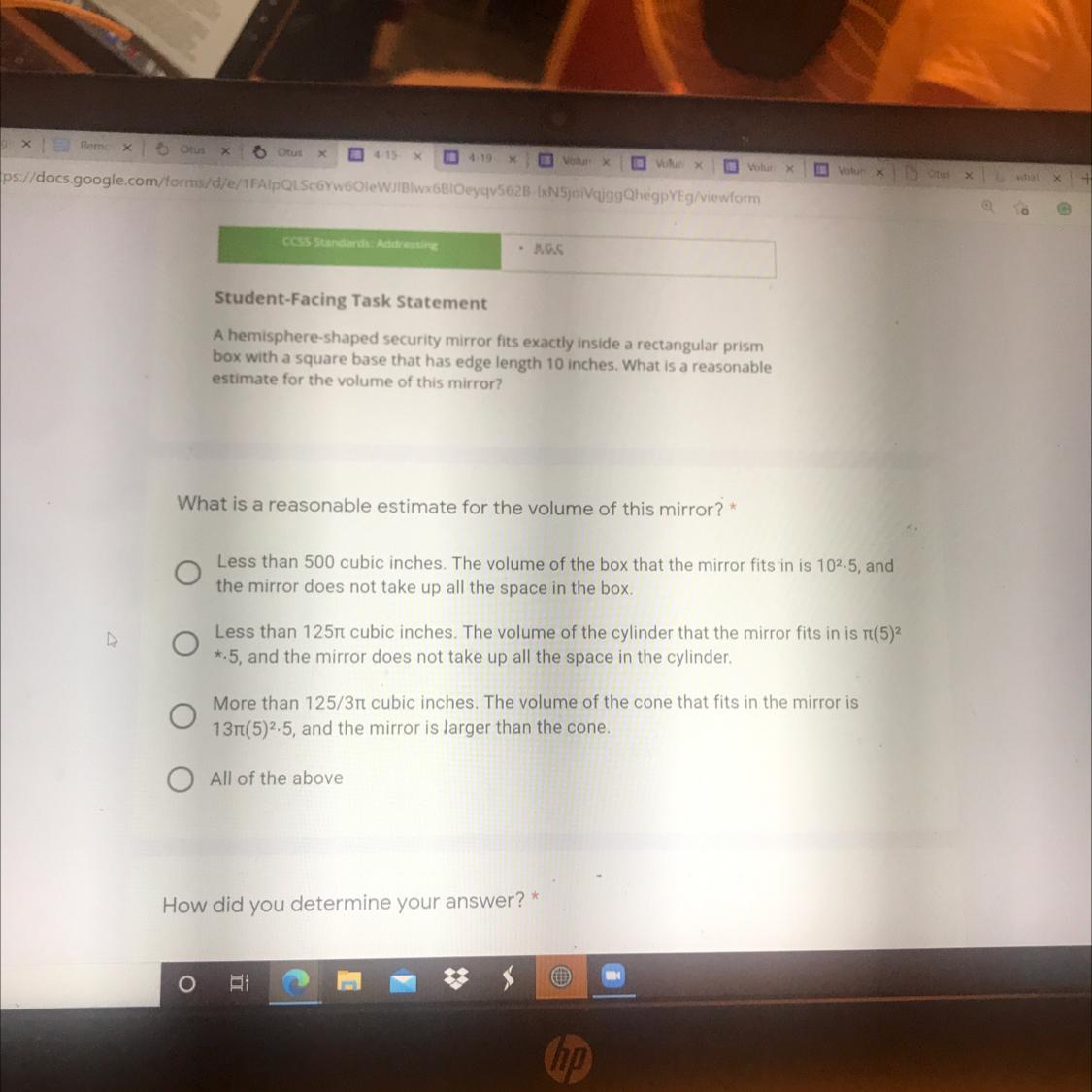
A hemisphere-shaped security mirror fits exactly inside a rectangular prism
box with a square base that has edge length 10 inches. What is a reasonable
estimate for the volume of this mirror?
What is a reasonable estimate for the volume of this mirror? *
Less than 500 cubic inches. The volume of the box that the mirror fits in is 102.5, and
the mirror does not take up all the space in the box.
Less than 12511 cubic inches. The volume of the cylinder that the mirror fits in is ri(5)2
*.5, and the mirror does not take up all the space in the cylinder.
More than 125/31 cubic inches. The volume of the cone that fits in the mirror is
131(5)2.5, and the mirror is larger than the cone.
O All of the above
Answers
If the length of a rectangle is decreased by 4 cm and the width is increased by 5 cm, the result will be a square. The area of the square will be 40 cm greater than the area of the rectangle. Find the area of the rectangle.
Answers
The area of the rectangle is found to be 20 - 2·√(10) sq. units.
Explain about the area of rectangle?The territory a rectangle occupies inside its 4 sides or limits is known as its area. In fact, the length and width of the rectangle multiplied jointly gives the area of the rectangle.Let x be the length of the rectangle.
Let y be the width of rectangle.
Then, length is reduced by 4 and with is increased by 5.
x - 4 = y + 5 , (becomes square) ....eq 1
Area of square = 40 cm²
Then,
(x - 4) × (y + 5) = 40 cm²
From eq 1
(y + 5) × (y + 5) = 40 cm²
y² + 10y + 25 = 40
y² + 10y + 25 - 40 = 0
y² + 10y - 15 = 0
Solving equation by quadratic formula:
y = -5 + 2·√(10)
Then, for x:
x - 4 = 5 + -5 + 2·√(10) = 2·√(10)
x = 4 + 2·√(10)
Now,
Area of the rectangle, A = x × y
Put the values:
A = (-5 + 2·√(10)) × (4 + 2·√(10))
A = 20 - 2·√(10)
Thus, the area of the rectangle is found to be 20 - 2·√(10) sq. units.
Know more about area of rectangle,
https://brainly.com/question/2607596
#SPJ1
Answer: 360cm^2
Step-by-step explanation: the rectangle is 24 by 15
how much time is required to compute f(x) = ∑^n _i=0 a_ix^i a. using a simple routine to perform exponentiation? b. using the routine in 2.4.4?
Answers
The time required to compute f(x) = ∑^n _i=0 a_ix^i depends on the routine used to perform exponentiation.
a. Using a simple routine to perform exponentiation, the time required to compute f(x) would be O(n), since we would have to perform exponentiation n times for each term in the sum.
b. Using the routine in 2.4.4, the time required to compute f(x) would be O(log n), since the routine uses a divide-and-conquer approach to perform exponentiation, which reduces the number of computations required.
Therefore, the time required to compute f(x) depends on the routine used to perform exponentiation. Using a simple routine, the time required would be O(n), while using the routine in 2.4.4, the time required would be O(log n).
Learn more about exponentiation
brainly.com/question/28596571
#SPJ11
what is the value of x?

Answers
Answer:
x = 9
Step-by-step explanation:
12^2+x^2 = 15^2
==> x = 9
Answer:
9
Step-by-step explanation:
x = \(\sqrt{c^{2} - a^{2} }\)
x = \(\sqrt{15^{2} - 12^{2} }\)
x = \(\sqrt{225 - 144}\)
x = \(\sqrt{81}\)
x = 9
A fair die is rolled once. Let A={1,3,5}, B ={2,4,6),C={1,2,3,4}. Which two events are independent? Choose all that is correct. A and C are independent. B and C are independent. A and B are independent. All events are dependent of each other.
Answers
Among the given events, A and C are independent.
Two events are considered independent if the occurrence or non-occurrence of one event does not affect the probability of the other event happening. Let's analyze the given events:
A = {1, 3, 5}: This event consists of the outcomes of rolling an odd number on the fair die.
B = {2, 4, 6}: This event consists of the outcomes of rolling an even number on the fair die.
C = {1, 2, 3, 4}: This event consists of the outcomes of rolling a number from 1 to 4 on the fair die.
To determine if events A and C are independent, we need to check if the probability of A intersection C (the outcomes that satisfy both A and C) is equal to the product of their individual probabilities.
P(A) = 3/6 = 1/2 (since there are 3 favorable outcomes out of 6 possibilities)
P(C) = 4/6 = 2/3 (since there are 4 favorable outcomes out of 6 possibilities)
P(A intersection C) = 2/6 = 1/3 (since there are 2 outcomes common to both A and C: {1, 3})
Since P(A) * P(C) = (1/2) * (2/3) = 1/3 = P(A intersection C), we can conclude that events A and C are independent.
However, events B and C are not independent because the occurrence of B (rolling an even number) affects the probability of C (rolling a number from 1 to 4) since the outcomes in B are not part of C. Similarly, events A and B are also not independent because the occurrence of A (rolling an odd number) affects the probability of B (rolling an even number).
Therefore, the correct answer is that A and C are the two independent events among the given options.
Learn more about probability here:
https://brainly.com/question/33406519
#SPJ11
Which of the following points is a solution to the system of inequalities below?
Y>3x-1
(1,0) (0,1) (2,1) (1,1)
Answers
Answer:
(0, 1)
Step-by-step explanation:
y > 3x - 1
When x = 0: y > (3 x 0) - 1 ⇒ y > -1
When x = 1: y > (3 x 1) - 1 ⇒ y > 2
When x = 2: y > (3 x 2) - 1 ⇒ y > 5
Therefore the only point that satisfies this is (0, 1)
Answer:
(0, 1)Step-by-step explanation:
Attached is the graphical solution.
We can see one point is within the shaded area - (0, 1), all the others are outside.

Use logarithmic differentiation to find the derivative of the function. y=(ln(x+4)) x
Answers
the derivative of the function y = (ln(x + 4))x using logarithmic differentiation is given by y' = (ln(x + 4))x * [ln(ln(x + 4)) + (1/ln(x + 4)) * (1/(x + 4))].
To find the derivative of the function y = (ln(x + 4))x using logarithmic differentiation, we can follow these steps:
Step 1: Take the natural logarithm of both sides of the equation:
ln(y) = ln((ln(x + 4))x)
Step 2: Use the logarithmic property ln(a^b) = b ln(a) to simplify the right-hand side of the equation:
ln(y) = x ln(ln(x + 4))
Step 3: Differentiate both sides of the equation implicitly with respect to x:
(1/y) * y' = ln(ln(x + 4)) + x * (1/ln(x + 4)) * (1/(x + 4))
Step 4: Simplify the expression on the right-hand side:
y' = y * [ln(ln(x + 4)) + (1/ln(x + 4)) * (1/(x + 4))]
Step 5: Substitute the original expression of y = (ln(x + 4))x back into the equation:
y' = (ln(x + 4))x * [ln(ln(x + 4)) + (1/ln(x + 4)) * (1/(x + 4))]
Therefore, the derivative of the function y = (ln(x + 4))x using logarithmic differentiation is given by y' = (ln(x + 4))x * [ln(ln(x + 4)) + (1/ln(x + 4)) * (1/(x + 4))].
To know more about Equation related question visit:
https://brainly.com/question/29538993
#SPJ11
Jordan’s family went to dinner and bought four meals for $8.00 each. They had a coupon for 25% off. What was their total bill after the coupon
Answers
Answer:
1558.99
Step-by-step explanation:
Is l = 3 arbitrary? that is, is l = 3 the result of some aspect of the structure of the floating rate tranche? demonstrate your answer
Answers
The value l = 3 is not arbitrary and is indeed a result of some aspect of the structure of the floating rate tranche. This value is determined by the specific terms and conditions outlined in the tranche agreement.
In a floating rate tranche, the interest rate is adjusted periodically according to a reference index, such as LIBOR or EURIBOR, plus a margin or spread (l). In this case, l = 3 represents the margin added to the reference index to determine the overall interest rate payable.
This value is established by the issuer based on various factors such as credit quality, market conditions, and the issuer's own funding costs.
1. The floating rate tranche's interest rate is determined by a reference index plus a margin (l).
2. In this case, l = 3 is the margin added to the reference index.
3. The value of l is established by the issuer, considering credit quality, market conditions, and funding costs.
4. Therefore, l = 3 is not arbitrary and is a result of the structure of the floating rate tranche.
To know more about interest rate click on below link:
https://brainly.com/question/13324776#
#SPJ11
when summarizing heavily skewed data, the best measure of central tendency is:
Answers
When summarizing heavily skewed data, the best measure of central tendency is the median.
In situations where the data distribution is heavily skewed, the mean may not accurately represent the central tendency of the data. Skewness refers to the asymmetry of the data distribution, where the tail of the distribution extends more to one side. When data is heavily skewed, it can be influenced by extreme values, leading to an unbalanced representation of central tendency if the mean is used.
The median, on the other hand, is less affected by extreme values and provides a better measure of central tendency for skewed data. The median represents the middle value in a data set when the observations are arranged in ascending or descending order. Unlike the mean, it is not influenced by extreme values, making it a robust measure for summarizing skewed data.
By using the median, we can capture the central value that is more representative of the majority of the data points, even in the presence of outliers or skewed distributions. It provides a better understanding of the typical value or position within the data set, regardless of extreme values or asymmetric distributions.
Therefore, when summarizing heavily skewed data, the median is considered the best measure of central tendency as it provides a more accurate representation of the center of the distribution and is less influenced by extreme values.
Learn more about median here:
https://brainly.com/question/11237736
#SPJ11
I NEED HELP WITH MATH

Answers
Answer:
B and D
Step-by-step explanation:
When you subtract a negative number, you are adding.
7-(-7)=7+7=14
Adding goes right on a number line.
plss plss help mee :0
find the range of the function y=3-x when the domain is (-2,0,3)
Answers
Answer:
y=3−x
(−2,0,3)
Use Gaussian elimination to determine the solution set to the
given system.
4. 3x₁ +5x₂ + x3 = 3, 2x1 + 6x2 + 7x3 = 1. 3x1 - x2 1, 4, 5. 2x₁ + x₂ + 5x3 : 7x15x28x3 = -3. 3x₁ + +5x2 5x₂x3 = 14, x₁ + 2x2 + x3 = 3, 2x1 + 5x2 + 6x3 = 2. 6.
Answers
Solution set of the given system of equations is {(-11/3, -1/3, 1)}.Hence, this is the solution set to the given system of equations using Gaussian elimination.
Gaussian Elimination method: The system of equations can be transformed into an equivalent system of equations through a sequence of operations such as switching rows, multiplying rows, or adding a multiple of one row to another row.
These operations do not affect the solution set of the original system.
These steps are repeated until the system of equations is in a simpler form that can be solved by substitution method.
Here is the main answer to the given problem:
3x₁ +5x₂ + x3 = 32x1 + 6x2 + 7x3
= 13x₁ - x₂ + x₃ = 15x₁ + 2x₂ + 8x₃ = -2.
Add (-1/3) * R₁ to R₂Add (-3) * R₁ to R₃R₁ remains the same
5x₂ + 20/3 x₃ = -62x₂ + 2/3 x₃
= 1R₃ = 0x₂ + 14/3 x₃
Hence, Solution set of the given system of equations is {(-11/3, -1/3, 1)}.Hence, this is the solution set to the given system of equations using Gaussian elimination.
learn more about equations click here:
https://brainly.com/question/2972832
#SPJ11
A roofing contractor uses shingles at a rate of 3 bundles for every 96 square feet of roof covered. At this rate, how many bundles of shingles will he need in order to cover a roof that is 416 square feet?
Answers
Answer:
13
Step-by-step explanation:
416/96 = 4.33333
416 is 4.333 times 96, so he needs 4.333 times 3 bundles.
4.3333 × 3 = 13
Answer: 13
Answer:
13
Step-by-step explanation:
you see how much it covers initially. (96/3=32) then 416/32=13
Solve for x.
\(4x+6=10-4\)
Answers
Steps to solve:
4x + 6 = 10 - 4
~Simplify
4x + 6 = 6
~Subtract 6 to both sides
4x = 0
~Divide 4 to both sides
x = 0
Best of Luck!
Answer:
\(\large\boxed{x = 0}\)
Step-by-step explanation:
4x + 6 = 10 - 4
Subtract 10 - 4
4x + 6 = 6
Subtract 6 from both sides of the equation
4x = 0
Divide both sides of the equation by 4
\(\large\boxed{x = 0}\)
Hope this helps :)
Come answer this question please

Answers
Answer:
You cannot combine -5x^2 and 2x.
Step-by-step explanation:
You cannot combine -5x^2 and 2x. They are not like terms
x^2 and x are not the same
Write tan 41π/36 in terms of the tangent of a positive acute angle.
Answers
tan(41π/36) can be written in terms of the tangent of a positive acute angle as (tan((1/9)π) + tan((37/36)π)) / (1 - tan((1/9)π)tan((37/36)π))
To express tan(41π/36) in terms of the tangent of a positive acute angle, we need to find an angle within the range of 0 to π/2 that has the same tangent value.
First, let's simplify 41π/36 to its equivalent angle within one full revolution (2π):
41π/36 = 40π/36 + π/36 = (10/9)π + (1/36)π
Now, we can rewrite the angle as:
tan(41π/36) = tan((10/9)π + (1/36)π)
Next, we'll use the tangent addition formula, which states that:
tan(A + B) = (tan(A) + tan(B)) / (1 - tan(A)tan(B))
In this case, A = (10/9)π and B = (1/36)π.
tan(41π/36) = tan((10/9)π + (1/36)π) = (tan((10/9)π) + tan((1/36)π)) / (1 - tan((10/9)π)tan((1/36)π))
Now, we need to find the tangent values of (10/9)π and (1/36)π. Since tangent has a periodicity of π, we can subtract or add multiples of π to get equivalent angles within the range of 0 to π/2.
For (10/9)π, we can subtract π to get an equivalent angle within the range:
(10/9)π - π = (1/9)π
Similarly, for (1/36)π, we can add π to get an equivalent angle:
(1/36)π + π = (37/36)π
Now, we can rewrite the expression as:
tan(41π/36) = (tan((1/9)π) + tan((37/36)π)) / (1 - tan((1/9)π)tan((37/36)π))
Since we are looking for an angle within the range of 0 to π/2, we can further simplify the expression as:
tan(41π/36) = (tan((1/9)π) + tan((37/36)π)) / (1 - tan((1/9)π)tan((37/36)π))
Therefore, tan(41π/36) can be written in terms of the tangent of a positive acute angle as the expression given above.
For more about tangent:
https://brainly.com/question/19064965
#SPJ4
Find the volume
of the figure below:

Answers
Step-by-step explanation:
Use Pythagorean theorem to find the base of the right triangle
221^2 = 195^2 + b^2
b = 104 km
triangle area = 1/2 base * height = 1/2 * 104 * 195 = 10140 km^2
Now multiply by the height to find volume
10140 km^2 * 15 km = 152100 km^3
MATH PLS HELPPP FREE BRAINLIEST!!!!!!!!!!!!!!!!!!

Answers
All real numbers is the answer
Answer:
All real numbers is the Answer
Step-by-step explanation: