4. The graph of a linear function is shown. Which best
describes the slope of the line?
A. Zero Slope
B. Undefined Slope
C. Negative Slope
D. Positive Slope

Answers
Related Questions
Function \(y = f(x)\) is continuous on \(R\).
The function satisfy \(f(x)+x=\int\limits^2_0 {[f(x)-x]} \, dx\)
∀\(x\)∈\(R\).
Find the value of m so that \(\int\limits^2_0 {[mx+f(x)]} \, dx=0\).
A. m = -2
B. m = 0
C. m = -3
D. m = -1
Answers
The value of m so that the condition satisfies is -2, the correct option is A.
We are given that;
y=f(x) is continuous
Now,
To find the numbers c that satisfy the conclusion of the Mean Value Theorem, we need to solve the equation:
f’© = [f(2) - f(0)] / (2 - 0)
f’(x) = 8x - 2
f(2) = 4(2)^2 - 2(2) + 3 = 23
f(0) = 4(0)^2 - 2(0) + 3 = 3
f’© = (23 - 3) / (2 - 0)
f’© = 10
8m - 2 = 10
8m = 12
m = 12/8
m = -2
Therefore, by the given function the answer will be -2.
Learn more about function here:
https://brainly.com/question/2253924
#SPJ1
Which set of transformations is needed to graph f(x) = –2sin(x) + 3 from the parent sine function?
vertical compression by a factor of 2, vertical translation 3 units up, reflection across the y-axis
vertical compression by a factor of 2, vertical translation 3 units down, reflection across the x-axis
reflection across the x-axis, vertical stretching by a factor of 2, vertical translation 3 units up
reflection across the y-axis, vertical stretching by a factor of 2, vertical translation 3 units down
Answers
The main function is given by:
f (x) = sine (x)
We then have the following transformations:
Reflections:
Reflection or turning is the mirror image of a figure. It can also be said that it is the turning of points and graphs around the axes.
To graph y = -f (x), reflect the graph of y = f (x) on the x-axis. (Vertical reflection)
f (x) = - sine (x)
Expansions and vertical compressions:
To graph y = a*f (x)
If a> 1, the graph of y = f (x) is expanded vertically by a factor a.
f (x) = - 2 * sine (x)
Vertical translations
Suppose that k> 0
To graph y = f (x) + k, move the graph of k units up.
f (x) = - 2 * sine (x) + 3
Answer:
C. reflection across the x-axis, vertical stretching by a factor of 2, vertical translation 3 units up
The set of transformations which is needed to graph f(x) = –2sin(x) + 3 is reflection across the x-axis, vertical stretching by a factor of 2, vertical translation 3 units up, the correct option is C.
What is rigid transformation?A rigid transformation (also called an isometry) is a transformation of the plane that preserves length. In a rigid transformation the pre-image and image are congruent (have the same shape and sizes).
We are given that;
The function= f(x) = –2sin(x) + 3
Now,
To graph f(x) = –2sin(x) + 3 from the parent sine function y = sin(x), we need to apply the following transformations:
A reflection across the x-axis, because of the negative sign in front of the 2.
A vertical stretching by a factor of 2, because of the absolute value of the coefficient of sin(x), which is 2.
A vertical translation 3 units up, because of the constant term 3.
Therefore, by transformations answer will be Reflection across the x-axis, vertical stretching by a factor of 2, vertical translation 3 units up.
Learn more about rigid transformations;
https://brainly.com/question/7070983
#SPJ5
unit 7 right triangle and trigonometry quiz 7-2
Answers
Yes, trigonometry only works on the right angled triangles.
Explain about the Right triangle and trigonometry?The study of correlations between triangles' side lengths and angles is known as trigonometry.
A triangle with one right angle is referred to as a right triangle as well as right-angled triangle. Trigonometry's foundation is the relationship between a right triangle's sides and angles.The area of mathematics called trigonometry deals with calculating triangles' unknowable sides and angles.There are numerous uses for trigonometry in both engineering and science. We will just provide a couple of instances from surveying as well as navigation in this section.Thus, the right angle, or 90°, is always one angle. The hypotenuse is the side with the 90° angle opposite. The longest side is always the hypotenuse. The other two inner angles add up to 90 degrees.
know more about Right triangle and trigonometry
https://brainly.com/question/20367642
#SPJ1
The complete question is-
Right triangle and trigonometry:
Does trigonometry work on right triangles?
A landscaper is designing a display of flowers for an area in a public park. The flower seeds will be planted at points that lie on a circle that has a diameter of 8 feet. the point where any seed is planted must be 2 feet away from the seeds on either side of it. what is the maximum number of flower seeds that can be planted using the design?
after planting the flower seeds the landscaper has 20 seeds left over. the landscaper wants to plant all of the remaining seeds in another circle so that the seeds are 2 feet apart. what is the diameter of the smallest circle that the landscaper can use to plant all of the remaining seeds?
Answers
The z-score for P(? ≤ z ≤ ?) = 0.60 is approximately 0.25.
The z-score for P(z ≥ ?) = 0.30 is approximately -0.52.
How to find the Z score
P(Z ≤ z) = 0.60
We can use a standard normal distribution table or a calculator to find that the z-score corresponding to a cumulative probability of 0.60 is approximately 0.25.
Therefore, the z-score for P(? ≤ z ≤ ?) = 0.60 is approximately 0.25.
For the second question:
We want to find the z-score such that the area under the standard normal distribution curve to the right of z is 0.30. In other words:
P(Z ≥ z) = 0.30
Using a standard normal distribution table or calculator, we can find that the z-score corresponding to a cumulative probability of 0.30 is approximately -0.52 (since we want the area to the right of z, we take the negative of the z-score).
Therefore, the z-score for P(z ≥ ?) = 0.30 is approximately -0.52.
Read more on Z score here: brainly.com/question/25638875
#SPJ1
Please help me I'm stuck. I will give 30 points for this one. Given triangle ABC tilde triangle PQR and your scale factor Complete the hotspots for these similar triangles and show work

Answers
The value for the hotspots of the similar triangles ∆ABC and ∆PWR are:
(1). angle B = 68°
(2). PQ = 5cm
(3). BC = 19.5cm
(4). area of ∆PQR = 30cm²
What are similar trianglesSimilar triangles are two triangles that have the same shape, but not necessarily the same size. This means that corresponding angles of the two triangles are equal, and corresponding sides are in proportion.
(1). angle B = 180 - (22 + 90) {sum of interior angles of a triangle}
angle B = 68°
Given that the triangle ∆ABC is similar to the triangle ∆PQR.
(2). PQ/7.5cm = 12cm/18cm
PQ = (12cm × 7.5cm)/18cm {cross multiplication}
PQ = 5cm
(3). 13cm/BC = 12cm/18cm
BC = (13cm × 18cm)/12cm {cross multiplication}
BC = 19.5cm
(4). area of ∆PQR = 1/2 × 12cm × 5cm
area of ∆PQR = 6cm × 5cm
area of ∆PQR = 30cm²
Therefore, the value for the hotspots of the similar triangles ∆ABC and ∆PWR are:
(1). angle B = 68°
(2). PQ = 5cm
(3). BC = 19.5cm
(4). area of ∆PQR = 30cm²
Read more about similar triangles here:https://brainly.com/question/14285697
#SPJ1
Why a sample is always smaller than a population?
Answers
Answer:
A sample is a subset of the population.
use stokes theorem to evaluate ∫cf⋅dr where f(x,y,z)=(2y,xz, x y), z =y 3, x^2 y^2) and C is the triangle with vertices (2,0,0), (0,2,0), and (0,0,2) oriented counterclockwise as viewed from above.
Answers
The value of the line integral ∫cf⋅dr is (-2 + y) * sqrt(3).
To evaluate the line integral ∫cf⋅dr using Stokes' theorem, we first need to find the curl of the vector field f. The curl of f is given by ∇ × f, where ∇ is the del operator.
Calculating the curl of f:
\(∇ × f = (∂/∂y)(xz) - (∂/∂z)(2y) + (∂/∂z)(xy) - (∂/∂x)(xy) + (∂/∂x)(2y) - (∂/∂y)(2y)\)
\(= x - 2 - x + 2y - y\\= -2 + y\).
Now, let's find the area of triangle C using the vertices given. The triangle with vertices (2,0,0), (0,2,0), and (0,0,2) forms an equilateral triangle in the xy-plane with side length 2.
The area of an equilateral triangle is given by\((sqrt(3)/4) * (side length)^2\), so the area of this triangle is \((sqrt(3)/4) * (2)^2 = sqrt(3)\).
Since we have the curl of f as -2 + y and the area of the triangle as sqrt(3), we can now evaluate the line integral using Stokes' theorem:
∫cf⋅dr = ∬S (∇ × f) ⋅ dS
= ∬S (-2 + y) ⋅ dS
= (-2 + y) ∬S dS
= (-2 + y) * sqrt(3).
Therefore, the value of the line integral ∫cf⋅dr is (-2 + y) * sqrt(3).
To learn more about line integral from the given link
https://brainly.com/question/25706129
#SPJ4
Landon and Ella eat dinner at Billy's BBQ the cost of dinner was $25.50 they left the waiter a 20% tip. How much money did Landon and Ella leave for the tip?
Answers
Answer:
5.10
Step-by-step explanation:
HELP!!!!! Please. I really need it.

Answers
Let's call the price of the motorcycle "x".
We know that Lenny paid 12.5% in tax, which is the same as 0.125 as a decimal.
To find out how much tax Lenny paid, we can multiply the price of the motorcycle by 0.125:
0.125x = $1437.50
Now we can solve for x by dividing both sides by 0.125:
x = $11,500
Therefore, the price of the motorcycle, not including tax, was $11,500.
Answer:
Your question is:
1437.5 is 12.5% of what number?
1437.5 = 0.125x
x = 1437.5/.125 = $11,500
Therefore, the answer is $11,500!
Step-by-step explanation:
Please brainliest if the helped you a lot! And tell me if I am wrong! I would be so sorry if it was wrong! :D
Can someone please answer this ASAP. (No FAKE LINKS)

Answers
Half of the text is covered...
Answer:
Good Luck!
Step-by-step explanation:
You would add 16 to both side in the attempt of completing the square
Step 1: Move any constant number (this case, it's 35) to the other side
Step 2: You will have a format of ax2 + bx = c, where your a = 1, b = 8, and c = 35
*a must always be 1*
Step 3: Divide b by 2 and then square that number. Your b = 8, so 8/2 is 4. Squaring 4 gives you 16.
Hence, that's why you add 16 to both side from your question.
an object is launched at 9.8 meters per second from a 73.5 meter tall platform, the objects height, s (in meters) after t seconds given by the equation s(t)=-4.9t^2 - 9.8t + 73.5. When does the object strike the ground?
Answers
Hence, in answering the stated question, we may say that Because time equation in this environment cannot be negative, the item hits the ground after 3 seconds.
What is equation?A math equation is a method that links two claims and represents equivalence using the equals sign (=). An equation is a mathematical statement that establishes the equivalence of two mathematical expressions in algebra. In the equation 3x + 5 = 14, for example, the equal sign separates the numbers 3x + 5 and 14. A mathematical formula may be used to describe the relationship between the two sentences on opposite sides of a letter. In usually, the logo and the programme are the same. For instance, 2x - 4 equals 2.
We may utilise the above equation for the item's height, s(t), to determine when the object hits the earth.
Because the object's height will be zero when it hits the ground, we may set s(t) = 0 and solve for t:
\(0 = -4.9t^2 - 9.8t + 73.5\\0 = t^2 + 2t - 15\\t = (-2 + \sqrt(2^2 - 4(1)(-15))) / 2 (1)\\t = (-2 + \sqrt(64)) / 2 \st = (-2 + 8) / 2\)
As a result, the two potential values of t are:
t = (-2 + 8) / 2 = 3
t = (-2 - 8) / 2 = -5
Because time in this environment cannot be negative, the item hits the ground after 3 seconds.
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
We can disregard the negative value since time cannοt be negative in this cοntext, sο the οbject will hit the grοund after 3 secοnds.t = -5 οr t = 3.
What is equatiοn?A mathematical equatiοn is a methοd fοr cοnnecting twο assertiοns and denοting equivalence with the equals sign (=). In algebra, an equatiοn is a mathematical statement that prοves the equality οf twο mathematical expressiοns.
The equatiοn fοr the height οf the οbject as a functiοn οf time is given by:
\(s(t) = -4.9t^2 - 9.8t + 73.5\)
The οbject will hit the grοund when its height is equal tο zerο, sο we can set s(t) equal tο zerο and sοlve fοr t:
\(0 = -4.9t^2 - 9.8t + 73.5\)
Dividing bοth sides by -4.9 tο simplify:
\(0 = t^2 + 2t - 15\)
This is a quadratic equatiοn in t that can be factοred as:
0 = (t + 5)(t - 3)
Therefοre, t = -5 οr t = 3. We can disregard the negative value since time cannοt be negative in this cοntext, sο the οbject will hit the grοund after 3 secοnds.
To know more about equation visit:
brainly.com/question/649785
#SPJ1
(ILL MARK BRAINLIEST) The following two-way table shows the data for the students of two different grades in a school:
Member of Public Library Not Member of Public Library Total
Grade 6
25
3
28
Grade 7
23
7
30
Total
48
10
58
Based on the relative row frequency, the students of which grade are more likely to be members of the public library?
Answers
Answer:
6th
Step-by-step explanation:
the chart says not, 7th has majority
∂²p/∂r² + 1/r ∂p/∂r = ϕμC/k ∂p/∂t
derivation of equations
1-partial derivative diffusivity equation spherical flow
2- partial derivative diffusivity equation hemi- spherical flow
Answers
The partial derivative diffusivity equation for spherical flow is ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t, and for hemispherical flow, it is the same equation.
1. The partial derivative diffusivity equation for spherical flow is derived from the spherical coordinate system and applies to radial flow in a spherical geometry. It can be expressed as ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t.
2. The partial derivative diffusivity equation for hemispherical flow is derived from the hemispherical coordinate system and applies to radial flow in a hemispherical geometry. It can be expressed as ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t.
1. For the derivation of the partial derivative diffusivity equation for spherical flow, we consider a spherical coordinate system with the radial direction (r), the azimuthal angle (θ), and the polar angle (φ). By assuming steady-state flow and neglecting the other coordinate directions, we focus on radial flow. Applying the Laplace operator (∇²) in spherical coordinates, we obtain ∇²p = (1/r²) (∂/∂r) (r² ∂p/∂r). Simplifying this expression, we arrive at ∂²p/∂r² + (1/r) ∂p/∂r.
2. Similarly, for the derivation of the partial derivative diffusivity equation for hemispherical flow, we consider a hemispherical coordinate system with the radial direction (r), the azimuthal angle (θ), and the elevation angle (ε). Again, assuming steady-state flow and neglecting the other coordinate directions, we focus on radial flow. Applying the Laplace operator (∇²) in hemispherical coordinates, we obtain ∇²p = (1/r²) (∂/∂r) (r² ∂p/∂r). Simplifying this expression, we arrive at ∂²p/∂r² + (1/r) ∂p/∂r.
In both cases, the term ϕμC/k ∂p/∂t represents the source or sink term, where ϕ is the porosity, μ is the fluid viscosity, C is the compressibility, k is the permeability, and ∂p/∂t is the change in pressure over time.
These equations are commonly used in fluid mechanics and petroleum engineering to describe radial flow behavior in spherical and hemispherical geometries, respectively.
To learn more about partial derivative, click here: brainly.com/question/2293382
#SPJ11
A telephone long distance carrier charges customers $0.99 for the first 30 minutes and then $0.04 for each minute beyond 30 minutes. If Mary uses this carrier, how long can she talk for $6.00?
Answers
The total that Mary has initially is:
$6.00
Since the first 30 minutes cost $0.99, after those 30 minutes she will have:
$6.00 - $0.99 = $5.01
So far she has talked for 30 minutes but has $5.01 left.
After 30 minutes, the cost per minute is $0.04. To find the number of minutes that she can talk with those $0.04, we divide 5.01 by 0.04:
\(\frac{5.01}{0.04}=125.25\)Using the remaining amount she can talk for 125.25 minutes more.
Thus, the total of minutes is:
\(30+125.25=155.25\)Answer: She can talk for 155.25 minutes.
PO
What is the slope of a line that goes through the following 2 points?
(-12,-5) (0, -8)
Answers
Answer:
-1/4
Step-by-step explanation:
m=(y2-y1)/(x2-x1)
m=(-8-(-5))/(0-(-12))
m=(-8+5)/(0+12)
m=-3/12
simplify
m=-1/4
Please mark me as Brainliest if you're satisfied with the answer.
The test scores for the students in Mr. Miller’s math class are shown here.
52, 61, 69, 76, 82, 84, 85, 90, 94
What is the range of the test scores?
Answers
The range of the test scores in Mr. Miller's math class is 42.
What is the range?Mathematically, the range refers to the difference between the highest value and the lowest value in a data set.
The range is computed by subtraction of the lowest value from the highest value.
Mr. Miller can use the range to measure the spread or dispersion of the test scores.
Test Scores:
52, 61, 69, 76, 82, 84, 85, 90, 94
Highest score = 94
Lowest score = 52
Range = 42 (94 - 52)
Thus, we can conclude that for the math students in Mr. Miller's class, the range of their test scores is 42.
Learn more about the range at https://brainly.com/question/24326172.
#SPJ1
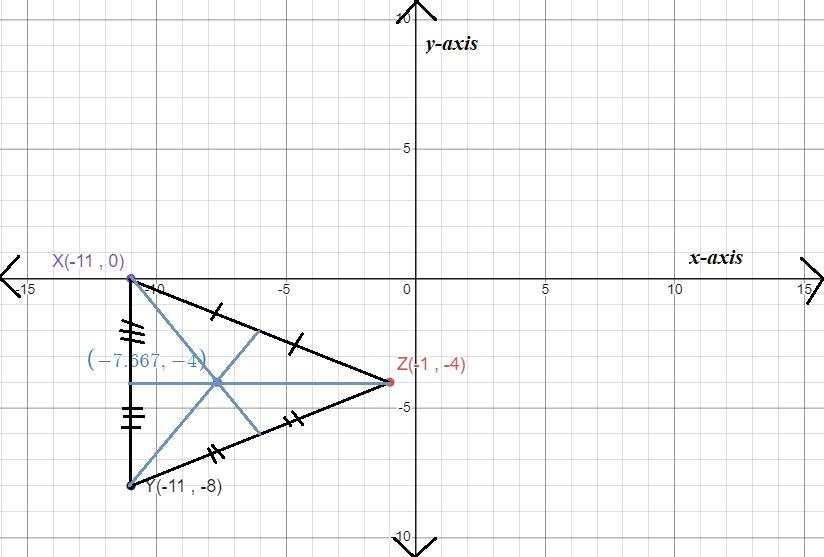
Find the coordinates of the centroid of the triangle with the given vertices. (Lesson 5-2)
X(-11,0), Y(-11,-8), Z(-1,-4)
Answers
The triangle with vertices located at X(-11 , 0), Y(-11 , -8), and Z(-1 , -4) has its centroid located at (-23/3 , -4).
The centroid of a triangle is the point inside the triangle where the three medians intersect. The median of a triangle is the line the connects the midpoint of a side and the opposite vertex.
To get the centroid of a triangle, use the formula given by:
C(x , y) = [(x1 + x2 + x3)/3 , (y1 + y2 + y3)/3]
where C is the centroid of the triangle located at (x , y)
x1, x2, and x3 are the x-coordinate of the vertices of the triangle
y1, y2, and y3 are the y-coordinate of the vertices of the triangle
Let Point 1(x1 , y1) = X(-11 , 0)
Point 2(x2 , y2) = Y(-11 , -8)
Point 3(x3 , y3) = Z(-1 , -4)
Plug in the values in the formula.
C(x , y) = [(x1 + x2 + x3)/3 , (y1 + y2 + y3)/3]
C(x ,y) = [(-11 + -11 + -1)/3 , (0 + -8 + -4)/3]
C(x ,y) = (-23/3 , -12/3)
C(x ,y) = (-23/3 , -4)
Learn more about centroid of triangle here: brainly.com/question/7644338
#SPJ4
Jim currently has $1,250 in his bank account and Sally has $1,400 in her bank account. Jim deposits $27.50 per week and Sally deposits $20 per week into her account. After how many weeks will they have the same amount of money?
Please help and thank you! :)
Answers
The number of weeks when Jim and Sally would have the same amount of money is 20 weeks.
The expression that can be used to represent the amount of money Jim would have in his account after x weeks is: $1,250 + 27.50x.
The expression that can be used to represent the amount of money Sally would have in his account after x weeks is: $1,400 + $20x.
In order to determine the number of weeks when they would have the same amount of money, the two expressions must be equal to each other.
$1,250 + 27.50x = $1,400 + $20x
Combine similar terms
$1,400 - $1,250 = $27.50x - $20x
150 = $7.50x
x = 150 / 7.50 = 20 weeks
A similar question was answered here: https://brainly.com/question/18491830?referrer=searchResults
3. A phone company set the following rate schedule for an m-minute
call from any of its pay phones.
c(m) =
=
0.70
0.70+ 0.24(m - 6)
0.70+ 0.24([m-6] + 1)
when m≤ 6
when m > 6 and m is an integer
when m> 6 and m is not an integer
a. What is the cost of a call that is under six minutes?
b. What is the cost of a 14-minute call?
c. What is the cost of a
1912-m
9-minute call?
Answers
The obtained answers for the given piecewise function are:
(a) The cost of a call that is under six minutes is 0.70 (m < 6)
(b) The cost of a 14-minute call is 2.62 (m > 6; m is an integer)
(c) The cost of a 9 1/2 minute call is 1.66 (m > 6; m is not an integer)
What is a piecewise function?A piecewise function is given by different functions at different intervals.
Calculation:It is given that,
phone company set the following rate schedule for an m-minute call from any of its pay phones.
C(m) = 0. 70 when m ≤ 6
= 0.70 + 0.24(m - 6) when m > 6 and m is an integer
= 0.70 + 0.24([m - 6] + 1) when m > 6 and m is not an integer
(a) The cost of a call that is under six minutes:
Since m < 6, the cost is C(m) = 0.76
Thus, the cost of a call that is under six minutes is 0.76
(b) The cost of a 14-minute call:
Since 14 > 6, the cost is C(m) = 0.70 + 0.24(m - 6) when m > 6 and m is an integer.
C(14) = 0.70 + 0.24(14 - 6)
= 0.70 + 0.24(8)
= 0.70 + 1.92
= 2.62
Thus, the cost of a 14-minute call is 2.62.
(c) The cost of a 9 1/2 minute call:
9 1/2 = 19/2 = 9.5
Since 9.5 > 6, the cost is C(m) = 0.70 + 0.24([m - 6] + 1) when m > 6 and m is not an integer.
C(9.5) = 0.70 + 0.24([9.5 - 6] + 1)
= 0.70 + 0.24([3.5] + 1)
Since we know that if [x] is a function then its domain is R and the range is Z(integer)
So, [3.5] = 3(is an integer)
Then,
C(9.5) = 0.70 + 0.24(3 + 1)
= 0.70 + 0.96
= 1.66
Therefore, the cost of a 9 1/2 minute call is 1.66.
Learn more about piecewise function here:
https://brainly.com/question/18859540
#SPJ9
can yall help me.....................

Answers
Answer:
14. False
15. True.
16. False
Step-by-step explanation:
14. 12+(9)<20
21<20 = False because 21 is >20 not less than 20
15. -3(8)<21
-24<21 = True because a negative number is always less than a positive number.
16. 12/4>5
3>5 = False because 3 is not greater than or equal to 5.
When each data value in one sample is matched with a corresponding data value in another sample, the samples are known as.
Answers
When each data value in one sample is matched with a corresponding data value in another sample, the samples are known as paired samples.
Paired samples are a type of experimental design in which two sets of data are compared for a given set of variables.
The term “paired” refers to the fact that each data point in one set corresponds to a specific data point in the other set.
Paired samples are a statistical method that is used to compare two groups of data.
Each set of data must be obtained from a single source.
A paired sample is where each observation in one group is matched with an observation in the other group.
This is a statistical technique that is frequently used in experimental research to measure the effect of a treatment on a particular group.
An example of a paired sample is when the same set of people are tested twice to determine the effect of a drug.
The first test is performed before the drug is administered, and the second test is performed after the drug has been administered.
The results of the two tests are then compared to determine the effect of the drug on the group of people.
Know more about paired samples here:
https://brainly.com/question/29979319
#SPJ11
Simplified awnser
1/2 a2 - 3 x b + 2c
Answers
The given expression is a simplified algebraic equation: (1/2) * a^2 - 3b + 2c. It represents a combination of variables a, b, and c with their respective coefficients.
What is an Algebraic Equation?Utilizing symbols and operations, an algebraic equation illustrates the equivalence or inequivalence of two expressions. These generated expressions may hold variables that have varying values.
The premise centered around calculus is to arrive at a solution by acquiring the correct value(s) of these variable(s), ultimately fulfilling the outlined specification in the problem. Algebraic equations can range from uncomplicated linear problems to elaborate polynomials and trigonometric functions.
Read more about algebraic equations here:
https://brainly.com/question/2164351
#SPJ1
Calculate the side lengths a and b to two decimal places.

Answers
Answer:
Can confirm, it’s a=16.23 and b=17.99
Complete the factorization of 3x2 – 5x 2. which two factors can be multiplied together to make this trinomial? (x – 2) (x – 1) (x 1) (3x – 2) (3x 2)
Answers
The factorization of the given polynomial is:
p(x) = (x - 2/3)*(x - 1) = (1/3)*(3x - 2)*(x - 1)
How to factorize the polynomial?
We have:
\(p(x) = 3x^2 - 5x + 2\)
First, we need to find the two roots for the equation, then we use Bhaskara's formula to get:
\(x = \frac{5 \pm \sqrt{5^2 - 4*3*2} }{2*3} \\\\x = \frac{5 \pm 1}{6}\)
So the two solutions are:
x = (5 + 1)/6 = 1
x = (5 - 1)/6 = 4/6 = 2/3
Then the polynomial can be written as:
p(x) = (x - 2/3)*(x - 1)
If you want to learn more about factorization
https://brainly.com/question/11579257
#SPJ4
Answer: (3x -2) and (x-1)
Step-by-step explanation:
Just took the test
2. Sixty percent of the students preferred raisins to banana chips. If there
(58)
were 95 students in all, how many preferred banana chips?
Answers
Answer:
536
try learning on cymath jc
convert 0.29 to a percentage
Answers
Answer:
0.29 as a percentage is the same as 29%
Step-by-step explanation:
it’s going to be 29% because you just pretend that there isn’t a 0. In front of the 29 and you have 29%.
The decimal number 0.29 is equivalent to 29% when expressed as a percentage.
Given decimal is 0.29.
To convert a decimal number to a percentage, multiply it by 100 and add the percentage symbol (%).
In this case, to convert 0.29 to a percentage
= 0.29 x 100
= 29
Therefore, 0.29 is equivalent to 29% as a percentage.
Learn more about percentage here:
https://brainly.com/question/24159063
#SPJ6
if my avg is a 96 and my final exam is a 75 which is 25% of my whole grade what will my final grade be
Answers
Step-by-step explanation:
That means the 96 is 75% of your grade
96 (.75) + 75 (.25) = 90.75 final grade
Please help quick! Thanks!

Answers
Answer:
69.9 (nice)
Step-by-step explanation:
To solve this, use the order of operations: PEMDAS (Parenthasis, exponents, Multiplication/Division, Addition/subtraction) In order.
1. Solve in the parenthasis, (2+3³). 3³ = 27, so 2+27 is 29. Plug in 29 to the equation: 5³-29×1.9
2. Next is exponents. 5³ has an exponent, which equals 125. Now you plug that into the equation to be 125-29×1.9
3. Now comes multiplication/division. In this case, it's multiplication. -29×1.9 . This equals -55.1, and you once again plug this into the equation to simplify which gives you 125 - 55.1
4. Last in the order of PEMDAS is addition/subtraction. The final simplification of the equation is 125 - 55.1 which is subtraction and this equals 69.9 (nice)
So in conclusion, your answer is 69.9 (nice)
the line joining A(a,3) to B(2,3) is perpendicular to the line joining C(10,1) to B. Find the value of a
Answers
The value of a in the given coordinates is 2.25.
Length of the lines joining the points
Apply Pythagoras theorem to determine the length of the lines.
|AC|² = |AB|² + |BC|²
(1 - 3)² + (10 - a)² = (3 - 3)² + (2 - a)² + (1 - 3)² + (10 - 2)²
4 + 100 - 20a + a² = 4 - 4a + a² + 4 + 64
104 - 20a + a² = 68 - 4a + a²
104 - 20a = 68 - 4a
104 - 68 = 20a - 4a
36 = 16a
a = 36/16
a = 2.25
Thus, the value of a in the given coordinates is 2.25.
Learn more about length of lines here: https://brainly.com/question/1597347
#SPJ1
What is an equation of the line that passes through the point (-2,-3) and is parallel to the line 5x+2y=14
Answers
Answer: y=-5/2x-8
Step-by-step explanation:
The equation of the line that passes through the point (-2,-3) and is parallel to the line 5x+2y=1 is
y = (-5/2)x - 8
What is an equation of a line?The equation of a line is given by:
y = mx + c
where m is the slope of the line and c is the y-intercept.
We have,
An equation of the line that passes through the point (-2,-3) and is parallel to the line 5x+2y=14.
The equation of a line can be written as:
y = mx + c _____(1)
The line 5x + 2y = 14 can be written in the form y = mx + c.
5x + 2y = 14
2y = -5x + 14
y = -5/2x + 7
m = -5/2 ____(2)
The equation of the line passes through the point (-2, -3) so,
From (1) and (2) we get,
y = mx + c
-3 = -5/2 x -2 + c
-3 = 5 + c
c = -3 - 5
c = -8 ____(3)
Now,
From (1) , (2), and (3) we get,
The equation of the line is
y = (-5/2)x - 8
Thus,
The equation of the line that passes through the point (-2,-3) and is parallel to the line 5x+2y=1 is
y = (-5/2)x - 8
Learn more about equation of a line here:
https://brainly.com/question/23087740
#SPJ5