4. THE LOV TEMPERATURES FOR A VEEK IN EDMONTON, ALBERTA ARE -15°C, -1200
-10°C, -12°C, -18°C, -20°C, AND_-25°C. WHAT IS THE MEAN LOV
TEMPERATURE FOR THE WEEK? SHOW YOUR WORK
Answers
Answer:
-16°C
Step-by-step explanation:
The lov temperatures for a week are :
-15°C, -12 , -10°C, -12°C, -18°C, -20°C, and -25°C.
We need to find the mean love temperature for the week.
Total no. of observations = 7
Mean = sum of observations/total no of observations
\(M=-\dfrac{15+12+10+12+18+20+25}{7}\\\\M=-16^{\circ} C\)
So, the mean temperature is -16°C.
Related Questions
Henry opens a savings account that has a 4.5% annual interest
rate. After 18 months, he receives $75,000. How much did he invest?
Show all work
Answers
Henry opens a savings account with an annual interest rate of 4.5 percent. After a year, he gets $75,000 in payment. He made a deposit into the savings account of $72,831.68.
Here are the steps on how to calculate the amount Henry invested:
Convert the annual interest rate to a monthly rate.
\(\begin{equation}4.5\% \div 12 = 0.375\%\end{equation}\)
Calculate the number of years.
\(\begin{equation}\frac{18 \text{ months}}{12 \text{ months/year}} = 1.5 \text{ years}\end{equation}\)
Use the compound interest formula to calculate the amount Henry invested.
\(\begin{equation}FV = PV * (1 + r)^t\end{equation}\)
where:
FV is the future value ($75,000)
PV is the present value (unknown)
r is the interest rate (0.375%)
t is the number of years (1.5 years)
\(\begin{equation}\$75,000 = PV \cdot (1 + 0.00375)^{1.5}\end{equation}\)
\$75,000 = PV * 1.0297
\(\begin{equation}PV = \frac{\$75,000}{1.0297}\end{equation}\)
PV = \$72,831.68
Therefore, Henry invested \$72,831.68 in the savings account.
To know more about the annual interest rate refer here :
https://brainly.com/question/20631001#
#SPJ11
Write an equation in slope intercept form with the given information Slope is -2 and y- intercept is 3.
Answers
Answer:
y = -2x + 3
Step-by-step explanation:
Ya I just put it in the format
Answer:
y = -2x + 3
Step-by-step explanation:
Slope-Intercept Form: y = mx + b
Slope: -2
Y-Intercept: 3
y = -2x + 3
solve for h
24 = 3(h-5)
Answers
Answer:
H = 13
Step-by-step explanation:
==>24 = 3(h-5)
==> 3(h - 5)=24
==> 3h - 15 =24
==> 3h = 24 + 15
==> 3h = 39
==> \(h = \frac{39}{3} \)
==> h = 13
write the formula for the conjugate base for each of the following weak acids. (a) hc2h3o2
Answers
The conjugate base of the weak acid hc2h3o2 (acetic acid) can be determined by removing a proton (H+) from the acid molecule. The formula for the conjugate base is C2H3O2- (acetate ion).
The formula for acetic acid (hc2h3o2) suggests that it consists of the elements hydrogen (H), carbon (C), and oxygen (O). To determine the formula of its conjugate base, we remove a proton (H+) from the acid molecule. Removing a proton results in the formation of an anion, which has a negative charge to maintain overall charge neutrality.
The removal of a proton from hc2h3o2 leads to the formation of the acetate ion, which has a formula of C2H3O2-. The C2H3O2- ion is referred to as the conjugate base of acetic acid.
In summary, the formula for the conjugate base of the weak acid hc2h3o2 (acetic acid) is C2H3O2- (acetate ion).
To learn more about acetate ion, click here: brainly.com/question/30030979
#SPJ11
What is the value of the expression below?
(8 + 1/8) divided by (2.5 + 3/4)
Answers
Answer:
0.64615384615
Step-by-step explanation:
(2.5 + 2.75)/(8 + 1/8)
5.25/8 1/8
1/8 = 0.125
5.25/8.125 =
=0.64615384615
Hope this helps! I might be wrong
Answer: A (2.5)
Step-by-step explanation: got it right on edge 2021
.A system consists of five identical components connected in series as shown:
A system consists of five identical components con
As soon as one components fails, the entire system will fail. Suppose each component has a lifetime that is exponentially distributed with ? = 0.01 and that components fail independently of one another. Define eventsAi = {ith component lasts at least t hours}, i = 1, . . . , 5, so that the Ais are independent events. Let X = the time at which the system fails
Answers
The time at which the system fails, denoted by X, is the minimum of the lifetimes of the five components.
In this system, each component has a lifetime that follows an exponential distribution with a parameter λ = 0.01. The exponential distribution is commonly used to model the time until an event occurs in a system with a constant failure rate.
The probability that a component lasts at least t hours is given by P(Ai) = e^(-λt), where Ai is the event that the ith component lasts at least t hours.
Since the components fail independently of one another, the probability that all five components last at least t hours is the product of their individual probabilities: P(A1 ∩ A2 ∩ A3 ∩ A4 ∩ A5) = e^(-λt)^5 = e^(-5λt).
Now, let X be the time at which the system fails, which is the minimum of the lifetimes of the five components. Since X is the minimum, we can write X = min(T1, T2, T3, T4, T5), where Ti represents the lifetime of the ith component.
The probability distribution of X can be obtained by considering the complement event. The complement of X > t is that all five components last at least t hours, which is P(X > t) = P(A1 ∩ A2 ∩ A3 ∩ A4 ∩ A5) = e^(-5λt).
Therefore, the time at which the system fails, X, follows an exponential distribution with a parameter of 5λ = 0.05. This means that the system has a constant failure rate of 0.05 and the probability density function (pdf) of X is given by f(x) = 0.05 * e^(-0.05x).
Visit here to learn more about probability:
brainly.com/question/31828911
#SPJ11
The population on a certain island increased from 1500 in 2000 to 1577 in 2001 a. Determine the growth rate b. Write a general equation for the popolation p(t) c. Estimate the population in 2010 d. How many years will it take for the population to double?
Answers
Therefore, it will take approximately 13.7 years for the population to double.
a. To determine the growth rate, you need to calculate the percentage increase in population. The formula for growth rate is:
Growth Rate = (New Value - Old Value) / Old Value * 100
Using the given values, we have:
Growth Rate = (1577 - 1500) / 1500 * 100
Growth Rate = 77 / 1500 * 100
Growth Rate ≈ 5.13%
b. To write a general equation for the population, you can use the formula:
p(t) = p(0) * (1 + r/100)^t
where p(t) is the population at time t, p(0) is the initial population, r is the growth rate, and t is the number of years.
c. To estimate the population in 2010, we need to find the population at time t = 2010 - 2000 = 10 years. Using the general equation from part b, and substituting the given values:
p(10) = 1500 * (1 + 5.13/100)^10
p(10) ≈ 1500 * (1.0513)^10
p(10) ≈ 1500 * 1.6436
p(10) ≈ 2465.4
Therefore, the estimated population in 2010 is approximately 2465.
d. To find out how many years it will take for the population to double, we need to solve the equation:
2 * p(0) = p(0) * (1 + r/100)^t
Simplifying the equation, we have:
2 = (1 + r/100)^t
Taking the logarithm of both sides, we get:
log(2) = t * log(1 + r/100)
Finally, solving for t, we have:
t = log(2) / log(1 + r/100)
Substituting the growth rate from part a, we have:
t = log(2) / log(1 + 5.13/100)
t ≈ log(2) / log(1.0513)
t ≈ 13.7 years
Therefore, it will take approximately 13.7 years for the population to double.
To know more about population visit :
https://brainly.com/question/19169926
#SPJ11
problem 5 (30 points, each 10 points). in a chemical plant, 24 holding tanks are used for final product storage. four tanks are selected at random and without replacement. suppose that four of the tanks contain material in which the viscosity exceeds the customer requirements. 1. what is the probability that exactly one tank in the sample contains high-viscosity material? 2. what is the probability that at least one tank in the sample contains high-viscosity material? 3. in addition to the four tanks with high-viscosity levels, four different tanks contain material with high impurities. what is the probability that exactly one tank in the sample contains high-viscosity material and exactly one tank in the sample contains material with high impurities?
Answers
1. The probability of selecting exactly one tank with high-viscosity material is 0.
2. The probability of selecting at least one tank with high-viscosity material is 1.
3. The probability of selecting exactly one tank with high-viscosity material and exactly one tank with high impurities is 0.25.
1. The probability of selecting exactly one tank with high-viscosity material is calculated by the binomial distribution formula, P(X = n) = (nCx)p^x(1-p)^n-x, where n is the number of trials, x is the number of successes, and p is the probability of success. In this case, n = 4, x = 1, and p = 24/24 = 1. Therefore, P(X = 1) = (4C1)1^1(1-1)^4-1 = 0.
2. The probability of selecting at least one tank with high-viscosity material is calculated by the complement rule, P(X > 0) = 1 - P(X = 0). In this case, P(X > 0) = 1 - (4C0)1^0(1-1)^4-0 = 1.
3. The probability of selecting exactly one tank with high-viscosity material and exactly one tank with high impurities is calculated by the binomial distribution formula, P(X = n) = (nCx)p^x(1-p)^n-x, where n is the number of trials, x is the number of successes, and p is the probability of success. In this case, n = 8, x = 2, and p = 24/24 = 1. Therefore, P(X = 2) = (8C2)1^2(1-1)^8-2 = 0.25.
Learn more about probability here:
https://brainly.com/question/14206287
#SPJ4
Pls help with letter I and letter H pls be quick hurrry asap pls be real answer this is 50% of my grade

Answers
Answer:
h. 182.4
l. 2.5
Step-by-step explanation:
For h, cross multiply 12 and 15.2 we get 182.4
For l, Keep 1/2 to other side and we multiply 5 and 1/2.
Hope it helps :)
Answer:
H) 182.4 I) 5/2
Step-by-step explanation:
See attached - hope this helps!

Plz help, will give brainliest.


Answers
Answer:
1) X = 10 Therefore, 10 + 2 + 10 = 22.
2) B = 2 Therefore, 15 = 8(2) - 5 + 2(2)
3) B = -0.9 Therefore, -10 + 4(3(-0.9) + 10) = 19.
A doctor advises a patient not to consume more than 8.5 × 10−2 kg of sugar per day. Coca cola
contains 110 g/L sugar. How many 12 oz cans of Coca cola can the patient consume? Show your work.
Answers
The patient can consume approximately 2 cans of 12 oz Coca Cola without exceeding the advised sugar limit.
To determine the number of 12 oz cans of Coca Cola the patient can consume, we need to convert the sugar limit provided by the doctor into grams and then calculate the amount of sugar in a 12 oz can of Coca Cola.
Provided:
Sugar limit: 8.5 × 10^(-2) kg
Coca Cola sugar content: 110 g/L
Volume of a 12 oz can: 12 oz (which is approximately 355 mL)
First, let's convert the sugar limit from kilograms to grams:
Sugar limit = 8.5 × 10^(-2) kg = 8.5 × 10^(-2) kg × 1000 g/kg = 85 g
Next, we need to calculate the amount of sugar in a 12 oz can of Coca Cola:
Volume of a 12 oz can = 355 mL = 355/1000 L = 0.355 L
Amount of sugar in a 12 oz can of Coca Cola = 110 g/L × 0.355 L = 39.05 g
Now, we can determine the number of cans the patient can consume by dividing the sugar limit by the amount of sugar in a can:
Number of cans = Sugar limit / Amount of sugar in a can
Number of cans = 85 g / 39.05 g ≈ 2.18
Since the number of cans cannot be fractional, the patient should limit their consumption to 2 cans of Coca Cola.
To know more about sugar limit refer here:
https://brainly.com/question/30510739#
#SPJ11
(-4,-2) (0,2) (-2,1) find the domain and range and can you tell me if it’s a function ?? PLS HELPPP
Answers
Answer:
domain means -4,0,-2 and range is -2,2,1
In the given figure ABCD, prove that
angleBCD= angleBAD+ angle ABC+angle ADC.
[Hint: Join A and C then extended AC to the point E]

Answers
We have proved that Angle BCD is equal to angle BAD plus angle ABC plus angle ADC, as required.
To prove that angle BCD is equal to angle BAD plus angle ABC plus angle ADC, we can use the following steps:
Step 1: Join points A and C with a line segment. Let's label the point where AC intersects with line segment BD as point E.
Step 2: Since line segment AC is drawn, we can consider triangle ABC and triangle ADC separately.
Step 3: In triangle ABC, we have angle B + angle ABC + angle BCA = 180 degrees (due to the sum of angles in a triangle).
Step 4: In triangle ADC, we have angle D + angle ADC + angle CDA = 180 degrees.
Step 5: From steps 3 and 4, we can deduce that angle B + angle ABC + angle BCA + angle D + angle ADC + angle CDA = 360 degrees (by adding the equations from steps 3 and 4).
Step 6: Consider quadrilateral ABED. The sum of angles in a quadrilateral is 360 degrees.
Step 7: In quadrilateral ABED, we have angle BAD + angle ABC + angle BCD + angle CDA = 360 degrees.
Step 8: Comparing steps 5 and 7, we can conclude that angle B + angle BCD + angle D = angle BAD + angle ABC + angle ADC.
Step 9: Rearranging step 8, we get angle BCD = angle BAD + angle ABC + angle ADC.
Therefore, we have proved that angle BCD is equal to angle BAD plus angle ABC plus angle ADC, as required.
For more questions on Angle .
https://brainly.com/question/31615777
#SPJ8
Given: Quadrilateral \(\displaystyle\sf ABCD\)
To prove: \(\displaystyle\sf \angle BCD = \angle BAD + \angle ABC + \angle ADC\)
Proof:
1. Draw segment \(\displaystyle\sf AC\) and extend it to point \(\displaystyle\sf E\).
2. Consider triangle \(\displaystyle\sf ACD\) and triangle \(\displaystyle\sf BCE\).
3. In triangle \(\displaystyle\sf ACD\):
- \(\displaystyle\sf \angle ACD = \angle BAD + \angle ADC\) (Angles of a triangle add up to \(\displaystyle\sf 180^\circ\)).4. In triangle \(\displaystyle\sf BCE\):
- \(\displaystyle\sf \angle BCE = \angle BAD + \angle ABC\) (Angles of a triangle add up to \(\displaystyle\sf 180^\circ\)).5. Since \(\displaystyle\sf \angle BCE\) and \(\displaystyle\sf \angle BCD\) are corresponding angles formed by transversal \(\displaystyle\sf BE\):
- \(\displaystyle\sf \angle BCE = \angle BCD\).6. Combining the equations from steps 3 and 4:
- \(\displaystyle\sf \angle BCD = \angle ACD = \angle BAD + \angle ADC\). - \(\displaystyle\sf \angle BCD = \angle BCE = \angle BAD + \angle ABC + \angle ADC\).Therefore, we have proven that in quadrilateral \(\displaystyle\sf ABCD\), \(\displaystyle\sf \angle BCD = \angle BAD + \angle ABC + \angle ADC\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
prove that (1 2 3 ··· n) 2 = 1 3 2 3 3 3 ··· n 3 for every n ∈ n.
Answers
The equation holds for k, it also holds for k + 1. we have proven that (1 2 3 ··· n)² = 1 3 2 3 3 3 ··· n³ for every n ∈ ℕ.
To prove that (1 2 3 ··· n)² = 1 3 2 3 3 3 ··· n³ for every n ∈ ℕ, we will use mathematical induction.
Base case:
Let's start by verifying the equation for the base case when n = 1:
(1)² = 1³
The base case holds true.
Inductive step:
Next, we assume that the equation holds for some positive integer k, where k ≥ 1. That is, we assume that (1 2 3 ··· k)² = 1 3 2 3 3 3 ··· k³.
Now, we need to show that the equation holds for k + 1, i.e., we need to prove that ((1 2 3 ··· k) (k+1))² = 1 3 2 3 3 3 ··· k³ (k+1)³.
Expanding the left-hand side of the equation:
((1 2 3 ··· k) (k+1))² = (1 2 3 ··· k)² (k+1)²
Using the assumption that (1 2 3 ··· k)² = 1 3 2 3 3 3 ··· k³, we can rewrite the left-hand side as:
(1 3 2 3 3 3 ··· k³) (k+1)²
Now, let's analyze the right-hand side of the equation:
1 3 2 3 3 3 ··· k³ (k+1)³ = 1 3 2 3 3 3 ··· k³ (k³ + 3k² + 3k + 1)
We can see that the right-hand side consists of the terms from 1³ to k³, followed by (k+1)³, which is equivalent to (k³ + 3k² + 3k + 1).
Comparing the expanded left-hand side and the right-hand side, we notice that they are equivalent:
(1 3 2 3 3 3 ··· k³) (k+1)² = 1 3 2 3 3 3 ··· k³ (k³ + 3k² + 3k + 1)
Therefore, we have shown that if the equation holds for k, it also holds for k + 1.
Since the base case holds true and we have shown that if the equation holds for k, it also holds for k + 1, we can conclude that the equation holds for all positive integers n.
Hence, we have proven that (1 2 3 ··· n)² = 1 3 2 3 3 3 ··· n³ for every n ∈ ℕ.
Learn more about equation here
https://brainly.com/question/29174899
#SPJ11
What are the coordinates of this point?
PLLEASS ANSWER IM GVING BRAINLIEST
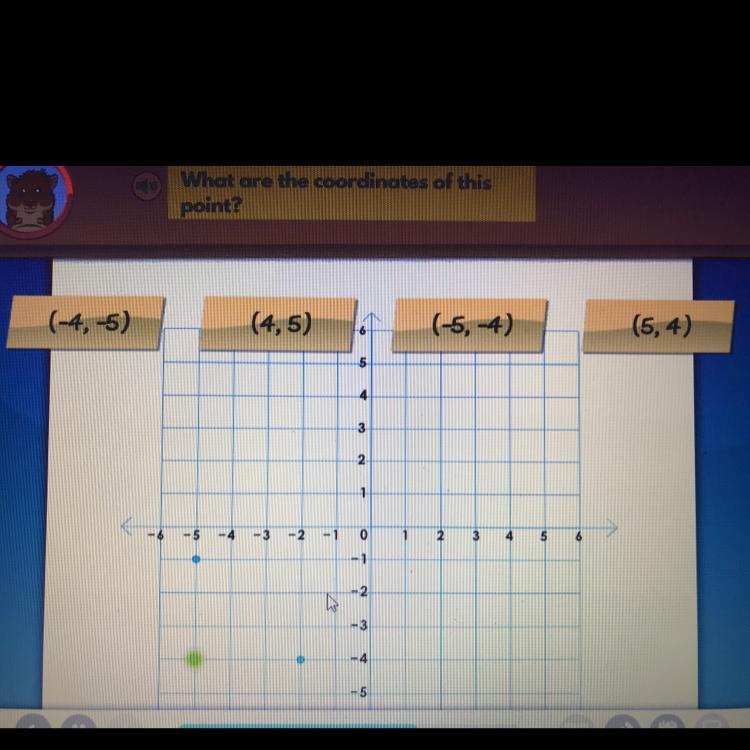
Answers
Answer:
Step-by-step explanation:
they are (-5,-4) hope this helped
Answer: the answer is (-4,-5)
Step-by-step explanation: hopefully that helps
Find the volume of a right circular cone that has a height of 18.8 m and a base with a
radius of 19.3 m. Round your answer to the nearest tenth of a cubic meter.
Answers
Step-by-step explanation:
Height of the right circular cone = 18.8 metres
And base is 19.3 metres
Volume of the right circular cylinder is given by,
= πr²h
= 3.14 × (19.3)² × 18.8
= 21999.98(approx.) cubic metre
Rounding off nearest tenth
= 21999 cubic metres
The volume of the right circular cone is 280,199.5 m³
What is a right circular cone?
'A right circular cone is a cone where the axis of the cone is the line meeting the vertex to the midpoint of the circular base.'
According to the given problem,
Height = 18.8 m
Radius = 19.3 m
Volume of right circular cone = \(\frac{\pi r^{2}h }{3}\)
= \(\frac{\pi * 19.3^{2} * 18.8}{3}\)
= 280199.499 m³
= 280199.5 m³
Hence, we can conclude that the volume of the right circular cone is 280199.5 m³.
Learn more about right circular cone here: https://brainly.com/question/16655425
#SPJ2
Six times the sum of half a number x and 12 is 30
Answers
Answer:
-14
Step-by-step explanation:
Translate the words to an equation
6(\(\frac{x}{2}\) + 12) = 30
Divide both sides by 6
\(\frac{x}{2}\) + 12 = 5
Multiply both sides by 2
x + 24 = 10
Subtract 24 from both sides
x = -14
3x-2y=12 and 3x+5y=33
Answers
Answer:
x=6, y=3. (6, 3).
Step-by-step explanation:
3x-2y=12
3x+5y=33
--------------
-3x+2y=-12
3x+5y=33
-------------------
7y=21
y=21/7=3
3x-2(3)=12
3x-6=12
3x=12+6
3x=18
x=18/3=6
write a polynomial given the zeros of 0 (multiplicity 2), 1
Answers
Answer:
\(\displaystyle{P(x)=x^3-x^2}\)
Step-by-step explanation:
Given the zeros of 0, 0, 1. We can write the polynomial in form of x-intersects:
\(\displaystyle{P(x) = (x-x_1)(x-x_2)(x-x_3)}\)
Hence:
\(\displaystyle{P(x)=(x-0)(x-0)(x-1)}\)
Which can be simplified to:
\(\displaystyle{P(x)=x\cdot x \cdot (x-1)}\\\\\displaystyle{P(x)=x^2(x-1)}\)
Convert to the standard form by distributing x²:
\(\displaystyle{P(x)=x^2\cdot x - x^2 \cdot 1}\\\\\displaystyle{P(x)=x^3-x^2}\)
Find the volume of this object.
Use 3 for. Volume of a Cylinder
V=Tr2h
4ft
3ft
Volume of a
Rectangular Prism
V = lwh
4ft
//4ft
V~[?]ft?
7 ft
Answers
We are expected to find the volume of the item which contains a cylinder and a cone = The volume of the item is 108 in³
The volume of a cylinder = πr²h
π = 3
r =/2 = 4 in/2 = 2 in
h = 8 in
The volume of a cylinder = πr²h
= 3 × (2 in)² × 8 in
= 3 × 4 in² × 8 in
= 96 in³
The volume of a cone = πr²h/3
= (3 × (2 in)² × 3 in)/3
= (3 × 4 in² × 3 in)/3
= 36 in³/3
= 12 in³
The volume of the item can be found by adding the volume of the cylinder and the volume of the cone
Total volume = Volume of a cylinder + Volume of a cone
= 96 in³ + 12 in³
= 108 in³
to know more about the volume of the cylinder click here:
https://brainly.com/question/6204273
#SPJ4
required parameters. (e) Write the complex number 5+2i in the exponential form Aeie. (f) A spring-mass system has a natural period of 0.31 second. Calculate the new period if the spring constant is increased by 60%.
Answers
(e) The complex number 5+2i in exponential form is (\sqrt{29}e^{i\text{tan}^{-1}\left(\frac{2}{5}\right)}\).
(f) The new period is \(0.31\sqrt{\frac{m}{1.6k}}\) when the spring constant is increased by 60%.
(e) To convert a complex number to exponential form, we need to determine its magnitude and argument. For the complex number 5+2i, the magnitude is given by the formula \(A = \sqrt{{\text{Re}}^2 + {\text{Im}}^2}\) where Re and Im represent the real and imaginary parts, respectively. In this case, the magnitude is \(\sqrt{5^2 + 2^2} = \sqrt{29}\).
The argument, \(\theta\), can be found using the formula \(\theta = \text{tan}^{-1}\left(\frac{{\text{Im}}}{{\text{Re}}}\right)\). For 5+2i, the argument is \(\text{tan}^{-1}\left(\frac{2}{5}\right)\).
Thus, the complex number 5+2i in exponential form is \(Ae^{i\theta} = \sqrt{29}e^{i\text{tan}^{-1}\left(\frac{2}{5}\right)}\).
(f) The period of a spring-mass system is determined by the mass and the spring constant. If the spring constant is increased by 60%, we can calculate the new period using the formula \(T' = T\sqrt{\frac{m}{k'}}\).
Given the original period \(T = 0.31\) seconds and an increase in the spring constant by 60%, we have \(k' = 1.6k\) where \(k\) is the original spring constant.
Substituting the values into the formula, the new period is \(T' = 0.31\sqrt{\frac{m}{1.6k}}\).
Increasing the spring constant causes the spring to become stiffer, resulting in a shorter period. The new period, \(T'\), will be less than the original period \(T\) due to the increased stiffness of the spring.
Learn more about Exponential form click here :brainly.com/question/23275698
#SPJ11
Given the two rectangles below. Find the area of the shaded region. 2 4 10 2

Answers
help with these two pages




Answers
A square is a quadrilateral with four equal sides and four equal angles that is a regular quadrilateral. The square's angles are at a straight angle or 90 degrees.
Explain about the square?Area of a square is measured in square units. The area of a square equals d22 square units when the diagonal, d, is known. For instance, a square with sides that are each 8 feet long is 8 8 or 64 square feet in area (ft2)
A square is a common polygon with four equal sides and angles that are each 90 degrees in length.
A square is a four-sided polygon with sides that are all the same length and angles that are all exactly 90 degrees. The square's shape ensures that both parts are symmetrical if it is divided down the middle by a plane. Then, each half of the square seems to be a rectangle with diagonal sides.
To learn more about square refer to:
https://brainly.com/question/25092270
#SPJ1
Allison is evaluating the expression -5-(-2) using integer tiles. She begins with 5 negative tiles as shown
VX
What should Allison do next to find the value of the expression?
remove 2 negative tiles
remove 3 negative tiles
add 2 negative tiles
Add 7 negative tiles
Answers
Answer:
its B. -3
Step-by-step explanation:
Remove 3 negative tiles .
Can I get brainliest??????
Answer:
Step-by-step explanation:
its b
Andre rode his bike at a constant speed. He rode 1 mile in 5 minutes. Which of these equations represents the amount of time t (in minutes) that it takes him to ride a distance of d miles?
Answers
Answer:
.20 per minute.If you dives 1 mile by 5 min u will get .20
The U.S. Department of Education reported that for the past seven years:4,0335,6426,4077,7538,71911,15411,121people received bachelor's degrees in JournalismWhat is the arithmetic mean annual number receiving this degree
Answers
The arithmetic mean annual number of people receiving a bachelor's degree in Journalism is about 7,833.
To find the arithmetic mean annual number of people receiving a bachelor's degree in Journalism over the past seven years, we need to calculate the average of the given data set.
The data set representing the number of people receiving bachelor's degrees in Journalism for each of the seven years is:
4,033
5,642
6,407
7,753
8,719
11,154
11,121
To find the mean, we sum up all the values and divide by the total number of years (in this case, seven).
Mean = (4,033 + 5,642 + 6,407 + 7,753 + 8,719 + 11,154 + 11,121) / 7
= 54,829 / 7
≈ 7,832.714
Rounding to the nearest whole number, the arithmetic mean annual number of people receiving a bachelor's degree in Journalism over the past seven years is approximately 7,833.
Therefore, the arithmetic mean annual number of people receiving a bachelor's degree in Journalism is about 7,833.
Learn more about arithmetic here:
https://brainly.com/question/16415816
#SPJ11
What is the standard form of the number 4.356 x 10^4?
Answers
Answer:
43,560
Step-by-step explanation:
First, let's solve the exponent value. 10 to the power 4 means that there will be 4 zeros, so the number is 10,000.
We have to multiply this by 4.356. Remember 10,000 has 4 zeros! So to make this easier, let's just move the decimal point right 4 places to get 43,560.
Therefore, the answer is 43,560.
Hope I helped!!!
find all points in the plane with abscissa equal to 3 whose
distance to the point (-2,-1) is 13.
Answers
The two points in the plane with abscissa equal to 3 and a distance of 13 units away from the point (-2, -1) are (3, 11) and (3, -13).
All points in the plane with abscissa equal to 3 that are a distance of 13 units away from the point (-2, -1), we can use the distance formula.
Let's denote the y-coordinate of the point as y.
The distance between two points (x₁, y₁) and (x₂, y₂) is given by the formula:
distance = √((x₂ - x₁)² + (y₂ - y₁)²)
In this case, we have:
x₁ = 3 (abscissa)
y₁ = y (ordinate)
x₂ = -2
y₂ = -1
Plugging in these values into the distance formula:
13 = √((-2 - 3)² + (-1 - y)²)
Simplifying:
169 = (5)² + (-1 - y)²
169 = 25 + (1 + 2y + y²)
169 = 25 + 1 + 2y + y²
Rearranging the equation:
y² + 2y - 143 = 0
Now we have a quadratic equation. We can solve it by factoring, completing the square, or using the quadratic formula.
Factoring this quadratic equation is not straightforward, so let's use the quadratic formula:
y = (-b ± √(b² - 4ac)) / (2a)
For our equation, a = 1, b = 2, and c = -143.
Plugging in these values into the quadratic formula:
y = (-2 ± √(2² - 4(1)(-143))) / (2(1))
Simplifying:
y = (-2 ± √(4 + 572)) / 2
y = (-2 ± √(576)) / 2
y = (-2 ± 24) / 2
We have two possible values for y:
y₁ = (-2 + 24) / 2 = 22 / 2 = 11
y₂ = (-2 - 24) / 2 = -26 / 2 = -13
Therefore, the two points in the plane with abscissa equal to 3 and a distance of 13 units away from the point (-2, -1) are (3, 11) and (3, -13).
To know more about abscissa click here :
https://brainly.com/question/30916214
#SPJ4
PLEASE PLEASE HELP ME !!!i need to solve this doing the zero product property

Answers
x=7 and x=-5
What is the slope shown below?

Answers
Answer:
5/8
Step-by-step explanation:
Slope = rise/run
In this problem:
rise = 5
run = 8
Therefore, Slope = 5/8