4. What information do you need to classify quadrilateral EFGH as
a square?
Answers
opposite sides are congruent.
adjacent angles are supplementary.
the diagonals bisect each other.
if a quadrilateral has four congruent sides and four right angles, then it is a square.
Answer:
i think area of quad=area of square(equal sides)
Related Questions
Which expression is equival 81 1/3?
Answers
Answer: 3^3 Square root 3
Step-by-step explanation:
Which of the following symbols could correctly finish the statement. Select all that apply.
-3 ___ 0
>
≤
=
≠
≥
Answers
Answer: >
Step-by-step explanation:
Answer:
≤ ≠
Step-by-step explanation:
-3 is less than 0
What would be the slope of the positions (3,3) and (4,5)
Answers
Answer:
m = 2
Step-by-step explanation:
Slope Formula: \(m=\frac{y_2-y_1}{x_2-x_1}\)
Simply plug our coordinates into the slope formula and solve for m:
m = (5 - 3)/(4 - 3)
m = 2/1
m = 2
Answer:
2Step-by-step explanation:
Let the points be A and B
A( 3 , 3 ) -----> ( x1 , y1 )
B(4 , 5 ) ------>( x2 , y2 )
Now,
finding the slope,
Slope =\( \frac{y2 - y1}{x2 - x1} \)
\( = \frac{5 - 3}{4 - 3} \)
\( = \frac{2}{1} \)
\( = 2\)
Hope this helps...
Good luck on your assignment..
Let p be the probability that, in the process of repeatedly flipping a fair coin, one will encounter a run of 5 heads before one encounters a run of 2 tails. Given that p can be written in the form m/n where m and n are relatively prime positive integers, find m+n.
Answers
The value of m+n is 37.
Probability is a measure of the likelihood that an event will occur or the likelihood that something will happen. The range for probability varies from 0 to 1.
Let A signify the flipping of the head, and let B signify the flipping of the tail. The event ends when we get 5 heads or 2 tails while flipping.
Then, the outcomes are given by AAAAA, BAAAAA, BB, ABB, AABB, AAABB, AAAABB. The probability of getting a head is 1/2 and a tail is 1/2. The probability of the possible outcomes is 1/32, 1/64, 1/4, 1/8, 1/16, 1/32, and 1/64.
The outcomes with five heads are AAAAA and BAAAAA. The sum of the probabilities of getting 5 heads is,
\(\begin{aligned}\frac{1}{32}+\frac{1}{64}&=\frac{2+1}{64}\\&=\frac{3}{64}\end{aligned}\)
And, the sum of all the outcomes is, \(\begin{aligned}\frac{1}{32 }+ \frac{1}{64}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}&=\frac{2+1+16+8+4+2+1}{64}\\&=\frac{34}{64}\end{aligned}\)
Let p is the probability that a run of 5 heads will occur before a run of 2 tails. The desired probability p is,
\(\begin{aligned}p&=\frac{\text{number of event}}{\text{total outcome}}\\&=\frac{\frac{3}{64}}{\frac{34}{64}}\\&=\frac{3}{34}\end{aligned}\)
Given, p is of the form m/n. So, m is 3 and n is 34. Then, m+n=3+34=37.
The answer is 37.
To know more about coin probability:
https://brainly.com/question/5495713
#SPJ4
What is the answer to the question??

Answers
Answer:you need to show the diagram in order for me to
Step-by-step explanation:
7th grade math help me plzzz

Answers
Answer:
\(b. \: \frac{1}{10} ......series\)
Una pregunta sobre notación científica. ¿Cómo se pasaría un numero entre 1 y 9,999... a notación científica? Por ejemplo el 3,125007 ¿Qué se hace en ese caso, es posible elevar el 10 a la cero?
Answers
3.125007 in scientific notation would be written as 0.03125007 x 10^2.
How to solve thisTo convert a number to scientific notation, you first determine the exponent to which 10 must be raised to make the number equal to or greater than 1 but less than 10.
In the case of 3.125007, you would multiply it by 10 and raise it to a power such that it becomes a number between 1 and 10.
In this case, you would multiply by 10 raised to the power of -2:
3.125007 * 10^-2 = 0.03125007
So, 3.125007 in scientific notation would be written as 0.03125007 x 10^2.
Note: It is not possible to raise 10 to zero, as 10 to the power of 0 is always equal to 1.
Read more about scientific notations here:
https://brainly.com/question/5756316
#SPJ1
The question in English is:
"How would you convert a number between 1 and 9,999... to scientific notation? For example, 3.125007. What is done in this case, is it possible to raise 10 to zero?"
Which statement is correct?
A)The Interquartile Range (IQR) for the Chess Club is equal to the IQR for the Checkers Club.
B)The 3rd Quartile ages for the Chess Club is equal to the 3rd Quartile ages for the Checkers Club.
C)The Median age for the Chess Club members is twice that of the Median age for the Checkers Club members.
D)The Range of the Chess Club members is equal to the Range for the Checkers Club members.

Answers
Answer:
B
Step-by-step explanation:
A new is being built in Safety Harbor. The perimeter of the rectangular playing field is 582 yards. The length of the field is 4 yards less than quadruple the width. What are the dimensions of the playing field?
Answers
The dimensions of the rectangular field are given as follows:
Length: 232 yards.Width: 59 yards.How to obtain the perimeter of a rectangle?The perimeter of a rectangle is given by twice the sum of the length and the width of the rectangle, as follows:
P = 2(l + w).
For this problem, the perimeter is of 582 yards, hence:
2(l + w) = 582
l + w = 291.
The length of the field is 4 yards less than quadruple the width, hence:
l = 4w - 4.
Then the width is obtained as follows:
4w - 4 + w = 295
5w = 295
w = 295/5
w = 59.
The length is obtained as follows:
l = 4 x 59 - 4
l = 232 yards.
More can be learned about the perimeter of a rectangle at https://brainly.com/question/24571594
#SPJ1
A local coffee house surveyed 317 customers regarding their preference of chocolate chip or cranberry walnut scones . 150 customers prefer the Cranberry Walnut Scones . 81 customers who responded were males and prefer the Chocolate Chip Scones . 172 female customers responded . Find the probability that a customer chosen at random will be a male or prefer the Chocolate Chip Scones .
1. 25.6%
2. 24.1%
3. 72.9%
4. 98.4%
Answers
Answer:
3. 72.9%
Step-by-step explanation:
Let's call M the event that the customer is male and C the event that the customer prefer chocolate chips Scones.
So, the probability P(M∪C) that a customer chosen at random will be a male or prefer the Chocolate Chip Scones is calculated as:
P(M∪C) = P(M) + P(C) - P(M∩C)
Then, there are 145 males (317 customer - 172 females = 145 males), so the probability that the customer is a males is:
P(M) = 145/317 = 0.4574
There are 167 customers that prefer chocolate chips Scones ( 317 customers - 150 customers that prefer the Cranberry Walnut Scones = 167), so the probability that a customer prefer chocolate chips Scones is:
P(C) = 167/317 = 0.5268
Finally, 81 customers were males and prefer the Chocolate Chip Scones, so the probability that a customer will be a male and prefer chocolate chip scones is:
P(M∩C) = 81/317 = 0.2555
Therefore, P(M∪C) is equal to:
P(M∪C) = 0.4574 + 0.5268 - 0.2555
P(M∪C) = 0.7287
P(M∪C) = 72.9%
Answer:
3. 72.9%
Step-by-step explanation:
A probability is the number of desired outcomes divided by the number of total outcomes.
Desired outcomes:
Male or prefers the Chocolate Chip Scones. That is, males and females who prefer the Chocolate Chip Scones.
There are 172 female customers and 317-172 = 145 male customers.
150 customers prefer the Cranberry Walnut Scones. So 317 - 150 = 167 customers prefer the Chocolate Chip Scones.
81 of those are male, so 167 - 81 = 86 are female.
So the total of desired outcomes is 86 + 145 = 231
Total outcomes:
317 total customers.
Probability:
231/317 = 0.729
So the correct answer is:
3. 72.9%
why does (0.02)^2 x (0.01) ) / (0.5)^2= 1.6 x 10-5
Answers
Answer:
\(1.6*10^{-5}\)
Step-by-step explanation:
\(\displaystyle \frac{0.02^2*0.01}{0.5^2}\\\\=\frac{0.0004*0.01}{0.25}\\\\=\frac{0.000004}{0.25}\\\\=\frac{4*10^{-6}}{2.5*10^{-1}}\\\\=\frac{4}{2.5}*10^{-6-(-1)}\\\\=1.6*10^{-5}\)
Hope this helped!
The gradient of a line passes through the points a (-3, -8) and H(x,-4). Find the value of x
Answers
The value of x can be any real number.
To find the value of x when the gradient of a line passes through points A(-3, -8) and H(x, -4), we can use the formula for calculating the gradient (slope) of a line:
Gradient = (change in y) / (change in x)
Given that the gradient is the same between points A and H, we can set up the following equation:
(-8 - (-4)) / (-3 - x) = (change in y) / (change in x)
Simplifying the equation, we have:
(-8 + 4) / (-3 - x) = (-4 - (-8)) / (x - (-3))
-4 / (-3 - x) = 4 / (x + 3)
To eliminate the fractions, we can cross-multiply:
-4(x + 3) = 4(-3 - x)
Simplifying further, we have:
-4x - 12 = -12 - 4x
Rearranging the terms, we get:
-4x + 4x = -12 + 12
0 = 0
The equation simplifies to 0 = 0, which means that the value of x can be any real number. In other words, there are infinitely many possible values of x for which the gradient of the line passing through points A and H remains the same.
for such more question on real number
https://brainly.com/question/16444481
#SPJ8
 A student solved the following equation using the following stepsi
4(2 - 3x) = x - 2(2x + 1)
8 - 3x = x - 4x - 2
8 - 3x = -3x - 2
y = 0
Based on the student's work, the equation was solved
The equation solved correctly would show that it has
solution(s).
Word Bank:
correctly
three
infinite
incorrectly
00
TWO
one
Blank 1:
Blank 2:

Answers
Based on the student's work, the equation was solved incorrectly. B. The equation solved correctly would show that it has one solution(s).
What is an equation?A mathematical definition of an equation is a claim that two expressions are equal when they are joined by the equals sign ("="). For instance, 2x - 5 = 13. Two expressions are combined in an equation using an equal symbol ("="). The "left-hand side" and "right-hand side" of the equation are the two expressions on either side of the equals sign.
In correct solution of the equation is given as:
4(2 - 3x) = x - 2(2x + 1)
8 - 12x = x - 4x - 2
8 - 12x = -3x - 2
8 + 2 = 12x - 3x
10 = 9x
x = 10/9
Hence, based on the student's work, the equation was solved incorrectly.
The equation solved correctly would show that it has one solution(s).
Learn more about equations here:
https://brainly.com/question/29657992
#SPJ1
use the shell method to find the volume generated by revolving the shaded regions bounded by the curves and lines in exerciss 7-12about the y-axis
Answers
The answer is 1) V = \(2\pi\int\limits(2)+ {x} \, dx\); 2) V = \(2\pi \int\limits(1 - 2x) - 2x dx\); 3) V =\(2\pi \int\limits {\sqrt{2} } \, dx\) ; 4) V = \(2\pi\int\limits {\sqrt{(-2/2)(2-2)} \ dx\) .
1) The volume of the shell is then given by the product of the area of its curved surface and its height. The height is equal to 2 - (-2) = 4, and the radius is equal to the minimum of the distances from x = 2 to the two curves, which is x = 2 - () = 2 + . The volume of the solid is then given by the definite integral:
V = \(2\pi\int\limits(2)+ {x} \, dx\) = \(2\pi [(/3) + 2x]\) evaluated from 0 to 1 = (4/3)π.
2) The height of the region is equal to - (2x) = -2x, and the radius is equal to the minimum of the distances from x = 1 to the two curves, which is x = 1 - (2x) = 1 - 2x. The volume of the solid is then given by:
V = \(2\pi \int\limits(1 - 2x) - 2x dx\)=\(2\pi [/5 - 2/3 + /2]\) evaluated from 0 to 1 = (8π/15).
3) The height of the region is equal to (2-x) - = 2-x. The radius is equal to the minimum of the distances from x = 0 to the two curves, which is x = The volume of the solid is then given by:
V =\(2\pi \int\limits {\sqrt{2} } \, dx\) = \(2\pi [(x^4/4)]\) evaluated from 0 to √2 = (π/2).
4) The height of the region is equal to () - (2-) = 2 - 2. The radius is equal to the minimum of the distances from x = 0 to the two curves, which is x = √((2-)/2). The volume of the solid is then given by:
V = \(2\pi\int\limits {\sqrt{(-2/2)(2-2)} \ dx\) = \(4\pi [(2/3)\± (2\sqrt{2} /3)]\)
The complete Question is:
Use the shell method to find the volumes of the solids generated by revolving the regions bounded by the curves and lines in about the
1. y = x, y = -x/2, and x = 2
2. y = 2x, y = x/2, and x = 1
3. y = x/2, y = 2-x, and x = 0
4. y = 2-x/2, y = x/2, and x = 0
To know more about Shell Methods:
brainly.com/question/17074517
#SPJ4
Ordena de mayor a menor el siguiente grupo de fracciones y decimales
-2,14; 7/50; -2,41; -11/8; -2,1
Answers
Answer:
-2.41: -2.14: -2.1: -11/8: 7/50
In the equation y=9x - 5, the y-intercept is -5.
Question 3 options:
True
False
Answers
Answer:
true
Step-by-step explanation:
y=mx+b
and b=y intercept
Answer:
True
Step-by-step explanation:
9 is the x intercept and -5 is the y intercept. y in the equation is the answer.
How come the π/6 is equal to 1/2 and radical 3 over 2?
Answers
Answer:
cos(π/6)= radical 3 over 2 sin(π/6) = 1/2
Step-by-step explanation:
In the unit circle the coordinates of the point for the particular angle can be expressed by cos(x) for the x value and sin(x) for the y value. For π/6, the point's x value is radical 3 over 2 as expressed by cos(π/6) and the y value is 1/2 as expressed by sin(π/6)

Calculate the value for the for the following scores 20, 60, 30, 50 given:
begin inline style begin display style sum for blank of end style end style x squared =
Answers
The sum of the scores is equal to 160.
What is a mean?In Mathematics, a mean is sometimes referred to as an average and it can be defined as a ratio of the sum of the total number in a data set (population) to the frequency of the data set.
How to calculate the mean for a data set?Mathematically, the mean for this set of scores can be calculated by using the following formula:
Mean = [F(x)]/n
For the total number of scores (data set), we have;
∑x = 20 + 60 + 30 + 50
∑x = 160.
Mean = [F(x)]/n = 160/4 = 40.
Read more on mean here: brainly.com/question/9550536
#SPJ1

Answer 1, 2, and 3.
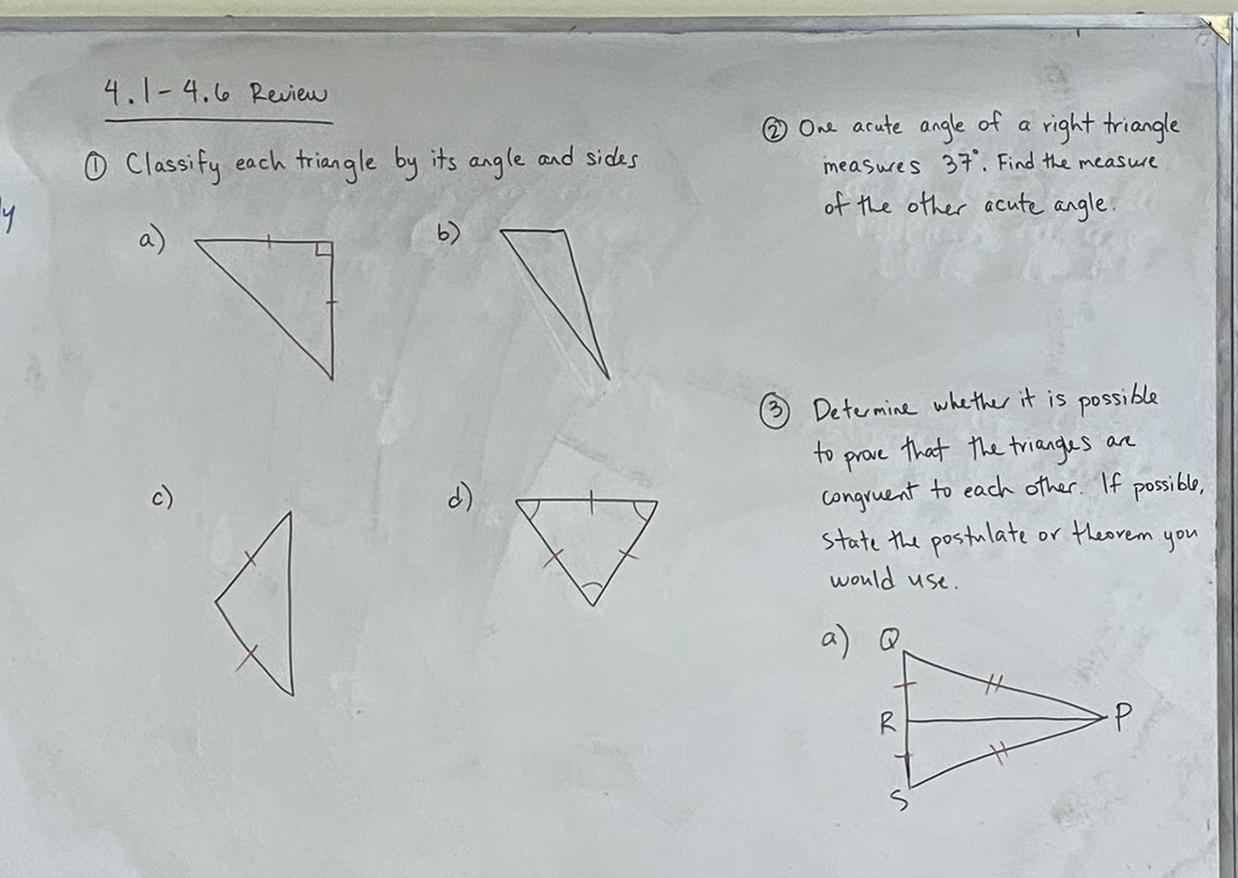
Answers
Answer:
1.
a) isosceles right triangle
b) scalene triangle
c) isosceles triangle
d) equilateral triangle
2. 53 degrees
3. Yes. You can use the side-side-side (SSS) postulate because side QR and side SR are shown as congruent, and side QP and SP are also congruent. Since you know that the other two sides are congruent, then that means that the last side must be congruent as well.
Step-by-step explanation:
how would i anwser this? help pls!

Answers
Answer:
Step-by-step explanation:
To get the y values all you need to do is substitute the x value in the equation y=-2/3x+7.
For example:
y=-2/3(-6)=7
-2/3x6=-4
-4+7=3
(-6,3)
You can double check your work by filling the x and y coordinates in the equation and when solved if it it true you know you were correct.
To get the x value, you need to fill in the y in the equation y=-2/3x+7
for example:
5=-2/3x+7
-2=-2/3x
3=x
(3,5)
y=-2/3x+7
y=-2/3(15)+7
y=-10+7
y=-3
(15,-3)
y=-2/3x+7
15=-2/3x+7
8=-2/3x
-12=x
(-12,15)
Janice got a raise in her hourly pay, from $9.75 to $11.50. Find the percent change. Round to the nearest tenth of a percent.
Answers
Answer:
trhe answer is 11.50 because it's closest to 10
Answer:
17.9%
Step-by-step explanation:
11.50-9.75=1.75
1.75/9.75=0.1794
Find the value of x for which the lines p and q are parallel.

Answers
Answer:
D
Step-by-step explanation:
have a good day
Answer:
D) 7
Step-by-step explanation:
Since the two angles marked are corresponding, if \(p\) and \(q\) are parallel, they must be equal.
Therefore, we have:
\(14x+18=116,\\14x=98,\\x=\boxed{7}\)
what is the range of the function graphed below

Answers
Answer:
-3 < y ≤ 3
Step-by-step explanation:
...............
Compute the following using a calculator.
csc(203∘)
Round your answer to the nearest thousandth, and only include the numerical value in your answer - do not write cscθ= in your response.
Answers
Using a calculator, the value of csc (203°) is -1.086
How to compute csc (203°) using a calculator?Trigonometry is a branch of mathematics dealing with the relationship between the ratios of the sides of a right-angled triangle with its angles.
Since csc (203°) = 1/[sin (203°)]
Press 1/ [sin (203°)] and then the equal to button on your calculator. We have:
1/[sin (203°)] = -1.086
Note: If you calculator have "cosec" or "csc" button, you can simply press cosec (203°) or csc (203°) to get the answer.
Thus, the value of csc (203°) is -1.086
Learn more about Trigonometry on:
brainly.com/question/11967894
#SPJ1
Suppose that a study of elementary school students reports that the mean age at which children begin reading is 5.3 years with a standard deviation of 1.1 years.
Step 1 of 2: If a sampling distribution is created using samples of the ages at which 35 children begin reading, what would be the mean of the sampling distribution of sample means? Round to two decimal places, if necessary.
Answers
Answer:
The mean of the sampling distribution of sample means is equal to the population mean, which is 5.3 years.
give thanks for more! your welcome!
Step-by-step explanation:
The original cost of a sofa was $600. If it was discounted 40% and sales tax is 8%, what is the final cost of the sofa
Answers
Answer:
$312
Step-by-step explanation:
10% of $600 is $60
So $60*4=$240
$600-$240=$360
1%=$6
So $6*8=$48
$360-$48=$312
2. The ramp above connects two vertical supports,
forming two similar triangles: AADE~ AABC. Side AC corresponds to which side in the other triangle?
Answer:
3. What is the length of side BC?

Answers
The side AC corresponds to the side AC in the other triangle and the length of BC is 15 units
Side AC corresponds to which sideFor two triangles to be similar, the corresponding sides of the triangles must be in proportion
Having said that
The side AC corresponds to the side AC in the other triangle
What is the length of side BC?The length BC is calculated as
BC/9 = 25/15
Express as products
So, we have
BC = 9 * 25/15
Evaluate the products
BC = 15
Hence, the length of BC is 15 units
Read more about similar triangles at
https://brainly.com/question/14285697
#SPJ1
how do fund the intervals?
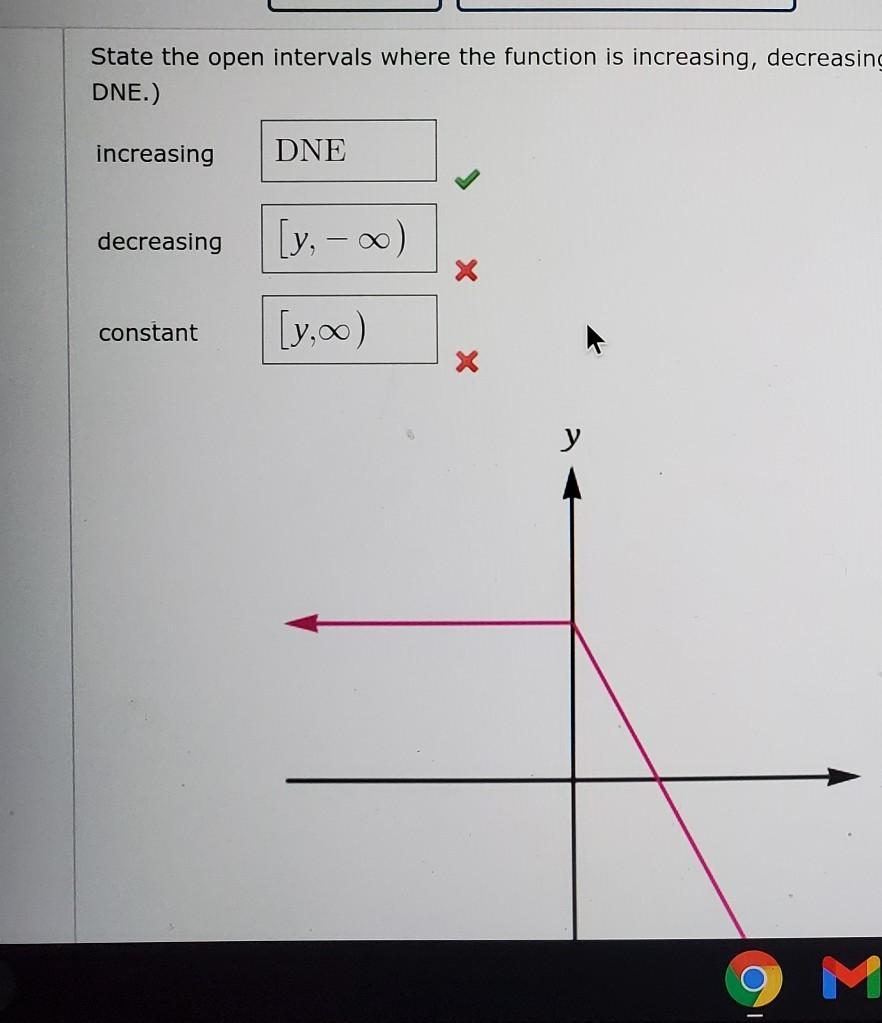
Answers
Answer:
Decreasing: y, infinity
Constant: y, negative infinity
Step-by-step explanation:
You just had it backwards, the interval for infinity is based on the x-axis not the y-axis. The decreasing portion is moving toward positive infinity on the x-axis because it's moving to the right. The constant is moving to the left so it is negative infinity.
PLEASE HELP DUE IN 1 HOUR

Answers
√2500 evaluates to 50 because the number of ice cream cones cannot be negative.
How to evaluate the square root and interpret it in terms of the problem?Given that √2500 represents the number of ice cream cones an ice shop sells in one Saturday
Let's evaluate the square root:
√2500 = ± √2500
= ± 50
= 50 or -50
Thus, the number of ice creams cones = 50
(Note: √2500 is -50 or 50 because (-50)² = 2500 and (50)² = 2500)
The number of ice cream cones is 50 because the number of ice cream cones cannot be negative.
Learn more about evaluation of square root on:
https://brainly.com/question/3617398
#SPJ1
Can you Please help me. With this
