-47 times a number minus 37 is equal to 32 less than the number
Answers
We have a number x.
A number minus 37, times (-47) is equal to 32 less than the number.
The number x minus 37 is (x-37). If we multiply it by (-47) we get -47(x-37).
This is equal to 32 less than x, that is x-32.
Then, we can write:
\(-47(x-37)=x-32\)We can find the number x as:
\(\begin{gathered} -47x-37=x-32 \\ -37+32=x+47x \\ -5=48x \\ x=-\frac{5}{48} \end{gathered}\)Answer: the number is -5/48.
Related Questions
WHAT IS THE RANGE OF 28 42 36 23 14 47 40
Answers
Answer:
33
Step-by-step explanation:
To solve for the range, simply subtract the largest-value term from the smallest-value term. First, set all numbers from least to greatest:
14 , 23 , 28 , 36 , 40 , 42 , 47
The smallest term is 14.
The largest term is 47.
Subtract 47 with 14:
\(47 - 14 = 33\)
The given range value will be 33.
Learn more about solving for range of a given number set, here:
https://brainly.com/question/20607770
Sorry if I’m wrong
Write the equation of the line in a slope-intercept form

Answers
Answer:
It is roughly a 13/32 slope.
Step-by-step explanation:
Rise 40, Run 2
Answer: 40/2
Step-by-step explanation:
What is the answer to : (d+2)(-7)=
Answers
Answer:
-7d - 14
Step-by-step explanation:
that is the answer
\(\huge\text{Hey there!}\)
\(\large\textsf{(d + 2)(-7)}\\\\\large\text{DISTRIBUTE}\\\large\textsf{(d)(-7) + (2)(-7)}\\\large\textsf{(-7)(d) = -7d}\\\laefe\textsf{2(-7) = -14}\\\large\textsf{= \bf -7d - 14}\\\\\boxed{\boxed{\large\textsf{Answer: \huge \bf -7d - 14}}}\huge\checkmark\)
\(\text{Good luck on your assignment and enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
Out of 200 students in a senior class, 32 seniors are in the band and 64 seniors are in the band or on the honor roll. What is the probability that a randomly selected senior is both in the band and on the honor roll? Express your answer a fraction in simplest form.
Answers
The Probability that a randomly selected senior is both in the band and on the honor roll is 8/25.
To find the probability that a randomly selected senior is both in the band and on the honor roll, we need to divide the number of seniors who are in both categories by the total number of seniors.
Given:
Total number of seniors = 200
Number of seniors in the band = 32
Number of seniors in the band or on the honor roll = 64
Let's calculate the probability using these values:
Probability = Number of seniors in both categories / Total number of seniors
Probability = 64 / 200
To simplify this fraction, we can divide both the numerator and denominator by their greatest common divisor, which is 8:
Probability = (64 ÷ 8) / (200 ÷ 8)
Probability = 8 / 25
Therefore, the probability that a randomly selected senior is both in the band and on the honor roll is 8/25.
For more questions on Probability .
https://brainly.com/question/24756209
#SPJ8
Find the area of the shape shown below
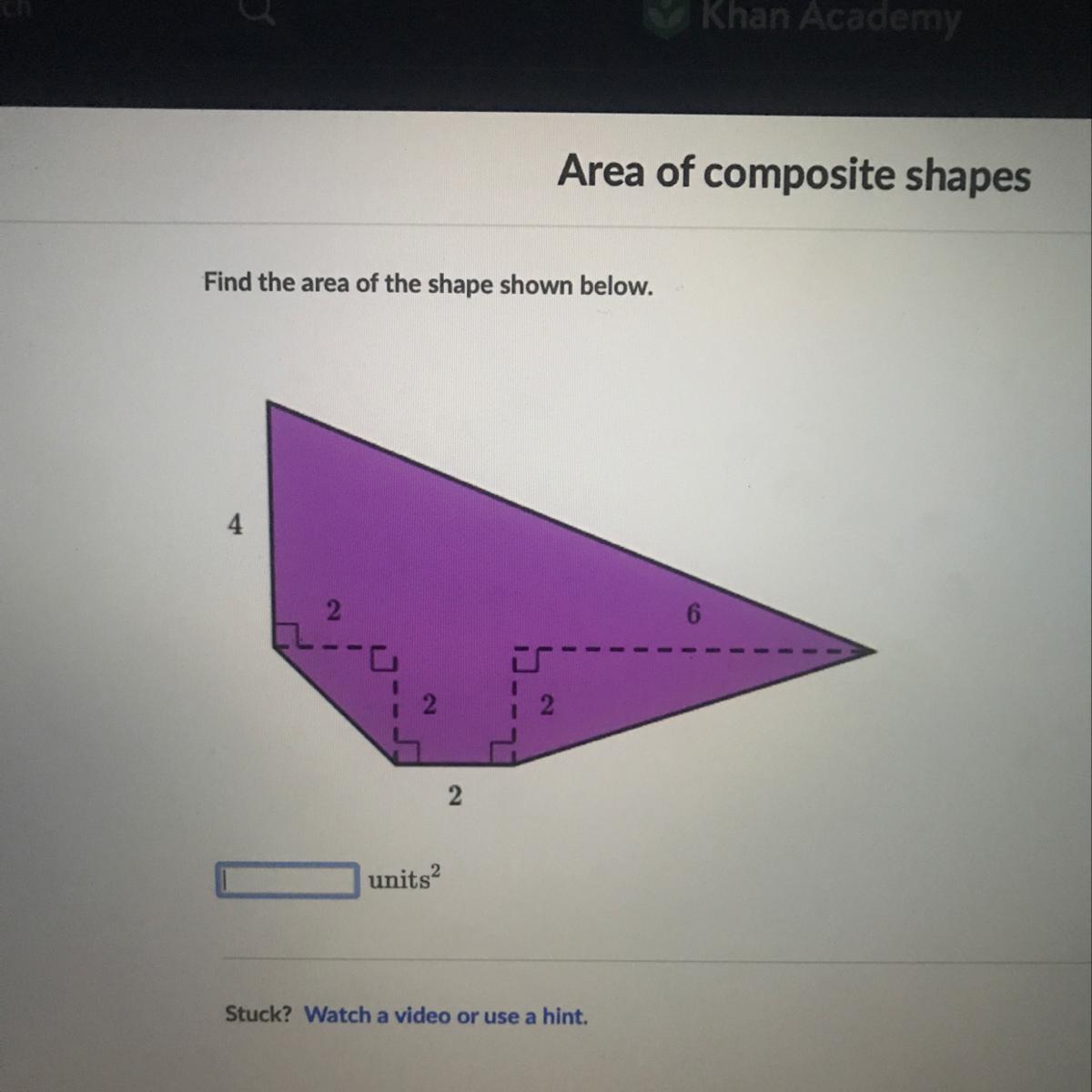
Answers
Answer: whats the area
The function f(x) = 1.85x2 models the cost of a square carpet, where x is the length in feet. Find the average rate of change for f, to the nearest tenth, over the interval 10 ≤ x ≤ 20.
Answers
To find the average rate of change of the function f(x) = 1.85x^2 over the interval 10 ≤ x ≤ 20, we need to find the difference in the function values at the endpoints of the interval and divide by the length of the interval.
The function value at x = 10 is:
f(10) = 1.85(10)^2 = 185
The function value at x = 20 is:
f(20) = 1.85(20)^2 = 740
The length of the interval is:
20 - 10 = 10
So the average rate of change of the function over the interval 10 ≤ x ≤ 20 is:
(f(20) - f(10)) / (20 - 10) = (740 - 185) / 10 = 55.5
Rounding to the nearest tenth, the average rate of change of the function over the interval 10 ≤ x ≤ 20 is approximately 55.5.
find the difference below as a fraction 6/2_7/7
Answers
Answer:
2
Step-by-step explanation:
\(\frac{6}{2}\) - \(\frac{7}{7}\) First simplify each fraction
\(3\) - 1 Then solve
2 Final answer
Find the volume of the cylinder to the nearest cubic foot. Use a calculator. A. 236 ft3 B. 942 ft3 C. 251 ft3 D. 75 ft3

Answers
\(\textit{volume of a cylinder}\\\\ V=\pi r^2 h~~ \begin{cases} r=radius\\ h=height\\[-0.5em] \hrulefill\\ r=5\\ h=3 \end{cases}\implies V=\pi (5)^2(3)\implies V\approx 236~ft^3\)
Answer:
236 ft^3
Step-by-step explanation:
Base radius = 5 ft
Height = 3 ft
Volume = πr^2h
= π × 5^2 × 3
= 75π
= 235.61944901923 feet^3
Nearest Cubic Foot = 236 ft^3
Nearest Cubic Foot:
Hence Answer is:
236 ft^3
Hope this helps!
Andrew drinks 1.9 litres of water each day for three years. By rounding the amount of water an the number of days to one significant figure find the approximate amount of water he drinks during the three years. [One year = 365 or 366 days]
Answers
Answer:
2081days or 2086days
Step-by-step explanation:
1.9(365)=693.5
1.9(366)=695.4
693.5(3)=2080.5
695.4(3)=2086.2
A house is on an 80,000 sq. ft lot. About how many acres is the lot? There are 43.560 square feet in a acre?
Answers
Mbali walks to the lake every third day. Nqabisa walks to the lake every
fourth day. Calculate how often they will walk to the lake on the same day
Answers
Step-by-step explanation:
we need to find the LCM, the least (or lowest) common multiple, of 3 and 4.
that means the smallest number that can be divided by 3 and by 4 without remainder.
and that is simply in our case 3×4 = 12.
so, every 12th day they will walk to the lake "together" (on the same day).
FYI - formality the LCM is found e.g. by prime factorization.
starting with the smallest prime number (2) both numbers are divided by the prime number, if there is no remainder. the quotient is then again divided by the prime number. if there is a remainder, then the next higher prime number is taken for the division.
this goes on until we get a quotient of 1.
the LCM is then the product of the longest streaks of the products of the same prime numbers.
example LCM of 56 and 50
56 ÷ 2 = 28 (0 remainder)
28 ÷ 2 = 14 (0 remainder)
14 ÷ 2 = 7 (0 remainder)
7 ÷ 2 has a remainder, so the next prime number (3)
7 ÷ 3 has a remainder, so the next prime number (5)
7 ÷ 5 has a remainder, so the next prime number (7)
7 ÷ 7 = 1 finished
50 ÷ 2 = 25 (0 remainder)
25 ÷ 2 has a remainder, so the next prime number (3)
25 ÷ 3 has a remainder, so the next prime number (5)
25 ÷ 5 = 5 (0 remainder)
5 ÷ 5 = 1 finished
the longest streaks of prime number products :
2×2×2 = 8
5×5 = 25
7 = 7
the LCM = 8×25×7 = 1400
please consider, this is NOT 56×50 = 2800.
the LCM is not automatically just the product of both numbers. this product is a common multiple, true, but not always the smallest.
in our case here with 3 and 4
3 ÷ 2 has a remainder, so the next prime number (3)
3 ÷ 3 = 1 finished
4 ÷ 2 = 2 (0 remainder)
2 ÷ 2 = 1 finished
the longest prime number product streaks :
2×2 = 4
3 = 3
the LCM = 4×3 = 12
so, in this case the LCM is the direct product of both numbers.
A new city park will have a path from the southeast corner to the northwest corner. The shape of the park is rectangular. With the information given, determine how many yards long the path will be. The rectangles length is 50 yd and the width is 120 yd

Answers
The length of the path is 130 yards
How to determine the value
To determine the value of the path, c, we need to know the Pythagorean theorem
Using the Pythagorean theorem which states that the square of the longest leg of a triangle is equal to the sum of the squares of the other two sides of the triangle.
In this case, we have that;
c² = length² + width²
Substitute the values from the information given, we have that;
c² = 50²+ 120²
Find the squares, we get;
c² = 2500 + 14, 400
add the values, we get;
c² = 16900
c = 130 yards
Learn more about Pythagorean theorem at: https://brainly.com/question/654982
#SPJ1
A borrower has a monthly payment of $1,980 on a loan with a monthly constant of 6.45. What is the loan amount (to the nearest hundred)
Answers
Answer:
loan amount = $307,000
Step-by-step explanation:
given data
monthly payment = $1,980
monthly loan constant = 6.45
to find out
loan amount
solution
we get here loan amount that is express as
loan amount = ( monthly payment ÷ monthly loan constant ) × 1000 .........1
put here value
loan amount = ( 1980 ÷ 6.45 ) × 1000
loan amount = $307,000
Is it possible to construct a triangle with side lengths of 6, 7, and 11 units? If not, explain why not.
no; 6+7 11
no; 11 +746
no; 6 + 1147
yes
Answers
Answer:
No, we cannot construct the triangle with a side length of 6, 7, and 11 units. It is because the sum of the two sides of the triangle must be greater than the hypotenuse of the triangle.
Answer:
yes
Step-by-step explanation:
sum of any two sides> third side
difference of any two sides<third side
6+7=13>11
11+6=17>7
11+7=18>6
11-6=5<7
11-7=4<6
which is true .
Solve x2 – 8x + 15 < 0. Select the critical points for the inequality shown. –15 –5 –3 3 5
Answers
The critical points are within rthe range 3<x<5
Quadratic equationsThese are equations that has a leading degree of 2. Given the expression below.
x²-8x+15<0
Factorize
x²-3x-5x+15<0
Factor out the GCF
x(x-3)-5(x-3) <0
Group
(x-3)(x-5)<0
Find the solution
x < 3 and x <5
Hence the critical points are within rhe range 3<x<5
Learn more on inequality here;https://brainly.com/question/24372553
#SPJ1
The length of a rectangle is 5 cm less than 3 times its width. If the perimeter is 54 cm, find its length.
Answers
Answer:
W = 8cm
L = 19cm
Step-by-step explanation:
The first step to solving these problems is always writing the information that is given into 2 equations.
Piece of info #1: Length is 5cm less than 3 times the width
Piece of info #2: Perimeter (of the rectangle, which has 4 sides) is 54cm
Turing these into equations...
Equation 1) L = 3*W - 5
Equation 2a) L+L+W+W = 54
Let's simplify that second equation:
Equation 2b) 2L+2W = 54
Now, we just solve the system of two equations by substitution. Take the known value of L from equation 1 and substitute it in for the value of L in equation 2b:
2*(3*W-5)+2W = 54
Now we solve for W:
6W - 10 + 2W = 54
8W - 10 = 54
8W = 64
W = 64/8
W = 8 cm
Now that we know W, we can substitute its value into either equation 1 or equation 2 to find L. Here, I'll randomly choose equation 1.
Equation 1) L = 3*W - 5
L = 3*8 - 5
L = 24-5
L = 19 cm
a triangular prism (like a box of toblerone) of mass m, whose two ends are equilateral triangles parallel to the xy plane with side 2a, is centered on the origin with its axis along the z axis. find its moment of inertia for rotation about the z axis. without doing any integrals write down and explain its two products of inertia for rotation about the z axis.
Answers
The moment of inertia for rotation about the z axis is \(I & =\frac{a^2 M}{3}\).
A triangular prism of mass m, whose two ends are equilateral triangles.
Two ends are equal.
The xy plane with side 2a, is centered on the origin with its axis along the z axis.
Find the moment of inertia for rotation the z-axis.
It is divide into 4 triangles with side 'a' k one side is 3cm.
\($$\begin{aligned}& I_{\text {BiG }}=16 I_{\text {small }} . \\& I_{\text {BIG }}=4 I_{\text {small }}+P_{A T}\end{aligned}$$\)
It is fact that the big triangle is made up from four small triangles. connected with parallel axis theorem.
Now, we have to find the distance from the center of mas of small outer triangles to the origin. so, that it is PAT.
\($$\therefore z=2 \sqrt{x^2-\frac{a}{2} ^2}$$\)
\($$\begin{aligned}& =2 \sqrt{\left(\frac{a}{\sqrt{3}}\right)^2-\frac{a^2}{4}} \\& =2 \sqrt{\frac{a^2}{3}-\frac{a^2}{4}} \\I_{\text {Big }} & =\frac{\sqrt{3}}{3} a \cdot \\& \left.=4 I_{\text {small }}+3 m \frac{\sqrt{3}}{3} a\right)^2 \\I_{\text {Big }} & =4 I_{\text {small }}+\frac{3 m}{4} \frac{1}{3} a^2 \\& =\frac{a^2}{4}\end{aligned}$$\)
⇒ Now, by using the \($I_{\text {Big }}=I$\)
⇒\(I & =4\left(\frac{\sqrt{2}}{16}\right)+\frac{a^2 M}{4} \\\)
⇒\(4 I & =I+a^2 m\)
⇒\(4 I-I & =a^2 m \\\)
⇒\(3 I & =a^2 M . \\\)
⇒\(I \quad & =\frac{a^2 M}{3}\)
Therefore, the moment of inertia is \(I & =\frac{a^2 M}{3}\).
For more such questions on distance between points
https://brainly.com/question/15958176
#SPJ4
Find the quotient of 3/5 3/7. Write your answer in the simplest form.
Answers
\(\cfrac{3}{5}\div\cfrac{3}{7}\implies \cfrac{~~\begin{matrix} 3 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}{5}\cdot \cfrac{7}{~~\begin{matrix} 3 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}\implies \cfrac{7}{5}\implies 1\frac{2}{5}\)
3- 2 1/3×3/14+1 1/3÷4/5
Answers
Answer:
4.166 or 4.17 or 4 7/100
Step-by-step explanation:
Please consider giving me brainliest.
Have a good day<3 Bye!
Answer: 4.17
It is the right answer, I just checked it.
Find the inversion point of the given point (4, 5) with respect to the circle x² + y² - 4x - 6y - 3 = 0. Also, show in the graph.
Answers
The inversion point of (4, 5) with respect to the circle x² + y² - 4x - 6y - 3 = 0 is (6, 7).
Finding the inversion pointTo find the inversion point of the given point (4, 5) with respect to the circle x² + y² - 4x - 6y - 3 = 0, we need to follow these steps:
Step 1: Write the equation of the given circle in standard form by completing the square for x and y: (x - 2)² + (y - 3)² = 16.
Step 2: Find the radius of the circle by taking the square root of the constant term: r = √16 = 4.
Step 3: Find the distance between the given point (4, 5) and the center of the circle (2, 3) using the distance formula: d = √[(4 - 2)² + (5 - 3)²] = √8.
Step 4: Use the formula for inversion point to find the coordinates of the inversion point (x', y'): (x', y') = (h + r²/d² * (x - h), k + r²/d² * (y - k)), where (h, k) is the center of the circle and r is the radius.
Plugging in the values, we get: (x', y') = (2 + 4²/8 * (4 - 2), 3 + 4²/8 * (5 - 3)) = (6, 7).
Therefore, the inversion point of the given point (4, 5) with respect to the circle x² + y² - 4x - 6y - 3 = 0 is (6, 7).
Read more about conic section at
https://brainly.com/question/29192791
#SPJ1
who ever gets this right will get brainleist
Which table has a constant of proportionality between yyy and xxx of 1.51.51, point, 5?
Choose 1 answer:
Choose 1 answer:
(Choice A)
Answers
Answer:
Need more info
Step-by-step explanation
TOPIC=Rearranging
Task:Make x the subject of these equations
6x + v = 4x + w
ax + 9 = 2x + b
7x - w = vx+4
6 - wx = vx + 4
3(wx-v) = 4(x+v)
Answers
All the solutions are,
⇒ x = 1/2 (w- v)
⇒ x = (b - 9)/(a - 2)
⇒ x = (4 + w) / (7 - v)
⇒ x = 2 / (v + w)
⇒ x = 7v/(3w - 4)
Given that;
Expressions are,
⇒ 6x + v = 4x + w
⇒ ax + 9 = 2x + b
⇒ 7x - w = vx+4
⇒ 6 - wx = vx + 4
⇒ 3(wx - v) = 4(x + v)
We can simplify as;
⇒ 6x + v = 4x + w
⇒ 6x - 4x = w - v
⇒ 2x = w - v
⇒ x = 1/2 (w- v)
⇒ ax + 9 = 2x + b
⇒ ax - 2x = b - 9
⇒ (a - 2)x = b - 9
⇒ x = (b - 9)/(a - 2)
⇒ 7x - w = vx+4
⇒ 7x - vx = 4 + w
⇒ (7 - v) x = 4 + w
⇒ x = (4 + w) / (7 - v)
⇒ 6 - wx = vx + 4
⇒ vx + wx = 6 - 4
⇒ (v + w)x = 2
⇒ x = 2 / (v + w)
⇒ 3(wx - v) = 4(x + v)
⇒ 3wx - 3v = 4x + 4v
⇒ 3wx - 4x = 7v
⇒ (3w - 4)x = 7v
⇒ x = 7v/(3w - 4)
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
1.1.3. How many litres of milk does Lihle need to make 120 cupcakes? (2)
Answers
Lihle would need 30 liters of milk to make 120 cupcakes.
To determine the amount of milk Lihle needs to make 120 cupcakes, we can calculate the total milk requirement by multiplying the milk quantity per cupcake by the number of cupcakes.
Given that the recipe requires 250 milliliters (ml) of milk per cupcake, we can proceed with the calculation:
Convert milliliters to liters:
Since there are 1,000 milliliters in a liter, we divide 250 ml by 1,000 to get the milk quantity per cupcake in liters, which is 0.25 liters.
Multiply the milk quantity per cupcake by the total number of cupcakes: Multiply 0.25 liters (milk per cupcake) by 120 cupcakes.
0.25 liters/cupcake \(\times\) 120 cupcakes = 30 liters.
Therefore, Lihle would need 30 liters of milk to make 120 cupcakes in a US curriculum class.
It's important to note that this calculation assumes the given milk requirement of 250 milliliters per cupcake and does not consider any other ingredients or variations in the recipe.
For similar question on amount.
https://brainly.com/question/28147009
#SPJ8
The complete question may be like: Assuming that the recipe requires 250 milliliters (ml) of milk per cupcake, how many liters of milk does Lihle need to make 120 cupcakes in a US curriculum class?
The figure below shows the graph of f’ the derivative of the function f, on the closed interval from x = -2 to x = 6. The graph of the derivative has horizontal tangent lines at x = 2 and x = 4.
find the x-value where f attains it’s absolute maximum value on the closed interval x=-2 to x=6. justify your answer

Answers
Answer:
x = -2
Step-by-step explanation:
The function is decreasing where the first derivative is negative.
That is, the function is decreasing on the interval (-2, 5), except at x=2, where there is a flat spot. That means the maximum value is found at the left end of that interval, at x=-2.
__
The maximum value might be found at x = 6, at the right end of the interval (5, 6) on which the function is increasing. However, we judge the area under the first derivative curve between x=5 and x=6 to be less than the total area under the curve between x=-2 and x=5. That means the function does not increase enough from its minimum at x=5 to make up for the decrease over the longer interval.
__
The attachment shows an approximation of the derivative function given in the problem statement (dashed line) and its integral (solid line). Not all of the curvature of f'(x) is accounted for in the approximation, but the overall result is consistent with the above analysis.

What is the equation of a circle with center (−8, 3) and radius 8?
(x + 8)2 + (y − 3)2 = 64
(x − 8)2 + (y + 3)2 = 64
(x − 8)2 + (y + 3)2 = 8
(x + 8)2 + (y − 3)2 = 8
Answers
Answer:
(x + 8)² + (y - 3)² = 64
Step-by-step explanation:
(x - (-8))² + (y - 3)² = 8²
(x + 8)² + (y - 3)² = 64
Question 1 0.1 pts The initial cost of a pickup truck is $12,659 and will have a salvage value of $3,580 after five years. Maintenance is estimated to be a uniform gradient amount of $135 per year, with zero dollar for first year maintenance. The operation cost is estimated to be $0.2 per mile for 344 miles per month. If the interest rate is 12%, what is the annual equivalent cost (AEC) for the truck? Enter your answer as follow: 123456
Answers
The annual equivalent cost (AEC) for the pickup truck is $4,308. We found the equivalent uniform annual cost (EUAC) first.
To calculate the AEC, we need to first find the equivalent uniform annual cost (EUAC) which includes both the initial cost and the present value of the maintenance and operation costs.
Find the present value of maintenance costs over five years using the gradient formula:
PV maintenance = A * [(1+i)^n - (1+i- g)^n] / [i - g]where A = $135, i = 12%, g = 0, n = 5
PV maintenance = $501.21
Find the present value of operating costs over five years using the present value formula:
PV operation = C * [1 - (1 + i)^-n] / iwhere C = $0.2/mile * 344 miles/month * 12 months/year = $827.52/year, i = 12%, n = 5
PV operation = $3,322.08
Find the EUAC using the formula:
EUAC = (initial cost + PV maintenance + PV operation) * A/Pwhere A/P = [(1+i)^n * i] / [(1+i)^n - 1]
EUAC = ($12,659 + $501.21 + $3,322.08) * 0.1464EUAC = $2,219.77Finally, convert the EUAC to AEC by adding the present value of the salvage value and multiplying by the interest rate:
AEC = (EUAC + PV salvage) * iwhere PV salvage = $3,580 / \((1+i)^5\)
AEC = ($2,219.77 + $2,267.03) * 0.12AEC = $4,308.Learn more about Cost and Estimate:
https://brainly.com/question/28621647
#SPJ4
Jackie runs and dances for 75 minutes every day.
She dances 25 minutes more than she runs.
What is the greatest amount of time she could spend dancing every day,
given she will take a run.
Answers
Answer:
I think it is 50 because 75-25=50
Please help me this is hard

Answers
Shaded Area=11*14 -5*7= 154- 35=119 sqm
In the diagram below of circle O, chords AD and BC intersect at E, and chords AB and CD are drawn.
Which statement must always be true?
PLEASE HELP!

Answers
The correct answer is (C) \(\angle B \cong \angle C.\) when In the diagram below of circle O, chords AD and BC intersect at E.
What is a circle ?
A circle is a two-dimensional geometric shape that consists of all the points in a plane that are at a fixed distance from a given point, called the center.
In the given diagram, we have a circle O with chords AB, CD, AD, and BC. The chords AD and BC intersect at point E.
Based on the diagram, we can see that the opposite angles in the quadrilateral AEDC are supplementary (i.e., they add up to 180 degrees). Therefore, we have:
\(\angle A + \angle C = 180^\circ\)
Similarly, the opposite angles in the quadrilateral BEFC are supplementary. Thus,
\(\angle B + \angle C = 180^\circ\)
We can rewrite the second equation as:
\(\angle C = 180^\circ - \angle B\)
Substituting this value of \angle C into the first equation, we get:
\(\angle A + 180^\circ - \angle B = 180^\circ\)
Simplifying, we get:
\(\angle A = \angle B\)
Therefore, the correct answer is (C) \(\angle B \cong \angle C.\)
To learn more about chords visit the link :
https://brainly.com/question/1654080
#SPJ1
Please help me answer this

Answers
Answer:
The answer is B
Step-by-step explanation:
Btw if its wrong im sorry