4x-2(3x+7)=____x-_____
Answers
Answer: x = -9
Step-by-step explanation: 4
x
+
2
=
3
x
−
7
⇒
4x−3x=−7−2⇒x=−9
Related Questions
Four friends paid a total of $32 for bowling. What is the ratio $32 for 4 people written as a unit rate?
Answers
Answer:
$8 per person
Step-by-step explanation:
32 divided by 4 is 8
32 : 4 = 8 : 1
A tank is full of water. Find the work required to pump the water out of the spout. (Use 9.8 m/s2 for g. Use 1000 kg/m3 as the density of water. Assume r = 6 m and h = 2 m.)
Answers
The work required to pump the water out of the spout is 70.9 * 10⁶ joules which is 71 M Joules approx.
Let the spherical tank be divided into a series of horizontal disks.
Let x be the height of each disk, g = gravity and p = density
Volume of each disk = πr2dx
Where r is the radius of each disk and dx is the thickness
By Pythagoras r² = 6² - x²= 36 -x²
Therefore Volume = π*(36-x²)*dx cubic metres
The distance each disk has to be lifted to escape the top of the spout = 2 + 6-x meters = (8-x)
Work needed to lift each disk to outlet = distance * mass where
mass = volume * density * gravity
= pi(36-x²)*p*g = 9800pi(36-x²)dx
dW = (8-x)* 9800pi(36-x²)dx
Since we have already accounted for the height of the spout, the work required is obtained by integrating the above expression from the bottom of the tank to the top. In other words, - 6 to + 6.
W = ⌠(8-x)*9800pi(36-x2)dx = 9800pi⌠[288 - 36x - 8x² +x³]dx
The odd terms evaluate to zero and we can rewrite the above as 2* I from 0 to 6.
W = 9800pi*2 [288x - 8x³/3] at x = 6 = 1152*19600π Joules = 22579200π joules = 70963200j
Total work required = 70.9 * 10⁶ joules
Visit here to learn more about spherical tank: https://brainly.com/question/11279278
#SPJ4
Calculus problem: A drug manufacturer has developed a time-release capsule with the number of milligrams of the drug in the bloodstream given by
S = 40\(x^{\frac{19}{7} }\) − 560\(x^{\frac{12}{7} }\) + 1960\(x^{\frac{5}{7} }\)
where x is in hours and 0 ≤ x ≤ 7. Find the average number of milligrams of the drug in the bloodstream for the first 7 hours after a capsule is taken. (Round your answer to the nearest whole number.)
Solution: _____ mg
Answers
Step-by-step explanation:
You can find your answer by taking integral from 0 to 7 and then dividing it by 7.

Screenshot below will hold the question.

Answers
The equation the completes the proof in step 6 is m<w + m<x = m<x + m<z
How to complete the proof?In step 4 of the proof, we have the following equation
m<w + m<x = m<y + m<z
In step 5, we have
m<x = m<y
When m<x = m<y is substituted to the equation in step 4, we have:
m<w + m<x = m<x + m<z
Hence, the equation the completes the proof in step 6 is m<w + m<x = m<x + m<z
Read more about mathematical proofs at:
https://brainly.com/question/1788884
#SPJ1
What is the area of the shaded sector of Point B below?

Answers
Answer:
A) 175π / 9 squared inches,
Step-by-step explanation:
Radius = 10 inches
AB = BD = 10 = radius
Triangle ABD is isosceles
Angle DAB = Angle BDA = 35 degrees,
Base angles theroem
35 + 35 + x = 180, angles in triangle
x = 180 - 70
x = 110 degrees
Angle DBC is supplementary with ABD
110 + x = 180
x = 70
70 degrees is angle for the sector
70 is 70/360, 7/36 of the circle
The area will also be 7/36 of the circle area
Area of circle = πr^2
Area = 100π
Area of sector = (100π * 7) / 36
Area of sector = 700π / 36
Simplified area = 175π / 9 squared inches
A car travels 120 miles from A to B at 30 miles per hour but returns the same distance at 40 miles per hour. The average speed for the round trip is closest to?
Answers
The average speed formula is given by:
\(\displaystyle\sf \text{Average Speed} = \frac{\text{Total Distance}}{\text{Total Time}}\)
Let's calculate the total distance first. The car travels 120 miles from point A to point B, and then returns the same distance. Therefore, the total distance is \(\displaystyle\sf 2 \times 120 = 240\) miles.
Now, let's calculate the total time. The time taken to travel from A to B can be calculated using the formula \(\displaystyle\sf \text{Time} = \frac{\text{Distance}}{\text{Speed}}\).
For the journey from A to B:
\(\displaystyle\sf \text{Time}_1 = \frac{120}{30} = 4\) hours
For the return journey from B to A:
\(\displaystyle\sf \text{Time}_2 = \frac{120}{40} = 3\) hours
The total time for the round trip is the sum of the individual times:
\(\displaystyle\sf \text{Total Time} = \text{Time}_1 + \text{Time}_2 = 4 + 3 = 7\) hours
Now, we can calculate the average speed:
\(\displaystyle\sf \text{Average Speed} = \frac{\text{Total Distance}}{\text{Total Time}} = \frac{240}{7} \approx 34.29\) miles per hour.
Therefore, the average speed for the round trip is closest to 34.29 miles per hour.
HELP!!!
Which point is located at (-5,5)?
point K
point L
point F
point G

Answers
Answer:
The correct answer is point F!
Step-by-step explanation:
Hope it helped :D
Answer:
point f
Step-by-step explanation:
-5 in x and 5 and y
ANSWER: POINT F
3/4 x 12 pls I need help
Answers
Answer:
The correct answer is 9
Step-by-step explanation:
I can assure you this is absolutely correct.
Alex's recipe calls for 1/3 cup of chocolate chips for every 2 cups of flour. If he increases the
amount of flour to 3 cups, how many cups of chocolate chips will he need?
Answers
Answer:
1/2 cup of chocolate chips
Step-by-step explanation:
Given ratio:
chocolate chips : flour = 1/3 cups : 2 cupsLet x be the unknown amount of chocolate chips:
\(\implies \sf \dfrac{1}{3}:2=x:3\)
\(\implies \sf \dfrac{\frac{1}{3}}{2}=\dfrac{x}{3}\)
Cross multiply:
\(\implies \sf 3 \cdot \dfrac{1}{3}=2 \cdot x\)
\(\implies \sf 1=2x\)
\(\implies \sf x=\dfrac{1}{2}\)
Therefore, 1/2 a cup of chocolate chips will be needed for 3 cups of flour.
Let that be x
1/3/2=x/31/6=x/3x=3/6x=1/2 cupI need help !! 3 questions for Algebra please



Answers
Answer:
the questions of Albania we don't know language of albera please don't disturbance and give me 10 marks
Using triangle RST, which side is the hypotenuse

Answers
Answer:
Side RT
Step-by-step explanation:
The hypotenuse is the longest side on a right angle triangle, making it the side RT.
ZABD and ZDBC are supplementary angles,
What is the measure of x?
X = [?]°
7D
110%
AK
B
>C
Angles are not drawn to scale.
Finter
![ZABD and ZDBC are supplementary angles,What is the measure of x?X = [?]7D110%AKB>CAngles are not drawn](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/v04bHz91oMV1D0wbmOfxW80tj8qzKrGV.png)
Answers
Answer:
x=70°
Step-by-step explanation:
x+110=180 linear pair
x=180-110=70
"Consider the following circle with radius 1. The lines A and B are radii, and have a length of 1. Find the area of the shaded region."
I got an area of 1.06 (Rounded), I'm just wondering if that is correct. Any help would be appreciated!

Answers
Answer:
\(\textsf{Area}=\dfrac{5\pi -3}{12} \approx 1.06\; \sf square\;units \;(3\;s.f.)\end{aligned}\)
Step-by-step explanation:
To find the area of the shaded region, subtract the area of the isosceles triangle from the area of the sector.
An isosceles triangle is made up of two congruent right triangles.
To find the height of the right triangles (and thus the height of the isosceles triangle), use the cosine trigonometric ratio.
\(\boxed{\begin{minipage}{9 cm}\underline{Cosine trigonometric ratio} \\\\$\sf \cos(\theta)=\dfrac{A}{H}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
Given values:
The angle is half the apex angle: θ = 5π/12.The side adjacent the angle is the height of the triangle: x.The hypotenuse is the radius: H = 1.Substitute these values into the cosine ratio to calculate the height of the right triangles (and thus the height of the isosceles triangle):
\(\cos \left(\dfrac{5\pi}{12}\right)=\dfrac{x}{1}\)
\(x=\cos \left(\dfrac{5\pi}{12}\right)\)
\(x=\dfrac{\sqrt{6}-\sqrt{2}}{4}\)
The base of one of the right triangles can be found by using the sine trigonometric ratio.
\(\boxed{\begin{minipage}{9 cm}\underline{Sine trigonometric ratio} \\\\$\sf \sin(\theta)=\dfrac{O}{H}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
Given values:
The angle is half the apex angle: θ = 5π/12.The side opposite the angle is the base of the right triangle: y.The hypotenuse is the radius: H = 1.Substitute these values into the sine ratio to determine the base of the right triangle:
\(\sin \left(\dfrac{5\pi}{12}\right)=\dfrac{y}{1}\)
\(y=\sin \left(\dfrac{5\pi}{12}\right)\)
\(y=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
The base of the isosceles triangle is twice the base of the right triangle, so the base of the isosceles triangle = 2y.
Therefore the area of the isosceles triangle is:
\(\begin{aligned}\textsf{Area of isosceles triangle}&=\dfrac{1}{2} \cdot \sf base \cdot height\\\\&=\dfrac{1}{2}\cdot 2y \cdot x\\\\&=\dfrac{1}{2} \cdot 2\left(\dfrac{\sqrt{6}+\sqrt{2}}{4}\right) \cdot \left(\dfrac{\sqrt{6}-\sqrt{2}}{4}\right)\\\\&=\left(\dfrac{\sqrt{6}+\sqrt{2}}{4}\right) \cdot \left(\dfrac{\sqrt{6}-\sqrt{2}}{4}\right)\\\\&=\dfrac{4}{16}\\\\&=\dfrac{1}{4}\sf \;square\;units\end{aligned}\)
To find the area of the sector of the circle, use the area of a sector formula (where the angle is measured in radians).
\(\boxed{\begin{minipage}{6.4 cm}\underline{Area of a sector}\\\\$A=\dfrac12 r^2 \theta$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in radians.\\\end{minipage}}\)
Given values:
r = 1θ = 5π/6Substitute the values into the formula:
\(\begin{aligned}\textsf{Area of the sector}&=\dfrac{1}{2} \cdot (1)^2 \cdot \dfrac{5\pi}{6}\\\\&=\dfrac{1}{2} \cdot 1 \cdot \dfrac{5\pi}{6}\\\\&=\dfrac{1}{2} \cdot \dfrac{5\pi}{6}\\\\&=\dfrac{5\pi}{12}\;\; \sf square\;units\end{aligned}\)
Finally, to find the area of the shaded region, subtract the area of the isosceles triangle from the area of the sector:
\(\begin{aligned}\textsf{Area of the shaded region}&=\sf Area_{sector}-Area_{isosceles\;triangle}\\\\&=\dfrac{5\pi}{12}-\dfrac{1}{4}\\\\&=\dfrac{5\pi}{12}-\dfrac{3}{12}\\\\&=\dfrac{5\pi -3}{12}\\\\&=1.05899693...\\\\&=1.06\; \sf square\;units \;(3\;s.f.)\end{aligned}\)
Therefore, the area of the shaded region is (5π - 3)/12 or approximately 1.06 square units (3 significant figures).
Give the function Calculate the following values: A. F(-1) = B. F(0) = C. F(2) = D. Find two different (exact) values of x such that F(x) = -25. Enter your answers separated by a comma, e.g 1, 2. X = E. The domain of F(x) is _________ Note: write the domain in interval notation. If it includes more than one interval write the intervals separated by the union symbol

Answers
From the function we will have:
a. f(-1):
\(f(-1)=5(-1)-8\Rightarrow f(-1)=-13\)b. f(0):
\(f(0)=-5(0)-16\Rightarrow f(0)=-16\)c. f(2):
\(f(2)=-5(2)-16\Rightarrow f(2)=-26\)d. We will find the values as follows:
\(\begin{cases}5x-8=-25\Rightarrow5x=-17\Rightarrow x=-\frac{17}{5} \\ \\ -5x-16=-25\Rightarrow-5x=-9\Rightarrow x=\frac{9}{5}\end{cases}\)e. The domain of the function is all the real numbers:
\((-\infty,\infty)\)1.5 x 3 equals what
Answers
Answer:
4.5
Step-by-step explanation:
Please help what is the slope of the line?
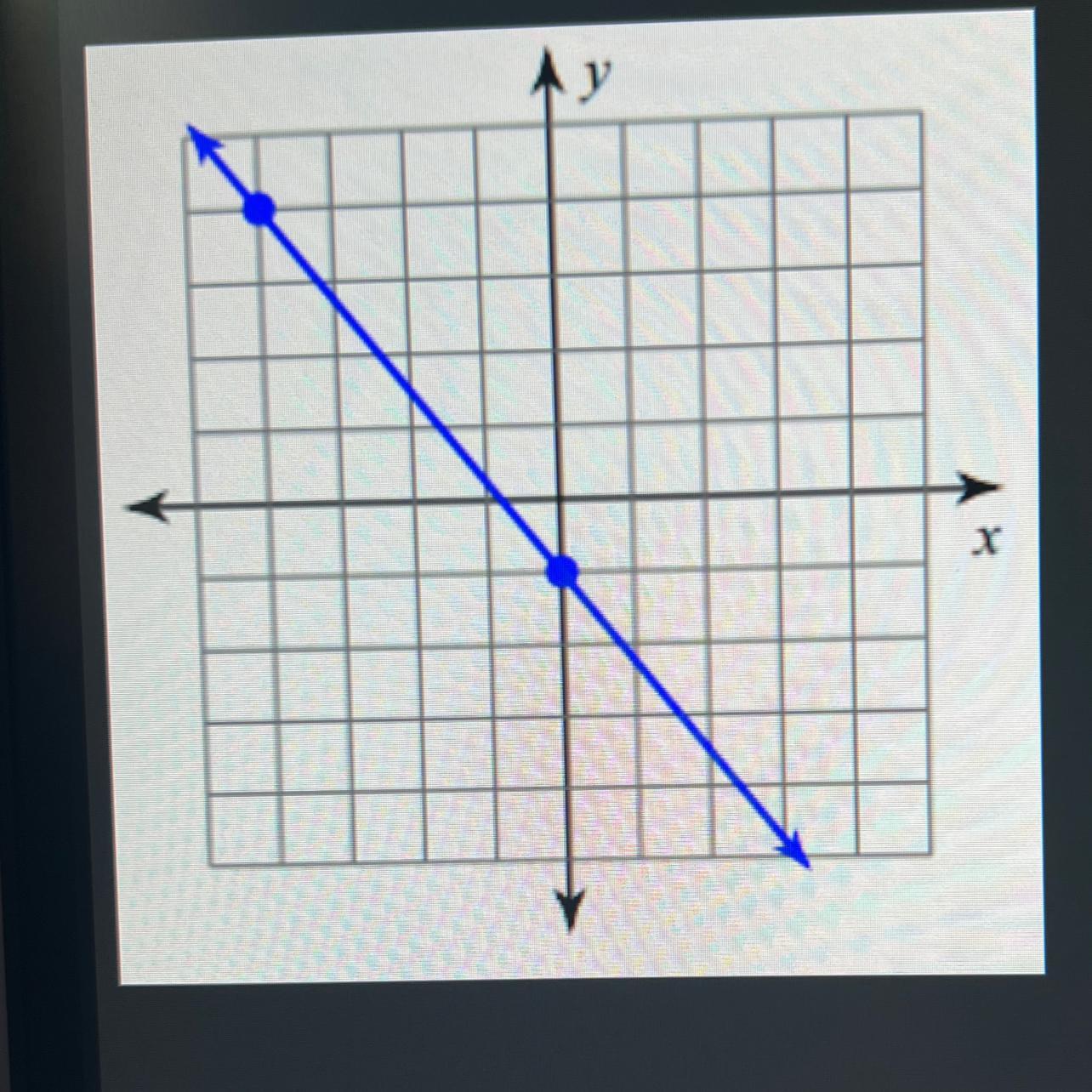
Answers
Answer:
-5/4
Step-by-step explanation:
Let \((x_1,y_1)=(-4,4)\) and \((x_2,y_2)=(0,-1)\). The slope of the line would be:
\(\displaystyle \frac{y_2-y_1}{x_2-x_1}=\frac{-1-4}{0-(-4)}=\frac{-5}{4}=-\frac{5}{4}\)
Answer: -5/4
Step-by-step explanation:
To find the slope between two points, you can use the formula:
Slope = (y2 - y1)/(x2 - x1)
Using the points (0, -1) and (-4, 4), we can substitute the coordinates into the formula:
slope = (4 - (-1))/(-4 - 0)
slope = (4 + 1)/(-4)
slope = 5/-4
Therefore, the slope between the two points is -5/4.
helppppppppp plssssssssss

Answers
A. Is the answer of this question
Due to renovations at her workplace, Lucía must move from her current office into a temporary office. Her current office is a square room of dimension xx feet. Her temporary office will be a rectangular room with a length 33 feet greater than her current office's length and a width 55 feet less than her current office's width. Which of the following expressions gives the difference between the area, in square feet, of Lucía's current office and the area, in square feet, of Lucía's temporary office?
A
2x+152x+15
B
2x-152x−15
C
-2x+15−2x+15
D
-8x-15−8x−15
E
8x+158x+15
Answers
Answer:
A. 2x + 15Step-by-step explanation:
Current office area:
x*x = x²Temporary office dimensions:
x + 3 and x - 5Temporary office area:
(x + 3)(x - 5) = x² - 2x - 15The difference is:
x² - (x²- 2x - 15) = x² - x² + 2x + 15 =2x + 15Correct choice is A
Yolanda is planning out her square vegetable garden. One side 8 feet. What 1 point
is the area? *
Answers
Answer:
64 feet
Step-by-step explanation: 8 x 8 = 64, we know to duplicate 8 since it is a Square Garden.
Hope this Helps!
Please help!!!
The purple shape is a dilation of the black shape. What is the scale factor or the dial action?

Answers
Answer:
I belive it would be 1/5. ;;;
Assume the random variable X has a binomial distribution with the given probability of obtaining a success. Find the following probability, given the number of trials and the probability of obtaining a success. Round your answer to four decimal places.
P(X≥10)
, n=14
, p=0.8
Answers
Using binomial distribution, P(X≥10)=0.8349
What is Binomial distribution?Binomial distribution is a discrete probability distribution which gives only two possible results on experiment which is success and failure.
\(P(X=x) = nC_{x} p^{x} (1-p)^{n-x}\), where \(nC_{x} = \frac{n!}{x!(n-x)!}\)
In this problem, given that n=14, p=0.8
The desired probability is,
P(X≥10) = P(X=10)+P(X=11)+P(X=12)+P(X=13)+P(X=14)
\(P(X=x) = nC_{x} p^{x} (1-p)^{n-x}\)
P(X=10)= \(14C_{10}(0.8)^{10} (1-0.8)^{14-10}\) = 0.1720
P(X=11) = \(14C_{11}(0.8)^{11} (1-0.8)^{14-11}\)=0.2501
P(X=12) = \(14C_{12}(0.8)^{12} (1-0.8)^{14-12}\) = 0.2501
P(X=13) = \(14C_{13}(0.8)^{13} (1-0.8)^{14-13}\) = 0.1539
P(X=14) = \(14C_{14}(0.8)^{14} (1-0.8)^{14-14}\) =0.0088
Then, P(X≥10)= 0.1720+0.2501+0.2501+0.1539+0.0088
Hence, P(X≥10) = 0.8349
Learn more about binomial distribution here:
https://brainly.com/question/29163389
#SPJ1
question attached as a file/picture .Options:a. a gain or a loss.b. a gain or a loss.

Answers
Given the negative numbers:
\(\begin{gathered} -33 \\ -125.68 \end{gathered}\)You need to remember that negative numbers are those numbers less than zero. Therefore:
\(\begin{gathered} -33<0 \\ \\ -125.68<0 \end{gathered}\)a. Given the phrase "-33 rushing yards in a football game", you know that the rushing yards are represented by a negative number and it is less than zero. Therefore, it indicates a loss.
b. Given the phrase "Stock market performance for the day: -125.68 points". You can also identify that it is less than zero, therefore, it lost -125.68 points.
Hence, the answers are:
a. Loss.
b. Loss.
Select all expressions that are equivalent to 3⁴.
A. 7
B. 4³
C. 12
D. 81
E. 64
F. 9²
Answers
Answer: D and F
Step-by-step explanation:
3 to the power of 4 means 3x3x3x3.
3x3 is 9
9x3 is 27
And 27x3 is 81
9 to the power of 2 means 9x9
9x9 equals 81
find the derivative of the function f(x) = 5(2 - x2)3
Answers
We will like to find the derivative of the function
\(f(x)=5(2-x^2)^3\)then
\(\begin{gathered} \frac{df}{dx}=\frac{d}{dx}\lbrack5(2-x^2)^3\rbrack \\ =5\frac{d}{dx}(2-x^2)^3 \\ =5\lbrack3(2-x^2)^2\frac{d}{dx}(2-x^2)\rbrack \\ =5\lbrack3(2-x^2)^2(-2x)\rbrack \\ =-30x(2-x^2)^2 \end{gathered}\)In this process we use the chain rule
\(\frac{d}{dx}\lbrack f(x)\rbrack^n=n\lbrack f(x)\rbrack^{n-1}\)to find the derivative of
\(\frac{d}{dx}(2-x^2)^3\)therefore
\(\frac{df}{dx}=-30x(2-x^2)^2\)10ft,10ft,4ft what is the area
Answers
Answer:
400 ft sq
Step-by-step explanation:
Area = Length x Width x Height
10 x 10 x 4
100 x 4
400
Have a great day!!
Please rate and mark brainliest!!
\left(a-b\right)\sqrt{\frac{2}{a^2-b^2}}
Answers
Answer:
\(\left(a-b\right)\sqrt{\frac{2}{a^2-b^2}}\)
=
\(\frac{ \sqrt{2} }{a + b} \)
Step-by-step explanation:
\(\left(a-b\right)\sqrt{\frac{2}{a^2-b^2}}\)
\((a - b)( \frac{ {2}^{ \frac{1}{2} } }{(a + b)(a - b)} )\)
\( \frac{(a - b)( {2}^{ \frac{1}{2} }) }{(a - b)(a + b)} = \frac{ \sqrt{2} }{a + b} \)
a car company wants to ensure its newest model can stop in 8 sec when traveling at 80 mph. if we assume constant acceleration, find the value of deceleration (in ft/sec2) that accomplishes this. (round your answer to two decimal places)
Answers
The 7.335 is the value of acceleration needed to achieve the condition that ensure its newest model can stop in 8 sec when traveling at 80 mph.
Explain the term constant acceleration?A change in speed that doesn't alter over time is referred to as a constant acceleration. A car's average acceleration stays constant at 20 mph per minute even if it increases its speed by 20 mph in one minute and another 20 mph the next.The car will move a maximum time 8 seconds when the brake is activated.
Initial velocity; u = 80 mph = (1.467 x 80) = 117.36 ft/s
Final velocity as it stops, v = 0 m/s
To find the car's deceleration, use the following kinematic equation.
v = u + 2at
0 = 117.36 + 2(a)(8)
a = -117.6/16 ft/s²
|a| = 7.335 ft/s²
Therefore, 7.335 is the value of acceleration needed to achieve the condition that ensure its newest model of car can stop in 8 sec when traveling at 80 mph.
To know more about the constant acceleration, here
https://brainly.com/question/28693744
#SPJ4
what is the answer of this question?

Answers
Answer:
Its B.
Step-by-step explanation:
Because \(11^{2}\) + \(12^{2}\) does not equal \(15^{2}\)
121 + 144 \(\neq\) 225
265 \(\neq\) 225
50 Points! Multiple choice algebra question. Photo attached. Thank you!

Answers
Answer:
B. 3188.5 cubic inches.
Step-by-step explanation:
The volume of a cone is calculated using the following formula:
Volume = (1/3) * π * r² * h
Where:
π is the mathematical constant pi, approximately equal to 3.14.r is the radius of the base of the cone.h is the height of the cone.In this problem, we are given that r = 17 inches and S.h = 20 inches.
First we need to find height h.
py using Pythagorous theorem,we get
c²=a²+b²
here c= slight height and a is radius
20²=17²+b²
20²-17²=b²
111=b²
b=√(111)
Plugging these values into the formula, we get:
Volume = ⅓*π* 17² *√(111) = 3188.5 cubic inches
Therefore, the volume of the cone is 3188.5 cubic inches.
Question 6 of 19 Step 1 of 1 Suppose that quiz scores in a beginning statistics class have a mean of 7.1 with a standard deviation of 0.4. Using Chebyshev's Theorem, state the range in which at least 75% of the data will reside. Please do not round your answers. Answer(How to Enter) 4 Points to
Answers
Suppose that quiz scores in a beginning statistics class have a mean of 7.1 with a standard deviation of 0.4, the range in which at least 75% of the data will reside is from 6.3 to 7.9.
Chebyshev's Theorem is a statistical tool that provides a range for how much data is likely to fall within a certain number of standard deviations from the mean.
Specifically, it tells us that, for any set of data, no matter how it is distributed, at least 1 - (1/k^2) of the data will fall within k standard deviations from the mean, where k is any positive number greater than 1.
In this case, we want to find the range in which at least 75% of the data will reside. We can use Chebyshev's Theorem to determine the minimum value of k that will give us this range. We know that at least 75% of the data should fall within two standard deviations from the mean, so we can set k = 2.
Using Chebyshev's Theorem, we can say that at least 1 - (1/2^2) = 75% of the data will fall within 2 standard deviations from the mean. The standard deviation is 0.4, so two standard deviations would be 2 * 0.4 = 0.8.
To learn more about range click on,
https://brainly.com/question/30657711
#SPJ4