5. Order from least to greatest.
4996,
10
48%
3. 41
0.408,
7100
Answers
Answer:
0.408
48%
3.41
10
4996
7100
Step-by-step explanation:
Answer:
It should be 0.408, 48%( which is equal to 0.48), 3.41,10,4996,and 7100
Step-by-step explanation:
Related Questions
What is the slope of a line perpendicular to the line whose equation is 6x+y=-5.Fully simplify your answer.
Answers
Answer:
The slope is 1/6.
Step-by-step explanation:
The slope of the given equation is -6. Perpendicular lines have negative reciprocal slopes.
use the law of exponents to simplify the following expression

Answers
Answer:
5x⁴
Step-by-step explanation:
10x⁸÷2x⁴=
5x⁴
Tyee goes out to lunch. The bill, before tax and tip, was $14.20. A sales tax of 6% was added on. Tyee tipped 18% on the amount after the sales tax was added. How much tip did he leave? Round to the nearest cent.
Answers
Answer:
$4.09
Step-by-step explanation:
14.20+6% of 14.20 = 15.05
118% of 15.05= 18.29
18.29-14.20=4.09
In one day, a store sold 2/3 as many DVDs as Blu-Ray discs. the total number of DVDs Blu-ray discs sold that day was 280, how many DVDs were sold?
Answers
Answer: Let's start by representing the number of Blu-Ray discs sold as x.
According to the problem, the store sold 2/3 as many DVDs as Blu-Ray discs. So the number of DVDs sold is 2/3 of x, or (2/3)x.
We also know that the total number of DVDs and Blu-Ray discs sold was 280. So we can set up an equation:
(2/3)x + x = 280
To solve for x, we can simplify the equation by combining like terms:
(5/3)x = 280
Multiplying both sides by 3/5, we get:
x = 168
So the number of Blu-Ray discs sold was 168.
To find the number of DVDs sold, we can use the expression we derived earlier:
(2/3)x = (2/3) * 168 = 112
Therefore, the store sold 112 DVDs on that day.
Step-by-step explanation:
A large soup pot holds 20 quarts of soup. What could be its volume in liters? (Note a
liter is slightly larger than a quart)
a. 7.57
b. 19
c. 21
d. 75.7
Answers
Answer:
a
because it is math
simple math
VERY simple math
when group a loses an item or items to group b even though group a's population grew at a faster rate than group b's, the _______ paradox occurs.
Answers
When Group A loses an item or items to Group B even though Group A's population grew at a faster rate than Group B's, the Simpson's Paradox occurs.
This statistical anomaly happens when a trend appears in different groups of data, but disappears or reverses when the groups are combined. It is crucial to consider the context and variables involved when analyzing data, as the Simpson's Paradox may lead to incorrect conclusions if only aggregate data is examined.
This paradox serves as a reminder to always investigate the underlying factors that may influence statistical results.
Learn more about Simpson's paradox at
https://brainly.com/question/31679249
#SPJ11
Elliot makes and sells key chains. His profit depends on what price he charges for a
key chain.
He writes the expression (x - 10) (60 - 3x) to represent his profit based on the
price per key chain, x.
Enter Elliot's average change in profit for two different sections of the graph.

Answers
When charging $15 for a key chain, it is discovered that his maximum profit is $75 using the vertex of the quadratic function.
The vertex of a quadratic equation,
A quadratic equation is given by, \(ax^{2} +bx +c\)
The vertex is given by \(A (x_{1} ,y_{1} )\)
\(x_{1} = \frac{-b}{2a}\\ \\y_{1} = \frac{-b^{2} +4ac }{4a}\)
Considering the coefficient a, we have that:
If a < 0, the vertex is a maximum point.
If a > 0, it will be a minimum point.
The function given is (x -10 ) (60 -3x)
f(x) = (x -10 ) (60 -3x) = 60x -3\(x^{2}\) -600 +30x = -3\(x^{2}\) +90x -600
So, here a = -3, b = 90 and c = -600
So,
\(x_{1} = \frac{-b}{2a}\\ \\x_{1} = \frac{-90}{2*(-3)} = 15\)
\(y_{1} = \frac{-b^{2} +4ac }{4a} = \frac{(-90)^{2} + 4*(-3)*(-600) }{4*(-3)} = 75\)
Hence, He can make up to $75 in profit when he charges $15 for a key chain.
To read more about quadratic equations, visit https://brainly.com/question/17177510
#SPJ1
Which of the binomials below is a factor of this trinomial? 4x2 + 12x + 9
A. 2x-3
B. 2x-1
C. 2x+1
D. 2x+3
Answers
Answer:
d-2x-3
Step-by-step explanation:
The factor of the trinomial will be (2x + 3) and (2x + 3). Then the correct option is D.
What is a factorization?It is a method for dividing a polynomial into pieces that will be multiplied together. At this moment, the polynomial's value will be zero.
The trinomial is given below.
⇒ 4x² + 12x + 9
Then the factor of the trinomial will be
⇒ 4x² + 12x + 9
⇒ 4x² + 6x + 6x + 9
⇒ 2x(2x + 3) + 3(2x + 3)
⇒ (2x + 3)(2x + 3)
⇒ (2x + 3)²
Then the correct option is D.
More about the factorization link is given below.
https://brainly.com/question/6810544
#SPJ2
What makes composing functions different from doing an arithmetic operation of two functions such as adding or dividing them? (please help!)
Answers
The resulting function may also have a different domain and Range than the original functions.
Composing functions is different from doing an arithmetic operation of two functions such as adding or dividing them in several ways.
First, it's worth noting that both operations involve working with functions, but in different ways. Composing FunctionsIn mathematics, a function composition refers to applying one function to the result of another function. This is usually written as follows:(f∘g)(x) = f(g(x))
Here, (f∘g) is the composite function of f and g. This means that the output of the function g is used as input for the function f to obtain the final result.
The order of the composition matters in the sense that the function g is applied first followed by the function f. Composing functions is different from arithmetic operations of two functions because it produces a new function, not a value. Additionally, the domain and range of the resulting composite function depend on the domains and ranges of the original functions. In other words, the composition of two functions is only possible if the domain of the second function is the same as the range of the first function.
Arithmetic Operations of Two Functions When two functions are added, subtracted, multiplied, or divided, the result is a new function that can be evaluated for a given value. For example, if f(x) = x^2 and g(x) = x, then f + g = x^2 + x, which is a new function. To evaluate this function, one needs to plug in a value for x.
Arithmetic operations of two functions are different from composing functions in that they don't produce a new function; instead, they produce a value.
Additionally, arithmetic operations can be performed between functions with different domains and ranges, unlike function composition.
The resulting function may also have a different domain and range than the original functions.
For more questions on Range .
https://brainly.com/question/30389189
#SPJ8
which action by the group leader demonstrates effective leadership?
Answers
Effective leadership can be demonstrated in many different ways, but here are a few examples of actions that may indicate effective leadership by a group leader:
1. Clear communication: A group leader who communicates clearly and effectively with their team is more likely to build trust and respect among the group.
2. Empathy and emotional intelligence: A leader who demonstrates empathy and emotional intelligence can help build a positive team culture by understanding and acknowledging the feelings and needs of their team members.
3. Delegation and empowerment: An effective leader knows how to delegate tasks and responsibilities to team members in a way that maximizes their strengths and abilities, while also providing support and guidance as needed.
4. Leading by example: A leader who sets a positive example for their team by modeling the behaviors and attitudes they want to see in their team is more likely to earn respect and trust from their team members.
5. Strategic thinking: A leader who is able to think strategically and make informed decisions based on data and evidence can help steer their team towards success.
Know more about leadership here:
https://brainly.com/question/1232764
#SPJ11
what is the value of x? 5 60 30 marking brainliest and giving thanks to all!!!

Answers
this is 90 60 30 formula for example
90 meet 2x
30 meet x
and
60 meet x√3
so 90 meet 5
30 meet 5/2=2.5
and 60 meet 2.5√3
so the answer is 2.5
Answer:
2.5
Step-by-step explanation:
\(\sin 30\degree = \frac{x}{5}\\\therefore x = 5\sin 30\degree\\\therefore x = 5 \times \frac{1}{2}\\\therefore x = 2.5\)
Please help - geometric progression

Answers
Answer:
\(\frac{2560}{93}\)
Step-by-step explanation:
\(1+2+3+\cdots+10=\frac{10+1}{2}(10)=55 \\ \\ 1+\frac{1}{2}+\frac{1}{4}+\cdots+\frac{1}{512}=\frac{1(1-(1/2)^{10}}{1-(1/2)}=2(1-(1/2)^{10} \\ \\ \frac{55}{2(1-(1/2)^{10}}=\frac{2560}{93}\)
I’m jacks class, 18 of the students are tall and 10 are short. In Michael’s class 54 students are tall and 30 short which class has a higher ratio of tall to short students.
Answers
Answer:
neither they are the same value of ratio
Step-by-step explanation:
18:10 - jacks class
54:30- micheal’s class
18:10
x3 x3
54:30
Meaning the ratio is the exact same value
Hopes this helps please mark brainliest
If m
15 points thanks you :)


Answers
Answer:
48
Step-by-step explanation:
check the attached file

Use a double integral to find the area of the region inside the cardioid r=1+cosθ and outside the circle r=3cosθ.
Answers
The area of the region inside the cardioid and outside the circle is 3π/2 square units.
The area of the region inside the cardioid r=1+cosθ and outside the circle r=3cosθ using a double integral, follow these steps:
1. Determine the bounds of integration for θ: Find where the cardioid and circle intersect by setting r equal for both equations: (1+cosθ) = 3cosθ. Solve for θ, which results in θ = 0 and θ = π.
2. Set up the double integral: The area of the region can be found using the double integral of the difference between the two polar functions with respect to r and θ: Area = ∬(1+cosθ - 3cosθ) rdrdθ.
3. Determine the bounds of integration for r: The lower bound for r is the circle r=3cosθ, and the upper bound is the cardioid r=1+cosθ.
4. Integrate with respect to r: ∫[∫(1+cosθ - 3cosθ) rdr]dθ from r=3cosθ to r=1+cosθ. This results in: [1/2(r^2)] evaluated from r=3cosθ to r=1+cosθ.
5. Plug in the limits of integration for r: [(1/2)((1+cosθ)^2) - (1/2)(3cosθ)^2]dθ.
6. Integrate with respect to θ: ∫[(1/2)((1+cosθ)^2) - (1/2)(3cosθ)^2] dθ from θ=0 to θ=π.
7. Evaluate the integral: After integrating and evaluating the limits, you will find that the area of the region inside the cardioid and outside the circle is 3π/2 square units.
To know more about cardioid refer here:
https://brainly.com/question/29556891#
#SPJ11
what is 7/10 of the coordinates (-4,-6) (12,5)
Answers
7/10 of the coordinates (-4,-6) (12,5) is given as (11.2, 1.7)
How to solve for 7/10 0f (-4,-6) (12,5)
we have -4 + 12 = 16
7/10 of 16
= 11.2
11.2 + -4 =
7.2 for the x coordinate
from -6 to 5 = 11 units
7/10 * 11 = 7.7
7.7 - 6 = 1.7
hence the point 7/10 from the coordinates a to b = (11.2, 1.7)
Read more on coordinates here:
https://brainly.com/question/17206319
#SPJ1
I NEED HELP ON THIS
(see photo below for questions)
v

Answers
Answer:
∠4 = ∠5 = ∠8 = ∠1 = 140°∠2 = ∠3 = ∠6 = ∠8 = 40°Step-by-step explanation:
Given angle 1 = 140°, you want the measures of the other numbered angles where a transversal crosses parallel lines.
ReasonsWhere a transversal crosses parallel lines, corresponding angles are congruent.
Wherever lines cross. vertical angles are congruent, and linear pairs are supplementary.
These reasons together tell you all the obtuse angles are congruent, and all the acute angles are congruent. The obtuse and acute angles are supplementary.
Application∠1 = ∠4 = ∠5 = ∠8 = 140° . . . . . . given
∠2 = ∠3 = ∠6 = ∠7 = 40° . . . . . . done for you
__
Additional comment
The angles are also named according to where pairs of angles are found.
alternate — on opposite sides of the transversalconsecutive, or same side — on the same side of the transversalinterior — between the parallel linesexterior — outside the parallel linescorresponding — in the same direction from the point of intersection (for example, angles 1 and 5 are both northwest of their vertices, hence corresponding)Various theorems describe the congruent/supplementary status of pairs of angles using these names:
if the lines are parallel, then corresponding angles are congruent; if the lines are parallel, then consecutive exterior angles are supplementary; ....In general, the converses of these theorems are also true. If corresponding angles are congruent, then the lines are parallel.
Conchita starts a savings account. She deposits $100 from her parents. After that, she
deposits $10 each month. Write an algebraic expression to give the amount of money she
has saved after m months.
Answers
Answer:
$100 + $10m
Step-by-step explanation:
A = Account Balance = 100
After M months
A = $100 + $10m
Help meee due tomorrow What is the decimal equivalent to 19/25
A.0.19
B.0.76
C.0.25
D.0.63
class Math
Answers
Answer:
The correct is the little (B) 0.76
paige just finished a road trip where she visited the following square pyramids: the bent pyramid and the red pyramid. the table below shows the approximate dimensions of the two pyramids. dimensions of pyramids base side length height bent pyramid 619 feet 332 feet red pyramid 722 feet 341 feet paige has to write a paper on volume for school and needs some help. what is the difference in volume of the two pyramids, rounded to the nearest cubic foot?
Answers
The difference in volume between the two pyramids is 12,371,740 cubic feet.
To find the volume of a square pyramid, you use the formula :
V = (1/3)Bh, where B is the area of the base and h is the height.
Using the dimensions given in the table, we can calculate the volumes of the two pyramids:
- Volume of Bent Pyramid = (1/3)(619 feet * 619 feet)(332 feet) = 26,384,053.33 cubic feet
- Volume of Red Pyramid = (1/3)(722 feet * 722 feet)(341 feet) = 38,755,793.33 cubic feet
To find the difference in volume between the two pyramids, we subtract the smaller volume from the larger volume:
38,755,793.33 - 26,384,053.33 = 12,371,740 cubic feet.
Rounding to the nearest cubic foot, the difference in volume between the two pyramids is 12,371,740 cubic feet.
To know more about volumes refer here :
https://brainly.com/question/17615619#
#SPJ11
Nicole is 56 inches tall and has an 84 inch shadow. Julie is standing next to Nicole and has a 96 inch shadow. How tall is Julie?
Answers
Answer:
56+12=68. 68 inches
Step-by-step explanation:
julie‘s shadow is 12 inches taller than Nicole’ so you would just add 12 to 56.
Consider these functions: Two firms, i = 1, 2, with identical total cost functions: ; Market demand: P= 100 - Q = 100 – 9,- 9. (9, could differ from q, only if costs differ.); Marginal cost: MC = 4 + q. a. Please calculate the price, quantity, and profit for firm 1 and 2 if firm 1 could have for any price that firm 2 charges?
Answers
Firm 1 and Firm 2 will produce the same quantity and charge the same price in this scenario.
To determine the price, quantity, and profit for Firm 1 and Firm 2, we need to analyze the market equilibrium. In a competitive market, the price and quantity are determined by the intersection of the market demand and the total supply.
Market Demand:
The market demand is given by the equation P = 100 - Q, where P represents the price and Q represents the total quantity demanded in the market.
Total Cost:
Both firms have identical total cost functions, which are not explicitly provided in the question. However, we can assume that the total cost function for each firm is given by TC = C + MC * Q, where TC represents the total cost, C represents the fixed cost, MC represents the marginal cost, and Q represents the quantity produced by the firm.
Given that the marginal cost is MC = 4 + Q, we can rewrite the total cost function as TC = C + (4 + Q) * Q.
Market Equilibrium:
To find the market equilibrium, we set the market demand equal to the total supply. In this case, since Firm 1 can charge any price that Firm 2 charges, both firms will produce the same quantity and charge the same price.
Market Demand: P = 100 - Q
Total Supply: QS = Q1 + Q2 (quantity produced by Firm 1 and Firm 2)
Setting the market demand equal to the total supply, we have:
100 - Q = Q1 + Q2
Since Firm 1 and Firm 2 have identical total cost functions, they will split the market equilibrium quantity equally. Therefore, Q1 = Q2 = Q/2.
Substituting Q1 = Q2 = Q/2 into the equation 100 - Q = Q1 + Q2, we get:
100 - Q = Q/2 + Q/2
100 - Q = Q
Solving this equation, we find Q = 50. Thus, both Firm 1 and Firm 2 will produce 50 units of output.
Price Calculation:
To calculate the price, we substitute the quantity (Q = 50) into the market demand equation:
P = 100 - Q
P = 100 - 50
P = 50
Therefore, both Firm 1 and Firm 2 will charge a price of 50.
Profit Calculation:
To calculate the profit for each firm, we subtract the total cost from the total revenue. The total revenue for each firm is given by the product of the price (P = 50) and the quantity (Q = 50).
Total Revenue (TR) = P * Q = 50 * 50 = 2500
The total cost function for each firm is TC = C + (4 + Q) * Q. Since the fixed cost (C) is not provided, we cannot determine the profit explicitly. However, we can compare the profit of Firm 1 and Firm 2 if their total costs are the same.
Since both firms have identical total cost functions, they will have the same profit when their costs are the same. If their costs differ, then the firm with lower costs will have higher profits.
Overall, both Firm 1 and Firm 2 will produce 50 units of output, charge a price of 50, and their profits will depend on their total costs, which are not explicitly provided in the question.
For more questions like Demand click the link below:
https://brainly.com/question/29761926
#SPJ11
Geometry problem....

Answers
Answer:
Step-by-step explanation:
24/x = 28/(32 - x) Cross multiply
24 * (32 - x) = 28x Remove the brackets.
768 - 24x = 28x Add 24x to both sides
768 = 28x + 24x
768 = 52x
52x = 768 Divide by 52
x = 768/52
x = 14.77
AB = 32 - 14.77
AB = 17.23
there are 45 students In a class if 60% of them are girls and 40% of them are boys find the number of girls and boys
Answers
Answer:
27 girls and 18 boys
Step-by-step explanation:
you need to divide the 45 pupils into 60 and 40 percent to
find the slope of the line through the given points 4,2 and 6,4
Answers
Answer:
2/2 = 1
Step-by-step explanation:
Slope intercept equation:
y2 - y1 / x2 - x1 = slope
write an if statement that assigns 10000 to the variable bonus if the value of the variable goodssold is greater than 500000
Answers
The if statement assigns a value of 10000 to the variable "bonus" if the value of the variable "goodssold" exceeds 500000.
To achieve this, we can use an if statement in programming. An if statement allows us to conditionally execute a block of code based on a specified condition. In this case, the condition is whether the value of the variable "goodssold" is greater than 500000. If the condition evaluates to true, the code inside the if statement will be executed, and the variable "bonus" will be assigned a value of 10000.
Here's an example of how the if statement can be written in Python:
if goodssold > 500000:
bonus = 10000
In this code snippet, the variable "goodssold" represents the number of goods sold, and we compare its value to 500000 using the greater than operator (>). If the condition is true, the code inside the if statement is executed, and the variable "bonus" is assigned a value of 10000. If the condition is false, the code inside the if statement is skipped, and the variable "bonus" retains its previous value (if any).
By using this if statement, we can dynamically assign a bonus of 10000 to the variable "bonus" based on the value of the variable "goodssold" being greater than 500000. This allows for flexible and conditional handling of the bonus calculation in the program.
Learn more about statement here:
https://brainly.com/question/30483936
#SPJ11
Find the measure of the exterior Angle1 (I’m a bit confused on how exterior angles work)
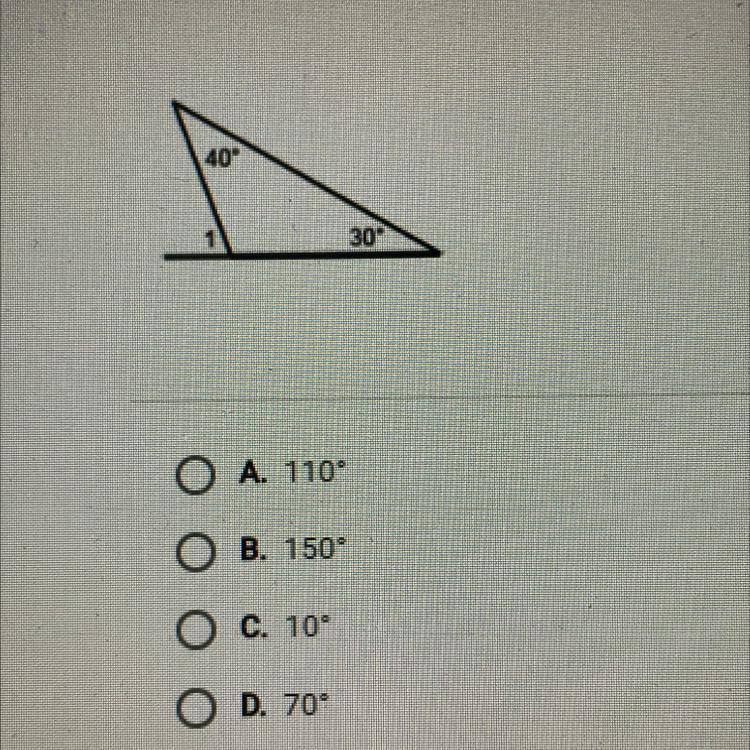
Answers
Answer:
70
Step-by-step explanation:
I would do 40 + 30 = 70
180-70 = 110
110 is the last angle bc all angles add to 180 in a triangle
Then 180 - 110 = 70 for angle 1 because their supplementary
I don't know if you could just add the 2 inside angles but I would do it this way to be safe until I know for sure.
Angles H and K are alternate exterior angles formed by two parallel lines cut by a transversal. If m∠H=(2x+7)°m∠H=(2x+7)° and m∠K=(5x−8)°m∠K=(5x-8)° , find the value of x .
PLEASE SOMEBODY HELP ME!!!
Answers
Based on the alternate exterior angles theorem, the value of x is: 5.
What is the Alternate Exterior Angles Theorem?According to the alternate exterior angles theorem, when two parallel lines are cut by a transversal, the alternate exterior angles are congruent. Therefore, if m∠H = (2x+7)° and m∠K = (5x−8)°, we can set up the equation:
(2x + 7)° = (5x − 8)°
Solving for x we get:
2x + 7 = 5x - 8
Subtracting 2x from both sides:
2x + 7 - 2x = 5x - 8 - 2x
7 = 3x - 8
Adding 8 to both sides:
15 = 3x
Dividing both sides by 3:
x = 5
So the value of x is 5.
Learn more about the alternate exterior angles on:
https://brainly.com/question/26111088
#SPJ1
Find the general solution of the differential equation y"-9y'+20y=0
Answers
Given differential equation is y"-9y'+20y=0We can write this equation asy²-9y+20y=0Here, a = 1, b = -9, and c = 20Now, we have to find the roots of this equation.
Now, let us find the value of the discriminant. b²-4ac= (-9)²-4(1)(20)= 81-80= 1Since the value of the discriminant is greater than zero, therefore, we have two real and distinct roots for this equation.Roots are given by the quadratic formula.x= (-b±√(b²-4ac))/2aOn substituting the values of a, b, and c we get,x = (9±√1)/2Now,x1= 5x2= 4/1These roots give two linearly independent solutions as follows: y1=e^5t and y2=e^4tTherefore, the general solution to the differential equation is:y=c1e^5t+c2e^4tWhere c1 and c2 are constants.
To know more about differential, visit:
https://brainly.com/question/33188894
#SPJ11
The given differential equation is y"-9y'+20y=0.
Let us use the characteristic equation to solve this differential equation.
The characteristic equation of y"-9y'+20y=0 isr² - 9r + 20 = 0.
Solve for r by factoring the characteristic equation(r - 5)(r - 4) = 0.
Therefore, r = 5 and r = 4.
Thus, the general solution of the differential equation y"-9y'+20y=0 isy(x) = c₁e⁴x + c₂e⁵x
where c₁, c₂ are constants.
To know more about characteristic equation, visit:
https://brainly.com/question/31428714
#SPJ11
a school librarian wanted to estimate the proportion of students in the school who had read a certain book. the librarian sampled 50 students from the senior english classes, and 35 of the students in the sample had read the book. have the conditions for creating a confidence interval for the population proportion been met? responses yes, because the sample was selected at random. yes, because the sample was selected at random. yes, because sampling distributions of proportions are modeled with the normal model. yes, because sampling distributions of proportions are modeled with the normal model. yes, because the sample is large enough to satisfy the normality conditions. yes, because the sample is large enough to satisfy the normality conditions. no, because the sample is not large enough to satisfy the normality conditions. no, because the sample is not large enough to satisfy the normality conditions. no, because the sample was not selected using a random method.
Answers
The normality assumption is valid.
The librarian can proceed to create a confidence interval for the population proportion of students in the school who have read the book.
The school librarian has a goal of estimating the proportion of students in the school who have read a particular book. The librarian sampled 50 students from the senior English classes, and out of those 50 students, 35 of them had read the book.
The question at hand is whether the conditions for creating a confidence interval for the population proportion have been satisfied.
Firstly, it is essential to establish that the sample was selected at random.
According to the question, this has been done.
It is a crucial condition because it helps to avoid bias in the sample.
If the sample had not been selected at random, there would be a risk of under- or over-representing certain groups, leading to an inaccurate estimation of the proportion of students who have read the book.
Secondly, sampling distributions of proportions are modeled with the normal model.
This condition has been met because the sample size (50 students) is greater than or equal to 30.
When the sample size is this large, the sampling distribution of proportions can be approximated to the normal distribution.
The normality assumption is valid when the sample size is large enough to satisfy the rule of thumb of np≥10 and nq≥10.
Thus, both conditions for creating a confidence interval for the population proportion have been met.
The sample was selected at random, and the sample size is greater than or equal to 30.
For similar question on assumption.
https://brainly.com/question/29672185
#SPJ11