-5(x+2)=-20
Help me find X
Answers
Answer:
x=2 :D
Step-by-step explanation:
first divide by -5 on both sides to get x+2=4 then subtract 2, and get x=2
Answer:
I'm pretty sure its 2
Step-by-step explanation:
I did the math
Related Questions
Builtrite has calculated the average cash flow to be $14,000 with a standard deviation of $5000. What is the probability of a cash flow being between than $16,000 and $19,000 ? (Assume a normal distribution.) 16.25% 18.13% 23.90% 2120%
Answers
The correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.
We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.
The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.
First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.
z1 = 2,000 / 5,000 = 0.4.
Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.
z2 = 5,000 / 5,000 = 1.
Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.
Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.
Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.
Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.
So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
The probability of a cash flow between $16,000 and $19,000 is approximately 18.59%.
To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.
We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.
The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.
First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.
z1 = 2,000 / 5,000 = 0.4.
Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.
z2 = 5,000 / 5,000 = 1.
Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.
Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.
Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.
Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.
So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
Three eighths of the 48 roses were red. (a) How many roses were red? (b) How many roses were not red? (c) What fraction of the roses were not red?
Answers
Answer:
A. 18 roses were red.
B. 30 roses were not red.
C. 5/8 were not red.
Step-by-step explanation:
In order to do this question, we first need a calculator. Then, we take three eighths and divide them on the calculator to get:
3 divided by 8 = 0.375.
Then, on the calculator again, we take the 48 roses and find the percentage of the roses that were red, by multiplying it by 0.375:
0.375 x 48 = 18.
A. 18 roses were red.
Now, for the next question, how many roses were not red. We take the 48 roses and subtract it from the roses that were red, which were 18 roses:
48 - 18 = 30.
B. 30 roses were not red.
Now, to find the fraction of the roses that weren't red. We take the 30 roses that weren't red and divide it by the total amount of 48 roses:
30 divided by 48 = 0.625.
In order to make 0.625 into a fraction, we take the higher, but lowest 100th place we can make for 0.625:
625/1,000.
Now, we simplify it:
625 divided by 5 = 125
1,000 divided by 5 = 200
Now, we have 125/200.
Simplify more:
125 divided by 5 = 25
200 divided by 5 = 40
Once more:
25 divided by 5 = 5
40 divided by 5 = 8
Our final fraction is 5/8.
C. The fraction of the roses that were not red are 5/8.
May I have Brainliest please? My next rank will be the highest one: A GENIUS! Please help me on this journey to become top of the ranks! I would really appreciate it, and it would make my day! Thank you so much, and have a wonderful rest of your day!
The table shows the side length and approximate area of an octagonal stop sign. Area of a stop sign a 2-column table with 5 rows. The first column is labeled side length (inches), x with entries 5, 10, 15, 20, 25. The second column is labeled area, f(x) with entries 120; 480; 1,080; 1,920; 3,000. Which function can be used to compute the approximate area, in square inches, of a stop sign if it has a side length of x inches? f(x) = 4. 8x2 f(x) = 4x2 f(x) = (4. 8)x f(x) = (4)x.
Answers
f(x) = 4. 8x² function can be used to compute the approximate area, in square inches, of a stop sign if it has a side length of x inches.
What do function and example exactly mean?A function, which produces single output from either a single input, is an illustration of a rule. Alex Federspiel was contacted to collect the image. An illustration of this is the equation y=x2. For each input of x, there is simply one output of y. Considering that x is actually the input value, we would claim that y is just a rational number.
Briefing:area = (# of sides * side length^2) / [4 * tan (180/n)]
area = (8 * x^2) / 4 * tan (22.5)
area = 8 x^2 / (4 * 0.41421)
area = 8 x^2 / 1.65684
area = 4.8 x^2
To know more about Function visit:
https://brainly.com/question/9554035
#SPJ4
a rectangular piece of metal is in longer than it is wide. squares with sides in long are cut from the four corners and the flaps are folded upward to form an open box. if the volume of the box is inâ, what were the original dimensions of the piece ofâ metal?
Answers
The original dimensions of the metal piece are:
L = 4 * V^(2/3) * t / (2 * V^(2/3) + 1) + tW = 4 * V^(2/3) * t / (2 * V^(2/3) + 1)Metal Box Volume CalculationLet's say the length of the original metal piece is L and the width is W. The squares that are cut from the corners have sides of x. After the flaps are folded upward, the resulting dimensions of the box are L - 2x and W - 2x. The volume of the box is given as:
V = (L - 2x) * (W - 2x) * xAnd it is equal to V = x³.So, we can write:(L - 2x) * (W - 2x) * x = x³
Expanding the left side:LWx - 2Lx² - 2Wx² + 4x³ = x³
LWx - 2Lx² - 2Wx² = 0
LW = 2(L + W)x²
Dividing both sides by x²:LW / x² = 2(L + W)
Since the volume of the box is given as x³, we can substitute x = V^(1/3):LW / V^(2/3) = 2(L + W)
Rearranging:LW = 2(L + W) * V^(2/3)
LW = 2V^(2/3) (L + W)
LW = 2 * V^(2/3) * (L + W)
Since the original metal piece was longer than it was wide (L > W), we have:L = W + t for some t > 0.
Substituting this into the above equation:W (W + t) = 2 * V^(2/3) * (W + t + t)
Expanding:W² + Wt = 2 * V^(2/3) * (2t + W)
W² = 2 * V^(2/3) * 2t + 2 * V^(2/3) * W
W² = 4 * V^(2/3) * t + 2 * V^(2/3) * W
Dividing both sides by (2 * V^(2/3) + 1):W^2 / (2 * V^(2/3) + 1) = 4 * V^(2/3) * t / (2 * V^(2/3) + 1) + 2 * V^(2/3)
* W / (2 * V^(2/3) + 1)
W * (2 * V^(2/3) + 1) = 4 * V^(2/3) * t + 2 * V^(2/3) * W
W = 4 * V^(2/3) * t / (2 * V^(2/3) + 1)
L = W + t = 4 * V^(2/3) * t / (2 * V^(2/3) + 1) + t
So the original dimensions of the metal piece are:L = 4 * V^(2/3) * t / (2 * V^(2/3) + 1) + t
W = 4 * V^(2/3) * t / (2 * V^(2/3) + 1)
Learn more about Metal Box Volume Calculation here:
https://brainly.com/question/17330556
#SPJ4
What is the slope of a line that passes through the points (9,8) and (2,3)?
Answers
The slope of the line that passes through the points (9,8) and (2,3) is 5/7.
What is a slope in a graph?The slope of a line in a graph is a measure of its steepness or slant. It is defined as the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line. In mathematical terms, the slope of a line can be represented as the difference in the y-coordinates of two points on the line divided by the difference in the x-coordinates of the same two points.
The slope of a line passing through two points (x1, y1) and (x2, y2) can be found using the formula:
slope = (y2 - y1) / (x2 - x1)
Plugging in the given points, we get:
slope = (3 - 8) / (2 - 9) = -5 / -7 = 5/7
So, the slope of the line that passes through the points (9,8) and (2,3) is 5/7.
To know more about ratio, visit:
https://brainly.com/question/13419413
#SPJ1
QUICK whoever gives correct answer Will get brainliest

Answers
Answer:
Slope can be found by determining the ratio of the rise (vertical change) to the run (horizontal change).
In this case miles is the rise, and 3 hours is the run
It should rise 12 and go over 3
I cannot really make out what's on your screen but it's likely it would be D.
The line has to pass 3, it cannot be off 3 by a bit.
And it should be lower than 20 because it rises 12.
What is the area of triangle ABC if a = 7, c = 11, and B = 55°?
Round the answer to the nearest hundredth.
Answers
The area of the triangle is 31.54 square units
How to determine the area of the triangleFrom the question, we have the following parameters that can be used in our computation:
We have the following values
a = 7 units
c = 11 units
B = 55 degrees
The area of the triangle is calculated using the following area formula
Area = 1/2absin(C)
Substitute the known values in the above equation, so, we have the following representation
Area = 1/2 * 7 * 11 * sin(55 degrees)
Evaluate
Area = 31.54
Hence, the area is 31.54 square units
Read more about area at
brainly.com/question/25292087
#SPJ1
The table shows the ages of players on a football team.
Age
Frequency
a) Work out the mean age of the team.
Round your answer to 1 decimal place.
19
2.
20
3
21
1
b) A new player joins the team and raises
the mean age to 22.
22
4
23
1
Work out the age of this new player.
Answers
Answer: A) 20.9 ; B) 34years
Step-by-step explanation:
Given the following :
AGE (X) - - - - - - - 19 - -20 - - - 21 - - - 22 - - - 23
FREQUENCY (F) - 2 - - 3 - - - - 1 - - - - 4 - - - - 1
A)
MEAN(X) = [AGE(X) × FREQUENCY (F)] ÷ SUM OF FREQUENCY
F*X = [(19 * 2) + (20 * 3) + ( 21 * 1)+(22 * 4)+(23 * 1)]
= 38 + 60 +21 + 88 + 23 = 230
SUM OF FREQUENCY = 2 + 3 + 1 + 4 + 1= 11
MEAN(X) = 230 / 11
X = 20.9
B)
WHEN A NEW PLAYER WAS ADDED :
MEAN (X) = 22
Let age of new player = y
Sum of Ages = 19 + 19 +20 + 20 + 20 + 21 + 22 + 22 + 22 + 22 + 23 + y
Number of players = 11 + 1 = 12
Mean(x) = sum of ages / number of players
New mean (x) = 22
x = (230 + y) / 12
22 = (230 + y) / 12
Cross multiply
264 = 230 + y
y = 264 - 230
y = 34 years
Noah is buying a pair of jeans and using a coupon for 10% off.
The total price is $56.70, which includes $2.70 in sales tax.
Noah's purchase can be modeled by the equation:
`x-0.1x+2.70=56.70`
What does the solution to the equation mean in this situation?
Answers
Answer: The answer to this equation is 53.91
Can someone pleaseeee help and if you’re correct I’ll give u brainlist! Yes or no?

Answers
Answer:
yes
Step-by-step explanation:
How many people know 2 3/2 times 4,000?
Answers
Answer:
14000
Step-by-step explanation:
2 x 4000= 8000 3/2 = 1 1/2, 1 x 4000= 4000, 8000+4000=12000,
1/2 x 4000 = 2000, 2000+ 12000= 14000
In the Diagram segment ad bisects angle bac

Answers
Since segment AD bisects angle BAC, the value of x is equal to 14.6.
What is an angle bisector?In Mathematics, an angle bisector can be defined as a type of line, ray, or segment, that bisects or divides a line segment exactly into two (2) equal angles.
By applying the angle bisector theorem to this triangle (ΔABC), we have:
AB/BD = AC/DC
19/x = 17/(20 - x)
17x = 19(20 - x)
17x = 380 - 19x
19x + 17x = 380
26x = 380
x = 380/26
x = 14.6.
In conclusion, we can reasonably infer and logically deduce that the value of x in triangle ABC is 14.6.
Read more on angle bisector here: brainly.com/question/18714022
#SPJ1
suppose babies born in a large hospital have a mean weight of 4022 grams, and a standard deviation of 266 grams. if 53 babies are sampled at random from the hospital, what is the probability that the mean weight of the sample babies would be less than 4068 grams? round your answer to four decimal places.
Answers
The probability that the mean weight of the sample babies would be less than 4068 grams is 0.8666.
We have mean weight as 4022grams,and standard deviation as 266 grams.
We need to check mean weight of the sample will be less than 4068 grams.
It means that on left side mean range is=4022-4068=-46,and
right side mean range =4022+4068=8090
So, we need to find the probability if mean range varies in between from -46 to 8090.
So, we use z-score table to find the z-score for -46 and 8090,we get
We use Z-formula which is given by
Z = (X-μ)/SE
where X is the standard mean.
Using the Z-score table, we get
Z = 0.16917 and -0.161917
Using z-score table, we get that P(0.16917)=0.4333.
Since, both of the probability occupies same space area, due to that total probability =0.4333×2=0.8666
Hence, the probability will be 0.8666.
To know more about probability, visit here:
https://brainly.com/question/11234923
#SPJ4
Follow this link to view Juan's work. Critique Juan's work by justifying correct solutions and by explaining any errors he made. For any errors made, provide and explain a correct response. Be sure to explain each key aspect of the graph.
and y’all please no bitly answers. i’ve been looking everywhere for an answer so please if you answer give the correct answer. :)

Answers
Answer:
Explain more
Step-by-step explanation:
Go to Wyzant for expert
consider the relation on 2z (i.e., the is-a-subset-of relation defined on all sets of integers).which of the properties in definition 14.7 does have?
Answers
In the relation on 2Z (i.e., the is-a-subset-of relation defined on all sets of integers), the reflexive property in definition 14.7 is the only property that is possessed by the relation.
A relation is a connection or association between two or more things. In mathematics, it is a set of ordered pairs, for example (a, b), where a belongs to a set A and b belongs to a set B. It can also be interpreted as a function with a domain and a codomain.
The reflexive property in definition 14.The reflexive property in definition 14.7 states that for all a ε A, (a, a) ε R. The set R is known to be reflexive if and only if every element of the set is related to itself.
In simpler terms, a relation is reflexive if every element in the set is related to itself. In the relation on 2Z, the only property that is possessed by the relation is the reflexive property in definition 14.7.
Therefore, it can be concluded that the relation on 2Z is a reflexive relation.
To know more about relation refer here:
https://brainly.com/question/6241820
#SPJ11
the mean of five positive integers is 1.5 times their median. four of the integers are 8, 18, 36 and 62, and the largest integer is not 62. what is the largest integer?
Answers
The largest number of the five positive integers is 146.
Mean:
The mean is the mathematical average of a set of two or more numbers. The arithmetic mean and the geometric mean are two types of mean that can be calculated. The formula for calculating the arithmetic mean is to add up the numbers in a set and divide by the total quantity of numbers in the set.
Median:
The median is the middle value in a set of data. First, organize and order the data from smallest to largest. To find the midpoint value, divide the number of observations by two. If there are an odd number of observations, round that number up, and the value in that position is the median.
Here we have to find the largest integer.
Data given:
Four of the five integers are 8, 18, 36, and 62.
It is given that mean of five numbers 1.5 times their median.
mean = (8+18+36+62 + x)/5
median = 36
mean = 1.5 × median
(124 + x) / 5 = 1.5 × 36
124 + x = 5 × 54
x = 270 - 124
= 146
Therefore we get the largest number as 146.
To know more about the mean, median and mode refer to the link given below:
https://brainly.com/question/14532771
#SPJ4
help plz if u tell ill give u 5 stars and a like plz hurry plz

Answers
-4x-y=2
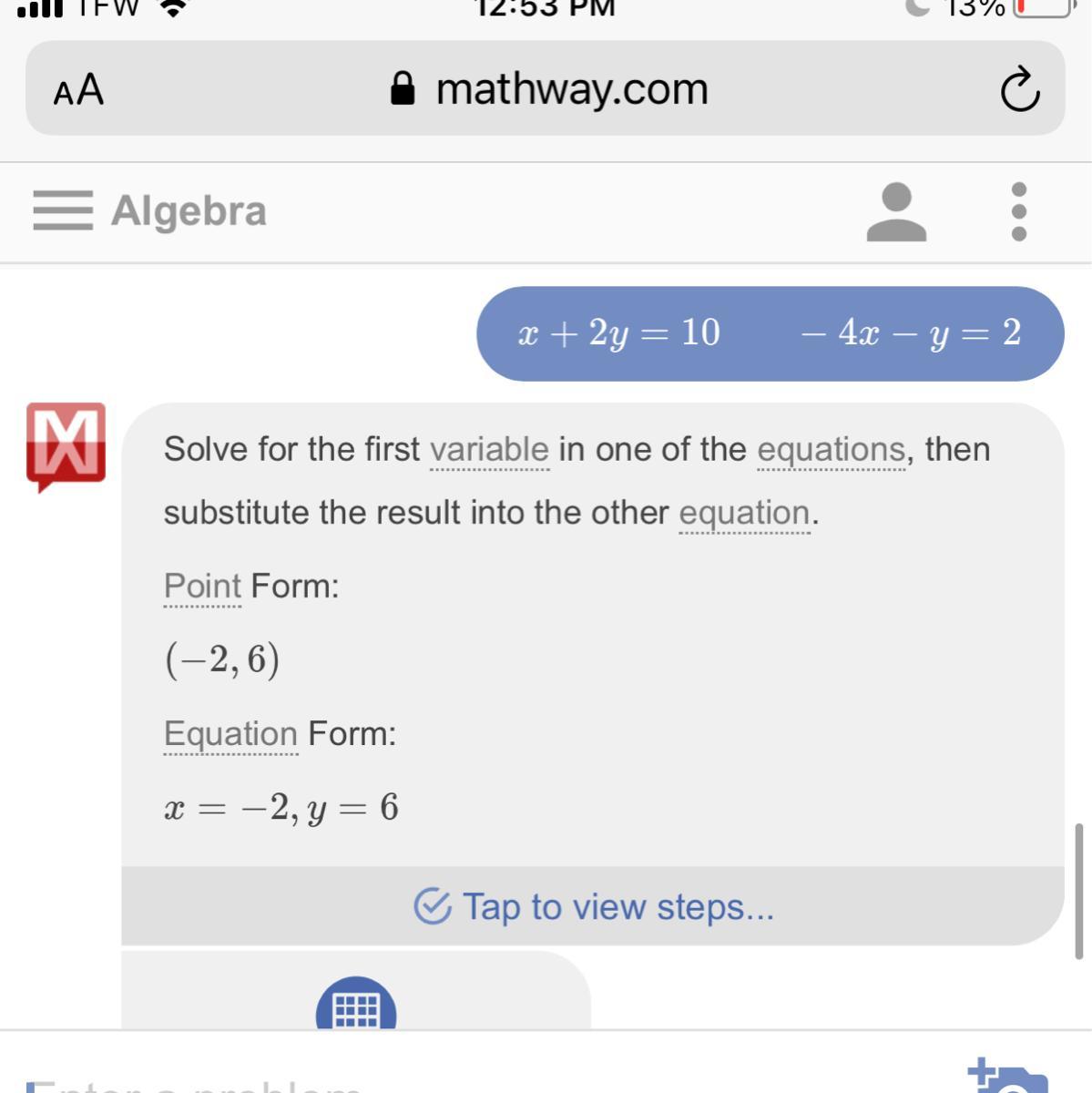
Identify the value of y.
The figure shows a right triangle. One leg has a length of 9 units. The other leg has a length of y units. The hypotenuse has a length of y plus 3 units.
y = 6
y = 12
y = 3
y = 15
Answers
Answer:
Y=12
Step-by-step explanation:
ya bae
a groundskeeper wants to reseed a soccer field that has a length of 9x+3 feet and a width of x-2 feet. which of the following equations would solve this? a) (9x+3)(x-2) b) (9x+3)+(x-2) c) (9x+3)-(x-2) d) none
Answers
I think when they said reseed the soccer field they probably meant that they want you to find the area
Can someone please help me with this two please

Answers
Answer:
1. B
2. C
Step-by-step explanation:
1. In this, we already know one side and one angle are congruent. For the triangles to be congruent by SAS, another side is necessary. Thus CB = FE
2. Here, we see that one set of sides are congruent. We see another set of angles are congruent as well. We also know that the center angle is congruent as the angles are formed by two straight lines intersecting. Since we see 2 next door angles and the side beside it congruent, they are proven congruent by AAS.
If a math test has 20 multiple choice problems, 10 fill in the blank and 5 word problems, what fraction of the problems on the test will be word problems?
Answers
Answer:
1/7
Step-by-step explanation:
what you're trying to find: # of word problems/ # of total problems
# of word problems = 5
# of total problems = 5 + 10 + 20 = 35
5/35 = 1/7
the price of fuel may increase due to demand and decrease due to overproduction. marco is studying the change in the price of two types of fuel, A and B, over time.
the price f(x), in dollars, of fuel A after x months is represented by the function below:
f(x) = 2.27(0.88)^x
part A: is the price of fuel A increasing or decreasing and by what percentage per month? justify your answer
part B: the table below shows the price g(m), in dollars, of fuel B after m months:
m (number of months): 1 | 2 | 3 | 4
g(m) (price in numbers): 3.44 | 3.30 | 3.17 | 3.04
which type of fuel recorded a greater percentage change in price over the previous months? justify your answer
Answers
a) The price of fuel A is decreasing by a percentage of 12% per month.
b) The greater percentage decay is of type A fuel.
How to model an exponential function?The standard definition of an exponential function is given as follows:
y = ab^x.
In which the parameters are given as follows:
a is the initial value.b is the rate of change.For a decaying exponential function, we have that:
b = 1 - r, |b| < 1.
In which r is the decay rate.
For fuel type A, the decay rate is given as follows:
1 - r = 0.88
r = 0.12.
For fuel type B, the parameter b is given as follows:
b = 3.30/3.44
b = 0.96.
Hence the decay rate is of:
1 - r = 0.96
r = 0.04.
(which is a lower decay rate than the 0.12 of fuel type A).
More can be learned about exponential functions at https://brainly.com/question/25537936
#SPJ1
Write an equation for the line parallel to the given line that
contains C.
C(4,6); y= -4x+1
The equation of the parallel line is
Answers
The equation of the line parallel to the given line is y + 4x = 22
The given line is y= -4x+1
Slope of the line = -4
Slope of the parallel line= -4
Equation of the line parallel to the given line which passes through C(6,4)
y - 6 = - 4 ( x - 4 )
y - 6 = -4x + 16
y + 4x = 22
Hence the equation of the parallel line is y + 4x = 22
One that stretches on all sides and has no width is referred to in geometry as a line. A straight line is, to put it simply, a line without bends. An non-curved line that extends to infinity on both sides is said to be straight.
The general equation for a straight line is y = mx + c, where m stands for the line's slope and c for its y-intercept. The most frequently used straight line equation is one that has to do with geometry.
The equation of a straight line can be written in a number of different ways, such as point-slope form, slope-intercept form, general form, standard form, etc.
To learn more about equation visit:
https://brainly.com/question/14200719
#SPJ9
Let R be the region in the fourth quadrant enclosed by the x-axisand the curve Y = X^2 - 2KX, where k > 0. if the area of the region R is 36, thenthe value of k is
(A) 2
(B) 3
(C) 4
(D) 6
(E) 9
Answers
We want to find the value of k given that the area of the region R is 36. To do this, we need to find the limits of integration and set up the integral for finding the area of the region R. The answer is (B) 3.
Since R is in the fourth quadrant and is enclosed by the x-axis and the curve Y = X^2 - 2KX, we can find the limits of integration by setting Y = 0 and solving for X:
0 = X^2 - 2KX
X(X - 2K) = 0
X = 0 or X = 2K
So the limits of integration are from X = 0 to X = 2K.
Now we can set up the integral for finding the area of the region R:
∫[0,2K] (X^2 - 2KX) dX
Integrating this expression gives:
[(1/3)X^3 - KX^2] evaluated at 0 and 2K
Plugging in the limits of integration and simplifying, we get:
(8/3)K^3 - 4K^3
Simplifying this expression, we get:
(2/3)K^3 = 36
Solving for K, we get:
K^3 = 54
Taking the cube root of both sides, we get:
K = 3
Therefore, the answer is (B) 3.
To find the value of k, follow these steps:
1. Determine the x-intercepts of the curve Y = X^2 - 2KX by setting Y = 0.
0 = X^2 - 2KX
X(X - 2K) = 0
The x-intercepts are X = 0 and X = 2K.
2. As we are looking for the area in the fourth quadrant, the integral bounds are from 0 to 2K.
3. Set up the integral for the area:
Area = ∫(X^2 - 2KX) dx, from 0 to 2K
4. Evaluate the integral:
Area = (X^3/3 - KX^2) | from 0 to 2K
= [(8K^3/3 - 4K^3) - (0)]
= 8K^3/3 - 4K^3
= (4K^3/3)
5. Set the area equal to 36 and solve for k:
36 = (4K^3/3)
9 = K^3
k = 3^(1/3) ≈ 2.08
The closest value from the given options is (A) 2.
Learn more about integration at: brainly.com/question/18125359
#SPJ11
If 2 sides of a triangle are 4 and 6 inches long the third side of a the triangle could measure
Answers
Answer:
Between 2.1 cm and 9.9 cm
Step-by-step explanation:
The third side should be more than the difference between the other two sides and less than the sum of the other two sides.
6 – 4 = 2 cm and 4 + 6 = 10 cm.
So the third side should be between 2.1 cm and 9.9 cm, and if only integers are considered then the third side should be anywhere between 3 cm and 9 cm.
The possible measure for the third side of the triangle is:
2 < x < 10
The third side could measure any length between 2 and 10 inches, but not including 2 or 10.
What is a triangle?A triangle is a 2-D figure with three sides and three angles.
The sum of the angles is 180 degrees.
We can have an obtuse triangle, an acute triangle, or a right triangle.
We have,
To find the range of possible lengths for the third side of the triangle, we can use the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Now,
Let's call the length of the third side x.
Then, we have:
4 + 6 > x and 4 + x > 6 and 6 + x > 4
Simplifying these inequalities, we get:
10 > x and x > -2 and x > 2
We see that,
The first inequality tells us that x must be less than the sum of the other two sides, which is 10.
The second inequality tells us that x must be greater than the difference between the other two sides, which is 2.
The third inequality tells us the same thing as the second inequality since the order of the sides doesn't matter.
Therefore,
The possible range of lengths for the third side of the triangle is:
2 < x < 10
This means,
The third side could measure any length between 2 and 10 inches, but not including 2 or 10.
Learn more about triangles here:
https://brainly.com/question/25950519
#SPJ2
The scatterplot that represents the monthly values of stock QRS has an r-
value of -0.993. Which best describes the correlation of the graph?
OA. Weak correlation
B. Strong positive correlation
C. Strong negative correlation
OD. No correlation
Answers
Answer:
C
Step-by-step explanation:
Because it's a negative, then we could assume that it is a negative correlation. And because it's closer to -1, it is a strong negative correlation.
The value -0.993 is Strong Negative correlation.
What is Coefficient Correlation?The strength and direction of two variables in a scatterplot are quantified by the correlation coefficient, or r value. It goes from one to one.
A perfect positive correlation is denoted by +1.A perfect negative correlation is denoted by -1.0 indicates a lack of associationSo, the value close to 1 is Strong positive correlation and close to -1 is Strong Negative correlation.
Thus, -0.993 close to -1 is Strong Negative correlation.
Learn more about Coefficient Correlation here:
https://brainly.com/question/15010561
#SPJ5
Use the conversions given below to change 63 kg into stones.
Give your answer rounded to 1 dp.
1 kg = 2.2 pounds
1 stone = 14 pounds
Answers
Answer:
63kg x 2.2 = 138.6 pounds
138.6 pounds/14 = 9.9 stones
Step-by-step explanation:
Answer:
63kg×2.2=138.6 pounds
138.6 pounds/14=9.9
gof)(6)
A. Find f(6)
B. substitute the value of g(x) into the function f(x) in place of x to find the value of f(g(x))
Answers
The value of the composite function (g o f)(6) is 3
How to evaluate the composite functionFrom the question, we have the following parameters that can be used in our computation:
f(x) = 2x + 3
g(x) = 1/5x
A. Find f(6)
substitute the known values in the above equation, so, we have the following representation
f(6) = 2 * 6 + 3
So, we have
f(6) = 15
For the function (gof)(6), we have
g(x) = 1/5x
This gives
(g o f)(6) = 1/5 * 15
Evaluate
(g o f)(6) = 3
Hence, the composite function has a solution of 3
Read more about composite function at
https://brainly.com/question/10687170
#SPJ1
Complete question
Given that f(x) = 2x + 3 and g(x) = 1/5x
Compute (gof)(6)
A. Find f(6)
B. substitute the value of g(x) into the function f(x) in place of x
Someone pls i need to fill the table under the graph

Answers
Answer:
9
11
15
Step-by-step explanation:
Read the points in the graph that correspond to y = 0, y = 2, y = 6.
Answer:
9
11
15
(Please help, problem is in the photo.)

Answers
which is y1-y2/x1-x2
(-1,3) and (5,-2)
so it becomes 3-(-2)/-1-5
m=-5/6
when two lines are perpendicular their gradients multiply to make -1
that means the gradient of L has to be 6/5
we can substitute the point on L (5,-2) and the gradient of 6/5 into y=mx+c
-2 = (6/5) x 5 + c
c = -8
the equation of line L is y= 6x/5 -8
Answer:
\(\sf y = \dfrac{6}{5} x-8\)
explanation:
coordinates: (-1, 3), (5, -2)
slope:
\(\sf \dfrac{y-y1}{x-x1}\)
\(\hookrightarrow \ \sf \dfrac{-2-3}{5--1}\)
\(\hookrightarrow \ \sf \dfrac{-5}{6}\)
The line L is perpendicular to this slope. so the slope will be:
\(\sf -(m)^{-1}\)
\(\hookrightarrow \ \sf -(\dfrac{-5}{6})^{-1}\)
\(\hookrightarrow \ \ \sf \dfrac{6}{5}\)
make equation using:
\(\sf y - y1 = m(x-x1)\)
\(\hookrightarrow \ \sf y - -2 = \dfrac{6}{5} (x-5)\)
\(\hookrightarrow \ \sf y +2 = \dfrac{6}{5} x-6\)
\(\hookrightarrow \ \sf y = \dfrac{6}{5} x-6-2\)
\(\hookrightarrow \sf y = \dfrac{6}{5} x-8\)