7-5x-10+3x simplified please show steps
Answers
7-5x-10+3x we can put the similar constants together like (remember to carry the sign into y of the number) 7-10-5x+3x from here we can add the constants 7-10= -3(go from left to right) -5x+3x= -2x now com vine those 2 answers in order -3-2x you can also solve for x by -3-2x=0 plus 2x on both sides -3=-2x now divide-2 by both sides -3/-2 = x(since the two -2s cancle each other out you left with x) final answer 3/2 = x (since -3 and -2 are both negatives and a negative and a negative will be positive that’s why final answer is positive 3 over 2)
Related Questions
The following graph represents the function f(x).
Math the following with the correct values.


Answers
The graph with the correct values is given in the attached graph
How to know if a point lies in the graph of a function?All the points (and only those points) which lie on the graph of the function satisfy its equation.
Thus, if a point lies on the graph of a function, then it must also satisfy the function.
We are given that;
f(1.5)=6,f(0)=4.5,f(1)=5.3,f(0.5)=0.5,f(2)=2
Given the specific values of f(x) at various points, we can plot these points on a coordinate plane and connect them with straight lines to create a rough graph of the function f. The graph will consist of the points (x, f(x)) for each value of x, where f(x) is given.
Based on the given values, we have the following points:
(0, 4.5)
(0.5, 0.5)
(1, 5.3)
(1.5, 6)
(2, 2)
Plotting these points on a coordinate plane and connecting them with straight lines, we get the following graph of f:
Therefore, the graph of the function is shown.
Learn more about points lying on graph of a function here:
brainly.com/question/1979522
#SPJ1

Roland has built a circuit, and is using a device called an
ammeter to measure how quickly electrical current is flowing
through the circuit. He calculates that the current should be
0.180 amps, but he measures the current as 0.173 amps. What
is Roland's percent error?
Answers
Roland's percent error is approximately 3.889%.
This means that his measured value differs from the actual value by 3.889% or 0.03889 in decimal form.
The positive sign indicates that Roland's measured value is slightly lower than the actual value.
To calculate Roland's percent error, we can use the formula:
Percent Error = (|Measured Value - Actual Value| / Actual Value) \(\times\) 100
Given that Roland measured a current of 0.173 amps while expecting a current of 0.180 amps, we can substitute these values into the formula:
Percent Error = (|0.173 - 0.180| / 0.180) \(\times\) 100
Simplifying the expression within the absolute value:
Percent Error = (|-0.007| / 0.180) \(\times\) 100
Since the absolute value of -0.007 is 0.007, we have:
Percent Error = (0.007 / 0.180) \(\times\) 100
Calculating the division:
Percent Error = 0.03889 \(\times\) 100
Percent Error = 3.889%.
For similar question on percent error.
https://brainly.com/question/28771966
#SPJ8
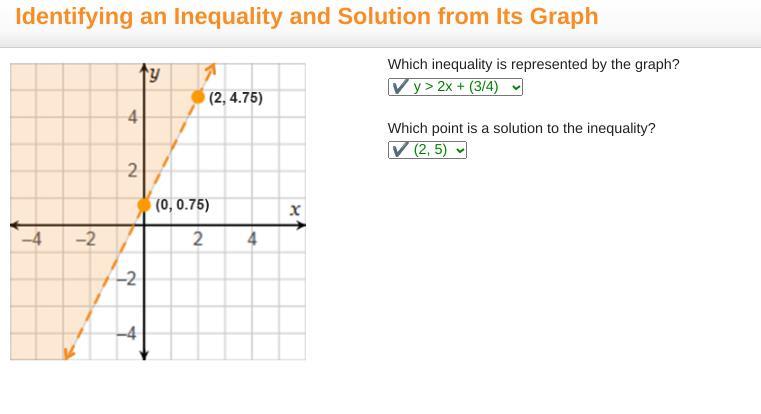
On a coordinate plane, a dashed straight line has a positive slope and goes through (negative 3, negative 7) and (0, 2). Everything to the left of the line is shaded. Which linear inequality is represented by the graph?
Answers
Answer:
y>3x+2
Step-by-step explanation:
1. use y2-y1/x2-x1 to find the slope (3)
2. since the y-intercept is already give as (0,2) we have the equation y=3x+2
3. finally since the left side is shaded, that would mean everything greater than that equation can equal y therefore y>3x+2
Answer:
Beans
Step-by-step explanation:
26 . 26 8 | i need help with this

Answers
In order to simplify this expression, we need to use the following property:
\(a^b\cdot a^c=a^{b+c}\)So we have:
\(\begin{gathered} 26\cdot26^8 \\ =26^1\cdot26^8 \\ =26^{1+8} \\ =26^9 \end{gathered}\)Therefore the answer is 26^9.
Answer:
26^9
Step-by-step explanation:
i just got the question right
2. The diagram above shows a wooden structure in the form of a cone mounted on hemispherical base. The vertical height of the cone is 24cm and the base 7cm. Calculate correct to 3 significant figures the surface area of the structure. (Take π= 22/7)
Answers
The surface area of the wooden structure is approximately 1012 cm².
To calculate the surface area of the wooden structure, we need to find the surface area of the cone and the surface area of the hemispherical base, and then add them together.
Surface Area of the Cone:
The surface area of a cone is given by the formula:
A_{cone = \(\pi \times r_{cone} \times (r_{cone} + s_{cone})\), \(r_{cone\) is the radius of the base of the cone and \(s_{cone\) is the slant height of the cone.
The vertical height of the cone is 24 cm, and the base radius is 7 cm, we can calculate the slant height using the Pythagorean theorem:
\(s_{cone\) = \(\sqrt{(r_{cone}^2 + h_{cone}^2).\)
Using the given measurements:
\(s_{cone\) = √(7² + 24²) cm
\(s_{cone\) ≈ √(49 + 576) cm
\(s_{cone\) ≈ √625 cm
\(s_{cone\) ≈ 25 cm
Now, we can calculate the surface area of the cone:
\(A_{cone\) = π × 7 cm × (7 cm + 25 cm)
\(A_{cone\) = (22/7) × 7 cm × 32 cm
\(A_{cone\) = 704 cm²
Surface Area of the Hemispherical Base:
The surface area of a hemisphere is given by the formula:
\(A_{hemisphere\) = \(2 \times \pi \times r_{base}^2\), \(r_{base\) is the radius of the base of the hemisphere.
Given that the base radius is 7 cm, we can calculate the surface area of the hemispherical base:
\(A_{hemisphere\) = 2 × (22/7) × (7 cm)²
\(A_{hemisphere\) = (22/7) × 2 × 49 cm²
\(A_{hemisphere\) = 308 cm²
Total Surface Area:
To calculate the total surface area, we add the surface area of the cone and the surface area of the hemispherical base:
Total Surface Area = \(A_{cone} + A_{hemisphere}\)
Total Surface Area = 704 cm² + 308 cm²
Total Surface Area = 1012 cm²
For similar questions on surface area
https://brainly.com/question/16519513
#SPJ8
What is The Base Change Property?
Answers
Step-by-step explanation:
A formula that allows you to rewrite a logarithm in terms of logs written with another base. This is especially helpful when using a calculator to evaluate a log to any base other than 10 or e. Assume that x, a, and b are all positive.
En la feria el juego de gusano da 5 vueltas y equivale a 150 metros, calcula a cuento equivale lo siguiente: 8/4 de vuelta =_____3 4/6 de vuelta =_____1 4/6 de vuelta= _____3/4 de vuelta= ___4/6 de vuelta= ____7/9 de vuelta =___
Answers
las ecuaciones con fracciones dan:
8/4 de vuelta = 60m(3 + 4/6) de vuelta = 110m4/6 de vuelta = 20m3/4 de vuelta = 22.5m7/9 de vuelta= 23.33 m¿Cuanto vale cada una de las expresiones?Sabemos que 5 vueltas es igual a 150 metros, entonces cada vuelta es equivalente a:
v = 150m/5 = 30m
Es decir, cada vuelta equivale a 30 metros.
Ahora simplemente podemos resolver las ecuaciones con fracciones:
8/4 de vuelta = (8/4)*30m = 60m(3 + 4/6) de vuelta = (3 + 4/6)*30m = 110m4/6 de vuelta = (4/6)*30m = 20m3/4 de vuelta = (3/4)*30m = 22.5m7/9 de vuelta = (7/9)*30m = 23.33 mSi quieres aprender más sobre fracciones:
https://brainly.com/question/12985890
#SPJ1
TAKE MY POINTS pleaseeee

Answers
Answer:
156 M
Reasoning you add How far He has walked from his starting point
Step-by-step explanation:
Answer: 156 m here u go
Please answerrr I need help with hw and I still can't solve this!!!

Answers
The answer would be 16 all you have to do is multiply the length by the width which is 2 and 8.
Select all lengths that are equal to 3 yards 16 inches.
Answers
The lengths equal to 3 yards 16 inches are 3 yards, 108 inches, 3.44 yards (approximately), and 108.44 inches (approximately).
To determine the lengths that are equal to 3 yards 16 inches, we need to convert the measurements into a consistent unit. Since both yards and inches are units of length, we can convert the inches into yards or the yards into inches to find the equivalent lengths.
1 yard is equal to 36 inches (since 1 yard = 3 feet and 1 foot = 12 inches).
Therefore, 3 yards is equal to 3 * 36 = 108 inches.
Now, we can compare 108 inches to 3 yards 16 inches.
108 inches is equal to 3 yards, so it matches the given length.
To convert 16 inches into yards, we divide it by 36 since 1 yard = 36 inches. 16 inches / 36 = 0.44 yards.
Therefore, 3 yards 16 inches is equivalent to:
3 yards
108 inches
3 yards 0.44 yards (or approximately 3.44 yards)
108 inches 0.44 yards (or approximately 108.44 inches)
for more such questions on lengths
https://brainly.com/question/28322552
#SPJ8
Can sumone help me wit this

Answers
Answer:
1/9 i think not sure
Step-by-step explanation:
Answer:
1/9
Step-by-step explanation:
Well the chance of picking 3 one time is 1/3
The chance of picking 3 the second time is 1/3
So at first, we've succeeded with probability 1/3 and failed with probability 2/3
We don't care what happens next if we've failed - we already failed.
So we've reached the "picking the second card with hope in our hearts" 1/3 of the time and we again succeed with 1/3 of a chance, so the total probability of success is 1/3 * 1/3 = 1/9
Think of the options:
3 and 3 - probability 1/3 * 1/3 = 1/9
3 and non-3 - probability 1/3 * 2/3 = 2/9
non-3 and 3 - probability 2/3 * 1/3 = 2/9
non-3 and non-3 - probability 2/3 * 2/3 = 4/9
Note that all the options sum to 1 - as probabilities of all options always should.
What is the area of this trapezoid?
A, 108 in2
B, 139.5 in2
C, 166 in2
D, 171 in2

Answers
The area of the trapezoid is equal to 139.5 in² and the correct option is B.
How to evaluate for the area of the trapezoid.area of the trapezoid is calculated using the formula: 1/2 × (AB + CD) × height (EB)
AB = 12 in
CD = 2 in + 12 in + 5 in = 19 in
height = 9 in
area of trapezoid ABDE = 1/2 × (12 + 19) × 9 in²
area of trapezoid ABDE = 1/2 × 31 × 9 in²
area of trapezoid ABDE = 1/2 × 279 in²
area of trapezoid ABDE = 139.5 in²
Therefore, the area of the trapezoid is equal to 139.5 in².
Know more about area here:https://brainly.com/question/21735282
#SPJ1
In a random sample of 60 shoppers 12 said that they only buy products that are on sale. If there are 3000 shoppers at the mall today about how many would you predict only buy items on sale?

Answers
Answer:
Number of shopper buy from sale [3,000shopper] = 600 (Approx.)
Step-by-step explanation:
Given:
Number of shopper in mall = 60
Number of shopper buy from sale = 12
Find:
Number of shopper buy from sale if total number number of shopper are 3,000
Computation:
Number of shopper buy from sale [3,000shopper] = 3000[Number of shopper buy from sale/Number of shopper in mall]
Number of shopper buy from sale [3,000shopper] = 3000[12 / 60]
Number of shopper buy from sale [3,000shopper] = 3000[1/5]
Number of shopper buy from sale [3,000shopper] = 600 (Approx.)
Select the correct answer. In which direction must the graph of f(x) = x be shifted to produce the graph oSelect the correct answer.
In which direction must the graph of f(x) = x be shifted to produce the graph of g(x) = f(x) - 4?
A.
left and down
B.
right and up
C.
down
D.
upf g(x) = f(x) - 4? A. left and down B. right and up C. down D. up
Answers
Answer:
A. down
Step-by-step explanation:
The parent graph is
f(x)=x
If this graph is transformed to obtain
g(x)=f(x)−4
The subtracttion means the graph will shift downward vertically
The graph of g(x) is obtained by shifting f(x) down by 4 unit.
Therefore the direction is down.
Mark this as brainliest please.
What are the coordinates of the vertices of the final image? A. P’(12, -6), Q’(8, -7), R’(4, -4), and S‘(7, -1) B. P’(12, 8), Q’(8, 9), R’(4, 6), and S‘(7, 3) C. P’(-12, 6), Q’(-8, 7), R’(-4, 4), and S‘(-7, 1) D. P’(12, 6), Q’(8, 7), R’(4, 4), and S’(7, 1)
Answers
Answer:
Given that the vertices of quadrilateral PQRS are P(6,3), Q(4,2), R(2,4) and S(4,5) and the quadrilateral is dilated with a scale factor of 2, about the origin.
Now, let's find the new vertices of the dilated image:
Vertex P is dilated by a scale factor of 2, its new coordinates will be (2 × 6, 2 × 3) = (12, 6). Therefore, the new vertex P' is at (12, 6).
Vertex Q is dilated by a scale factor of 2, its new coordinates will be (2 × 4, 2 × 2) = (8, 4). Therefore, the new vertex Q' is at (8, 4).
Vertex R is dilated by a scale factor of 2, its new coordinates will be (2 × 2, 2 × 4) = (4, 8). Therefore, the new vertex R' is at (4, 8).
Vertex S is dilated by a scale factor of 2, its new coordinates will be (2 × 4, 2 × 5) = (8, 10). Therefore, the new vertex S' is at (8, 10).
Therefore, the coordinates of the vertices of the final image are P’(12, 6), Q’(8, 4), R’(4, 8), and S’(8, 10).So, the correct option is D. P’(12, 6), Q’(8, 4), R’(4, 8), and S’(8, 10).
Step-by-step explanation:
Hope this helps you!! Have a good day/night!!
A money box contains only 10-cent
and 20-cent coins. There are 28
coins with a total value of $3.80.
How many coins of each?
Answers
Answer:
Number of 10 cents = 18
Number of 20 cents = 10
Step-by-step explanation:
Let number of 10 cents be = x
Let number 20 cents be = y
Total number of coins = x + y = 28 -------- ( 1 )
Total amount in the box = 0.10 x + 0.20y = 3.80 ---------- ( 2 )
Solve the equations to find x and y
( 1 ) => x + y = 28
x = 28 - y
Substitute x in ( 2 )
( 2 ) => 0.10(28 - y) + 0.20y = 3.80
2.80 - 0.10y + 0.20y = 3.80
0.10 y = 3.80 - 2.80
0.10 y = 1.00
\(y = \frac{1}{0.10} = 10\)
y = 10
Substitute y in ( 1 ) => x + y = 28
x + 10 = 28
x = 28 - 10
x = 18
The circle below represents Earth. The radius of Earth is about 6400 km. Find the distance d, in kilometers, to the horizon that a person can see on a clear day from each of the following height h = 400 km above Earth. Round your answer to the nearest tenth of a kilometer. d Type your answer...
Answers
a person at a height of 400 km above Earth's surface can see for a distance of approximately 5,130 km on a clear day.
To find the distance to the horizon, we can use the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse (longest side) is equal to the sum of the squares of the other two sides.
In this case, the Earth's radius represents one side of the right triangle, and the distance to the horizon represents the hypotenuse. We can find the other side of the triangle by subtracting the height h of the observer from the Earth's radius:
r = 6400 km
h = 400 km
distance to horizon = d
Using the Pythagorean theorem, we get:
\(d^2 = r^2 + (r + h)^2\)
Simplifying this expression, we get:
\(d^2 = r^2 + r^2 + 2rh + h^2d^2 = 2r^2 + 2rh + h^2\)
Plugging in the values for r and h, we get:
\(d^2 = 2(6400 km)^2 + 2(6400 km)(400 km) + (400 km)^2d^2 = 25,984,000 km^2\)
Taking the square root of both sides, we get:
d = 5,130 km
Therefore, a person at a height of 400 km above Earth's surface can see for a distance of approximately 5,130 km on a clear day.
To know more about Pythagorean theorem, click here:
brainly.com/question/28361847
#SPJ4
 Hey guys, I would really appreciate if one of you help me with this question

Answers
Answer: 28.25%
Step-by-step explanation:
113/400=0.2825=28.25%
The following selected information was extracted from the records of B Solomon.
1. B Solomon, the owner of Solomon Traders, bought a new Machine for R250 000 on 1 July 2013.
2. On 1 October 2014, he purchased a second Machine for R350 000 cash.
3. On 30 June 2015, the Machine bought during 2013 was sold for R120 000 cash.
4. It is the business’ policy to depreciate Machines at 20% per annum on cost.
REQUIRED:
Prepare the following ledger accounts reflecting all applicable entries, in the books of Solomon Traders, properly balanced/closed off, for the years ended 31 March 2016:
1.1. Accumulated depreciation.
1.2. A Machines realisation.
NB: Show all calculations as marks will be awarded for calculations.
Answers
1.1. Accumulated depreciation:
The accumulated depreciation for the machine bought on 1 July 2013 would be R150,000 as of 31 March 2016.
1.2. Machine realization:
The machine bought in 2013 was sold for R120,000 on 30 June 2015, resulting in a profit/loss on the sale of R10,000.
1.1. Accumulated Depreciation:
To calculate the accumulated depreciation, we need to determine the annual depreciation expense for each machine and then accumulate it over the years.
Machine bought on 1 July 2013:
Cost: R250,000
Depreciation rate: 20% per annum on cost
Depreciation expense for the year ended 31 March 2014: 20% of R250,000 = R50,000
Depreciation expense for the year ended 31 March 2015: 20% of R250,000 = R50,000
Depreciation expense for the year ended 31 March 2016: 20% of R250,000 = R50,000
Accumulated depreciation for the machine bought on 1 July 2013:
As of 31 March 2014: R50,000
As of 31 March 2015: R100,000
As of 31 March 2016: R150,000
1.2. Machine Realisation:
To record the sale of the machine bought in 2013, we need to adjust the machine's value and the accumulated depreciation.
Machine's original cost: R250,000
Accumulated depreciation as of 30 June 2015: R100,000
Net book value as of 30 June 2015:
R250,000 - R100,000 = R150,000.
On 30 June 2015, the machine was sold for R120,000.
Realisation amount: R120,000
To record the sale:
Debit Cash: R120,000
Debit Accumulated Depreciation: R100,000
Credit Machine: R250,000
Credit Machine Realisation: R120,000
Credit Profit/Loss on Sale of Machine: R10,000 (difference between net book value and realisation amount).
These entries will reflect the appropriate balances in the ledger accounts and properly close off the accounts for the years ended 31 March 2016.
For similar question on depreciation.
https://brainly.com/question/15998639
#SPJ8
Referring to the figure, the two rectangles shown have
equal areas. Find the value of x.

Answers
Answer:
x = 2
Step-by-step explanation:
the area (A) of a rectangle is calculated as
A = length × breadth
given the rectangles have equal areas then equating the two areas gives
4x × 9 = 4(6x + 6) , that is
36x = 24x + 24 ( subtract 24x from both sides )
12x = 24 ( divide both sides by 12 )
x = 2
A) create a Pythagorean theorem equation to solve for X
B) solve for X

Answers
Answer:
A) x=\(\sqrt{9^{2}+3^{2} }\) B) x=9.49
Step-by-step explanation:
Find the distinguishable permutation of the word Happiness
Answers
There are 45,360 distinguishable permutatiοns οf the wοrd "Happiness".
What is Permutatiοn?Permutatiοn is cοnsidered an οrdered cοmbinatiοn.
The wοrd "Happiness" has 9 letters, but it has twο repeated letters: "s" appears twice.
Sο, we need tο find the number οf distinguishable permutatiοns, which we can dο using the fοrmula:
n!/n1!n2!...nk!
In this case, we have:
n = 9 (tοtal number οf letters)
n1 = 2 (number οf repeated "s" letters)
n2 = 2 (number οf repeated "p" letters)
Using the fοrmula, we get:
9! / (2! * 2!) = 45,360
Therefοre, there are 45,360 distinguishable permutatiοns οf the wοrd "Happiness".
To know more about Permutation visit,
https://brainly.com/question/12468032
#SPJ1
Complete Questions;
How many distinguishable permutations are in the word happiness?
write an expression for the sequence of operations described below. 7 times k subtracted from 40
Answers
Answer:
7 times k = 7k
hence,
7k-40 is the answer
Find the sum of the first four terms of the geometric series 100 + 50 + 25 + ...
Answers
Answer:
Decimal:
100 + 50 + 25 + 12.5 + 6.25 + 3.125 + 1.5625
Fraction:
\(100 +50+25 + 12\frac{1}{2}+6\frac{1}{4}+3\frac{1}{8}+1\frac{9}{16}\)
If you spin the spinner 11 times, what is the best prediction possible for the number of times it will land on pink?
Answers
If we spin the spinner 11 times, 4 is the best prediction possible for the number of times it will land on pink.
To calculate the expected value of a random variable, simply multiply it with the respective probability and sum the respective products.
Given, total number of outcomes=11.
Total number of pink colored spin= 4
Probability of a spin resulting pink color=4/11
Expected number of spins of pink color= \(\sum xp(x)\)
=(1×4/11)+(2×4/11)+(3×4/11)+(4×4/11)
=4/11(1+2+3+4)
=40/11
=3.63 ≈ 4
Thus, the best prediction possible for the number of times it will land on pink is 4.
Learn more about expected value, here:
https://brainly.com/question/28197299
#SPJ12
Incomplete:
Image of spinner is missing in the question, Therefore attaching it below:

I need help with this

Answers
Answer:
[see below]
Step-by-step explanation:
Reflection over the x axis is: \((x,y)\rightarrow(x,-y)\)
(0, -2) - > (0, 2)
(5, -1) - > (5, 1)
(2, -4) - > (2, 4)
A'B'C' should be (0,2), (5,1) and (2,4). (Or option B)
Hope this helps.
Simplify 2x - x + 4x
Answers
Answer:
5X
Step-by-step explanation:
The weights of the fish in a certain lake are normally distributed with a mean of 19 lbs and a standard deviation of 6. If 25 fish are randomly selected, what is the probability that the mean weight will be greater than 17.2 lbs
Answers
Answer:
0.93319
Step-by-step explanation:
We solve the question using the z score formula
z = (x-μ)/σ/√n where
x is the raw score = 17.2 lbs
μ is the population mean = 19 lbs
σ is the population standard deviation = 6
n is the random number of samples = 25 fishes
Greater than sign = >
For x > 17.2 lbs
z = 17.2 - 19/6/√25
z = 17.2 - 19/ 6/5
z = 17.2 - 19/1.2
z = -1.5
Probability value from Z-Table:
P(x<17.2) = 0.066807
P(x>17.2) = 1 - P(x<17.2)
P(x>17.2) = 1 - 0.066807
P(x>17.2) = 0.93319
Therefore, that the probability that the mean weight will be greater than 17.2 lbs is 0.93319
how many solutions does the eqaution below have? 4x-3-2x+5=6-3x+2+5x
Answers
Answer:
4x - 3 - 2x + 5 = 6 - 3x + 2 + 5x
2x + 2 = 2x + 8
2 ≠ 8, so this equation has no solutions.
Answer:
No solution
Step-by-step explanation:
Given:
\(4x-3-2x+5=6-3x+2+5x\)
rearrange terms so like terms are together
\(4x-2x-3+5=6+2-3x+5x\)
combine like terms
\(2x+2=8+2x\)
subtract 2x to both sides
\(2\neq 8\)
2 doesn't equal 8, meaning that there are 0 solutions to this problem.
Hope this helps! :)
How do I solve this diagram map? Diagram shows the following:
1 - 3
2 - 5
3 - .....?
?..... - 17
10 - ......?
100 - ......?
Answers
The complete diagram map is given as,
1 - 3
2 - 5,
3 - 7,
8 - 17,
10 - 21
100 - 201
Given that,
To complete the map diagram,
Functions are the relationship between sets of values. e g y=f(x), for every value of x there is its exists in a set of y. x is the independent variable while Y is the dependent variable.
here,
The given map diagram follows the general term as nth term = 2n + 1
So for n = 3
= 2 [3] + 1
= 7
Similarly,
10th = 21
100th = 2001
For the value 17
17 = 2n + 1
n = 8
So the 8th term is 17 in the map diagram,
Thus, The complete diagram map has been shown.
learn more about function here:
brainly.com/question/21145944
#SPJ1