9. A ship sails 20km due North. It changes
direction and then sails 15km due East.
How far is it from its starting point?
Answers
Answer:
Ans = appx 10.439 units
Step-by-step explanation:
This answer will vary depending on the starting latitude of the ship due to earth not being flat, despite suddenly popular opinions.
So if we used a flat cartesian space ignoring the curvature of the earth we could have a fixed constant answer to this question. Lets do it that way.
Just to clarify: NO the earth is not flat.
Another assumption of this question is the difference between compass north and true north, which we have to throw out for the same reasons.
Real world answers to this question would not be as simple… #imjustsaying
Ok so first travel northeast, lets call that a bearing of 45 degrees directly northeast to also squash any variations there… then a bearing of 250 degrees which ill assume is not a relative bearing (LOTS OF ASSUMPTIONS GOING ON HERE) which is sortof in the west-southwest direction.
The angle at the turn goes from 45 to 250. reversing the 45 shows our angle to be between 250 and 180+45=225 so the angle is 25 degrees with one leg being 20 units (kilometers) long and the other leg being 12 units long. How many units apart are the two points that are connected to that angle?
(12sin(25))^2+(20–12cos(25))^2 = x^2
Enjoy calculating. Make sure that 25 is in degrees and not in radians.
Ans = appx 10.439 units
Related Questions
Last year, Singer A performed one more than four times as many shows during concert tours than Team B. The number of Singer A concert tour shows exceeded the number of shows by Team B by 16. How many concert shows did each perform?
Answers
Team A performed 21 shows.
Team B performed 5 shows.
A = 4B + 1
B = A - 16
Substitute 4b + 1 for a in b = a − 16:
b = a − 16
b = 4b + 1 − 16
b= 4b − 15 (Simplify both sides of the equation)
b − 4b = 4b − 15 − 4b (Subtract 4b from both sides)
−3b = −15
−3b/−3 = −15/−3(Divide both sides by -3)
b=5
Substitute 5 for b in a = 4b + 1:
a = 4b + 1
a = (4)(5) + 1
a = 21
An equation is formed of two equal expressions. The number of concerts performed by A and B is 21 and 5, respectively.
What is an equation?An equation is formed when two equal expressions are equated together with the help of an equal sign '='.
Let the number of concerts performed by Singer A and Team B be represented by A and B, respectively.
Given that Singer A performed more than four times as many shows during concert tours as Team B. Therefore, we can write,
A = 4B + 1
Also, the number of Singer A concert tour shows exceeded the number of shows by Team B by 16. Therefore,
A = B + 16
As we got two equations written for A, equate the two equations equal to each other as shown.
A = A
4B + 1 = B + 16
4B - B = 16 - 1
3B = 15
B = 15/3
B = 5
Now, substitute the value of B in any one of the equations of A,
A = B + 16
A = 5 + 16
A = 21
Hence, the number of concerts performed by A and B is 21 and 5, respectively.
Learn more about Equation here:
https://brainly.com/question/14686792
#SPJ2
Which number is the largest

Answers
Step-by-step explanation:
0.153 is the largest number
Answer:
I believe 0.153 to be the greatest
Step-by-step explanation:
0.153
15%= 0.15
1/12= 0.0833333
1/7= 0.1428571429
Graham wrote the system of equations.
6x−8y=−16y=34x+8
What is true about the system of equations that Graham wrote?
A
It has no solution.
B
It has 1 solution.
C
It has 2 solutions.
D
It has infinitely many solutions.
Answers
Answer:
B
Step-by-step explanation:
6x -8y = - 16y
6x = -8y
8y = 17x + 4
-8y = -17x - 4
6x = -17x - 4
23x = -4
x = -4/23
I need help with this

Answers
Answer:
The solution for problem a is cross multiplication
5×500=2500 and 15×x=15× so 15×=2500
divide both sides by the coefficient 15. 15x ÷15=×
divide 2500 by 15=500
x=500/3= approximately 166.7
Solution for b:
This one's easy!!
10/20=x/500
cross multiply
10×500=5000
20×X=20x
now we have the equation. 20x=5000
stay with me. I hope this makes sense ^_^
divide both sides by the coefficient 20
20x÷20=x
5000÷20=250
x=250
a is true
i hope this helps ;)


please help!!! if i don’t get this test right then i fail and i really can’t ! i’ll mark brainlyist ! pleasee
anyone

Answers
Answer:
208 cubic units
Step-by-step explanation:
The composite figure in the picture is composed of a triangular prism and a rectangular prism, both which can be calculated by the base * height formula.
First, let’s calculate the volume of the triangular prism:
The base is the area of the triangle base, which is dc/2, or 4*3/2, which is 6. Next, multiply the area of the base by the height “b”: 6 * 8 = 48.
Now, let’s calculate the volume of the rectangular prism:
The base is the rectangular base’s area, which is a*c, or 5*4, which is 20. Next multiply the base by the height “b”: 20 * 8 = 160
Now, add up the volumes of the rectangular and triangular prisms:
160 + 48 = 208 cubic units
solve the following differential equation by variation of parameters. fully evaluate all integrals. find the most general solution to the associated homogeneous differential equation. use and in your answer to denote arbitrary constants, and enter them as c1 and c2. c1cos(4x) c2sin(4x) 1/16ln(cos(4x))cos(4x) 1/4xsin(4x) help (formulas) find a particular solution to the nonhomogeneous differential equation . help (formulas) find the most general solution to the original nonhomogeneous differential equation. use and in your answer to denote arbitrary constants. help (formulas)
Answers
The most general solution to the associated homogeneous differential equation is y=x/2-1/4
How will you solve this equation?C=0
dy/dx+2y=x
Use the formula:
\(\int\ \,xe^(2x)dx=e^(2x)\)((x/2−1/4).
We know that a linear differential equation is written in the standard form:
y' + a(x)y = f(x)
we get that: a(x)=2 and f(x)=x.
We know that the integrating factor is defined by the formula:
u(x)=\(e^{\int\ \, a(x) dx}\)
⇒ u(x)=\(e^{∫ 2 dx}\)= \(e^{2x}\)
The general solution of the differential equation is in the form:
y=\frac{ ∫ u(x) f(x) dx +C}{u(x)}
⇒ y=\frac{\(e^{2x}\)· x dx + 0}\({e^{2x}}\)
y=\frac{\(e^{2x}\) (x/2-1/4)\(}{e^{2x}\)
y=x/2-1/4
Hence, the most general solution to the associated homogeneous differential equation is y=x/2-1/4.
Learn more about differential equations at:
brainly.com/question/28099315
#SPJ1
A bucket contains 72 red, 48 blue, 48 green, and 48 yellow crayons. The art teacher also has 120 pieces of drawing paper. What is the largest number of identical kits the art teacher can make with all of the crayons and all of the paper?
Answers
The art teacher can make a maximum of 24 identical kits using all the crayons and drawing paper for proper distribution.
To determine the largest number of identical kits the art teacher can make using all the crayons and drawing paper, we need to find the greatest common divisor (GCD) of the quantities.
The GCD represents the largest number that can divide all the quantities without leaving a remainder.
The GCD of the quantities of crayons can be found by considering the prime factorization:
72 = 2³ × 3²
48 = 2⁴ × 3
48 = 2⁴ × 3
48 = 2⁴ × 3
The GCD of the crayons is 2³ × 3 , which is 24.
Now, we need to find the GCD of the quantity of drawing paper:
120 = 2³ × 3 × 5
The GCD of the drawing paper is also 2³ × 3 , which is 24.
Since the GCD of both the crayons and drawing paper is 24, the art teacher can make a maximum of 24 identical kits using all the crayons and drawing paper.
Each kit would contain an equal distribution of crayons and drawing paper.
Learn more about distribution here:
brainly.com/question/30034780
#SPJ1
What should you substitute for x in the second equation (bottom equation) in order to solve the system by the substitution method?

Answers
We substitute -1+1/6y for x in the second equation (bottom equation) in order to solve the system by the substitution method.
The given system of equations are 2x-1/3y = -2...(1)
3x+y=1...(2)
We solve this system of equations by using substitution method.
Let us solve for x in equation to substitute it in equation (2).
2x=-2+1/3y
Divide both sides of equation by 2.
x=-1+1/6y
Now plug in the value of x in equation 2.
Hence, we substitute -1+1/6y for x in the second equation (bottom equation) in order to solve the system by the substitution method.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Three vertices of a parallelogram are shown in the figure below.
Give the coordinates of the fourth vertex.
(-4,9)
(-6,-5)
(1.-7)

Answers
Answer:
(3, 7)
Step-by-step explanation:
Given that points (-4,9), (-6,-5), and (1.-7) are three vertices of a parallelogram with segments connecting them in order, you want the point that is the fourth vertex.
ParallelogramThe diagonals of a parallelogram bisect each other, which means they have the same midpoint:
((-4, 9) +(1, -7))/2 = ((-6, -5) +(x, y))/2
Multiplying by 2 and subtracting the point on the right side, we have ...
(-4, 9) +(1, -7) -(-6, -5) = (x, y)
(-4 +1 +6, 9 -7 +5) = (x, y) = (3, 7)
The fourth vertex is (3, 7).
__
Additional comment
In general three points can define three possible parallelograms. Here, the segments connecting the points are presumed to be the sides of the parallelogram, so reducing the number of possibilities to just one.
The fact that the diagonal midpoints are the same is useful for solving a variety of problems involving parallelograms.
Find the critical F-value for a two-tailed test using the indicated level of significance a and degrees of freedom d.f.n and d.f.p.
a = 0.01, d.f-N = 8, d.f.p = 6
The critical F-value is...(?)
(Round to two decimal places as needed.)
Answers
Explanation - d = 0.01
Dfn - 4
Dfd - 7
Using F Table -
Critical Value - 7.85

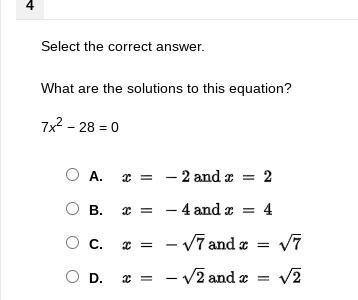
Select the correct answer. What are the solutions to this equation? 7x2 − 28 = 0A. x=-2 and x=2
B. x=-4 and x=4
C. x=the negative square root of 7 and x= the square root of 7
D. x= the negative square root of 2 and x= the square root of 2
Answers
Answer:
x = 2
x = -2
Step-by-step explanation:
Divide both sides of the equation by 7.
Moove the constant to the right and change its sign.
Simplify the equation.
Separate the solutions.
Determine a series of transformations that would map Figure J onto Figure K. J
Figure.
Figure

Answers
Figure J is rotated 90° clockwise and then translated by 3 units toward the right.
What is a transformation of a shape?A point, line, or mathematical figure can be converted in one of four ways, and each has an effect on the object's structure and/or position.
Rotation does not change the shape and size of the geometry. But changes the orientation of the geometry.
The translation does not change the shape and size of the geometry. But changes the location.
Figure J is rotated 90° clockwise and then translated by 3 units toward the right.
More about the transformation of the shape link is given below.
https://brainly.com/question/27224339
#SPJ1
Can someone one plz answer this for me !

Answers
Answer:
-7
Step-by-step explanation:
Also for the last two you gave, the answers to your questions were wrong. They gave you the wrong answer. The answer for the other 2 were A ($30) and the slope for the other answer was (1/2)
In the diagram, b || c. Find the value of y

Answers
Using the corresponding angle theorem, the value of y is 36 degree.
In the given question, b||c.
We have to find the value of y.
Given: b||c
Find: Value of y
Let x be the value of side angle of (2y+34) degree.
So, using the corresponding angle theorem
x = 74 degree
As we know that the sum of straight line is 180 degree.
So 2y+34+x = 180
Now putting the value of x
2y+34+74=180
After simplifying
2y+108=180
Subtract 108 on both side, we get
2y=72
Divide by 2 on both side, we get
y=36
Hence, the value of y is 36 degree.
To learn more about Corresponding Angle Theorem link is here
brainly.com/question/16017873
#SPJ4
A square piece of cardboard has an area of 64 square inches. How long is each side ?
Answers
Answer:
Each side is 8 in==================
Let each side is x.
The area is 64 in².
x² = 64x = √64x = 8 inStep-by-step explanation:
if the area is 64cm, each side would be 8cm
since Area of square = side by side
\(64 = {s}^{2} \\ \sqrt{64} = \sqrt{s} \\ 8 = s\)

HURRY PLEASE!!!!!
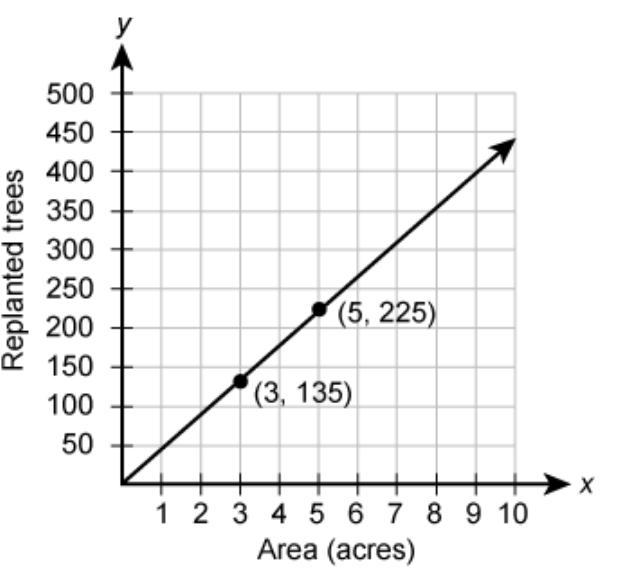
This graph shows a proportional relationship.
What is the constant of proportionality?
Answers
The constant of proportionality for the given graph is k = 45.
What is constant of proportionality?The ratio that establishes a proportionate link between any two given values is referred to as the constant of proportionality. The constant of proportionality may also be referred to by the labels constant ratio, constant rate, unit rate, constant of variation, or even rate of change.
A proportional connection is simple to graph on a coordinate plane as a straight line. Because it is directly proportional—the slope serves as the proportionality constant—it is a straight line. Because of the constant proportionate change along the x and y axes, the slope or increase is constant.
The constant of proportionality is given as:
y = kx
This equation can be written as follows:
k = y/x
Using the coordinates of point on the graph we have:
k = 225/5 and k = 135/3
k = 45
Hence, the constant of proportionality for the given graph is k = 45.
Learn more about proportionality here:
https://brainly.com/question/29126727
#SPJ1
Determine whether the
quadratic function
y=x² + 4x + 6 has
a maximum or minimum value.
Then find the value.
O maximum
minimum
The value is
Answers
Answer:
(a) The function has a minimum value
(b) The minimum value is 2
Step-by-step explanation:
(a)Currently y = x^2 + 4x + 6 is in standard form, whose general equation is
y = ax^2 + bx + c.
We know that for our function a = 1.
When a > 0, the parabola opens upward and the vertex is a minimumWhen a < 0, the parabola opens downward and the vertex is a maximumThus, y = x^2 + 4x + 6 must have a minimum value.
(b) Whenever a problem asks for the minimum value, it's asking for the y-coordinate of the minimum.
Step 1: First we can find the x-coordinate of the minimum using the equation -b/2a from the quadratic formula.
Plugging in 4 for b and 1 for a, we get:
x-coordinate of minimum = -4 / 2(1)
x-coordinate of minimum = -4 / 2
x-coordinate of minimum = -2
Step 2: Now we can plug in -2 for x in the quadratic function. The result will be our minimum value:
f(-2) = (-2)^2 + 4(-2) + 6
f(-2) = 4 - 8 + 6
f(-2) = -4 + 6
f(-2) = 2
Thus, the minimum value of the quadratic function is 2.
Can't manage to figure out this question. Can anyone help?

Answers
Answer:
Z=20
Y=16
X= 12
Step-by-step explanation:
Hope it helps
Find the value of X and Y if one angle is 46
Answers
Answer:
X
Step-by-step explanation:
A computer processes jobs on a first-come, first served basis in a time-sharing environment. The jobs have Poisson arrival rates average 0.6 jobs per minute. The objective in processing these jobs is that they spend no more than 5 minutes, on average, in the system. Assuming exponential service times, how fast does the computer have to process jobs (in minutes), on average, to meet this objective
Answers
Answer:
0.8 minutes
Step-by-step explanation:
From the given information:
The arrival time for the jobs to the computer obeys a Poisson distribution;
Thus, the arrival rate is:
\(\lambda = 0.6 \ jobs \ per \ minute\)
Assuming the average time spent on the jobs in the system is denoted by:
\(W_s= 5 \ minutes\)
The average time a job process in the system can be expressed as follows:
\(W_s = \dfrac{1}{\mu - \lambda}\)
From above formula:
\(\mu =\) service rate
\(\lambda =\) arrival rate
replacing the values;
\(5 = \dfrac{1}{\mu - 0.6}\)
\(5(\mu - 0.6) = 1\)
Open brackets
\(5 \mu - 3 = 1\)
\(5 \mu = 3+ 1 \\ \\ \mu = \dfrac{4}{5}\)
\(\mu =\) 0.8 minutes
You are planning a road trip. Total miles traveled are 1,128.3 miles. My car gets 40 miles per gallon and gas is $3.89 per gallon. how much will my gas cost?
Answers
Answer: the cost of gas for traveling 1,128.3 miles is $109.73
Step-by-step explanation:
Given:
cost per gallon of gas is $3.89
total miles traveled is 1128.3 miles
the car can travel 40 miles per gallon
gas is required to travel 1128.3 miles= total miles traveled / miles traveled
per gallon
=1128.3/40 gallon
= 28.2075-gallons
we know that the cost per gallon of gas is $3.89
from this, we can find the cost for 28.2075-gallon
the cost for 28.2075 gallons = 28.2075*cost per gallon
= 28.2075*3.89
= $109.727175
~= $109.73
therefore it takes approximately 109.73 dollars to travel 1,128.3 miles
to know more cost-related problems,
https://brainly.com/question/25109150
Calculate the unit rate. Label your work properly. Show your fraction work.
Math question : eating 3/4 pizza in 5/6 hour
Answers
Answer:
(9/10) of a pizza per hour.
Step-by-step explanation:
(3/4)*4=3
(5/6)*4= 3hr 20 mins
[3 (1/3)] / [3 (1/3)]=1
3 / [3 (1/3)]= 0.9
x. 1hr
x=3/4 •1 ÷ 5/6
x=3/4 • 6/5
x=18/20
x=9/10
Rate is 9/10 of pizza in one hour
A bag contains 5 black marbles, 7 blue marbles 3 green marbles 4 red marbles and 1 white marble. What is the probability of selecting a black marble then a red marble
Answers
Answer: The probability of selecting a black marble then a red marble would be 1/20
Step-by-step explanation: 5/20 x 4/20 = 1/4 x 1/5 = 1/20
Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.
Destiny owns a cake shop and she is working on two wedding cakes this week. The first cake consists of 4 small tiers and 4 large tiers, which will serve a total of 288 guests. The second one includes 3 small tiers and 5 large tiers, which is enough servings for 316 guests. How many guests does each size of tier serve?
A small tier will serve guests and a large tier will serve guests.
Answers
Answer:
small tier: 22large tier: 50Step-by-step explanation:
If cakes of 4 small and 4 large tiers serve 288 guests, and 3 small and 5 large tiers serve 316 guests, you want to know the number of guests served by a tier of each size.
SetupLet 's' and 'l' represent the numbers of guests served by small and large cake tiers, respectively. The first cake serves ...
4s +4l = 288
And the second cake serves ...
3s +5l = 316
SolutionSubtracting 3/4 of the first equation from the second gives ...
(3x +5l) -3/4(4s +4l) = (316) -3/4(288)
2l = 100
l = 50
4s +4(50) = 288 . . . substitute for l in the first equation
4s = 88 . . . . . . . . . . subtract 200
s = 22 . . . . . . . divide by 4
A small tier will serve 22 guests; a large tier will serve 50 guests.

The image of B translated using (x + 2, y + 3) would have what coordinates?

Answers
Answer:
(5, 4)
Step-by-step explanation:
(x + 2, y + 3)
Substitute x and y for that of B's position.(3 + 2, 1 + 3)
(5, 4)
Answer:
B' (5, 4 )
Step-by-step explanation:
the translation rule (x, y ) → (x + 2, y + 3 )
means add 2 to the original x- coordinate and add 3 to the original y- coordinate , then
B (3, 1 ) → B' (3 + 2, 1 + 3 ) → B' (5, 4 )
List the six (6) trigonometric ratios for the angle 2(pi)/3 using the unit circle.
Answers
The six trigonometric ratios are \(\sin{\theta}\\\), \(\cos{\theta}\), \(\tan{\theta}\\\), \(\csc{\theta}\\\), \(\sec{\theta}\\\), \(\cot{\theta}\\\)
\(\sin{\frac{2\pi}{3}} = \sin{\frac{\pi}{3}} = \frac{\sqrt{3}}{2}\\\cos{\frac{2\pi}{3}} = \cos{\frac{\pi}{3}} = \frac{1}{2}\\\tan{\frac{2\pi}{3}} = \tan{\frac{\pi}{3}} = \frac{\sin{\frac{\pi}{3}}}{\cos{\frac{\pi}{3}}} = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \frac{2\sqrt{3}}{2} = \sqrt{3}\\\csc{\frac{2\pi}{3}} = \csc{\frac{\pi}{3}} = \frac{1}{\sin{\frac{\pi}{3}}} = \frac{1}{\frac{\sqrt{3}}{2}} = \frac{2}{\sqrt{3}}} = \frac{2\sqrt{3}}{3}\\\)
\(\sec{\frac{2\pi}{3}} = \sec{\frac{\pi}{3}} = \frac{1}{\cos{\frac{\pi}{3}}} = \frac{1}{\frac{1}{2}} = \frac{2}{1} = 2\\\cot{\frac{2\pi}{3}} = \cot{\frac{\pi}{3}} = \frac{1}{\tan{\frac{\pi}{3}}} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}\)
An examination paper has 150 multiple-choice questions of one mark each, with each question having four choices. Each incorrect answer fetches -0.25 mark. Suppose 1000 students choose all their answers randomly with uniform probability. The sum total of the expected marks obtained by all these students is?
Answers
The sum of expected marks is given as follows:
9375.
How to obtain the expected marks?Each question has four choices, hence the probability of choosing the correct choice is given as follows:
p = 1/4 = 0.25.
Then the expected number of correct answers is given as follows:
E(X) = 0.25 x 150
E(X) = 37.5.
Then the expected grade for a single student is given as follows:
37.5 - 0.25(150 - 37.5) = 9.375.
The expected sum for the 1000 students is then given as follows:
1000 x 9.375 = 9375.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1
Cassie rolls a fair number cube with 6 faces labeled 1 through 6. She rolls the number cube 300 times. Which results are
probable to happen according to theoretical probability? Select TWO answers.

Answers
On solving the question, we can say that - the probability of given will be P(a/c) = 3/6 = 1/2
What is probability?A branch of mathematics known as probability measures the possibility of an event happening or a proposition being true. The probability of an occurrence is a number between 0 and 1, where roughly 0 denotes the event's improbability and 1 denotes certainty. A probability is a numerical representation of the possibility or probability that a specific event will take place. Probabilities can alternatively be stated as percentages ranging from 0% to 100%, or as percentages from 0 to 1. the proportion between the number of events in a comprehensive collection of equally likely outcomes that lead to a certain occurrence and the entire number of outcomes.
here,
the probability that event the dice will roll is 6
and chances of geting even numbers are = 3
so P(a/c) = 3/6 = 1/2
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ1
Resolva a inequação (x + 4)(x – 4) < 0.
Answers
Answer:
-4 < x < 4
Step-by-step explanation:

PLease help asap BRAINLIEST ANSWER
Given: line{AB}with point A (2,2) and the midpoint M( 4,-2)
Identify the coordinates of point `B.`
Given line `t` on the graph provided, choose all points that lie on the line that passes through point `P` and is perpendicular to line `t`.


Answers
Answer: (6,-6)
Step-by-step explanation:
To find the coordinates of point B, we can use the midpoint formula:
Midpoint formula: The midpoint M of a line segment with endpoints (x1, y1) and (x2, y2) is given by:
M = ((x1+x2)/2, (y1+y2)/2)
Here, we know that the midpoint M is (4, -2), and one endpoint A is (2, 2). Let B be the other endpoint, so we can use the midpoint formula to find B:
4 = (2+x2)/2 --> 8 = 2+x2 --> x2 = 6
-2 = (2+y2)/2 --> -4 = 2+y2 --> y2 = -6
Therefore, point B has coordinates (6, -6).
As for the second question, without a graph or information about the equation of line t and point P, it is not possible to determine which points lie on the line passing through P and perpendicular to t.