(9x10 to the 7th power) (7x10 to the 9th power) in scientific notation.
Answers
The value of the expression in scientific format is 6.3 x 10¹⁷
How to determine the expression in scientific format?From the question, we have the following parameters that can be used in our computation:
(9x10 to the 7th power) (7x10 to the 9th power)
To start with, we need to represent the above expression using numbers and mathematical operators
So, we have the following representation
(9 x 10⁷) (7 x 10⁹)
Next, we combine the brackets using a product sign
This gives
(9 x 10⁷) x (7 x 10⁹)
Next, we remove the brackets from the expression
This gives
9 x 10⁷ x 7 x 10⁹
Evaluate the products of 9 and 7
63 x 10⁷ x 10⁹
Apply the law of indices to evaluate the final products
63 x 10¹⁶
Rewrite as
6.3 x 10¹⁷
Hence, the solution is 6.3 x 10¹⁷
Read more about scientific notation at
https://brainly.com/question/27862246
#SPJ1
Related Questions
Select the correct answer from each drop-down menu.
The total area of the three triangles is
square units.
The area of the figure is
square units.
Answers
The total area of the three triangles is square units is 36 and the area of the figure is square units is 60.
What is the triangle?The triangle can be defined as a three-sided polygon in geometry, and it consists of three vertices and three edges. The sum of all the angles inside the triangle is 180°.
From the figure, the area of triangles can be calculated using the:
Area = (1/2)height×base length
Area of three triangle = 1/2(4×6) + 1/2(6×4) + 1/2(4×6)
Area of three triangle = 1/2(24×3) = 36 square units
Area of the figure = area of three triangle + area of the rectangle
= 36 + 6×4
= 60 square units
Thus, the total area of the three triangles is square units is 36 and the area of the figure is square units is 60.
Learn more about the triangle here:
brainly.com/question/25813512
#SPJ1

How many integers satisfy each inequality?
-102
Answers
Answer:At integers -2 and -3 the value of the equation is zero, hence satisfies the inequality. So overall 4 integers satisfy the inequality.
i got 1 2 3 4 5 6 7 8 ems in my bank account
Step-by-step explanation:
Somebody please help me ITS URGENT

Answers
Each ticket costs $37.5 according to the calculation t = ($175 - $25)/4.
What is the equation?Equation is a mathematical statement that expresses two expressions as equal. It consists of two expressions separated by an equal sign (=). An equation is used to solve for a unknown value by using known values and following the rules of algebra and arithmetic. Equations can be used to solve for a single unknown, multiple unknowns, and even non-numeric values.
Given that the total cost for parking and four tickets to a baseball game is $175.00.
$25 is the parking fee.
4 tickets cost $175 - $25.
Suppose that each ticket costs t.
t =($175 - $25)/4
Each ticket costs $37.5.
The equation follows.Each ticket costs $37.5 according to the calculation t = ($175 - $25)/4.
To know more about equation click-
http://brainly.com/question/2972832
#SPJ1
someone anwser this please

Answers
Square root 81 = one side length = 9m volume = 9^3 = 729
Harry owns a rare baseball card that is valued at $5.00. If he originally purchased the card for $2.00, by what percentage has its value increased?
Answers
Answer:
250 Percent
Step-by-step explanation:
First, you would have to find what percent of 2 is 5. So you would do 5/2 and that equals 2.5 or 250 Percent. (I think this is correct :))
Line u passes through points (10, 8) and (1, 10). What is the slope of line v?
Answers
\((\stackrel{x_1}{10}~,~\stackrel{y_1}{8})\qquad (\stackrel{x_2}{1}~,~\stackrel{y_2}{10}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{10}-\stackrel{y1}{8}}}{\underset{\textit{\large run}} {\underset{x_2}{1}-\underset{x_1}{10}}} \implies \cfrac{ 2 }{ -9 } \implies - \cfrac{2}{9}\)
Please help me and show work

Answers
Answer:
2/5
Step-by-step explanation:
If we convert 1/2 to tenths we get 5/10. We can subtract that from 9/10 to find out what q equals which will give us 4/10 which is also equal to 2/5
(sorry i'm really bad at explaining but I hope this helps)
Write a sequence of dilations and translations that maps circle D onto circle C and that shows the two circles you created are similar.
Answers
Answer: Circle d
Step-by-step explanation:
In August, the median home price in Auburn was $555,000 dollars. Since you want to buy an
"average" house, you find one for the median price and make a $55,000 down payment. Since current loan rates are 7.6% for a 30-year fixed rate mortgage, how much will your payment be each month (not counting insurance and taxes)? Round your answer to the nearest cent.
Answers
The monthly mortgage payment will be $3,373.16 (rounded to the nearest cent), excluding insurance and taxes.
We can apply the formula for a fixed-rate mortgage to determine the monthly mortgage payment:
\(M = P * (r * (1 + r)^n) / ((1 + r)^n - 1),\)
where:
M stands for the monthly payment, P for the principal (loan amount less the down payment), r for the monthly interest rate, which is calculated by dividing the yearly interest rate by 12, and n for the total number of monthly payments (30 years times 12 months).
The principal amount (P) is $555,000 - $55,000 = $500,000 if the median property price in Auburn is $555,000 and you put down $55,000.
The annual interest rate (r) is divided by 12 and converted to a decimal number to determine the monthly interest rate (r): 7.6% / 100 / 12 = 0.0063333.
The total number of monthly payments (n) is 30 years * 12 months = 360 months.
M = $500,000 * (0.0063333 * (1 + 0.0063333)^360) / ((1 + 0.0063333)^360 - 1).
The estimated monthly payment (M) using a calculator or spreadsheet is $3,373.16.
In conclusion, the monthly mortgage payment for a 30-year fixed rate mortgage at a 7.6% interest rate will be around $3,373.16 with a median property price in Auburn of $555,000 and a down payment of $55,000.
For more such question on insurance. visit :
https://brainly.com/question/29064772
#SPJ8
What is the area of the circle above?

Answers
Answer:
201.6
i think
Answer: I am pretty sure its A
Step-by-step explanation:
Put these numbers in order from least to greatest.
-1/4
2/40
-16
9/25
Answers
Answer:
(-1/4)(-16)(2/40)(9/25)Step-by-step explanation:
Enzo is making a scale drawing of the rectangle below.
A rectangle has a length of 8 centimeters and width of 5 centimeters.
Enzo says that he can draw an enlarged rectangle that is 16 centimeters by 13 centimeters. Which explains whether Enzo is correct?
Enzo is correct because he used a factor of 2 to enlarge the rectangle.
Enzo is correct because he doubled one dimension and added the two lengths to get the other dimension.
Enzo is not correct because the enlarged rectangle should be 16 centimeters by 5 centimeters.
Enzo is not correct because he did not multiply the length and width by the same factor.
Answers
Answer:
Step-by-step explanation:
D is it
Triangle ABC has vertices at A(−3, 3), B(0, 7), and C(−3, 0). Determine the coordinates of the vertices for the image if the preimage is translated 3 units up.
A′(−3, 0), B′(0, 4), C′(−3, −3)
A′(−3, 6), B′(0, 10), C′(−3, 3)
A′(−6, 3), B′(−3, 7), C′(0, 0)
A′(0, 3), B′(3, 5), C′(0, 0)
Answers
Answer:
To translate triangle ABC 3 units up, we need to add 3 to the y-coordinate of each vertex:
A' = (-3, 3 + 3) = (-3, 6)
B' = (0, 7 + 3) = (0, 10)
C' = (-3, 0 + 3) = (-3, 3)
Therefore, the coordinates of the vertices for the image triangle A'B'C' are A'(-3, 6), B'(0, 10), and C'(-3, 3).
So the correct answer is: A′(−3, 6), B′(0, 10), C′(−3, 3).
Find the errors and correct the following mathematical sentences.
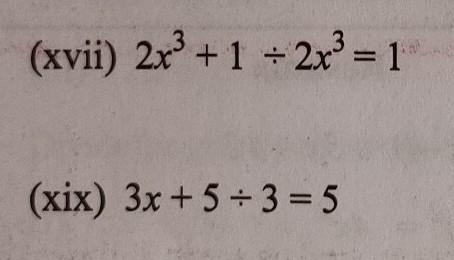
Answers
Answer:
This is your answer ☺️☺️☺️

Solve:(6x^2+5x+1)÷(x+2)
Answers
Answer:
6x+6x2+3
Step-by-step explanation:
6x2+5x+1+x+2
Combine 5x and x to get 6x.
6x2+6x+1+2
Add 1 and 2 to get 3.
6x2+6x+3
Find P(x)=−2x2+x6−4x+1 when x=−2.
Answers
Hey there!
p(x) = 2x^2 + x^4 - 4x + 1
y = 2x^2 + x^4 - 4x + 1
y = 2(-2)^2 - 2^4 - 4(-2) + 1
y = -4^2 - 16 - 4(-2) + 1
y = 8 - 16 - (-8) + 1
y = - 8 - (-8) + 1
y = 0 + 1
y = 1
Therefore, your answer is: y = 1
Good luck on your assignment and enjoy your day!
~Amphitrite1040:)

What is the average rate of change on the interval from 3 to 9?
Enter your answer in the grid below. Make sure your answer contain

Answers
Answer:
5
Step-by-step explanation:
Consider the expression below.
9+ 4(x + 2) - 3x
Select the term that best describes "3" in the given expression.
A. exponent
B. coefficient
c. constant
D. variable
Answers
Answer:
es D
Step-by-step explanation:
es una variable porque lleva una letra o un símbolo en esa caso representa una cantidad esa letra
Solve for x.
Show work

Answers
Answer:
x=11.34
Step-by-step explanation:
Multiply -5.4 in both sides
x = 11.34
Have a good day ^^
A set of data has a normal distribution with a mean of 55 and a standard deviation of 9. Find the percent of data within the following interval.
from 28 to 82
The percent of data within the given interval is.
(Type an integer or a decimal.)
Answers
The percent of data within the following interval from 28 to 82 is 99.73%
Calculating the percent of data of values from the the z-scoresFrom the question, we have the following parameters that can be used in our computation:
Mean = 55
Standard deviation = 9
Scores = from 28 to 82
So, we have
z = (28 - 55)/9 = -3
z = (82 - 55)/9 = 4
This means that it is between a z-score of -3 and a z-score of 3
This is represented as
Probability = (-3 < z < 3)
Using a graphing calculator, we have
Probability = 0.9973
Express as percentage
Probability = 99.73%
Hence, the probability is 99.73%
Read mroe about z-scores at
brainly.com/question/25638875
#SPJ1
Teo makes a necklace of x wooden beads at $0.50 each and 6 glass beads at $1.25 each. The average cost of the beads in the necklace is $0.75. Write an equation to model the situation.
Answers
Answer:
0.50x + 7.50 = 0.75(x+6)
Hope this helps :)
The equation to model the situation of x is (0.5x + 7.5) = 0.75(x + 6)
What is the equation?The equation is the defined as mathematical statements that have a minimum of two terms containing variables or numbers is equal.
Given data as :
There are x wooden beads at $0.50 each necklace.
There are 6 glass beads at $1.25 each necklace.
Since the cost of the beads in a necklace is addition of wooden beads and glass beads.
So, 0.50x + 6*1.25 = 0.5x + 7.5 dollars
There are (x+6) beads.
Consider that the beads usually cost $0.75 each
(0.5x + 7.5)/(x+6) = 0.75
0.5x + 7.5 = 0.75(x+6)
0.5x + 7.5 = 0.75x + 4.5
7.5 - 4.5 = 0.75x - 0.5x
3 = 0.25x or
0.25x = 3
x = 3/0.25
x = 12
Hence, the equation to model the situation of x is (0.5x + 7.5) = 0.75(x + 6)
Learn more about equation here:
brainly.com/question/10413253
#SPJ6
contains (1,1) and has a shape of f(x)=2x^2 vertex is on the y axis
Answers
ANSWER
| x=0
Step-by-step explanation:
f(x) = 2x²
Rewrite the function by completing the
square
f(x)
= 2x²
Find the symmetry
X = 0
Write the equation of a line perpendicular to the one above that passes through (-2, 9). You may use either slope intercept or point slope form.

Answers
Answer:
-3x + 3
Step-by-step explanation:
To find the equation of a line perpendicular to the line passing through (-2, 1) and (4, 3), we need to determine the slope of the original line first. Then, we can use the negative reciprocal of that slope to find the slope of the perpendicular line. Finally, we can use the point-slope form to write the equation of the perpendicular line.
Step 1: Find the slope of the original line.
Slope (m) = (change in y) / (change in x)
m = (3 - 1) / (4 - (-2))
m = 2 / 6
m = 1/3
Step 2: Determine the slope of the perpendicular line.
The slope of the perpendicular line is the negative reciprocal of the original line's slope.
Perpendicular slope = -1 / (1/3)
Perpendicular slope = -3
Step 3: Use the point-slope form to write the equation.
The point-slope form is given by:
y - y1 = m(x - x1)
Using the point (-2, 9) and the perpendicular slope (-3), we can write the equation as:
y - 9 = -3(x - (-2))
y - 9 = -3(x + 2)
y - 9 = -3x - 6
y = -3x + 3
Therefore, the equation of the line perpendicular to the line passing through (-2, 1) and (4, 3) and passing through (-2, 9) is y = -3x + 3.
Help plz I was stuck on this question for 1 week

Answers
In the diagram, there is a half circle so the circumference would be πr.
Now plug in the radius of 3 to get
Area of circle = 3π or 9.425.
Add 10 to that from the perimeter of the triangle.
Final answer = 19.425
An engineer is going to redesign an ejection seat for an airplane. The seat was designed for pilots weighing between 130 lb and 181 lb. The new population of pilots has normally distributed weights with a mean of 140 lb and a standard deviation of 27.3 lb.
Required:
a. If a pilot is randomly selected, find the probability that his weight is between 150 lb and 201 lb. The probability is approximately__________.
b. If 39 different pilots are randomly selected, find the probability that their mean weight is between 150 lb and 201 lb. The probability is approximately__________.
c. When redesigning the ejection seat which probability is more relevant
Answers
Answer:
(a) The probability that his weight is between 150 lb and 201 lb is 0.3428.
(b) The probability that the sample mean weight is between 150 lb and 201 lb is 0.011.
(c) When redesigning the ejection seat, the probability of a single pilot is more relevant as discussed in part (a).
Step-by-step explanation:
We are given that the seat was designed for pilots weighing between 130 lb and 181 lb.
The new population of pilots has normally distributed weights with a mean of 140 lb and a standard deviation of 27.3 lb.
Let \(\bar X\) = sample mean price for a movie in the United States
SO, X ~ Normal(\(\mu=140,\sigma^{2} =27.3^{2}\))
(a) The z-score probability distribution for the normal distribution is given by;
Z = \(\frac{ X-\mu}{\sigma}} }\) ~ N(0,1)
where, \(\mu\) = population mean weights = 140 lb
\(\sigma\) = standard deviation = 27.3 lb
Now, the probability that his weight is between 150 lb and 201 lb is given by = P(150 lb < X < 201 lb) = P(X < 201 lb) - P(X \(\leq\) 150 lb)
P(X < 201 lb) = P( \(\frac{ X-\mu}{\sigma}} }\) < \(\frac{ 201-140}{27.3}} }\) ) = P(Z < 2.23) = 0.9871
P(X \(\leq\) 150 lb) = P( \(\frac{ X-\mu}{\sigma}} }\) \(\leq\) \(\frac{ 150-140}{27.3}} }\) ) = P(Z \(\leq\) 0.37) = 0.6443
The above probability is calculated by looking at the value of x = 2.23 and x = 0.37 in the z table which has an area of 0.9871 and 0.6443.
Therefore, P(150 lb < X < 201 lb) = 0.9871 - 0.6443 = 0.3428.
(b) Let \(\bar X\) = sample mean weight
The z-score probability distribution for the sample mean is given by;
Z = \(\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }\) ~ N(0,1)
where, \(\mu\) = population mean weight = 140 lb
\(\sigma\) = standard deviation = 27.3 lb
n = sample of pilots = 39
Now, the probability that the sample mean weight is between 150 lb and 201 lb is given by = P(150 lb < \(\bar X\) < 201 lb) = P(\(\bar X\) < 201 lb) - P(\(\bar X\) \(\leq\) 150 lb)
P(\(\bar X\) < 201 lb) = P( \(\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }\) < \(\frac{201-140}{\frac{2.73}\sqrt{39} } }\) ) = P(Z < 13.95) = 0.9999
P(\(\bar X\) \(\leq\) 150 lb) = P( \(\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }\) \(\leq\) \(\frac{150-140}{\frac{2.73}\sqrt{39} } }\) ) = P(Z \(\leq\) 2.29) = 0.9889
Therefore, P(150 lb < \(\bar X\) < 201 lb) = 0.9999 - 0.9889 = 0.011.
(c) When redesigning the ejection seat, the probability of a single pilot is more relevant as discussed in part (a) because it is important to look after the safety of each and every pilot not of a particular sample.
What values of b satisfy 3(2b + 3)² = 36?
Answers
Answer:
The values of b that satisfy the equation are:
b = (2√3 - 3) / 2
b = (-2√3 - 3) / 2
In other words, b can take the values (2√3 - 3) / 2 or (-2√3 - 3) / 2.
Step-by-step explanation:
To find the values of b that satisfy the equation 3(2b + 3)² = 36, we can solve for b by following these steps:
1. Divide both sides of the equation by 3:
(2b + 3)² = 12
2. Take the square root of both sides:
√[(2b + 3)²] = √12
Simplifying further:
2b + 3 = ±√12
3. Subtract 3 from both sides:
2b = ±√12 - 3
4. Divide both sides by 2:
b = (±√12 - 3) / 2
Simplifying further:
b = (±√4 * √3 - 3) / 2
b = (±2√3 - 3) / 2
Therefore, the values of b that satisfy the equation are:
b = (2√3 - 3) / 2
b = (-2√3 - 3) / 2
In other words, b can take the values (2√3 - 3) / 2 or (-2√3 - 3) / 2.
A researcher is investigating whether a difference exists in the mean weight of green-striped watermelons grown on two different farms: one that uses organic methods and one that uses nonorganic methods. The mean and standard deviation of the weights in a random sample of 43 watermelons from the organic farm were 18 pounds and 2 pounds, respectively. The mean and standard deviation of the weights in a random sample of 40 watermelons from the nonorganic farm were 20 pounds and 1.7 pounds, respectively.
Required:
What represents the standard error of the difference in the mean weights of watermelons from the two farms?
Answers
Answer:
D. 2^2+1.7^243+40−−−−−√
Step-by-step explanation:
The computation is shown below:
Given that
Sample 1
n_1 = 43
mean = 18
s_1 = 2
Sample 2
n_2 = 40
mean = 20
s_2 = 1.7
Now the standard error is
\(= \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} } \\\\= \sqrt{\frac{2^2}{43} + \frac{1.7^2}{40} }\)
= 0.4065
SOLVE FAST I NEED HELP PLEASE FASTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTT

Answers
Answer:
36
Step-by-step explanation:
27/3=9
9*4=36
find all the missing measurement

Answers
Given:
\(\Delta CAP\sim \Delta DAY\)
To find:
The value of FD.
Solution:
We have, \(\Delta CAP\sim \Delta DAY\). So, the corresponding angles are congruent.
\(\angle CAP\cong \angle DAY\)
\(\angle ACL\cong \angle AD F\) (Given in the figure)
Two angles are congruent. So,
\(\Delta CAL\sim \Delta DA F\)
Corresponding sides of similar triangles are proportional. So,
\(\dfrac{CA}{DA}=\dfrac{LC}{FD}\)
Substituting the given values from the figure, we get
\(\dfrac{35}{21}=\dfrac{25}{FD}\)
\(\dfrac{5}{3}=\dfrac{25}{FD}\)
On cross multiplication, we get
\(5\times FD=3\times 25\)
\(5FD=75\)
Divide both sides by 5.
\(FD=\dfrac{75}{5}\)
\(FD=15\)
Therefore, the measure of FD is 15 units.
x/3 =-8 x=? what does x =?
Answers
Answer: -24
Step-by-step explanation:
\(\frac{x}{3}=-8\\\frac{x}{3}(3)=-8(3)\\ x=-24\)