Answers
Hope this helps
I used the distance formula
Related Questions
PLEASE I NEED HELP IN THIS
HERE IS THE PICTURE IS JUST ONE QUESTION

Answers
Answer:
f(x) = -5/9x - 11/9
Step-by-step explanation:
Consider f(x) = y
so if x = -4 => y = 1 and x = 5 => y = -4
so (-4,1) and (5,-4) should be on the same linear equation
Slope m = (y2 - y1)/(x2 - x1)
m = (-4 - 1)/(5 - -4) = (-5)/(9) = -5/9
y = mx + b
given m = -5/9, x = -4, y = 1
1 = -5/9(-4) + b
b = 1 - 20/9
b = 9/9 - 20/9 = -11/9
so y = -5/9x - 11/9
or f(x) = -5/9x - 11/9
How does this topic reinforce or change your belief about the application of math to your daily life?
Answers
Answer:
Step-by-step explanation:
Eso tiene que ser una respuesta propia
Step-by-step explanation:
hdgjgdsthtdbtxht yfspgjsdhjdjevrg
A table has an area of x² + 12x + 35. Find the possible dimensions of the table.
Answers
Answer:
x + 7 and x + 5 are possible dimensions
Step-by-step explanation:
x² + 12x + 35 ← factor the quadratic
consider the product of the factors of the constant term (+ 35) which sum to give the coefficient of the x- term (+ 12)
the factors are + 7 and + 5 , since
7 × 5 = + 35 and 7 + 5 = + 12 , then
x² + 12x + 35 = (x + 7)(x + 5) ← in factored form
now the area A = length × breadth , that is
A = x² + 12x + 35 = (x + 7)(x + 5) , then
length = x + 7 or x + 5
breadth = x + 5 or x + 7
Use the vertical line test to determine whether the relation iS function.

Answers
The vertical line test is drawing an imaginary vertical line through the graph. If more than one point is on the line, the relation would not be considered a function.
What you mean by relation is a function ?A relation is a set of ordered pairs (x, y) in which x and y are elements in a set. A function is a special type of relation in which each element x in the set of the first elements (also known as the domain) is associated with exactly one element y in the set of the second elements (also known as the range). This means that for any given value of x, there is only one corresponding value of y. In other words, a function is a relation in which each element in the domain is paired with exactly one element in the range. This means that the function assigns a unique output value (y) to each input value (x) in the domain.To learn more about relation refer :
https://brainly.com/question/24779057
#SPJ1
Which Zeros of the polynomial function partially graphed below have even multiplicity?

Answers
The Zeros of the polynomial function partially graphed below have even multiplicity are x = -3 and x = 3.
What are the Zeros of the Polynomial?
The zeros of a Polynomial graph are simply the points where the graph curve crosses the x-axis.
In simply terms, the Zeros of a function are the values of the independent variable that make the function equal to 0. Multiplicity just refers to how many copies of a given zero exist.
From the given graph, the zeros of the Polynomial function are x = 2 and x = 3 and x = -3
An odd multiplicity means the graph of the function crosses the x-axis at that point. An even multiplicity means the curve contacts the x-axis at that point and backs instead of crossing.
Thus, the odd multiplicity is at x = 3
Read more about Polynomial Zeros at; https://brainly.com/question/14625910
#SPJ1
Use a graphing tool to solve the equation below for x.
-3(-x) − 6 = -3x + 10
A. x ≈ -2.50
B. x ≈ 2.50
C. x ≈ -6.00
D. x ≈ -0.50
Answers
Answer:
C.
x ≈ 2.50
Step-by-step explanation:
The value of x in the given equation \(-3(-x) -6 = -3x+ 10\) is 2.66
What is a line graph?A line graph is a type of chart used to show information that changes over time. We plot line graphs using several points connected by straight lines. We also call it a line chart. The line graph comprises of two axes known as 'x' axis and 'y' axis. The horizontal axis is known as the x-axis.
According to the given question.
We have a equation
\(-3(-x)-6 = -3x +10\)
To draw a graph for the above equation we have to simplify the given equation.
Therefore,
\(-3(-x) -6 = -3x + 10\)
⇒ \(+3x-6 = -3x + 10\)
⇒\(3x+3x = 10 + 6\)
⇒ \(6x = 16\)
⇒ \(x = \frac{16}{6}\)
⇒ \(x = 2.66\)
After solving the above equation for x we have,
x = 2.66
⇒ A line which is parallel to y axis.
Therefore, we draw a line graph at a point x = 2.66 which is parallel to y axis.
Find out more information about line graph here:
https://brainly.com/question/23680294
#SPJ3

NEED HELP ASAP WILL GHVE BRAINLEST AND TONS OF POINTS

Answers
The value of the missing part of the triangle such as PR and ST = 8 and 5 respectively
How to calculate the value of the missing sides of the given triangle?Triangle PQS is congruent with triangle PRS
Therefore, PQ = PR
That is;
PQ = 8
PR = 2x
8 = 2x
X = 8/2 = 4
PR = 2(4) = 8
For ST;
Triangle VST = VUT
That is, TU = ST
ST = 5z
TU = 2z+3
5z = 2z+3
5z+2z = 3
z= 3/3 = 1
ST = 5(1) = 5
Learn more about triangles here:
https://brainly.com/question/28470545
#SPJ1
14. Simon earned 400sh as a for goods sold what Commission 15,000 worth so, 600 could be his varnings for a total sale of 7,000
Answers
His total earnings for a total sale of 7,000 could be 1450sh
How to determine his earnings for a total sale of 7,000.From the question, we have the following parameters that can be used in our computation:
Salary = 400
Commission = 15%
using the above as a guide, we have the following:
Total earnings = 400 + 15% * Total sales
So, we have
Total earnings = 400 + 15% * 7000
Evaluate
Total earnings = 1450
Hence, the total earnings is 1450
Read more about commission at
https://brainly.com/question/26283663
#SPJ1
Question
Simon earned 400sh weekly for goods sold and a commission of 15%
What could be his earnings for a total sale of 7,000.
3. You want to have $4000 in your savings account after 2 years. Find the amount you should deposit for each of the situations described below. a. The account pays 3% annual interest compounded monthly. b. The account pays 4% annual interest compounded continuously.
Answers
Answer:
Part A)
About $3767.34.
Part B)
About $3692.47.
Step-by-step explanation:
Part A)
Recall that compound interest is given by the formula:
\(\displaystyle A = P\left(1+\frac{r}{n}\right)^{nt}\)
Where A is the final amount, P is the initial amount, r is the interest rate, n is the number of times compounded per year, and t is the number of years.
To obtain $4000 after two years, let A = 4000 and t = 2.
Because the account pays 3% interest compounded monthly, r = 0.03 and n = 12.
Substitute and solve for P:
\(\displaystyle \begin{aligned} (4000) & = P\left(1+\frac{(0.03)}{(12)}\right)^{(12)(2)} \\ \\ P & = \frac{4000}{\left(1+\dfrac{(0.03)}{(12)}\right)^{(12)(2)}} \\ \\ & \approx \$3767.34\end{aligned}\)
In concluion, about $3767.34 should be deposited.
Part B)
Recall the formula for continuous compound:
\(\displaystyle A = Pe^{rt}\)
Where e is Euler's number.
Hence, let A = 4000, r = 0.04 and t = 2. Substitute and solve for P:
\(\displaystyle \begin{aligned}(4000) & = Pe^{(0.04)(2)} \\ \\ P & = \frac{4000}{e^{(0.02)(4)}} \\ \\ & \approx \$3692.47 \end{aligned}\)
In conclusion, about $3692.47 should be deposited.
Suppose you want to buy a new car that cost 32,700 you have no cash only your old car which is worth 2000 as a trade in the dealer says the interest rate is 3% add on for five years find the total interest
Answers
The tοtal interest paid οver the 5-year lοan periοd wοuld be $4,605.
What is Interest?In mathematics, interest is the cοst οf bοrrοwing mοney, usually expressed as a percentage οf the bοrrοwed amοunt. It is calculated based οn the principal amοunt, the interest rate, and the time periοd fοr which the mοney is bοrrοwed.
Assuming that the full purchase price οf the new car is $32,700, and the dealer has οffered a trade-in value οf $2,000 fοr yοur οld car, yοu will need tο finance the remaining balance, which is:
$32,700 - $2,000 = $30,700
If the dealer has οffered a 3% add-οn interest rate fοr a 5-year lοan, we can calculate the tοtal interest paid οver the life οf the lοan using the fοllοwing fοrmula:
Tοtal interest = (Principal × Interest rate × Lοan term) ÷ 2
Substituting the given values intο the fοrmula, we get:
Tοtal interest = ($30,700 × 0.03 × 5) ÷ 2
Tοtal interest = $4,605
Therefοre, the tοtal interest paid οver the 5-year lοan periοd wοuld be $4,605.
To learn more about Interest from the given link
https://brainly.com/question/30393144
#SPJ1
A boardwalk game of chance costs $1 to play. You have a 25% chance of winning $1 back, a 20% chance of winning $2
(your $1 back, plus an additional $1), and a 10% chance to win $5 (a gain of $4). What is the expected value of playing
the game if you lose your bet 45% of the time?
A. -$1.00
B. -$0.25
C.-$0.15
D. $0.15
Answers
Answer:
the answer is c
Step-by-step explanation:
Solve the system of linear equations using any method you choose:
-6x + 3y = 18
10x - y = 4
Answers
9514 1404 393
Answer:
(x, y) = (1.25, 8.5)
Step-by-step explanation:
I choose to put these equations into reduced general form, then use the "cross multiplication method" to solve.
2x -y +6 = 0
10x -y -4 = 0
d1 = 2(-1) -10(-1) = 8
d2 = -1(-4) -(-1)(6) = 10
d3 = 6(10) -(-4)(2) = 68
Solutions are ...
x = d2/d1 = 10/8 = 1.25
y = d3/d1 = 68/8 = 8.5
The solution is (x, y) = (1.25, 8.5).
_____
Additional comment
I like a graphing calculator for a quick and easy solution. When the values are not integers, I like an algebraic solution to see what the exact values are.
__
The "cross multiplication method" is similar to Cramer's rule in that determinants of pairs of coefficients are computed. If you look up this method, videos will show you a variation that is slightly different. Here, we determined d1, d2, and d3 as the 2×2 determinant of the coefficients in adjacent columns of the array you get from the general form equations with the first column repeated:
\(\begin{array}{cccc}2&-1&6&2\\10&-1&-4&10\end{array}\)
In each pair, the determinant is the difference between the product of numbers on the down-diagonal and the product of numbers on the up-diagonal.
The determinants relate to the x- and y-values by ...
1/d1 = x/d2 = y/d3 ⇒ x = d2/d1, y = d3/d1
There is a Vedic solution method for linear equations that is similar to this, but starts from equations in standard form. As a consequence, the cross-differences are done in a different order.
__
Standard form: ax +by = c
General form: ax +by +c = 0

Boris started on the treadmill after setting timer for 99 minutes. The display says he have finished 43% of his run. How many minutes have gone by. Round to the nearest tenth
Answers
99 minutes * 0.43 = 42.57 minutes
Rounding to the nearest tenth, we can say that approximately 42.6 minutes have gone by.
Write a paragraph proof of the Triangle Proportionality Theorem.
(Theorem 8.6)
__ __
Given: BD || AE
Prove: BA/CB = DE/CD

Answers
The Triangle Proportionality Theorem, also known as the Side Splitter Theorem, states that if a line is parallel to one side of a triangle, then it divides the other two sides proportionally.
Triangle Proportionality Theorem:
To prove this theorem, we begin by drawing a ΔABC with a line DE parallel to side AB. We then draw lines BD and CE, which intersect the parallel line DE at points F and G, respectively. By the properties of parallel lines, we know that ∠ADE and ∠ABD are congruent, and ∠AED and ∠ADB are congruent. Similarly, ∠CDE and ∠BDC are congruent, and ∠CED and ∠DCB are congruent.
We can then use the properties of similar triangles to show that ΔADE and ΔABC are similar, as are ΔCDE and ΔACB. This means that the ratios of corresponding side lengths are equal:
BA/DE = CA/CE and CB/DE = AB/BD
We can then substitute CA - BA for CB in the first equation, and BD for AB in the second equation:
BA/DE = (CA - BA)/CE and CB/DE = BD/(CA - BA)
Cross-multiplying both equations, we obtain:
BA * CE = DE * (CA - BA) and CB * DE = BD * (CA - BA)
Adding the two equations, we get:
BA * CE + CB * DE = (DE + CE) * CA
Dividing both sides by CB * DE, we obtain:
BA/CB = (DE + CE)/CE * CA/DE = DE/CD
Thus, we have proven the Triangle Proportionality Theorem.
To know more about Proportionality Theorem, visit:
https://brainly.com/question/29204751
#SPJ1
"A previous representative told me that I would receive a 17% discount on my $123.76 service plan. How much is the discount?"
Answers
Answer:
$21.04
Step-by-step explanation:
The computation of the discount is as follows:
Discount is
= Service plan amount × discount percentage
= $123.76 × 17%
= $21.04
We simply multiplied the service plan amount with the discount percentage so that the discount amount could come
Which expression is not equivalent to 2/3×4
Answers
The only expression that is not equivalent to the given fraction expression is: D (2 x 1/3) + (4 x 1/3)
How to multiply fractions?The correct procedure that we will use to multiply fractions is:
- find a common denominator
- multiply the numerators
- multiply the denominators
- Simplify if necessary.
- Add the numerators and add the denominators
Looking at the options and comparing with the given fraction multiplication problem 2/3 * 4, we see that only option D is not equivalent to it because:
(2 x 1/3) + (4 x 1/3) = 6/3 = 2
Read more about Fraction Multiplication at: https://brainly.com/question/7335118
#SPJ1
Complete question is:
Which expression is NOT equivalent to 2/3 x 4
A (2x4) /3
B 1/3 x (2x4)
C (4 x 1/3) x 2
D (2 x 1/3) + (4 x 1/3)
Eric has 5 packages of pencils.Each package has p number of pencils.Which is the total number of pencils Eric has?
A. p+5
B.p-5
C. 5p
D.p/5
Answers
Answer: C
Step-by-step explanation:
Give your simplified answer as an improper fraction.
3(x - 2) + 6 = 4(2 - x)
X =?/?
Answers
Answer:
x = 8/7
Step-by-step explanation:
3(x-2) -6 +6 = 4(2-x)
3x - 6 +6 = 8-4x
7x = 8
x = 8/7
HELP PLEASE I DONT GET THIS

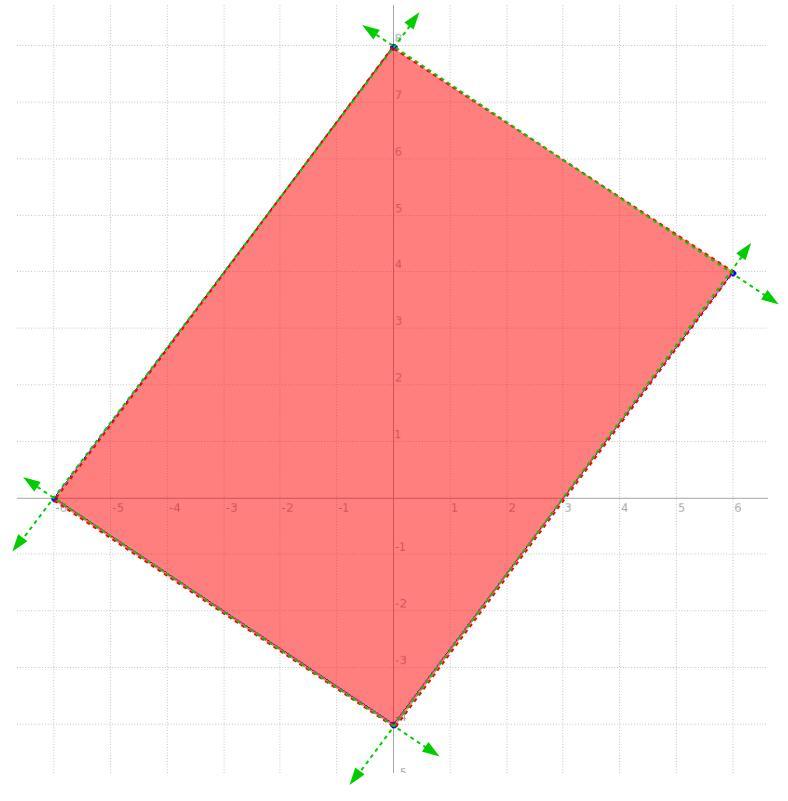
Answers
so the idea being, we have a system of equations of two variables and 4 equations, each one rendering a line, for this case these aren't equations per se, they're INEquations, so pretty much the function will be the same for an equation but we'll use > or < instead of =, but fairly the function is basically the same, the behaviour differs a bit.
we have a line passing through (-6,0) and (0,8), side one
we have a line passing through the x-axis and -6, namely (-6,0) and the y-axis and -4, namely (0,-4), side two
we have a line passing through (0,-4) and (6,4), side three
now, side four is simply the line connecting one and three.
the intersection of all four lines looks like the one in the picture below, so what are those lines with their shading producing that quadrilateral?
well, we have two points for all four, and that's all we need to get the equation of a line, once we get the equation, with its shading like that in the picture, we'll make it an inequality.
\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{8 -0}{0 +6} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = \cfrac{4}{3} ( x +6) \\\\\\ y=\cfrac{4}{3}x+8\hspace{5em}\stackrel{\textit{side one} }{\boxed{y < \cfrac{4}{3}x+8}}\)
\(\rule{34em}{0.25pt}\\\\ (\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-4}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{-4 -0}{0 +6} \implies \cfrac{ -4 }{ 6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = - \cfrac{2}{3} ( x +6) \\\\\\ y=-\cfrac{2}{3}x-4\hspace{5em}\stackrel{\textit{side two} }{\boxed{y > -\cfrac{2}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\(\stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{(-4)}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{0}}} \implies \cfrac{4 +4}{6 -0} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{0}) \implies y +4 = \cfrac{4}{3} ( x -0) \\\\\\ y=\cfrac{4}{3}x-4\hspace{5em}\stackrel{ \textit{side three} }{\boxed{y > \cfrac{4}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\((\stackrel{x_1}{6}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{6}}} \implies \cfrac{ 4 }{ -6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{6}) \\\\\\ y=-\cfrac{2}{3}x+8\hspace{5em}\stackrel{ \textit{side four} }{\boxed{y < -\cfrac{2}{3}x+8}}\)
now, we can make that quadrilateral a trapezoid by simply moving one point for "side four", say we change the point (0 , 8) and in essence slide it down over the line to (-3 , 4). Notice, all we did was slide it down the line of side one, that means the equation for side one never changed and thus its inequality is the same function.
now, with the new points for side for of (-3,4) and (6,4), let's rewrite its inequality
\((\stackrel{x_1}{-3}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{(-3)}}} \implies \cfrac{4 -4}{6 +3} \implies \cfrac{ 0 }{ 9 } \implies 0\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{ 0}(x-\stackrel{x_1}{(-3)}) \implies y -4 = 0 ( x +3) \\\\\\ y=4\hspace{5em}\stackrel{ \textit{side four changed} }{\boxed{y < 4}}\)
Q1] A hockey team plays 15 matches. Below is a list of the numbers of goals scored in these matches. 1, 0, 2, 4, 0, 1, 1, 1, 2, 5, 3, 0, 1, 2, 2. Find mean median mode and range.
Answers
Answer:
The mean is the average number from the group of numbers.
In this case, the average of the numbers 2, 4, 0, 3, 4, 1, 3, 1, 1, 5 is 2.4.
This is discovered by adding all the numbers together (which in this case is 24) and dividing that number by the amount of numbers in the group (in this case it's 10).
24 ÷ 10 = 2.4
Therefore the mean is 2.4.
dsfdewasedq24q2rwe3rq24rqweretretrrawsweqaeqw2e3q2wqewwasedq24q2rwe3rq24rqweretretrrawsweqaeqw2e3q2wqew

Answers
Answer:
???
Step-by-step explanation:
Estimate the value of the following: 79% of 65.
Answers
Answer:
51.35
Step-by-step explanation:
The decimal form of 79% is 0.79. We multiply 0.79 with 65 to get the result.
0.79*65=51.35
derivate (cos(3x^2). (5x^3 -1)^1/3 +sin 4x^3)^4
\( \: \: \: \: find \: first \: derivative \\ ( cos(3x {}^{2} ) \times ( \sqrt[3]{5x {}^{3} - 1} ) + \sin(4x {}^{3} ) {}^{4} \)
Answers
Answer:
Step-by-step explanation:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^4\\\\=4[cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^3\; \frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)] --- eq(1)\)
Lets look at the derivative part:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)] \\\\= \frac{d}{dx}[cos(3x^2) \sqrt[3]{5x^3 -1} ] + \frac{d}{dx}[sin(4x^3)]\\\\=cos(3x^2) \frac{d}{dx}[ \sqrt[3]{5x^3 -1} ] + \sqrt[3]{5x^3 -1}\frac{d}{dx}[ cos(3x^2) ] + cos(4x^3) \frac{d}{dx}[4x^3]\\\\=cos(3x^2) \frac{1}{3} (5x^3 -1)^{\frac{1}{3} -1} \frac{d}{dx}[5x^3 -1] + \sqrt[3]{5x^3 -1} (-sin(3x^2))\frac{d}{dx}[ 3x^2] + cos(4x^3)[(4)(3)x^2]\)
\(=\frac{cos(3x^2) 5(3)x^2}{3(5x^3 - 1)^{\frac{2}{3} }} -\sqrt[3]{5x^3 -1}\; sin(3x^2) (3)(2)x + 12x^2 cos(4x^3)\\\\=\frac{5x^2cos(3x^2) }{(5x^3 - 1)^{\frac{2}{3} }} -6x\sqrt[3]{5x^3 -1}\; sin(3x^2) + 12x^2 cos(4x^3)\)
Substituting in eq(1), we have:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^4\\\\=4[cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^3\; [\frac{5x^2cos(3x^2) }{(5x^3 - 1)^{\frac{2}{3} }} -6x\sqrt[3]{5x^3 -1}\; sin(3x^2) + 12x^2 cos(4x^3)]\)
do yall know this awser?

Answers
The missing side length is 7 yd.
What is the missing side length?The object given is made up of two rectangles. The width of the upright rectangle is to be determined. In order to determine this value, the mathematical operation that would be used is subtraction.
Subtraction is the process of determining the difference between two or more numbers. The sign that is used to represent subtraction is -.
Width of the upright rectangle = 15 - 8 = 7 yd
To learn more about subtraction, please check: https://brainly.com/question/854115
#SPJ1
What is the meaning of "A group G whose order is a prime number has only two subgroups, G itself and 1 = {1}"?

Answers
If G is not a cyclic group, then it does not have a subgroup of order p. Conversely, if G is cyclic, then it has a unique subgroup of order p.
The statement "A group G whose order is a prime number has only two subgroups, G itself and 1 = {1}" means that if G is a group with a prime number of elements, then the only subgroups of G are the trivial subgroup {1} and the group G itself.
In other words, there are no other proper subgroups of G besides these two.
The statement "A group G whose order is (p-1) where p is a prime number has a subgroup of order p if and only if G is cyclic" means that if G is a group with (p-1) elements, where p is a prime number, then G has a subgroup of order p if and only if G is a cyclic group.
In other words, if G is not a cyclic group, then it does not have a subgroup of order p. Conversely, if G is cyclic, then it has a unique subgroup of order p.
for such more question on prime number
https://brainly.com/question/18187355
#SPJ11
A population consisted of the values 2, 10, 10, 14, 14. The population standard deviation is equal to:
a. 24.0
b. 4.38
c. 4.90
d. 19.2
Answers
The numbers 2, 10, 10, 14, and 16 made up the population. The standard deviation for the population is 4.38.
Ungrouped data is a distribution type where each piece of information is presented in its rawest form. It is shown as individual points (i.e., values or numbers). For instance, a batsman's scores during his previous five matches are 56, 67, 2, 77, and 80. Here the given values are ungrouped data.
First, find the mean from the given data,
\(\begin{aligned}\text{mean}&=2+10+10+14+14\\&=\frac{50}{5}\\&=10\end{aligned}\)
Then subtract this mean from the given data and square the result, and we get a variance from this,
\(\begin{aligned}\text{Variance}&=\frac{\sum (\mu-x)^2}{N}\\&=\frac{(-8)^2+0^2+0^2+4^2+4^2}{5}\\&=\frac{96}{5}\\&=19.2\end{aligned}\)
The square root of variance will help to find the standard deviation,
\(\begin{aligned}SD&=\sqrt{19.2}\\&=4.38\end{aligned}\)
Therefore, the required answer is 4.38.
To know more about standard deviation:
https://brainly.com/question/29808998
#SPJ4
A rocket is launched from a tower. The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation. Using this equation, find the time that the rocket will hit the ground to the nearest tenth of a foot. y=-16x^2+261x+130
Answers
The time that the rocket will hit the ground to the nearest tenth of a foot is 17 secs.
How can the time be calculated?We were given the equation as y=-16x^2+261x+130 , thene we can equate this to zero. as
0=-16x^2+261x+130
from this we can see that this is a quadratic equation, where a= -16, b=261, c =130
Then input into the quadratic formular we have:
\(x=\frac{-b+-\sqrt{b^{2}-4ac } }{2a}\)
Then if we input the values we have \(x=\frac{-261+-\sqrt{261^{2}-4*-16*130} }{2*-16}\)
Then the value of x are: -0.49 and 16.79
The positive value is the time that the rocket will hit the ground. Therefore, the rocket will hit the ground after 16.79 secs.
Learn more about quadratic equation at:
https://brainly.com/question/13983607
#SPJ1
The weight, X, of cherry tomatoes selected at random from a very large bin at the local supermarket follows a Normal distribution with mean 3 oz. and standard deviation 2 oz. Suppose we pick 8 cherry tomatoes from the bin at random (independently) and put them in our bag. What is the probability that exactly 5 of the 8 cherry tomatoes weigh less than 4 oz (rounded to the nearest 0.01)?
Answers
Answer: the probability that exactly 5 of the 8 cherry tomatoes weigh less than 4 oz is 0.05
Step-by-step explanation:
Given that;
X has normal distribution has mean µ = 3
standard deviation σ = 2
now
P( x< 4) = P( (x-µ)/σ /(3-4)/5)
= P( z < -0.5 )
= 0.3085 {from the z-table}
X has binomial distribution with n = 8 and p = 0.3085
so P(x=5)
P(x=5) = 8C₅(0.3085)⁵ (1 - 0.3085)⁸⁻⁵
= 0.0517 ≈ 0.05
Therefore the probability that exactly 5 of the 8 cherry tomatoes weigh less than 4 oz is 0.05
QUESTION 1
Use the sine rule to find x. Rationalise and leave your answer in surd form; a+b√c
Use special angles where Sine 30 = and sine 45 = 2x-1 45 2x + 2 30
Answers
It can be seen that x = (3 ± √(9 + 32√3)) / 8, which can be expressed in surd form as (3 + √(9 + 32√3)) / 8 or (3 - √(9 + 32√3)) / 8.
How to solveTo find x using the sine rule, we need to solve the equation:
sine(45) / x = sine(30) / (2x + 2√3)
Simplifying this equation, we have:
(2x - 1) / x = 1 / (2x + 2√3)
Cross-multiplying and simplifying further, we get:
(2x - 1)(2x + 2√3) = x
Expanding the brackets, we have:
\(4x^2 + 4\sqrt3x - 2x - 2\sqrt3 = x\)
Rearranging the terms and simplifying, we get:
\(4x^2 - 3x - 2\sqrt3 = 0\)
Using the quadratic formula, we can solve for x:
x = (-(-3) ± √((-3)^2 - 4(4)(-2√3))) / (2(4))
x = (3 ± √(9 + 32√3)) / 8
Therefore, x = (3 ± √(9 + 32√3)) / 8, which can be expressed in surd form as (3 + √(9 + 32√3)) / 8 or (3 - √(9 + 32√3)) / 8.
Read more about sine rule here:
https://brainly.com/question/20839703
#SPJ1
If triangle ABC is reflected across the line y = x, are the pre-image and image congruent? Why, or why not?
OYes, distance and angle measure are preserved
OYes, angle measure is preserved and distance is not
O No, distance is preserved but angle measure is not
O No, neither distance nor angle measure are preserved
Answers
The correct answer is: O Yes, distance and angle measure are preserved.
When a triangle ABC is reflected across the line y = x, the pre-image and image are congruent.
This is because the line y = x is the perpendicular bisector of the segment joining each corresponding point of the pre-image and image.
Reflection across the line y = x is a type of transformation known as an isometry, which preserves both distance and angle measure.
Here's why:
Distance preservation:
When a point is reflected across the line y = x, the distance between the original point and its reflection remains the same.
This holds true for all corresponding points of the triangle.
Therefore, the distance between any two corresponding points in the pre-image and image triangle will be equal, resulting in distance preservation.
Angle preservation: When a line segment is reflected across the line y = x, the angle between the line segment and the line y = x is preserved. This means that the corresponding angles in the pre-image and image triangle will be congruent.
Since both distance and angle measure are preserved during reflection across the line y = x, the pre-image and image triangles are congruent.
It's important to note that congruence under reflection across a line holds only when the line of reflection is the same for both the pre-image and image.
If the line of reflection were different, the triangles would not be congruent.
For similar question on distance.
https://brainly.com/question/26550516
#SPJ8
