Answers
Related Questions
x/6−7=12 what is x
if its a good enough answer I WILL GIVE BRAINLIEST
Answers
Answer:
x/6=12+7
x/6=19
x=19*6
x=114
Select the statement that best justifies the conclusion based on the given information.
Ifx+5 = 15, then x=10.
O addition property of equality
O subtraction property of equality
multiplication property of equality
O substitution
Answers
Answer:
B.
Subtraction property of equality.
(Don’t send me a link pls just answer!) First 3 people to answer get lots of points pls do it by friday!
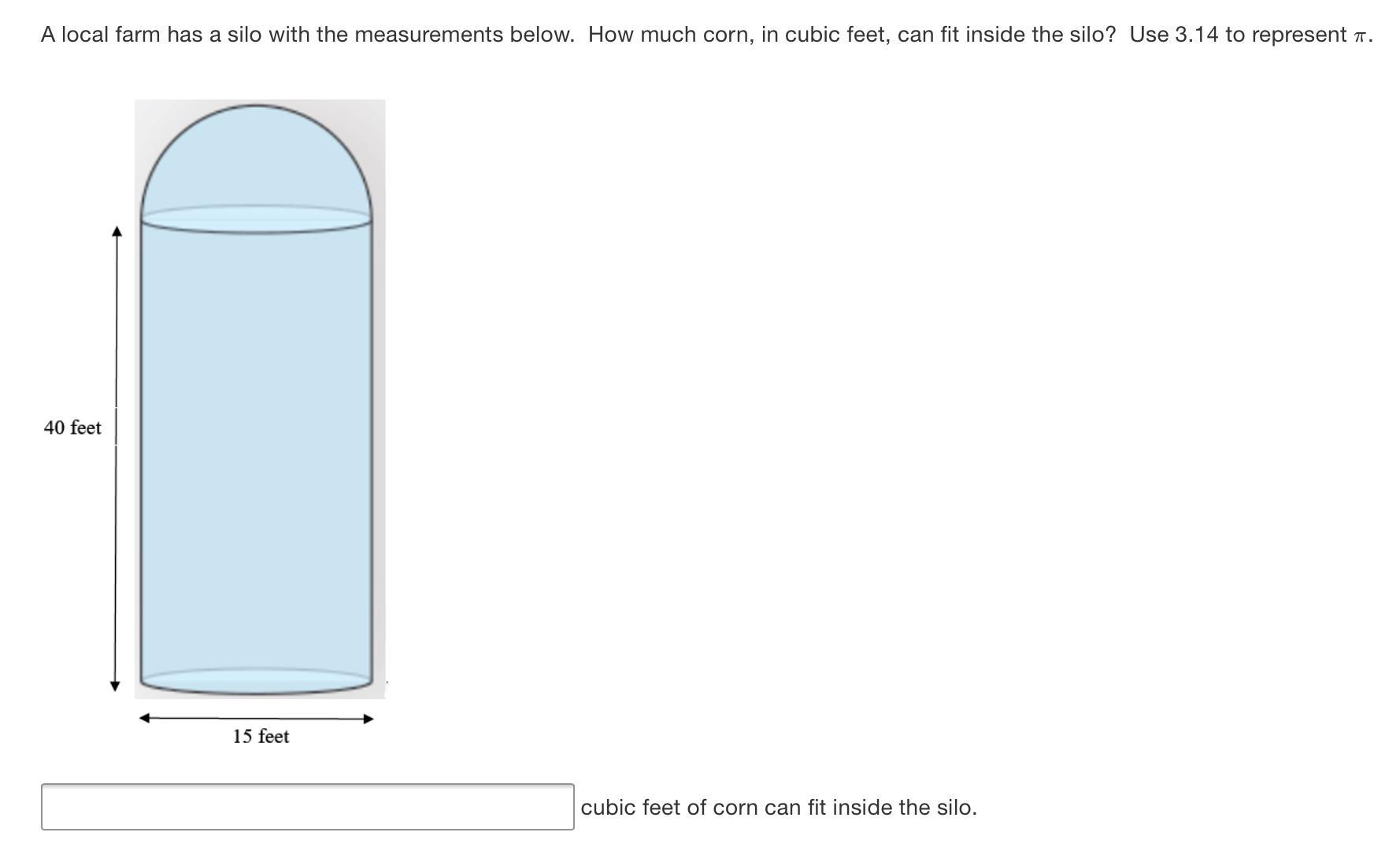
Answers
Answer:
8835.73ft^3
Step-by-step explanation:
First:
Find area of the base circle.
Diameter is 15, so radius is 7.5
Area of the base circle is 56.25pi (use formula: A=pi(r)^2 ) (also ill convert pi into decimals only later)
next find the volume of the cylinder
height is 40 so volume = 56.25pi*40 = 2250pi
next find the volume of the dome at the top.
you know the radius is 7.5
Use volume of sphere formula below :
4 /3πr^3
=1767.15
alright now add the two bolded values
1767.15+2250pi
= 8835.73
hope this helps
An indoor staircase has a 14 inch vertical rise per step to get to the second floor of the house. If the angle of elevation is 47 degrees and there are 13 feet of horizontal space total for each of the landings
combined, answer the following questions showing each step of your work:
a) What is the landing space per step (in inches, rounded to the nearest inch)?b) Find the vertical rise from the 1st floor to the 2nd floor (in feet, rounded to the nearest foot).
Answers
The landing space per step for the indoor staircase is solved to be
13 inchesThe vertical rise from first floor to second floor is 14 feet
How to find the landing spaceThe figure defined to be a right triangle and the dimensions are worked using SOH CAH TOA
Sin = opposite / hypotenuse - SOH
Cos = adjacent / hypotenuse - CAH
Tan = opposite / adjacent - TOA
The right angle triangle comprises of
opposite = total vertical height
adjacent = total horizontal height = 13 feet
The total vertical height is calculated using tan, TOA
let the angle be x
tan x = opposite / adjacent
tan 47 = opposite / 13
opposite = (13 * tan 47) feet
opposite = 12 * (13 * tan 47) inch
opposite = 167.2895 inch
For a 14 inch vertical rise per step say number of step is y
14 y = total vertical height
14 y = 167.2895
y = 11.9493 steps ≈ 12 steps
The landing space for 12 steps is solved by
= horizontal space total in inch / number of steps
= 13 * 12 / 12
= 13 inches
vertical rise from the 1st floor to the 2nd floor
opposite = (13 * tan 47) feet
opposite = 13.94 feet
opposite = 14 feet (to the nearest foot)
Learn more about SOH CAH TOA here:
https://brainly.com/question/29402966
#SPJ1
jannete has 326 pennies, 64 nickles, and 15 dimes. if she has to exchange her coins for dollars how many dollars will she have ? how many cents will remain?
Answers
Answer:
She will have 7 dollars, with 96 cents remaining.
Step-by-step explanation:
326 pennies is $3.26
64 nickels is $3.20
15 dimes is $1.50
Add them all;
$3.26 + $3.20 + $1.50 = $7.96
She will have 7 dollars, with 96 cents remaining
A car travels 56 miles in 3.5 hours.
a. What is the unit rate?
b. How long will it take the car to travel 120 miles?
c. How far will the car travel in 6 hours?
Answers
B = 7.5 hours
C = 96 miles
Step by step explanation:
A: If the car travels 56 miles in 3.5 hours you divide the 56 miles by the 3.5 hours and then you will get your unit rate of 16 miles per hour.
B: Now that you know that your unit rate is 16 miles per hour you can figure out how long it will take the car to travel 120 miles. To find this answer all you have to do is divided the amount the car traveled, 120 miles, by the unit rate, 16 miles per hour. After doing the division you will get your answer of 7.5 hours/ 7 hrs and 30 mins.
C: This one is pretty simple. All you have to do is take your unit rate of 16 and multiply it by the 6 hours. After doing your multiplication you will get your answer of 96 miles.
I hope you understand and this answered all of your questions. :)
Solve the equation.
t-12=3
Answers
Answer:
t = 15
Step-by-step explanation:
t - 12 = 3
t = 3 + 12
t = 15
Hope this helps
Stacy is selling tickets to the school play. The tickets are $7 for adults and $4 for children she sells twice as many adult tickets as children’s tickets and brings in a total of $270. How many of each kind of ticket did she sell?
Answers
Stacy sold 15 children tickets and 30 adult tickets.
The tickets are $7 for adults and $4 for children.
She sells twice as many adult tickets as children tickets and bring in a total of $270.
Therefore,
let
number of children ticket sold = x
number of adult ticket sold = 2x
7(2x) + 4(x) = 270
14x + 4x = 270
18x = 270
x = 270 / 18
x = 15
The number of children ticket sold = 15
The number of adult ticket sold = 15 × 2 = 30
learn more about algebra here: https://brainly.com/question/14569336?referrer=searchResults
solve for the interval [0,2pi): 1+sin θ= (√3+2)/2
Answers
Answer:
Step-by-step explanation:
1+sin(θ)=√3/2+2/2
sin(θ) = √3/2
on unit circle this is where y is positive because sin so it will be pi/3 and 2pi/3
Add the following polynomials, then place the answer in the proper location on the grid. Write your answer in descending powers of x.
x 4 -3x + 1, 4x 2 - 2x + 8, and x 3 - 9
Answers
The addition of the polynomials x⁴ - 3x + 1, 4x² - 2x + 8, x³ - 9 in descending powers of x is x⁴ + x³ + 4x² - 5x.
Polynomialx⁴ - 3x + 14x² - 2x + 8x³ - 9Adding the polynomial
(x⁴ - 3x + 1) + (4x² - 2x + 8) + (x³ - 9)
Open parenthesis= x⁴ - 3x + 1 + 4x² - 2x + 8 + x³ - 9
Collect like terms in descending powers= x⁴ + x³ + 4x² - 3x - 2x + 1 + 8 - 9
= x⁴ + x³ + 4x² - 5x
Therefore, the addition of the polynomials x⁴ - 3x + 1, 4x² - 2x + 8, x³ - 9 in descending powers of x is x⁴ + x³ + 4x² - 5x.
Learn more about polynomial:
https://brainly.com/question/1401895
#SPJ1
100 yojan=how much km?
Answers
Answer:
100 yojan=how much km
1287.48
please brainlist
For what value of 2 will the function f(x), be continuous at x=0?
(See Image) Thanks

Answers
(i) \(\lim_{x \to \pi/3}\) f(x) = 1 + √3.
(ii) \(\lim_{x \to \frac{\pi}{4}} f(x)\) does not exist.
For λ = 2.5, the function f(x) will be continuous at x = 0.
Given the function is,
f(x) = 1.5, when x = 0
= 1 -2 sin x, when x < π/4
= 1 + 2 sin x, when x > π/4
= 1 + (sin λx/sin 5x)
Now,
\(\lim_{x \to \pi/3}\) f(x) = \(\lim_{x \to \pi/3}\) (1 + 2 sin x) [Since, π/3 > π/4]
= 1 + 2 sin (π/3)
= 1 + 2√3/2 = 1 + √3
Hence, \(\lim_{x \to \pi/3}\) f(x) = 1 + √3.
Now left hand limit is,
\(\lim_{x \to \frac{\pi^+}{4}}\) f(x) = \(\lim_{x \to \frac{\pi^+}{4}}\) (1 + 2sin x) = 1 +2 sin(π/4) = 1 + 2*(1/√2) = 1 + √2
and right hand limit is,
\(\lim_{x \to \frac{\pi^-}{4}}\) f(x) = \(\lim_{x \to \frac{\pi^-}{4}}\) (1 - 2 sin x) = 1 - 2*(1/√2) = 1 - √2
Since left hand limit and right hand limit are not equal so value of \(\lim_{x \to \frac{\pi}{4}} f(x)\) does not exist.
\(\lim_{x \to 0}\) f(x) = \(\lim_{x \to 0}\) (1 + (sin λx/sin 5x)) = 1 + \(\lim_{x \to 0}\) ((sin λx/λx)/(sin 5x/5x))*(λ/5) = 1 + λ/5
Since f(x) is continuous at x = 0.
So, \(\lim_{x \to 0}\) f(x) = f(0)
1 + λ/5 = 1.5
λ/5 = 1.5 - 1 = 0.5
λ = 2.5
Hence the value of λ will be 2.5.
To know more about continuous here
https://brainly.com/question/27761372
#SPJ1
60 POINT QUESTION. Middle school math, ordered pairs.

Answers
Answer:
(0,2)
(3,0)
Step-by-step explanation:
(3,0)
Is the correct answer
What is the distance between the points (7,5) (4,9)
Answers
The Distance will be 5.
The distance between two points is the length of the line segment connecting the two points on the plane. The formula for finding the distance between two points is usually d=√((x2 – x1)² + (y2 – y1)²). This formula is used to find the distance between any two points on the coordinate or x-y plane.
Let point (7,5) be A and point (4,9) be B
Distance formula =
Ab = √(x1- x2) ² + (y1 -y2) ²
Then Distance AB will be
Ab = √(7-4) ² + (5 -9) ²
= √ 3² + 4²
= √ 9 + 16
= 5
Hence the distance will be 5.
Learn more distance between the points at :
https://brainly.com/question/15958176
The points \((7,5)\) \((4,9)\) are separated by a distance of \(5\) units.
The distance between the two points is given by the length of the segment between them.
The Distance Formula is a helpful tool for figuring out how far apart two points are when they are arbitrarily represented on a coordinate plane as points A\((x_{1},y_{1})\) and B\((x_{2},y_{2})\).
The Pythagorean Theorem is essentially the source of the Distance Formula. Calculating the right triangle's hypotenuse's length is the fundamental purpose of the distance formula.
Use the distance formula to get the distance between two places.
\(d = \sqrt{ (x_{2} - x_{1})^{2} +(y_{2} - y_{1})^{2} }\)
In the posted query,
\((x_{1},y_{1})=(7,5)\\\\(x_{2},y_{2})=(4,9)\)
Distance formula,
\(d = \sqrt{ (x_{2} - x_{1})^{2} +(y_{2} - y_{1})^{2} }\)
\(d = \sqrt{ (4-7)^{2} +(9-5)^{2} }\)
\(d = \sqrt{ (-3)^{2} +(4)^{2} }\)
\(d = \sqrt{ 9+16 }\)
\(d = \sqrt{ 25 }\)
\(d = 5\)
Therefore, the points \((7,5)\) \((4,9)\) are at a distance of \(5\) units.
For more information about Distance Formula: https://brainly.com/question/7245260
From the choices below, choose an expression that is equivalent to the expression:
22/-4
A. (-22|-4 )
B. 22|4
C. -(22|-4)
D. -(22|4)
Answers
Answer: b
Step-by-step explanation:
Determine which set of side measurements could be used to form a triangle.
3, 5, 11
4, 18, 23
5, 9, 14
7, 12, 18
Answers
The set of side measurement could be used to form a triangle is option(4) 7, 12 and 18
If the sides of the triangles are a, b and c. There will be three condition
a + b > c
b + c > a
c + a > b
We have to check these condition
Part 1
The sides are 3, 5 and 7
3 + 5 > 11
8 < 11
It does not form a triangle
Part 2
The sides are 4, 18 and 23
4+18 >23
22 < 23
It does not form a triangle
Part 3
The sides are 5, 9 and 14
5+9 > 14
14 = 14
It does not form a triangle
Part 4
The sides are 7, 12 and 18
7+12 > 18
19 > 18
12 + 18 > 7
30 > 7
7+18 > 12
25 > 12
It forms a triangle
Hence, the set of side measurement could be used to form a triangle is option(4) 7, 12 and 18
Learn more about triangle here
brainly.com/question/2773823
#SPJ1
Can someone help me please?
ASAP

Answers
Answer:
y = 12 x = 12\(\sqrt{3}\)
Step-by-step explanation:
This is a 60, 90, 30. It's a special triangle.
2z = 24
z = 12
If x = z\(\sqrt{3}\)
then x = 12\(\sqrt{3}\)
y = z itself
So y = 12

Find the angle on the unit circle

Answers
The angle on the unit circle is solved to be
56.01 degrees (to the nearest tenth)
How to find the angleTo find the angle of the terminal side through the given point on the unit circle, we can use the inverse trigonometric functions.
given that P = ((√5)/4, (√11)/4)
θ = arctan ((√11)/4 / (√5)/4)
θ = arctan((√11)/(√5))
θ ≈ 56.01 degrees
hence to the nearest tenth of a degree, the angle of the terminal side through the point P = ((√5)/4, (√11)/4) on the unit circle is approximately 56.01 degrees.
Learn more about unit circle at
https://brainly.com/question/30403151
#SPJ1
Analyze the key features of the graph of shown below. f (x)
(-2,-1) (-4,-3)
Use rules of transformations and the parent function to formulate an equation for the rational function shown in the graph.Show all your work.
Answers
The answer of the given question based on the Analyze the key features of the graph the answer is the equation of the line shown in the graph is f(x) = -x - 3, and the equation for the transformed rational function is:
f(x) = 1/(x + 5) - 3.
What is Rational Function?A rational function is function that can be expressed as quotient of two polynomial functions, where denominator polynomial is not zero. It has general form:
f(x) =P(x)/Q(x)
where P(x) and Q(x) are the polynomial functions in x, and Q(x) ≠ 0 for all values of x in function's domain.
Using the point-slope form, we can find the slope of the line as follows:
slope = (change in y) / (change in x) = (-3 - (-1)) / (-4 - (-2)) = -1
Then, we can choose one of the points and plug it into the point-slope form:
y - (-1) = -1(x - (-2))
Simplifying, we get:
y + 1 = -x - 2
we can rearrange the equation to slope-intercept form:
y = -x - 3
Therefore, the equation of the line shown in the graph is f(x) = -x - 3.
The general equation for a rational function is f(x) = a/(x-h) + k, where a, h, and k are constants that determine the vertical stretch/compression, horizontal shift, and vertical shift, respectively.
Using the given points, we can write two equations to solve for a and h:
(-1) = a/(-2 - h) + k
(-3) = a/(-4 - h) + k
Simplifying each equation, we get:
(-1) = a/(-2 - h) + k => k = (-h - a - 2)/a
(-3) = a/(-4 - h) + k => k = (-h - 3a - 4)/a
Setting the two expressions for k equal to each other and solving for h, we get:
(-h - a - 2)/a = (-h - 3a - 4)/a
-h - a - 2 = -h - 3a - 4
2a = 2
a = 1
Substituting a = 1 into one of the equations for k, we get:
k = (-h - 1 - 2)/1
k = -h - 3
So, the equation for the transformed rational function is:
f(x) = 1/(x - h) - 3
To find h, we can substitute one of the given points into the equation and solve for h. Let's use (-2, -1):
-1 = 1/(-2 - h) - 3
2 + 3 = -2 - h
h = -5
Therefore, the equation for the transformed rational function is:
f(x) = 1/(x + 5) - 3
To know more about Slope-intercept form visit:
https://brainly.com/question/18314949
#SPJ1
The equation of the line shown in the graph is f(x) = -x - 3, and the equation for the transformed rational function is f(x) = 1/(x + 5) - 3.
What is Rational Function?A rational function is function that can be expressed as quotient of two polynomial functions, where denominator polynomial is not zero. It has general form:
f(x) =P(x)/Q(x)
where P(x) and Q(x) are the polynomial functions in x, and Q(x) ≠ 0 for all values of x in function's domain.
Using the point-slope form, we can find the slope of the line as follows:
slope = (change in y) / (change in x) = (-3 - (-1)) / (-4 - (-2)) = -1
Then, we can choose one of the points and plug it into the point-slope form:
y - (-1) = -1(x - (-2))
Simplifying, we get:
y + 1 = -x - 2
we can rearrange the equation to slope-intercept form:
y = -x - 3
Therefore, the equation of the line shown in the graph is f(x) = -x - 3.
The general equation for a rational function is f(x) = a/(x-h) + k, where a, h, and k are constants that determine the vertical stretch/compression, horizontal shift, and vertical shift, respectively.
Using the given points, we can write two equations to solve for a and h:
(-1) = a/(-2 - h) + k
(-3) = a/(-4 - h) + k
Simplifying each equation, we get:
(-1) = a/(-2 - h) + k => k = (-h - a - 2)/a
(-3) = a/(-4 - h) + k => k = (-h - 3a - 4)/a
Setting the two expressions for k equal to each other and solving for h, we get:
(-h - a - 2)/a = (-h - 3a - 4)/a
-h - a - 2 = -h - 3a - 4
2a = 2
a = 1
Substituting a = 1 into one of the equations for k, we get:
k = (-h - 1 - 2)/1
k = -h - 3
So, the equation for the transformed rational function is:
f(x) = 1/(x - h) - 3
To find h, we can substitute one of the given points into the equation and solve for h. Let's use (-2, -1):
-1 = 1/(-2 - h) - 3
2 + 3 = -2 - h
h = -5
Therefore, the equation for the transformed rational function is:
f(x) = 1/(x + 5) - 3
To know more about Slope-intercept form visit:
https://brainly.com/question/18314949
#SPJ1
The complete question is as follows:
Analyze the key features of the graph of shown below. f (x)
(-2,-1) (-4,-3)
Use rules of transformations and the parent function to formulate an equation for the rational function shown in the graph. Show all your work.

Convert 40 miles per hour to feet per second.
Answers
Answer:
Step-by-step explanation:
58.6667
Answer:
The answer is 58.6667
please find the value of x in the figure

Answers
Answer:
Step-by-step explanation:
E is the midpoint of Ac & D is the midpoint of AB
DE = (1/2)BC {Midpoint theorem}
\(x +1 = \dfrac{1}{2}(4x - 6)\\\\\\ Multiply \ the \ whole \ equation \ by 2\\\\ 2*(x+1) =2*\dfrac{1}{2}*(4x - 6)\)
2*x + 2*1 = 4x - 6
2x + 2 = 4x - 6
Add 6 to both sides
2x + 2 + 6 = 4x
2x + 8 = 4x
Subtract 2x from both sides
8 = 4x - 2x
2x = 8
Divide both sides by 2
x = 8/2
x = 4
Which of the following is a radical equation?
x+ square root 5 = 12
x² = 16
3+ square root 7 = 13
7 square root x = 14

Answers
Answer:
7 square root x = 14
Step-by-step explanation:
A radical equation will have the variable inside the radical
Answer:
D
Step-by-step explanation:
A radical equation persists when a radical includes a variable within it. In this case the x is in the radical, times 7. The rest of the answers do not have a variable in a radical.
Anyone help with this

Answers
Answer:
Anyone help with this
x = 3t / b3 6 9 12 15 18 21 24 27 30 is odd or even numbers?
Answers
Answer: Half of them are even and half of them are odd.
Step-by-step explanation:
The even numbers are 6, 12, 18, 24, and 30. An even number is defined as a number that is divisible by 2, meaning it has no remainder when divided by 2. For example, 6 divided by 2 equals 3 with no remainder, so 6 is even.
The odd numbers are 3, 9, 15, 21, and 27. An odd number is defined as a number that is not divisible by 2, meaning it has a remainder of 1 when divided by 2. For example, 9 divided by 2 equals 4 with a remainder of 1, so 9 is odd.
Therefore, out of the given numbers, half of them are even and half of them are odd.
________________________________________________________
A data set consisting of newborn baby weight is normally distributed with a mean of 8.5 pounds in standard deviation of 0.5 pounds
Answers
SOLUTION
By the empirical rule, the 68% will lies between
\((\bar{x}-\sigma,\bar{x}+\sigma)\)Where
\(\bar{x}=8.5\text{ and }\sigma=0.5\)68% will lies between the interval
\(\begin{gathered} (8.5-0.5,8.5+0.5) \\ (8.0,9.0) \end{gathered}\)For the percentage that lies between 7.5 and 9.5 we will have
\(\begin{gathered} 7.5=8.5-1=8.5-2(0.5)=\bar{x}-2\sigma \\ 9.5=8.5-1=8.5+2(0.5)=\bar{x}+2\sigma \end{gathered}\)According to the empirical rule,
\(\text{ 95\% of the data falls in the interval }(7.5,9.5)\)Therefore 95% will lies between 7.5 and 9.7 pounds
For the percentage that lies between 7 and 10 we will have
\(\begin{gathered} 7=8.5-1.5=8.5-3(0.5)=\bar{x}-3\sigma \\ 10=8.5+1.5=8.5+3(0.5)=\bar{x}+3\sigma \end{gathered}\)According to the empirical rule,
\(\text{ 99.7\% of the data falls in the interval }(7,10)\)Therefore 99.7% lies between 7 and 10 pounds
2x+3y=6
−4x+3y=12
Answers
The best way to start off this question is to get rid of the y value as the y value is already equal in both equations. T\(-1\)o get rid of the y value, subtract the 2 equations together.
\(6x=-6\)
\(x=-1\)
Now that you have solved x, you can replace any x value (from either equation). In this scenario, the first equation is easier to solve for the y value.
\(2(-1)+3y=6\\-2+3y=6\\3y=8\\y=\frac{8}{3}\)
Thus,
x = \(-1\) and y = \(\frac{8}{3}\); \((-1,\frac{8}{3} )\)
Hope this helped :)
A 16 foot ladder is propped up against the roof of a house. The angle of elevation is 62 degrees. How tall is the house?
Answers
Answer is below.
Let's call the height of the house "h".
The ladder is propped up against the house, forming a right triangle with the wall of the house and the ground. The ladder is the hypotenuse of the triangle, and the height of the house is one of the legs.
We know that the length of the ladder is 16 feet, and the angle of elevation is 62 degrees. We can use trigonometry to find the height of the house.
The trigonometric function that relates the angle of elevation to the height and length of the ladder is the tangent function:
tan(62) = h/16
To solve for h, we can multiply both sides by 16:
16 tan(62) = h
Using a calculator, we can evaluate the tangent of 62 degrees to get:
16 tan(62) ≈ 28.6
So the height of the house is approximately 28.6 feet.
IF Y = e ^ (- 3x) then prove that (d ^ 2 * y)/(d * x ^ 2) + (dy)/(dx) - 6y = 0

Answers
Step-by-step explanation:
dy/dx = -3e^(-3x) = -3y
d^2y/dx^2 = 9e^(-3x) = 9y
The equality becomes
-3y +9y -6y = 0
Which is true, 0=0
Vehicles generally decrease in value around 14% per year. If you buy a vehicle priced at $39,500 , this can be modeled by the equation A=39500(0.86)t . Estimate the value of the vehicle after 4 years. Round to the nearest cent and do not round until the final calculation.
Answers
Rounding to the nearest cent, the estimated value of the vehicle after 4 years is approximately $23,726.20..
To estimate the value of the vehicle after 4 years, we can use the given equation A = 39500(0.86)^t, where A represents the value of the vehicle and t represents the number of years.
Substituting t = 4 into the equation:
A = 39500(0.86)^4
A ≈ 39500(0.5996)
A ≈ 23726.20
Rounding to the nearest cent, the estimated value of the vehicle after 4 years is approximately $23,726.20.
This estimation is based on the assumption that the vehicle's value decreases by 14% each year. The equation A = 39500(0.86)^t models the exponential decay of the vehicle's value over time. By raising the decay factor of 0.86 to the power of 4, we account for the 4-year period. The final result suggests that the value of the vehicle would be around $23,726.20 after 4 years of ownership.
For more such questions on estimated value
https://brainly.com/question/27898355
#SPJ8
MATHEMATICS
1. If each interior angle of a regular polygon is five times the exterior angle, how many sides has the polygon? x° зх°6x° 4xº 4x° 2x⁰ 2. Find the value of X in the polygon drawn above.
Answers
1. The number of sides of the polygon is 8
2. The value of x is 36
What is a polygon?A polygon can be defined as a flat or plane. The sum of a regular polygon is expressed as (n-2)180. The sum of exterior angle of a polygon is 360.
Therefore the sum of the interior is 5 times the exterior.
(n-2)180 = 5×360
180n - 360 = 1800
180n = 1800-360
180n = 1440
divide both sides by 180
n = 1440/180
n = 8
therefore the number of sides of the polygon is 8
2. The number of sides of the polygon is 6
Therefore the sum of angle in the polygon = 6-2)180 = 4× 180
= 720°
x+3x+6x+4x+4x+2x = 720
20x = 720
x = 720/20
x = 36
therefore the value of x is 36
learn more about polygon from
https://brainly.com/question/1592456
#SPJ1
