A box contains 16 square chips, 12 triangular chips, and 4 circular chips. Identify the ratio of circular chips to square chips in all three forms.
Answers
The ratio of circular chips to square chips is 1:4.
What is a ratio?The ratio is a numerical relationship between two values that demonstrates how frequently one value contains or is contained within another.
Given:
A box contains 16 square chips, 12 triangular chips, and 4 circular chips.
The ratio of circular chips to square chips,
= Circular chips / square chips
= 4 / 16
= 1/4
= 1: 4
Therefore, the ratio is 1:4.
To learn more about the ratio;
https://brainly.com/question/13419413
#SPJ1
Related Questions
Which inequality is equivalent to the given inequality? -4(x+7)< 3(x-2)
Answers
An equivalent inequality to the given \(-4(x + 7) < 3(x - 2)\) is \(7x > -22.\)
To find an equivalent inequality, we can start by simplifying the given inequality and then make adjustments to preserve its truth.
Let's simplify the given inequality step by step:
\(-4(x + 7) < 3(x - 2)\)
Expanding both sides:
\(-4x - 28 < 3x - 6\)
Grouping like terms:
\(-4x - 3x < -6 + 28\)
Simplifying:
\(-7x < 22\)
To maintain the direction of the inequality, we need to multiply both sides by -1.
However, when we multiply or divide both sides of an inequality by a negative number, the direction of the inequality is reversed.
Therefore, we need to flip the inequality sign:
\(7x > -22\)
Hence, an equivalent inequality to the given \(-4(x + 7) < 3(x - 2)\) is
\(7x > -22.\)
For such more questions on inequality
https://brainly.com/question/30238989
#SPJ8
May someone please help me with this im very confused on how to solve this

Answers
Answer:
4y - 5x + 7 = 0
Step-by-step explanation:
To get to the equation of its perpendicular, firstly we'll need the slope of this line.
\( \boxed{ \mathfrak{slope = \red{ \mathsf{ \frac{y_{2} - y _{1}}{x_{2} - x _{1}} }}}}\)
(x1, y1) and (x2, y2) are any two points kn the given line.
I caught two points that lie on this graph, and they are :
(-2, 2)(8, -6)\( \mathsf{ \implies \: slope = \frac{y_{2} - y _{1}}{x_{2} - x _{1}} }\)
\(\mathsf{ \implies \: slope = \frac{ - 6- 2}{8 - ( - 2)} }\)
\(\mathsf{ \implies \: slope = \frac{ -8}{8 + 2} }\)
(two minus make a plus)
\(\mathsf{ \implies \: slope = \frac{ -8}{10} }\)
\(\mathsf{ \implies \: slope = \frac{ \cancel{-8} {}^{ \: \: - 4} }{ \cancel{10} \: \: {}^{5} } }\)
slope = -4 /5
That's the slope of the given line.
Now, the slope of the line perpendicular to this one will be equal to its negative reciprocal.
slope (perpendicular) = 5/ 4
and they've given a point that lies in the perpendicular, it is = (3, 2)
For equation of a line thru a point, we have:
\( \boxed{ \mathsf{ \red {y} - {y}^{1} = slope \times (\red{x} - {x}^{1} }) }\)
the letters in red are the variables that won't be changed thruout.
and (x¹, y¹) are the points on the line.
(x¹, y¹) = (3, 2) slope = 5/ 4\( \implies \mathsf{y - 2 = \frac{5}{4} \times (x - 3) }\)
\( \implies \mathsf{(y - 2)4 = 5x - 15}\)
\( \implies \mathsf{4y - 8 = 5x - 15}\)
\( \implies \mathsf{(4y - 5x) - 8 + 15 = 0}\)
\( \implies \mathsf{4y - 5x + 7 = 0}\)
and thats the required equation of the perpendicular.
Is this correct or incorrect …..
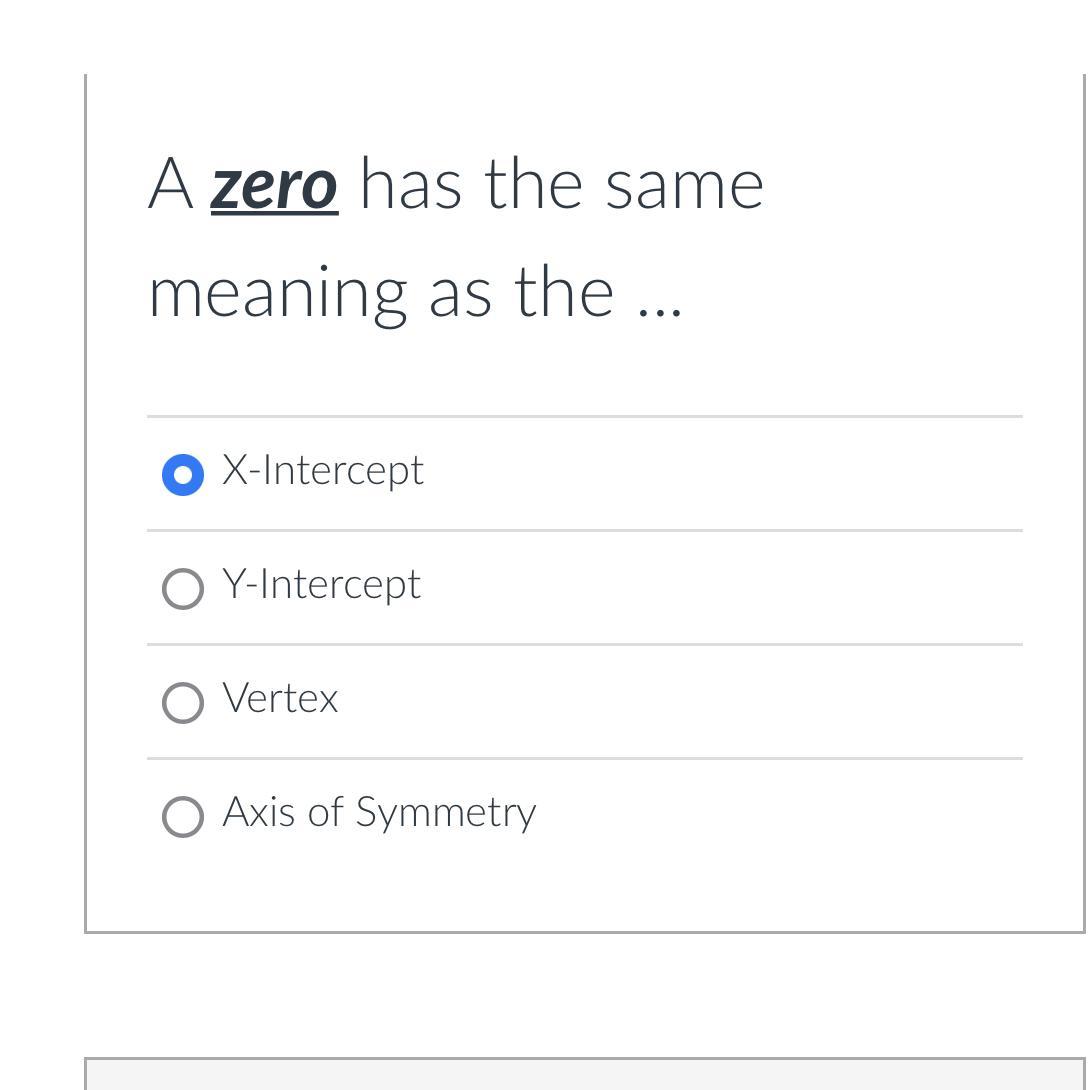
Answers
A zero has the same meaning as the vertex.
What is a vertex?The point where two lines meet forming an angle or set of angles is referred to as a vertex. This can also be called a point of origin especially when considering the axis of a Cartesian coordinate.
The vertex can be taken as zero since it is referred to as the point of origin. This is different to the axis of symmetry; as the axis of symmetry is one that splits a given plotted points i.e. a graph into two equal parts.
Thus, a zero has the same meaning as the vertex.
Learn more about vertex at https://brainly.com/question/1217219
#SPJ1
Find the distance between the Point C and Point D.
A. √49 units
B. √58 units
C. 10 units
D. √56 units
•C
3
2
ܘ ܐ ܐ
77
4977
D
3 4

Answers
The distance between point C (-3, 3) and point D (0, -4) is equal to: √58 units.
How to determine the distance between the coordinates for each points?In Mathematics and Geometry, the distance between two (2) end points that are on a coordinate plane can be calculated by using the following mathematical equation:
Distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
Where:
x and y represent the data points (coordinates) on a cartesian coordinate.
By substituting the given end points into the distance formula, we have the following;
Distance = √[(0 + 3)² + (-4 - 3)²]
Distance = √[(3)² + (-7)²]
Distance = √[9 + 49]
Distance = √58 units.
Read more on distance here: brainly.com/question/12470464
#SPJ1
which of the following is a number where the digit 2 represents 1/10 the value of the digit 2 in the number 1,947.5286
Answers
Answer:
0.002
Step-by-step explanation:
the digit "2" in this equation represents 0.02 or also 2/100
1/10 of 2/100 would be like multiplying 1/10 and 2/100 and that would get us 2/1000
2/1000 is also 0.002
0.002 is the value of the digit 2 in the number 1,947.5286.
What is number?A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words.
here we have,
the number 1,947.5286.
the digit "2" in this equation represents 0.02 or also 2/100
1/10 of 2/100 would be like multiplying 1/10 and 2/100
and that would get us 2/1000
i.e.
2/1000 is also 0.002
Hence, 0.002 is the value of the digit 2 in the number 1,947.5286.
To learn more on number click:
brainly.com/question/17429689
#SPJ2
A rocket is shot off from a launcher. The accompanying table represents the height of the rocket at given times, where x is time, in seconds, and y is height, in feet. Write a quadratic regression equation for this set of data, rounding all coefficients to the nearest hundredth. Using this equation, find the height, to the nearest foot, at a time of 5.1 seconds.
Time in Seconds (x) Height in Feet (y)
0.40.4 6464
0.80.8 122122
1.21.2 175175
1.61.6 223223
2.32.3 301301
Answers
Using a calculator, we find the quadratic regression equation, and find that the height at 5.1 seconds is of 879.57 feet.
How to find the equation of quadratic regression using a calculator?To find the equation, we need to insert the points (x,y) in the calculator.
In this problem, the points are given as follows:
(0.4, 64), (0.8, 122), (1.2, 175), (1.6, 223), (2.3, 301).
Inserting these points into a calculator, the equation is:
y = 3.47231343x² + 157.1327045x - 12.12067446.
The height at 5.1 seconds is of:
y = 3.47231343(5.1)² + 157.1327045(5.1) - 12.12067446.
y = 879.57.
More can be learned about regression equations at https://brainly.com/question/17261411
#SPJ1
Find the area of a square with perimeter 12 m.
Answers
Answer:
9 m²
Step-by-step explanation:
The perimeter of a square is 4x, where is the length of one side (because all the sides have the same length).
This means that 4x = 12, so x = 3, in other words the length of one side of the square is 3 m.
To work out the area of the square, multiply the length and the width together: 3 x 3 = 9 m²
Hope this helps!
Which choice is equivalent to the quotient shown here for acceptable values of X? A,B,C,D?

Answers
Answer: D
Step-by-step explanation: Cuz i just know
the probability that a student selected in our class will pass mathematics test is 2/3 how many students are likely to feel mathematics in the art class with 69 students
Answers
Out of 69 students in the art class, around 23 are expected to fail the mathematics test, assuming the probability of passing given is 2/3.
To determine how many students are likely to fail mathematics in the art class, we need to use the given probability of passing the mathematics test, which is 2/3.
First, let's find the probability of failing the mathematics test. Since passing and failing are complementary events (i.e., if the probability of passing is p, then the probability of failing is 1 - p), we can calculate the probability of failing as 1 - 2/3, which simplifies to 1/3.
Now, let's consider the art class, which has a total of 69 students. If the probability of failing mathematics is 1/3, then approximately 1/3 of the students in the art class are likely to fail the mathematics test.
To find the number of students likely to fail, we multiply the probability of failing (1/3) by the total number of students in the art class (69).
(1/3) * 69 ≈ 23
Therefore, approximately 23 students are likely to fail mathematics in the art class of 69 students based on the given probability of passing the mathematics test.
For more question on probability visit:
https://brainly.com/question/25839839
#SPJ8
What is the lcm of 84,102 and 100
Answers
Step-by-step explanation:
\(\sf{ 2 |{\underline{84,102,100}}}\)
\(\sf{ 2|{\underline{42,51,50}}}\)
\(\sf {3|{\underline{21,17,25}}}\)
\(\sf {5|{\underline{7,17,25}}}\)
\(\sf {\:\:{7,17,5}}\)
LCM=2×2×3×5×7×17=7120What is the average age of the porcupines at your zoo? What is the standard deviation? Round your answers to the nearest tenth.
Answers
Answer:
is there a pic?
Step-by-step explanation:
HELP WITH C
5mph buffer what is the new function and graph?

Answers
The function for fine at every speed should be doubled in construction zones is f(n)= -8.75n+637.5.
What is the function?Functions are the fundamental part of the calculus in mathematics. The functions are the special types of relations. A function in math is visualized as a rule, which gives a unique output for every input x.
The coordinate points from the graph are (10, 550) and (30, 200).
Here, slope = (200-550)(30-10)
= -350/20
= -35/2
= -17.5
Substitute m= -17.5 and (x, y)=(10, 550) in y=mx+c, we get
550=-17.5(10)+c
c=550+175
c=725
So, the equation is y= -17.5x+725
Thus, f(n)= -17.5n+725
a) The fine at every speed should go up by $10.
So, the coordinates are (10, 560) and (30, 210)
New slope (m)= (210-560)(30-10)
= -350/20
= -35/2
= -17.5
Substitute m= -17.5 and (x, y)=(10, 560) in y=mx+c, we get
560=-17.5(10)+c
c=550+175
c=735
So, the equation is y= -17.5x+735
Thus, f(n)= -17.5n+735
b) The fine at every speed should be doubled in construction zones.
So, the coordinates are (20, 550) and (60, 200)
New slope (m)= (200-550)(60-20)
= -350/40
= -8.75
Substitute m= -8.75 and (x, y)=(20, 550) in y=mx+c, we get
550=-8.75(10)+c
c=550+87.5
c=637.5
So, the equation is y= -8.75x+637.5
Thus, f(n)= -8.75n+637.5
Therefore, the function for fine at every speed should be doubled in construction zones is f(n)= -8.75n+637.5.
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ1

a family has two children. what is the probability that both are girls, given that at least one is a boy
Answers
Answer: The probability would be zero
Step-by-step explanation:
There are two children and one is a boy, so the probability of both being girls is a zero
if P = (4,2), Find: Rx=3 (P). Pls help!!

Answers
The coordinates of the reflected point P' will be (4, -3).
When a point is reflected over the x-axis, its y-coordinate changes sign.
In this case, the point P has coordinates (4,3).
To reflect it over the line x=3, we need to keep its x-coordinate the same and change its y-coordinate to its opposite.
So, the x-coordinate of the reflected point will still be 4, but the y-coordinate will become -3.
Therefore, the coordinates of the reflected point P will be (4, -3).
To learn more on Coordinate Geometry click:
brainly.com/question/27326241
#SPJ1
Answer:
Step-by-step explanation:
I’ll give brainliest

Answers
Step-by-step explanation:
Let
c = 11.5 cm
a = 8.9 cm
b = ?
Since this is a right triangle, we can use Pythagorean theorem to find the length of side b:
\(c^2 = a^2 + b^2\)
\(\Rightarrow b^2 = c^2 - a^2\)
Taking the square root of the equation above, we get
\(b = \sqrt{c^2 - a^2} = \sqrt{(11.5\:\text{cm})^2 - (8.9\:\text{cm})^2}\)
\(\:\:\:\:=7.3\:\text{cm}\)
One rectangle is "framed" within another. Find the area of the shaded region if the "frame" is 1 unit wide. 5 7
Answers
The area of the Shaded region, when the frame is 1 unit wide, is 20 square units.
The area of the shaded region when one rectangle is framed within another and the frame has a width of 1 unit, we need to calculate the difference between the areas of the outer rectangle and the inner rectangle.
the dimensions of the outer rectangle as length and width, and the dimensions of the inner rectangle as length' and width'. Based on the information provided, the length and width of the outer rectangle are 5 and 7 units, respectively.
The dimensions of the inner rectangle can be found by subtracting twice the width of the frame (1 unit) from the dimensions of the outer rectangle:
Length' = length - 2 * frame width = 5 - 2 * 1 = 3 units
Width' = width - 2 * frame width = 7 - 2 * 1 = 5 units
Now we can calculate the areas of the outer and inner rectangles:
Area of the outer rectangle = length * width = 5 * 7 = 35 square units
Area of the inner rectangle = length' * width' = 3 * 5 = 15 square units
Finally, to find the area of the shaded region, we subtract the area of the inner rectangle from the area of the outer rectangle:
Area of shaded region = Area of outer rectangle - Area of inner rectangle = 35 - 15 = 20 square units
Therefore, the area of the shaded region, when the frame is 1 unit wide, is 20 square units.
For more questions on Shaded region.
https://brainly.com/question/14989383
#SPJ8
find the 53th term in the following arithmetic sequence
2,9,16,23
Answers
Answer:
It's 366. 53*7=371 | 371-5 because the 0th term is -5
helpppppppp meeeeeee

Answers
Answer:
no ablo en inglés por q no soy loca
Simplify (x + 5)2 using the square of a binomial formula.
x² + 10x + 25
x²-10X-25
x²-10x+25
x² + 10x - 25
Answers
Answer:
\(x^2 + 10x + 25\)
Step-by-step explanation:
Hello!
Formula: \((a +b)^2 = a^2 + 2ab + b^2\)
a = xb = 5Plug it into the formula and simplify.
Simplify\((a +b)^2 = a^2 + 2ab + b^2\)\((x +5)^2 = x^2 + 2(x)(5) + 5^2\)\((x +5)^2 = x^2 + 10x + 25\)The answer is the first option: \(x^2 + 10x + 25\).
Answer:
x^2-10x+25
Step-by-step explanation:
This is the correct answer
Enter the number that belongs in the green box

Answers
Answer:
X=90
Step-by-step explanation:
The shape is a square and it has right angles which makes x=90
Answer:
90
Step-by-step explanation:
That middle part has to equal 360. Because its a square, we know that each on of those have to be 90
what is the value of (f-g)(2)

Answers
Answer:
Step-by-step explanation:
We need to find the value (f-g)(2), so we need first to substitute 2 into the given functions f(x) and g(x) and then subtract the result of g(2) from f(2).
Here, f(x) = 3x^2 + 1 and g(x) = 1 - x,
So, We will substitute 2 into these functions:
f(2) = 3(2)^2 + 1 = 3(4) + 1 = 12 + 1 = 13
g(2) = 1 - 2 = -1
Now, we can subtract g(2) from f(2):
(f-g)(2) = f(2) - g(2) = 13 - (-1) = 13 + 1 = 14
Hence, the required value of (f-g)(2) is 14.
Answer:
The correct answer is 3. To solve for g(-2), we substitute -2 for x in the equation g(x) = 2x + 5. This gives us g(-2) = 2(-2) + 5, which simplifies to -4 + 5 = 1. Next, we substitute the value of g(-2) into the equation for f(g(x)) = 4 - x^2. Thus, f(g(-2)) = 4 - (1)^2, which equals 4 - 1 = 3.
During the _________________ stage, kids develop the ability to take in other people’s perspective and begin to make cause-and-effect connections between events in their surroundings.
Answers
Answer:
Concrete Operational Stage or Perceptive thinking
Determining the area of a sector of a circle...

Answers
The area of a segment of a circle is (12π-9√3) square inches.
We have to determine the area of a segment of a circle.
The formula for the area of the sector that:
Arc length = πr² (θ/360)
Where r = the radius of the circle,
θ = the angle (in degrees) subtended by an arc at the center of the circle.
As per the shown figure, it is given that:
Central angle θ = 120°
The radius of a circle r = 6 in.
The area of the sector A₁ = π(6)² (120/360)
The area of the sector A₁ = 12π in²
The area of the triangle within the sector:
A₂ = 1/2 × (6√3)(3) = 9√3 in²
Now, the area of the segment is:
A₁ - A₂ = (12π - 9√3) in²
Therefore, the area of a segment of a circle is (12π-9√3) square inches.
Learn more about the arc of the circle here:
brainly.com/question/1577784
#SPJ1
Use properties to rewrite the given equation. Which equations have the same solution as 2.3p – 10.1 = 6.5p – 4 – 0.01p? Select two options. 2.3p – 10.1 = 6.4p – 4 2.3p – 10.1 = 6.49p – 4 230p – 1010 = 650p – 400 – p 23p – 101 = 65p – 40 – p 2.3p – 14.1 = 6.4p – 4
Answers
The equations that have the same solution are:
2.3p – 10.1 = 6.49p – 4
230p – 1010 = 650p – 400 – p
23p – 101 = 65p – 40 – p
Options B, C, and D are the correct answer.
What is a solution?Solutions are the values of an equation where the values are substituted in the variables of the equation and make the equality in the equation true.
We have,
2.3p - 10.1 = 6.5p - 4 - 0.01p
2.3p - 6.5p + 0.01p = 10.1 - 4
2.31p - 6.5p = 6.1
-4.19p = 6.1
p = -6.1/4.19
p = -1.5
Now,
Solve for p.
2.3p – 10.1 = 6.4p – 4
2.3p - 6.4p = 10.1 - 4
-4.1p - 6.4
p = -6.4/4.1
p = -1.6
2.3p – 10.1 = 6.49p – 4
2.3p - 6.49p = 10.1 - 4
-4.19p = 6.1
p = -1.5
230p – 1010 = 650p – 400 – p
230p - 649p = 1010 - 400
-419p = 610
p = -1.5
23p – 101 = 65p – 40 – p
23p - 64p = 101 - 40
-41p = 61
p = -1.5
2.3p – 14.1 = 6.4p – 4
2.3p - 6.4p = 14.1 - 4
-4.1p = 10.1
p = 2.5
Thus,
Equations that have the same solution
2.3p – 10.1 = 6.49p – 4
230p – 1010 = 650p – 400 – p
23p – 101 = 65p – 40 – p
Learn more about solutions of equations here:
https://brainly.com/question/545403
#SPJ1
is this graph a minimum or a maximum pls help

Answers
The vertex of the graph is a maximum at (-2, 4)
Calculating if the vertex of the graph a maximum or a minimum?From the question, we have the following parameters that can be used in our computation:
The graph
The graph is a quadratic function
From the graph, we can see that the graph has a maximum value
This maximum value represents the vertex of the graph
And it is located at (-2, 4)
So, we have
Maximum = (-2, 4)
Hence, the maximum value of the function is (-2, 4)
Read more about vertex at
brainly.com/question/28180581
#SPJ1
. Joaquin played basketball with his friends from 1:10 to 3:35. He arrived home 20 minutes later. How many minutes passed from the time Joaquin started playing basketball until the time he arrived at home?
Answers
Answer:
165 minutes
Step-by-step explanation:
To solve for the number of minutes that Joaquin played for, we can use this expression:
(let 'a' represent how much time passed from the time Joaquin started playing basketball until the time he arrived at home)
1:10 + a = 3:35Subtracting 1:10 from each side:
1:10 - 1:10 + a = 3:35 - 1:101:10 - 1:10 cancels out to 0, while 3:35 - 1:10 is equal to 2:25.
So, the expression is now:
a = 2:25So, 2 hours and 25 minutes passed.
If we know that 1 hour is equivalent to 60 minutes, we can use this expression to solve for however many minutes are in 2 hours:
2 × 60 = 120Now we need to add on the number of minutes and the time it took him to get home:
120 + 25 + 20 = 165Therefore, 165 minutes passed from the time Joaquin started playing basketball until the time he arrived at home.
write three different expressions that simplify to x^6
Answers
Three different expressions that simplify to x^6 are
x¹²/x⁶
x¹⁸/x¹²
x¹. x¹⁰/x⁵
What are index forms?Index forms are defined as mathematical expressions used to write numbers too small or large in more convenient forms.
Other names for index forms are standard forms and scientific notations.
Note some rules of indices, they are;
Subtract the exponents when dividing variables of the same basesAdd the exponents when multiplying variables of the same basesMultiply the exponents when expanding the bracket or parenthesesThen, we have;
x¹²/x⁶
x¹⁸/x¹²
x¹. x¹⁰/x⁵
Learn about index forms at: https://brainly.com/question/15361818
#SPJ1
Based on the values in the table below, find the slope and y-intercept to write the equation of the line in the form y=mx+b.
x= 1, 2, 3
y= 11, 22, 33
Answers
Answer:
y= 11x
Step-by-step explanation:
find the slope: 22-11/2-1= 11/1 or 11
To find the y-intercept you can use the slope by subtracting 11 (inverse operation) from the y value of (1,11). So the y- intercept is (0,0). To write the equation plug in 11 for m and 0 for b. Since 0 has no value the equation would be y= 11x
Please use the following for the next 6 questions. Suppose that the average weekly earnings for employees in general automotive repair shops is $450, and that the population standard deviation for the earnings for such employees is $50. A sample of 100 such employees is selected at random.
1) What is the probability distribution of the average weekly earnings for employees in general automotive repair shops?
2) Find the probability that the average weekly earnings is less than $445.
3) Find the probability that the average weekly earnings is exactly equal to $445.
4) Find the probability that the average weekly earnings is between $445 and $455.
5) In answering the previous 3 questions, did you have to make any assumptions about the population distribution?
6) Now assume that the weekly earnings for employees in all general automotive repair shops is normally distributed, obtain the probability that a given employee will earn more than $480 in a given week.
Answers
1) The probability distribution of the average weekly earnings for employees in general automotive repair shops is the sampling distribution of the sample mean. According to the Central Limit Theorem, if the sample size is large enough, the sampling distribution of the sample mean is approximately normal, with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.
2) To find the probability that the average weekly earnings is less than $445, we can standardize the sample mean and use a z-table. The z-score for $445 is calculated as follows: z = (445 - 450) / (50 / sqrt(100)) = -1. Using a z-table, we find that the probability that the average weekly earnings is less than $445 is approximately 0.1587.
3) Since we are dealing with a continuous distribution, the probability that the average weekly earnings is exactly equal to any specific value is zero.
4) To find the probability that the average weekly earnings is between $445 and $455, we can subtract the probability that it is less than $445 from the probability that it is less than $455. The z-score for $455 is calculated as follows: z = (455 - 450) / (50 / sqrt(100)) = 1. Using a z-table, we find that the probability that the average weekly earnings is less than $455 is approximately 0.8413. Therefore, the probability that it is between $445 and $455 is approximately 0.8413 - 0.1587 = 0.6826.
5) In answering questions 2-4, we made an assumption about the population distribution based on the Central Limit Theorem. We assumed that since our sample size was large enough (n=100), our sampling distribution would be approximately normal.
6) If we assume that weekly earnings for employees in all general automotive repair shops are normally distributed with a mean of $450 and a standard deviation of $50, then we can calculate the z-score for an employee earning more than $480 in a given week as follows: z = (480 - 450) / 50 = 0.6. Using a z-table, we find that the probability that an employee will earn more than $480 in a given week is approximately 1 - 0.7257 = 0.2743.
Add and Subtract Rational Expressions with a Common Denominator
In the following exercises, perform the indicated operations.

Answers
Answer:
\(\displaystyle \frac{4q^2-q+3}{q^2+6q+5}-\frac{3q^2-q-6}{q^2+6q+5}=\frac{q^2+9}{q^2+6q+5}\)
Step-by-step explanation:
Simplifying Rational Expressions
If two or more rational expressions have the same denominator, the add and subtract operations are done only with the numerator. The final denominator will be the common of both.
The expression is:
\(\displaystyle \frac{4q^2-q+3}{q^2+6q+5}-\frac{3q^2-q-6}{q^2+6q+5}\)
Operating on the numerators:
\(\displaystyle \frac{4q^2-q+3}{q^2+6q+5}-\frac{3q^2-q-6}{q^2+6q+5}=\frac{4q^2-q+3-(3q^2-q-6)}{q^2+6q+5}\)
Removing parentheses:
\(\displaystyle \frac{4q^2-q+3}{q^2+6q+5}-\frac{3q^2-q-6}{q^2+6q+5}=\frac{4q^2-q+3-3q^2+q+6}{q^2+6q+5}\)
Simplifying:
\(\boxed{\displaystyle \frac{4q^2-q+3}{q^2+6q+5}-\frac{3q^2-q-6}{q^2+6q+5}=\frac{q^2+9}{q^2+6q+5}}\)
The expression cannot be further simplified.