a box has width $m$, where $m$ is a prime number. if the box has height $m 2$, length $m-1$, and a volume of 140, what is $m$?
Answers
The width of the box m = 5 units
The width of the box = m units
Where m is a prime number
Height of the box = m+2 units
The length of the box = m -1 units
The volume of the box = 140 cubic units
The volume of the box = Length × width × height
140 = m × (m+2) × (m-1)
140 = (m^2 + 2m )(m-1)
140 = m^3 - m^2 + 2m^2 - 2m
140 = m^3 + m^2 - 2m
m^3 + m^2 - 2m - 140 = 0
We can split the equation by taking the common term outside
(m-5) (m^2 + 6m + 28) = 0
Therefore, one value of m = 5
5 is a prime number
Therefore, the value of m is 5
Learn more about volume here
brainly.com/question/13527107
#SPJ4
Related Questions
The function f(x) is translated left 3 units, down 2 units and is reflected across the x-axis to make the
new function g(x). Which of the following best represents g(x)
Answers
Answer:
2,3 is the paired fraction
Step-by-step explanation:
f ( x ) = 25 x 2 − 4
Answers
Answer:
the answer is to this question is f(x)=46
a) A circular channel section has diameter of 6m and it is running half. Calculate the discharge through the channel if the bed slope is 1 in 600 and manning’s co efficient is equal to 0.014.
Answers
To calculate the discharge through the circular channel, we can use Manning's equation, which relates the flow rate (Q) to the channel properties and flow conditions. Manning's equation is given by:
Q = (1/n) * A * R^(2/3) * S^(1/2)
where:
Q is the discharge (flow rate)
n is Manning's coefficient (0.014 in this case)
A is the cross-sectional area of the channel
R is the hydraulic radius of the channel
S is the slope of the channel bed
First, let's calculate the cross-sectional area (A) of the circular channel. The diameter of the channel is given as 6m, so the radius (r) is half of that, which is 3m. Therefore, the area can be calculated as:
A = π * r^2 = π * (3m)^2 = 9π m^2
Next, let's calculate the hydraulic radius (R) of the channel. For a circular channel, the hydraulic radius is equal to half of the diameter, which is:
R = r = 3m
Now, we can calculate the slope (S) of the channel bed. The given slope is 1 in 600, which means for every 600 units of horizontal distance, there is a 1-unit change in vertical distance. Therefore, the slope can be expressed as:
S = 1/600
Finally, we can substitute these values into Manning's equation to calculate the discharge (Q):
Q = (1/0.014) * (9π m^2) * (3m)^(2/3) * (1/600)^(1/2)
Using a calculator, the discharge can be evaluated to get the final result.
To learn more about coefficient : brainly.com/question/1594145
#SPJ11
Consider x=h(y,z) as a parametrized surface ?(y,z) in the natural way. Write the equation of the tangent plane to the surface at the point (?3,1,?2) [with the coefficient of x being 1] given that ?h?y (1,?2)=?3 and ?h?z (1,?2)=?5 .
Answers
The equation of the tangent plane to the surface x = h(y, z) at the point (-3, 1, -2) is: -3(x + 3) - 5(y - 1) + (z + 2) = 0.
To find the equation of the tangent plane to the parametrized surface x = h(y, z) at the point (x₀, y₀, z₀) = (-3, 1, -2) with the given partial derivatives, follow these steps:
Step 1: Calculate the gradient vector
Given that ∂h/∂y(1, -2) = -3 and ∂h/∂z(1, -2) = -5, the gradient vector of h at (1, -2) is:
∇h(1, -2) = <-3, -5>.
Step 2: Use the gradient vector to find the normal vector
The gradient vector represents the normal vector of the tangent plane:
Normal vector = <-3, -5, 1> (with the coefficient of x being 1, as required).
Step 3: Write the equation of the tangent plane using the point-normal form
The equation of the tangent plane in point-normal form is:
A(x - x₀) + B(y - y₀) + C(z - z₀) = 0,
where (A, B, C) is the normal vector and (x₀, y₀, z₀) is the point on the plane.
Plugging in the values, we get:
-3(x - (-3)) - 5(y - 1) + 1(z - (-2)) = 0.
So, the equation of the tangent plane to the surface x = h(y, z) at the point (-3, 1, -2) is:
-3(x + 3) - 5(y - 1) + (z + 2) = 0.
To know more about tangent plane visit:-
https://brainly.com/question/29730345
#SPJ11
Explain how the distance formula can prove Pythagoras' Theorem. In your
explanation use the Pythagoras Theorem and how the distance formula can be used
with a right triangle when only given the hypotenuse.
Answers
Answer:
Given a triangle ABC, Pythagoras' Theorem shows that:
\(c^2=a^2+b^2\)
Thus,
\(c = \sqrt{a^2+b^2}\)
The distance formula, gives an equivalent expression based on two points at the end of the hypotenuse for a triangle.
\(d^2 = (x_{2} -x_{1})^2 + (y_{2} -y_{1})^2\)
\(d = \sqrt{(x_{2}-x_{1})^2 + (y_{2} -y_{1})^2 }\)
Therefore when given the hypotenuse with endpoints at
\((x_{1}, y_{1}) and {(x_{2}, y_{2})\)
We know that the third point of the right triangle will be at
\((x_{2}, y_{1})\)
and that the two side lengths will be defined by the absolute values of:
\((x_{2} - x_{1}) = a\)
\((y_{2} - y_{1}) = b\)
Find the eigenvalues λn and eigenfunctions yn(x) for the given boundary-value problem. (Give your answers in terms of n, making sure that each value of n corresponds to a unique eigenvalue.) y'' + (λ + 1)y = 0, y'(0) = 0, y'(1) = 0
Answers
λn = (nπ)^2 - 1, and the corresponding eigenfunction is y_n(x) = B sin(nπ x).
How do we calculate?The general solution of the differential equation is of the form
y(x) = A sin(√(λ+1) x) + B cos(√(λ+1) x).
Applying the boundary condition y'(0) = 0, we have:
y'(x) = A√(λ+1) cos(√(λ+1) x) - B√(λ+1) sin(√(λ+1) x)
y'(0) = A√(λ+1) cos(0) - B√(λ+1) sin(0) = 0
Here A = 0.
Applying the boundary condition y'(1) = 0, we have:
y'(x) = - B√(λ+1) sin(√(λ+1) x)
y'(1) = - B√(λ+1) sin(√(λ+1)) = 0
Which means that √(λ+1) = nπ for n = 1, 2, 3, ...
In conclusiuon, λn = (nπ)^2 - 1, and the corresponding eigenfunction is y_n(x) = B sin(nπ x).
Learn more about eigenfunction at: https://brainly.com/question/2289152
#SPJ1
How can you prove the triangle sum theorem?
Answers
The sum of angle in a triangle is 180°
What is the sum of angle in a triangle?A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted \triangle ABC.
The sum of angle A, B and C is 180 i.e A+B +C = 180°
Also a triangle is a 3 sided polygon. The sum of of angle in a polygon is( n-2)180
How do we prove that the sum of angle in a triangle is 180°?
Since triangle is 3 sided, n= 3, because n denote the number if sides
therefore the sum of angle = (n-2) 180 = (3-2)×180
= 180°
therefore the sum of angle In a triangle is 180°
learn more about sum of angle In a triangle from
https://brainly.com/question/25215131
#SPJ1
what is the slope-intercept form of (-1, 3) and (-2, 3)
Answers
Answer: The answer is y=3.
Step-by-step explanation: Write in slope-intercept form, y=mx+b. Please mark me as brainliest.
In how many ways can 7 men and 7 women sit on a round table such that no two women sit together? (a) 2(7 !) (b) (6 !)2 (c) 7 ! × 6 ! (d) (7 !)
Answers
The total number of ways for the men and women to sit on the round table is d) 7!
Since the table is round, we can fix the position of any one person, say a man, without loss of generality. Then there are 7! ways to arrange the 7 men in the remaining positions around the table.
Now, we need to place the 7 women in such a way that no two of them sit together. This can be done as follows: We first place the 7 men in a row. Then, we place the 7 women in the 7 spaces between the men, such that no two women sit together.
The number of ways to do this is the same as the number of ways to arrange the 7 women in a line such that no two of them are consecutive. This is a classic example of a permutation problem with constraints, and the number of such arrangements is given by the formula:
P(7,7) - 7! = 7! - 7! = 6! x 7
Therefore, the total number of ways for the men and women to sit on the round table is:
7! x 6! x 7 = (7!)
For more questions like Permutation click the link below:
https://brainly.com/question/30649574
#SPJ11
.Show that {Y(t), t ≥ 0} is a Martingale when
Y(t) = B2(t) – t
What is E[Y(t)]?
Hint: First compute E[Y(t)|B(u), 0 ≤ u ≤ s].
Answers
To show that {Y(t), t ≥ 0} is a Martingale, we need to prove that E[Y(t)|F(s)] = Y(s) for all s ≤ t, where F(s) is the sigma-algebra generated by B(u), 0 ≤ u ≤ s.
Using the hint, we can compute E[Y(t)|F(s)] as follows:
E[Y(t)|F(s)] = E[B2(t) - t |F(s)]
= E[B2(t)|F(s)] - t (by linearity of conditional expectation)
= B2(s) - t (since B2(t) - t is a Martingale)
Therefore, we have shown that E[Y(t)|F(s)] = Y(s) for all s ≤ t, and thus {Y(t), t ≥ 0} is a Martingale.
To compute E[Y(t)], we can use the definition of a Martingale: E[Y(t)] = E[Y(0)] = E[B2(0)] - 0 = 0.
Learn more about Martingale here:
https://brainly.com/question/13679553
#SPJ11
We will show that {Y(t), t≥0} is a Martingale by computing its conditional expectation. The expected value of Y(t) is zero.
To show that {Y(t), t≥0} is a Martingale, we need to compute its conditional expectation given the information available up to time s, E[Y(t)|B(u), 0≤u≤s]. By the Martingale property, this conditional expectation should be equal to Y(s).
Using the fact that B2(t) - t is a Gaussian process with mean 0 and variance t3/3, we can compute the conditional expectation as follows:
E[Y(t)|B(u), 0≤u≤s] = E[B2(t) - t | B(u), 0≤u≤s]
= E[B2(s) + (B2(t) - B2(s)) - t | B(u), 0≤u≤s]
= B2(s) + E[B2(t) - B2(s) | B(u), 0≤u≤s] - t
= B2(s) + E[(B2(t) - B2(s))2 | B(u), 0≤u≤s] / (B2(t) - B2(s)) - t
= B2(s) + (t - s) - t
= B2(s) - s
Therefore, we have shown that E[Y(t)|B(u), 0≤u≤s] = Y(s), which implies that {Y(t), t≥0} is a Martingale.
Finally, we can compute the expected value of Y(t) as E[Y(t)] = E[B2(t) - t] = E[B2(t)] - t = t - t = 0, where we have used the fact that B2(t) is a Gaussian process with mean 0 and variance t2/2.
Learn more about variance here:
https://brainly.com/question/31432390
#SPJ11
The below data are for a hypothetical economy: (show your calculations) Number of employed = 480 million persons Not in the labour force = 125 million persons Number of Labour force = 625 million persons Using the above data, compute the following a. Number of unemployed, b. Unemployment-rate, c. Population
Answers
The number of unemployed in the given economy can be calculated as follows:
Unemployed = Number of Labour force - Number of Employed Unemployed = 625 million - 480 million Unemployed = 145 million
The unemployment rate can be calculated by dividing the number of unemployed individuals by the number of individuals in the labour force and then multiplying the quotient by 100.
Unemployment Rate = (Unemployed/Labour force) × 100 Unemployment Rate = (145 million/625 million) × 100 Unemployment Rate = 23.2%
The population of the given economy can be calculated as follows:
Population = Number of Employed + Number of Individuals not in Labour ForcePopulation = 480 million + 125 millionPopulation = 605 million
Therefore, the number of unemployed in the given economy is 145 million, the unemployment rate is 23.2%, and the population is 605 million.
To know more about hypothetical economy visit:
https://brainly.com/question/30889430
#SPJ11
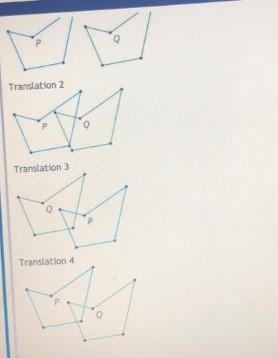
Match the directed line segment with the image of polygon P being transformed polygon Q by translation by the directed line segment
Answers
The directed line segment for all the given transformations to match the transformed line segment from translation 1 to translation 4.
How to Interpret Translation of line segments?In this question, the translations are defined by a line segment.
Such that in each translation, we can easily find the segment PQ (the measure and the direction).
And all the points in the Polygon P will be connected by that same segment PQ to the equivalent point in the Polygon Q. (where you only move the segment to the correct location, but the length and direction remains constant)
Thus, to find the line segment for each transformation, you need to correctly measure the length of the segment PQ, and also the direction (that can be defined by an angle).
With the above, we can find the directed line segment for all the given transformations to match the transformed line segment from translation 1 to translation 4.
Read more about line segments translation at; https://brainly.com/question/17370215
#SPJ1
Which graph best represents the linear function y = 3x -1

Answers
Answer:
c
Step-by-step explanation:
Demand for park visits is Q =10,000 −100P. How many visitors will attend if the park charges a $20.00 admission fee?
A. 2,000
B. 4,000
C. 6,000
D. 8,000
2. Suppose the demand for vanilla ice cream was described by the equation Q = 20 – p, and the supply was described by Q = 10 + p. What are the equilibrium price (P*) and quantity(Q*)?
A. P* = -40, Q* = 20
B. P* = 5, Q* = 15
C. P* = 10, Q* = 50
D. P* = 25, Q* = -25
Answers
1. The number of visitors attending the park when the admission fee is $20.00 is 8,000.
2. The equilibrium price (P*) is $5 and the equilibrium quantity (Q*) is 15.
1. To find the number of visitors attending the park when the admission fee is $20.00, we substitute P = $20.00 into the demand equation Q = 10,000 - 100P:
Q = 10,000 - 100(20)
Q = 10,000 - 2,000
Q = 8,000
Therefore, the number of visitors attending the park when the admission fee is $20.00 is 8,000. The correct answer is option D.
2. To find the equilibrium price (P*) and quantity (Q*) for vanilla ice cream, we set the demand equation equal to the supply equation and solve for P:
20 - p = 10 + p
Combine like terms:
2p = 10
Divide both sides by 2:
p = 5
To find the equilibrium quantity, substitute the value of p into either the demand or supply equation:
Q = 20 - p
Q = 20 - 5
Q = 15
Therefore, the equilibrium price (P*) is $5 and the equilibrium quantity (Q*) is 15. The correct answer is option B.
To learn more about equilibrium price
https://brainly.com/question/22569960
#SPJ11
for each ordered pair, determine whether it is a solution to the system of equations.
-3x+2y=5
2x-5y=4
(x, y)
(1,4)
(0, -7)
(-8, -4)
(-3, -2)
Which one(s) are a solution?
Answers
The coordinates of the vertices of a triangle
are P(2,3), R(4, 5), and S(6,3). The
triangle PRS is reflected across the x-axis
to create triangle P'R'S. Which rule
describes this transformation?
A. (x, y)--(-x, -y)
B. (x, y)--(-x, y)
C. (x, y) --(x, -y)
D. (x,y) --(x,y)
Answers
Answer:
B?
Step-by-step explanation:
What is 32.8 divided 5.
Answers
Answer:
Step-by-step explanation:
6.56
Question 2:
The Project Manager found that distribution of the amount of gravel (in tons) sold by a particular construction supply company in a given week is a continuous random variable X with PDF as
3(1−x2) 0≤x ≤1 (x) = {2
0 h
a) Find the expected value and standard deviation of the amount of gravel sold in a week.
Consider a normally distributed random variable X with a mean of 85 and standard deviation of 10. Find P(90≤X≤100)?
Answers
a) To find the expected value (mean) of the amount of gravel sold in a week, we need to calculate the integral of x times the probability density function (PDF) over the interval [0, 1].
The expected value is given by:
E[X] = ∫x * f(x) dx
Integrating the given PDF over the interval [0, 1]:
E[X] = ∫x * 3(1 - x^2) dx
= 3∫(x - x^3) dx
= 3[(x^2/2) - (x^4/4)] evaluated from 0 to 1
= 3[(1/2) - (1/4) - (0 - 0)]
= 3(1/4)
= 3/4
= 0.75
Therefore, the expected value of the amount of gravel sold in a week is 0.75 tons.
To find the standard deviation, we need to calculate the variance first.
The variance is given by:
Var(X) = E[X^2] - (E[X])^2
To calculate E[X^2], we integrate x^2 times the PDF over the interval [0, 1]:
E[X^2] = ∫x^2 * 3(1 - x^2) dx
= 3∫(x^2 - x^4) dx
= 3[(x^3/3) - (x^5/5)] evaluated from 0 to 1
= 3[(1/3) - (1/5) - (0 - 0)]
= 3(8/15)
= 8/5
= 1.6
Substituting the values into the variance formula:
Var(X) = 1.6 - (0.75)^2
= 1.6 - 0.5625
= 1.0375
Finally, the standard deviation is the square root of the variance:
σ = √(Var(X))
= √(1.0375)
≈ 1.018
Therefore, the standard deviation of the amount of gravel sold in a week is approximately 1.018 tons.
b) To find P(90 ≤ X ≤ 100) for a normally distributed random variable X with a mean (μ) of 85 and a standard deviation (σ) of 10, we need to calculate the probability using the standard normal distribution.
First, we standardize the values:
z1 = (90 - 85) / 10
= 0.5
z2 = (100 - 85) / 10
= 1.5
Next, we look up the corresponding probabilities from the standard normal distribution table:
P(0 ≤ Z ≤ 0.5) = 0.3085
P(0 ≤ Z ≤ 1.5) = 0.4332
Finally, we calculate the desired probability using the properties of the standard normal distribution:
P(90 ≤ X ≤ 100) = P(0 ≤ Z ≤ 1.5) - P(0 ≤ Z ≤ 0.5)
= 0.4332 - 0.3085
= 0.1247
Therefore, the probability of 90 ≤ X ≤ 100 for a normally distributed random variable X with a mean of 85 and a standard deviation of 10 is approximately 0.1247.
Learn more about integral here
https://brainly.com/question/22008756
#SPJ11
9x + 3y = -15
-18x - 6y = 30
X = ?
Y = ?
Answers
Answer:
x = x, y = −5 −3x
Step-by-step explanation:
hope this helps
what does correlation investigate? select one: a. linear association between two numeric variables b. variances between two numeric variables c. association between two categorical variables d. differences of means between two numeric variables
Answers
Correlation is a bi-variate analysis that measures the strength of association between two variables and the direction of the relationship.
What is bi-variate analysis?
Bivariate analysis is one in every of the only kinds of quantitative (statistical) analysis. It involves the analysis of 2 variables (often denoted as X, Y), for the aim of deciding the empirical relationship between them.
Main Body:
The correlation coefficient's value ranges from +1 to -1. the entire degree of correlation between the 2 variables is indicated by a worth of one. The association between the 2 variables are weaker because the parametric statistic price approaches zero.
Hence correlation investigate linear association between two variables.
To know more about bi-variate analysis click on the link below
https://brainly.com/question/16795255
#SPJ4
PLEASE HELP whoever answers all of them and first i’m giving brainliest.

Answers
Answer:
1. To solve a one-variable equation, it may be necessary to first multiply by using the Distributive Property
2. The next step is to combine like terms as needed.
3. Then solve for the variable by applying inverse operations.
4. If solving lead to a true equation, then the equation has infinitely many solutions.
5. if solving leads to an untrue equation, then the equation has no solution.
what is 55+55 fassttt!!!!!!!!!
Answers
8 7/90 in decimal form
Answers
Answer:
0.07–
Step-by-step explanation:
The answer is above :)
Answer:
to express in decimal form , we have to join convert the mixed fraction into a improper fraction.
8 7/90 = d * w + n
= 90 * 8 + 7
= 720 + 7
= 727 / 90
now you have to make the denominator into a mutiple of 10
= 727 / 90 divided by 9
= 80 / 10
= 0.80
Step-by-step explanation:
hope it helps .
Which of the following is not a correct description of the graph of the function (photo below)

Answers
Answer:
the answer is d
Step-by-step explanation:
hope this helps
Hi can someone thoughrly answer the question below for brainliest please

Answers
The minimum number of neckless needed to sell to make a profit is 18 thus option (A) is correct.
What is inequality?A difference between two values indicates whether one is smaller, larger, or basically not similar to the other.
In other words, inequality is just the opposite of equality for example 2 =2 then it is equal but if I say 3 =6 then it is wrong the correct expression is 3 < 6.
As per the given,
12n > 135 + 4.50n
In order to make a profit and solve inequality,
12n - 4.50n > 135
7.5n > 135
n > 18
Thus, it needed to sell more than 18 to make a profit.
Hence "The bare minimum of necklaces that must be sold in order to turn a profit is 18".
For more about inequality,
brainly.com/question/20383699
#SPJ1
using complete sentences, compare the range values of the data sets. what does this comparison tell you in terms of the situation the data represent?
Answers
The scores of both groups are skewed, so the median and standard deviation are the best measures for comparison. Option D is correct.
In comparing the test scores of two groups, it is important to choose appropriate measures of center and variation to accurately represent the data. If both distributions are nearly symmetric, the mean and standard deviation are commonly used.
However, if the distributions are skewed, it is better to use the median and standard deviation as measures. In this particular case, the scores of Group B are skewed right, which means that the mean may not be a reliable measure of center. Instead, the median should be used. The range is not a good measure of variation for skewed data because it is sensitive to extreme values, so the standard deviation is more appropriate. Hence, option D is answer.
To know more about distributions, here
brainly.com/question/13955188
#SPJ4
--The complete question is, The table shows the test scores of students who studied for a test as a group (Group A) and students who studied individually (Group B).
Which would be the best measures of center and variation to use to compare the data?
The scores of Group B are skewed right, so the mean and range are the best measures for comparison.
Both distributions are nearly symmetric, so the mean and the standard deviation are the best measures for comparison.
Both distributions are nearly symmetric, so the median and the interquartile range are the best measures for comparison.
The scores of both groups are skewed, so the median and standard deviation are the best measures for comparison.--

the ratio of two supplementary angles is 3:9 what is the measure of the larger angle
Answers
Answer:
135
Step-by-step explanation:
Ratio = 3 : 9
Angles are : 3x , 9x
3x + 9x = 180 {supplementary angles}
12x = 180 {divide both side by 12}
x = 180/12
x = 15
Larger angle = 9x = 9*15 = 135
A merchant bought an item for $50.00 and sold it for 30% more. For what price did the merchant sell the item?
Answers
If a merchant bought an item for $50.00 and sold it for 30% more (markup), the item's selling price was $65.00.
What is the markup?The markup is the percentage or amount by which an item is sold.
The markup is based on the cost price. After adding the markup amount, the selling price is determined to generate some profits for the seller.
The purchase price of an item = $50.00
The markup = 30%
Markup factor = 1.3 (1 + 0.3)
The selling price of the item = $65.00 ($50.00 x 1.3)
Thus, for adding 30% more (markup) on the cost of the item, the selling price is determined as $65.00.
Learn more about markups at https://brainly.com/question/1445853.
#SPJ1
What is the factored form of the expression 5p^3-10p^2+3p-6
Answers
Answer: (5p^2+3)(p-2)
Step-by-step explanation:
In this problem, we need to write the factor form of expression .
5p^3-10p^2+3p-6
It can be done as follows :
5p^3-10p^2+3p-6=(5p^3+3p)+(-10p^2-6)
Taking common form the terms as follows :
=p(5p^2+3)-2(5p^2+3)
It can be also written as :
=(5p^2 +3)(p-2)
Hence, the factored form of is
Answer:
(p-2)(5p^2+3)
Step-by-step explanation:
see the image

What is the circumference of the circle? Use 3.14 pi
Answers
Answer: multiply the diameter of the circle with π (pi). The circumference can also be calculated by multiplying 2×radius with pi (π=3.14)
Step-by-step explanation:
becaue... multiply the diameter of the circle with π (pi). The circumference can also be calculated by multiplying 2×radius with pi (π=3.14)