A coffee connoisseur claims that he can distinguish between a cup of instant coffee and a cup of percolator coffee 75% of the time. It is agreed that his claim will be accepted if he correctly identifies at least 5 of the 6 cups. Find his chances of having the claims i) Accepted ii) rejected, when he does have ability he claims. (10) Q. No 4 (20 Marks; CLO-02,) a) To avoid detection at customs, a traveler places 6 narcotic tablets in a bottle containing 9 vitamin tablets that are similar in appearance. If the customs official selects 3 of the tablets at random for analysis, what is the probability that (10) the traveler will be arrested for illegal possession of narcotics?
Answers
The coffee connoisseur claims that he can distinguish between a cup of instant coffee and a cup of percolator coffee 75% of the time.
It is agreed that his claim will be accepted if he correctly identifies at least 5 of the 6 cups.In this case, the total number of ways of selecting 6 cups from a total of 6 cups is 6C6 = 1. There is only one possibility.There are 6 ways to choose 5 of the 6 cups, and there are 6 ways to pick any one of the 6 cups to be incorrect. Therefore, there are 6 × 6 = 36 different ways to choose five cups correctly and one cup incorrectly.
There are 6 ways to select all 6 cups correctly. This is the only possibility.Therefore, the total number of ways that the claims will be accepted is 36 + 1 = 37.The total number of ways that the claims will be rejected is equal to the number of ways that 4 or fewer cups will be correctly identified.There are 6 ways to select no cups correctly. There are 6 ways to pick any one of the 6 cups to be correct and miss all the others. There are 6C2 = 15 ways to select exactly two cups correctly and four cups incorrectly.
To know more about percolator visit:
https://brainly.com/question/31763172
#SPJ11
Related Questions
The graph of a proportional relationship passes through the point (6, 21). What is the equation for the relationship?
Answers
Answer:
The equation for the relationship is \(y = \frac{7}{2}\cdot x\).
Step-by-step explanation:
Given that point \((x,y) = (6, 21)\) is part of a direct relationship. That is:
\(y \propto x\)
\(y = k\cdot x\) (1)
Where \(k\) is the proportionality constant.
If we know that \(x = 6\) and \(y = 21\), then the proportionality constant is:
\(k = \frac{y}{x}\)
\(k = \frac{21}{6}\)
\(k = \frac{7}{2}\)
Lastly, the equation for the relationship is \(y = \frac{7}{2}\cdot x\).
Which of these is the algebraic expression for the verbal expression "ten times the difference of a number and twelve?" can someone tell me the answer plus i cann't even log in
Answers
Answer:
10(x - 12)
Step-by-step explanation:
10(x - 12)
10x - 120 Distributive Property
The recreation department is creating teams for baseball. 295 people have signed up. How many teams of 24 people will they be able to make? Will there be anyone left over?
Answers
Answer:
There will be 12 full teams and 7 extra people.
Step-by-step explanation:
Please mark me Brainliest
Solve the following word problems using your knowledge of trigonometry: 3. A rope is stretched from the top of a vertical pole to a point 10.5 m from the bottom of the pole.The rope makes an angle of 28'with the pole.How tall is the pole?
Answers
The height of the pole is approximately 5.59 meters.
To solve the word problem using trigonometry, we can use the tangent function. Let's denote the height of the pole as h.
We have a right triangle formed by the height of the pole, the distance from the bottom of the pole to the point where the rope is stretched, and the rope itself. The angle between the pole and the rope is given as 28 degrees.
Using the tangent function, we can set up the following equation:
tan(28 degrees) = h / 10.5 m
To find the value of h, we can rearrange the equation:
h = 10.5 m * tan(28 degrees)
Using a calculator, we can find the value of tan(28 degrees) ≈ 0.5317. Substituting this value into the equation, we get:
h = 10.5 m * 0.5317
h ≈ 5.59 m (rounded to two decimal places)
Learn more about height here:-
https://brainly.com/question/29131380
#SPJ11
Find the minimum, maximum, and range for the given set of data.
{23.5, 22.1, 24.0, 28.6, 26.3, 29.2, 21.0, 22.7, 25.5, 22.3, 21.6}
A.
minimum = 21.0, maximum = 29.2, range = 50.2
B.
minimum = 21.0, maximum = 29.2, range = 8.2
C.
minimum = 22.1, maximum = 26.3, range = 48.4
D.
minimum = 22.1, maximum = 26.3, range = 4.2
Answers
Answer:B
Step-by-step explanation:
need HELP ON THIS A S AP !!!!!

Answers
Answer:
803.84yd²
Step-by-step explanation:
Surface Area of A Sphere: \(A=4\pi r^2\)
We are given the radius of 8 yards.
Using 3.14 for pi:
\(A=4*3.14*8^2\\\\A=4*3.14*64\\\\A=12.56*64\\\\\boxed{A=803.84}\)
The correct answer should be 803.84yd².
Brainilest Appreciated.
Answer:
803.84 yd^2
Step-by-step explanation:
4*3.14*8^2
12.56*64
803.84
brainliest pls
hope i helped
-ZYLYNN
Find the area under the given curve over the interval. \( y=e^{x},[0,4] \)
Answers
The area under the curve y = eˣ over the interval [0,4] is e⁴-1
To find the area under the curve of
y = eˣ over the interval [0, 4], we use the definite integral.
Write the integral expression:
∫₀⁴ eˣ dx.
Integrate eˣ with respect to x. The antiderivative of eˣ is eˣ.
Evaluate the antiderivative at the upper and lower limits of integration:
[eˣ]₀⁴ = e⁴ - e⁰ .
Simplify the expression:
e⁴ - e⁰ = e⁴ - 1 .
Thus, the area under the curve of y = eˣ over the interval [0, 4] is e⁴ - 1 , which is approximately 53.598. This represents the total area enclosed by the curve y = eˣ and the x-axis between x = 0 and x = 4. The exponential function eˣ grows rapidly, resulting in a substantial area under the curve in this interval.
To know more about definite integral, visit:
https://brainly.com/question/31876258
#SPJ11
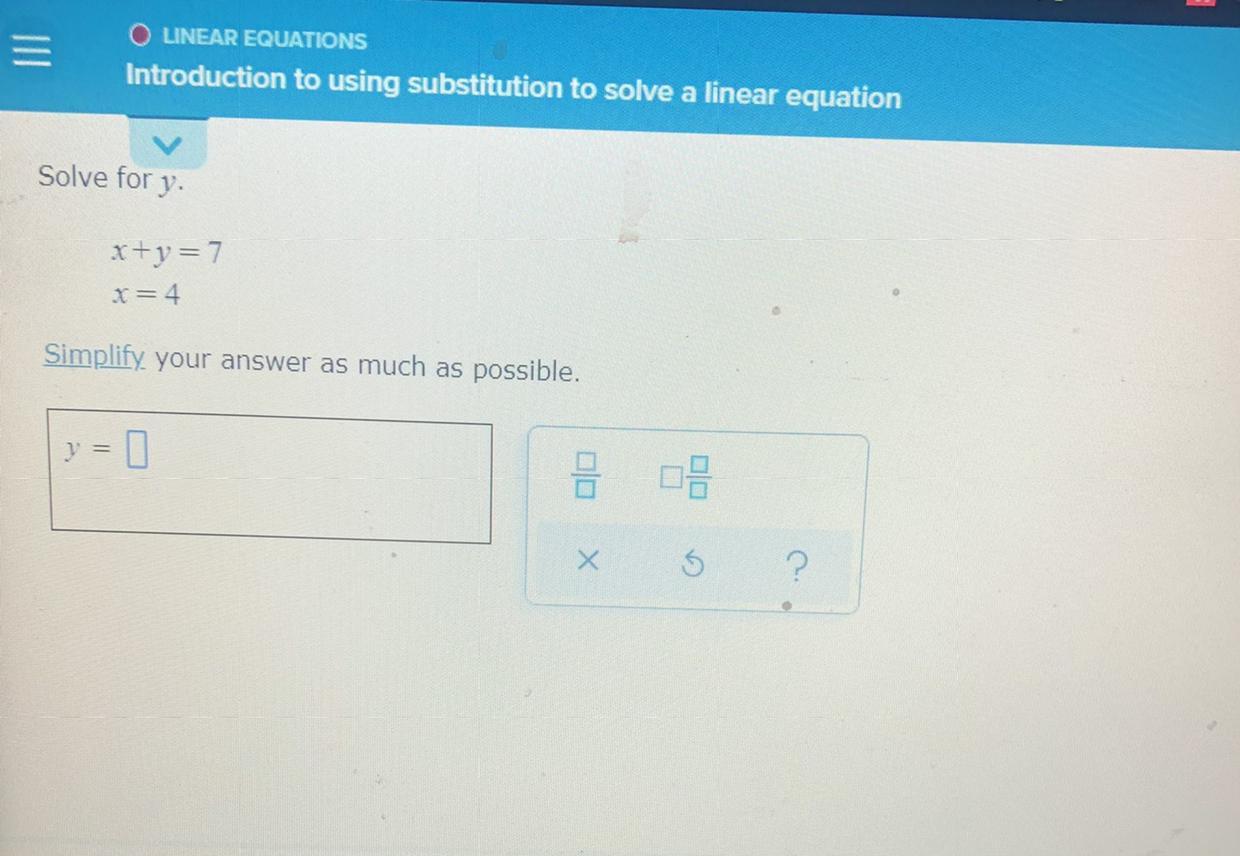
Please help with this question!!
Answers
The value of y is 3 if the value of x is 4 in the linear equation with two variables.
What is a linear equation?It is defined as the relation between two variables, if we plot the graph of the linear equation we will get a straight line.
If in the linear equation, one variable is present, then the equation is known as the linear equation in one variable.
We have:
Two linear equations in two variables x and y
x + y = 7
x = 4
Plug x = 4 in the equation x + y = 7, we get:
4 + y = 7
y = 7 - 4
y = 3
Thus, the value of y is 3 if the value of x is 4 in the linear equation with two variables.
Learn more about the linear equation here:
brainly.com/question/11897796
#SPJ1
Answer:
The value of y is 3 if the value of x is 4 in the linear equation with two variables.
What is a linear equation?
It is defined as the relation between two variables, if we plot the graph of the linear equation we will get a straight line.
If in the linear equation, one variable is present, then the equation is known as the linear equation in one variable.
We have:
Two linear equations in two variables x and y
x + y = 7
x = 4
Plug x = 4 in the equation x + y = 7, we get:
4 + y = 7
y = 7 - 4
y = 3
Step-by-step explanation:
Who do you think killed Jody Woah??
Answers
Answer:
who is he?
Step-by-step explanation:
A. 3/5
B. -3/5
C. -5/3
D. 5/3

Answers
Answer:
your answer would be A I think
Answer:
i did not understand but i think its
-3/5 i'm not sureeeeeeeee
Step-by-step explanation:
a recipe for sparking grape juice for 1 1/2 quarts of sparkling water and 2/4 quart grape juice Q1 How much sparkling water would you need to mix with 9 quarts of grape juice Q2 HOw much grape juice would you need to mix with 15/4 quarts of sparkling water Q3 How much of each ingredient would you need to make 100 quarts of punch
Answers
The quarts of water needed for 9 quarts of grape juice is 18 quarts of water .
The amount of grape juice needed for 15 / 4 quarts of water is 1 7/8.
The amount of water needed for 100 quarts is 66 2/3 quarts.
The amount of grape juice needed for 100 quarts is 33 1/3 quarts.
How much grape juice and sparkling water is needed?The first step is to determine the ratio between the ingredients needed for sparking grape juice.
Ratio of sparking water to grape juice - 1 1/2 : 2/4
When expressed in its simplest form, the ratio becomes - 1 1/2 : 1.2
This means that there are twice the amount of water is needed for 1 quart of grape juice.
Quarts of sparking water needed for 9 quarts of grape juice = 9 x 2 = 18 quarts of sparking water
Grape juice needed for 15/4 quarts of sparking water = 15 / 4 ÷ 2
15 / 4 x 1/2 = 15 / 8 = 1 7/8
Let a represent the quarts of grape juice that would be used to make 100 quarts of punch.
Let a represent the quarts of sparking water that would be used to make 100 quarts of punch.
a + 2a = 100
3a = 100
a = 100 / 3
a = 33 1/3
Quarts of sparking water needed = 100 - 331/3 = 66 2/3 quarts
To learn more about mixtures, please check: https://brainly.com/question/11729084
#SPJ1
Determine whether the probabilities below are computed using the classical method, empirical method, or subjective method.
The probability of having six girls in an six-child family is 0.015625.
A.Empirical method
B.Classical method
C.Subjective method
D.It is impossible to determine which method is used.
Answers
The given probability of having six girls in a six-child family is 0.015625. To determine the method used to compute this probability, we need to analyze the information provided.
The Classical method is based on theoretical assumptions and probabilities calculated using mathematical principles. It assumes equally likely outcomes and relies on counting favorable outcomes over the total number of possible outcomes.
The Empirical method involves gathering data from observations or experiments to estimate probabilities. It relies on observed frequencies and relative frequencies to compute probabilities. However, the given probability does not suggest a sample or data collection, making it unlikely that the Empirical method was used.
The Subjective method involves assigning probabilities based on personal judgment or opinions. Individuals subjectively evaluate the likelihood of an event based on their own beliefs or knowledge.
To learn more about probability : brainly.com/question/31828911
#SPJ11
Explain WHAT WOULD HAPPEN TO motion IF friction DID NDT EXIST.
Answers
Answer:
If friction did not exist, it would be hard for us to slow down in running, or putting breaks on a car, and more!
If friction did not exist, your car will slide down the road even if you try your best to put the brakes on a car. Friction is a very important force to slow down things that are moving very fast
Step-by-step explanation:
Hoped this helped.
\(GeniusUser\)
what is 42 x 2 give the working please help
Answers
Answer:
84.
Step-by-step explanation:
42
x 2
84
2 x 2 = 4
4 x 2 = 8
= 84
Answer:
Technically, 42×2=84
Step-by-step explanation:
You could do this by adding 42+42=84
Multiplying 2 times the 2 and the 4, which gives you 84.
If you wanted the factoring then:
2 is a prime number
42 could be like 42
/ \
21 2
/ \
7 3
but I dont really know how factoring would help you multiply. I hope this helps
-3 2a-²63 (a) Simplify and express your answer with positive indices. 3ab² (b) Fully simplify the following: 42²-9 i) X 10x² +13r-3 a-¹-6-¹ a-¹ + b-¹ ii) (5x - 1)² 10x²17r+3 (c) The total resistance of an electrical circuit (R), is given by the following formula if the resistors are connected in parallel. 1 1 1 1 + + R R₁ R₂ R₁ i) Express R₂ in terms of R, R, and R. [2] ii) Find the value of R₂ if R=1.50, R₁ = 502 and Rs = 30. (d) The velocity v of a particle is given as v²=u²+2as, where u is the initial velocity, a is the acceleration, and s is the travelled distance. Calculates in metres when u=6 ms ¹, v= 10 ms and a 2 ms-² (21 (e) If I paid $1.45 for an apple and an orange, and the apple cost 15 cents more than the orange, how much did the orange cost? [21 [¹] E
Answers
The correct answer is the orange costs $0.65.
(a) Simplify and express your answer with positive indices:
To simplify \(-3a^(-2) / 63\), we can rewrite it as \((-3/63) * a^(-2).\)
Simplifying -3/63 gives us -1/21.
Therefore, the simplified expression is (-1/21) * a^(-2), or -a^(-2) / 21.
(b) Fully simplify the following expression:
\(42^2 - 9 / (10x^2 + 13r^(-3)) * a^(-1) - 6^(-1) * a^(-1) + b^(-1)\)
To simplify this expression, we can start by evaluating the powers and performing the calculations:
\(42^2 = 1764\)
\(9 / (10x^2 + 13r^(-3)) = 9 / (10x^2 + 1/(13r^3)) = 9 / (10x^2 + 1/13r^3)\)
Next, we can simplify the terms involving exponents:
\(a^(-1) - 6^(-1) = 1/a - 1/6\)
\(a^(-1) + b^(-1) = 1/a + 1/b\)
Putting it all together, the fully simplified expression is:
\(1764 - 9 / (10x^2 + 1/13r^3) * (1/a - 1/6) + 1/a + 1/b\)
(c) The total resistance of an electrical circuit (R) when the resistors are connected in parallel is given by the formula:
1/R = 1/R₁ + 1/R₂
i) Express R₂ in terms of R, R₁, and R:To express R₂ in terms of R, R₁, and R, we can rearrange the formula:
1/R₂ = 1/R - 1/R₁
Taking the reciprocal of both sides:
R₂ = 1 / (1/R - 1/R₁)ii) Find the value of R₂ if R = 1.50, R₁ = 502, and Rs = 30:
Substituting the given values into the expression for R₂:
R₂ = 1 / (1/1.50 - 1/502)
= 1 / (2/3 - 1/502)
= 1 / (1004/1506 - 3/502)
= 1 / (1004/1506 - 9/1506)
= 1 / (995/1506)
= 1506 / 995
Therefore, the value of R₂ is approximately 1.5146.
(d) The velocity v of a particle is given by the equation v² = u² + 2as, where u is the initial velocity, a is the acceleration, and s is the traveled distance.
Given: u = 6 m/s, v = 10 m/s, and a = 2 m/s^(-2)
We can substitute the given values into the equation and solve for s:
v² = u² + 2as
\((10)^2 = (6)^2 + 2 * 2 * s\)
100 = 36 + 4s
4s = 100 - 36
4s = 64
s = 64 / 4
s = 16
Therefore, when u = 6 m/s, v = 10 m/s, and a = 2 m/s^(-2), the traveled distance s is 16 meters.(e) If you paid $1.45 for an apple and an orange, and the apple cost 15 cents more than the orange, we can set up the following equation:
apple + orange = $1.45apple = orange + $0.15
Substituting the second equation into the first equation:
(orange + $0.15) + orange = $1.45
2 * orange + $0.15 = $1.45
2 * orange = $1.45 - $0.15
2 * orange = $1.30
orange = $1.30 / 2
Therefore, the orange costs $0.65.
Learn more about function equations here:
https://brainly.com/question/11624077
#SPJ11
5 ex to the power of 2. minus 36 ex. + 36. = 0
Answers
Answer:
The answer is x=6
Please help! (Also show work)
Tutorials :D

Answers
The five-number summary is:
Minimum: 9
First Quartile: 16.5
Median: 25.5
Third Quartile: 39
Maximum: 51
3. Range = 42
4. Interquartile range = 22.5
How to Find the Five-number Summary of a Data?Given the data for the lengths as, 36, 15, 9, 22, 36, 14, 42, 45, 51, 29, 18, 20, to find the five-number summary of the data set, we would follow the steps below:
1. The numbers in ordered from the smallest to the largest would be:
9, 14, 15, 18, 20, 22, 29, 36, 36, 42, 45, 51
2. The five-number summary for the lengths in minutes would be:
Minimum value: this is the smallest lengths, which is 9First Quartile (Q1): this is the middle of the first half of the data set of the lengths in minutes, which is 16.5.Median: the median is the center of the data distribution which is 25.5.Third Quartile: this is the middle of the second half of the data set of the lengths in minutes, which is 39.Maximum: this is the largest length in minutes, which is, 51.3. Range of the data = max - min = 51 - 9 = 42
4. The interquartile range for the data set = Q3 - Q1 = 39 - 16.5
Interquartile range for the data set = 22.5
Learn more about the five-number summary on:
https://brainly.com/question/24809873
#SPJ1
Consider a continuous random variable x, which is uniformly distributed between 65 and 85. The probability of x taking on a value between 75 to 90 is ________. 0.50 0.075 0.75 1.00
Answers
The probability of x taking on a value between 75 to 90 is 0.25.
Given that x is a continuous random variable uniformly distributed between 65 and 85.To find the probability that x lies between 75 and 90, we need to find the area under the curve between the values 75 and 85, and add to that the area under the curve between 85 and 90.
The curve represents a rectangular shape, the height of which is the maximum probability. So, the height is given by the formula height of the curve = 1/ (b-a) = 1/ (85-65) = 1/20.Area under the curve between 75 and 85 is = (85-75) * (1/20) = (10/20) = 0.5Area under the curve between 85 and 90 is = (90-85) * (1/20) = (5/20) = 0.25.
To know more about variable visit:
https://brainly.com/question/15740935
#SPJ11
PLS HELP
what is the slope of the line that contains these points
x 15,17,19,21
————————-
y -10,2,14,26
Answers
Answer:
6
Step-by-step explanation:
(15 , -10) (17 , 2)
slope (m) = rise/run = (2 - -10) / (17 - 15) = 12/2 = 6
2-(-10), or 2+10 since you’re subtracting a negative and they cancel out is equal to 12. Now take your two x points, 15 and 17. 17-15 is equal to 2. Take 12 and divide it by the 2, which is then 6. Hope this helps.
a web music store offers two versions of a popular song. the size of the standard version is 2.4 megabytes (mb). the size of the high-quality version is 4.7 mb. yesterday, there were 720 downloads of the song, for a total download size of 2349 mb. how many downloads of the standard version were there?
Answers
By applying substitution method, it can be concluded that there were 350 downloaded standard versions.
Two-variable linear equations system is a mathematical equation consisting of two linear equations, each of which has two variables, for example, variable x and variable y.
Substitution method is a method to solve a two-variable linear equations system by changing one variable with a variable from another equation.
Information obtained from the problem:
Size of standard version = 2.4 megabytes
Size of high-quality version = 4.7 megabytes
Total downloads = 720 downloads
Total download size = 2349 megabytes
Let's assume the number of standard version downloads is S and the high-quality download is H, then we obtain the following equations:
S + H = 720 ......................... (1)
2.4S + 4.7H = 2349 ............(2)
To solve these equations, first, we have to determine the value of one of the variables using the first equation. Let's pick S.
S = 720 - H
Then we can substitute the value of S into the second equation:
2.4S + 4.7H = 2349
2.4(720 - H) + 4.7H = 2349
1728 - 2.4H + 4.7H = 2349
2.3H = 621
H = 270
As we know the value of H, we can calculate S:
S = 720 - H
= 720 - 270
= 450
Thus, there were 350 downloaded standard versions.
To learn more about the substitution method, click here: https://brainly.com/question/26094713
#SPJ4
Question and choices are in the photo please explain the answer

Answers
Answer:
B
Step-by-step explanation:
expand the brackets
2x² - x + 10x -5 = 3x + 15
combine like terms
2x² + 9x - 5 = 3x + 15
2x² + 6x - 20 = 0
divide through by 2
x² + 3x - 10 = 0
factorise
determine factors of -10x² that would add up to 3x
they are 5x - 2x
(x² -2x) (5x - 10)
x(x - 2) +5(x-2)
x + 5 = 0
x = -5
x - 2 = 0
x = 2
Alice, Bob, and Carol were riding their bikes along the same path at different speeds. Alice's speed was twice Bob's speed, and Carols' speed was one-third that of Alice's speed. What was Carol's speed, in miles per hour, if Bob's speed was 9 miles per hour
Answers
Carol's speed is computed to be 6 miles/hour, solved using the equation (3x)/2 = 9.
We assume Carol's speed to be x miles/hours.
Carol's speed is given to be one-third of Alice's speed.
Then Alice's speed is three times Carol's speed, that is, Alice's speed = 3x miles/hour.
Alice's speed is given to be twice Bob's speed.
Then Bob's speed is half of Alice's speed, that is, Bob's speed = (3x)/2 miles/hour.
But, Bob's speed is given to be 9 miles per hour.
Therefore, we get the equation:
(3x)/2 = 9.
To find Carol's speed, we solve this equation as follows:
(3x)/2 = 9,
or, {(3x)/2}*2 = 9*2 {Multiplying both sides by 2},
or, 3x = 18 {Simplifying},
or, 3x/3 = 18/3 {Dividing both sides by 3},
or, x = 6 {Simplifying}.
Therefore, Carol's speed is computed to be 6 miles/hour, solved using the equation (3x)/2 = 9.
Learn more about solving equations at
https://brainly.com/question/27952911
#SPJ4
Solve each system.
[x-3 y =-1 -6 x+19 y =6 ]
Answers
The system of equations [x - 3y = -1 and -6x + 19y = 6] can be solved, resulting in x = -1 and y = 0.
To solve the system of equations [x - 3y = -1 and -6x + 19y = 6], we can use the method of substitution or elimination.
Let's solve it using the method of elimination.
First, we can multiply the first equation by 6 and the second equation by -1 to eliminate the x terms.
This gives us [6x - 18y = -6 and 6x - 19y = -6].
Now, subtracting the first equation from the second eliminates the x terms, leaving us with -y = 0. Solving for y, we find y = 0.
Substituting this value back into the first equation, we get x - 3(0) = -1, which simplifies to x = -1.
Therefore, the solution to the system of equations is x = -1 and y = 0.
Learn more about Equation click here :brainly.com/question/13763238
#SPJ1
select all options that represents the side lengths of a 30 60 90 triangle.

Answers
Answer:
Options (B) and (D)
Step-by-step explanation:
If a triangle is a 30° - 60° - 90° triangle, measure of the angle between the leg and hypotenuse will be either 60° or 90°.
Therefore, by applying Cosine rule in the given options.
c² = a² + b² - 2abCosC
All the given options are the right triangles.
[Since they follow the Pythagoras theorem]
Option (A),
Angle between the sides having measures 3 and 5 units,
4² = 3² + 5² - 2(3)(5)CosC
16 = 9 + 25 - 30.CosC
30.CosC = 18
\(C=\text{Cos}^{-1}(\frac{5}{6} )\)
C = 33.56°
Therefore, this triangle is not a 30-60-90 triangle.
Option (B),
Angle between the sides measuring 5 and 10 units,
\((5\sqrt{3})^2=5^2+10^2-2(5)(10)\text{CosC}\)
75 = 125 - 100(CosC)
Cos(C) = 0.5
C = 60°
Therefore, other angles of the triangle will be 30° and 90°.
And it's a 30°-60°-90° triangle.
Option (C),
10, 10, 10√2
It's a right triangle and the measure of legs are equal.
Since legs of this sides are equal, angles opposite to these equal sides will be equal.
Sum of all interior angles = 180°
m∠A + m∠B + m∠C = 180°
If m∠B = 90°
m∠A + 90° + m∠C = 180°
2(m∠A) = 90°
m∠A = 45°
Therefore, the given sides make a 45°- 45°- 90° triangle.
Option (D).
Angle between the sides 3 and 6,
(3√3)² = 3² + 6² -2(3)(6)CosC
27 = 9 + 36 - 36.(CosC)
CosC = \(\frac{18}{36}\)
C = \(\text{Cos}^{-1}(\frac{1}{2})\)
C = 60°
Therefore,
These sides make a 30°- 60°- 90° triangle.
Options (B) and (D) are the 30°- 60°- 90° triangle.
ten more than the quotient of c and three
Answers
The algebraic expression is,
⇒ 10 + c/3 = 12
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
The expression is,
''ten more than the quotient of c and three is 12.''
Now, We can formulate;
⇒ ten more than the quotient of c and three is 12
⇒ 10 + c/3 = 12
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ2
Complete question is this,
Ten more than the quotient of c and three is 12.
What is an equation of the line that passes through the point (4,2)(4,2) and is perpendicular to the line 4x+3y=214x+3y=21?
Answers
keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of the equation above
\(4x+3y=21\implies 3y=-4x+21\implies y=\cfrac{-4x+21}{3} \\\\\\ y=\stackrel{\stackrel{m}{\downarrow }}{-\cfrac{4}{3}}x+7\qquad \impliedby \qquad \begin{array}{|c|ll} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array} \\\\[-0.35em] ~\dotfill\)
\(\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{\cfrac{-4}{3}} ~\hfill \stackrel{reciprocal}{\cfrac{3}{-4}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{3}{-4}\implies \cfrac{3}{4}}}\)
so we're really looking for the equation of a line whose slope is 3/4 and it passes through (4 , 2)
\((\stackrel{x_1}{4}~,~\stackrel{y_1}{2})\hspace{10em} \stackrel{slope}{m} ~=~ \cfrac{3}{4} \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{2}=\stackrel{m}{ \cfrac{3}{4}}(x-\stackrel{x_1}{4}) \\\\\\ y-2=\cfrac{3}{4}x-3\implies {\Large \begin{array}{llll} y=\cfrac{3}{4}x-1 \end{array}}\)
What is the nature of roots of quadratic equation x^2 =- 2x 1?
Answers
The nature of roots of quadratic equation x² = -2x + 1 is real and distinct.
The standard form of a quadratic equation is:
ax² + bx + c = 0
The discriminant is defined as:
D = b² - 4ac
Using the value of discriminant, we can determine the nature of roots of a quadratic equation.
If:
D > 0, the quadratic equation has two distinct real roots or the roots are real and distinct.
D = 0, the quadratic equation has 1 real equal roots or the roots are unique
D < 0, the quadratic equation has complex conjugate roots or the roots are imaginary.
In this case, the quadratic equation is:
x² = -2x + 1
transform it into the standard form:
x² + 2x - 1 = 0
Calculate the discriminant:
D = 2² - 4 (-1) = 8
Since D > 0, the roots are two distinct real roots.
Your question is incomplete, but most probably your question was:
What is the nature of roots of quadratic equation x² = -2x + 1?
Learn more about quadratic equation here:
https://brainly.com/question/30097882
#SPJ4
A bookstore sells books at 25% profit calculate the percentage of sales price to cost price ?
Answers
Answer:
Cost price=100%
Step-by-step explanation:
What function is a vertical shift of f(x) = x?
A) g(x) = 3f(x)
B) g(x) = f(x - 3)
C) g(x) = f(x) + 4
D) g(x) = 1/2 f(x)
Answers
Answer:
C) g(x) = f(x) + 4
Step-by-step explanation:
A vertical shift is where you shift, slide or translate the whole graph up or down (on a graph) The way this shows up in the equation is just a number tacked on to the end of the equation. A +anumber (like the +4 in the answer) slides the function UP four units. A
-anumber would slide the function DOWN instead.
As for the other answers:
A) the 3multiplied in front is a vertical STRETCH.
D) the 1/2 multiplied in front is a vertical shrink (smash)
B) The -3 in close tight with the x is a horizontal shift(slide, translate) It is a RIGHT shift. A +anumber would be a LEFT shift. Horizontal shift seem kind of backwards. + goes LEFT and - goes RIGHT.
Solve the absolute value equation for x. |4 − 2x| + 6 = 18 Enter your answers in the blanks in order from least to greatest. x=□ or □
Answers
The solutions to the equation |4 − 2x| + 6 = 18, in order from least to greatest, are:
x = -4 or x = 8
What is inequality?
A solution for an inequality in x is a number such that when we substitute that number for x we have a true statement. So, 4 is a solution for example 1, while 8 is not. The solution set of an inequality is the set of all solutions.
We can solve this absolute value equation by first isolating the absolute value term on one side of the equation and then solving for both possible cases. Here are the steps:
|4 − 2x| + 6 = 18
|4 − 2x| = 12 (subtract 6 from both sides)
Now we have an absolute value equation with no constant term. We can split this equation into two cases: one where the expression inside the absolute value is positive, and one where it is negative. For each case, we can solve for x:
Case 1: 4 - 2x > 0
If 4 - 2x is positive, then we can drop the absolute value bars and write:
4 - 2x = 12
-2x = 8
x = -4
So one solution is x = -4.
Case 2: 4 - 2x < 0
If 4 - 2x is negative, then we must flip the inequality when dropping the absolute value bars:
-(4 - 2x) = 12
-4 + 2x = 12
2x = 16
x = 8
So the other solution is x = 8.
Therefore, the solutions to the equation |4 − 2x| + 6 = 18, in order from least to greatest, are:
x = -4 or x = 8
To learn more about inequality visit,
https://brainly.com/question/25944814
#SPJ1