A company estimates that 0. 5% of their products will fail after the original warranty period but within 2 years of the purchase, with a replacement cost of $500. 0. If they offer a 2 year extended warranty for $33. 00, what is the company's expected value of each warranty sold? Please format your answer using a dollar sign and two decimal points for the cents. For example, if the expected value was 50, please enter it as $50. 0
Answers
The expected value of each warranty sold is $2.47.
The expected value of each warranty sold can be calculated by subtracting the cost of the warranty from the expected value of the potential savings on replacement costs.
Let's assume that the company sells 1000 warranties. Then, the expected number of products that will fail within 2 years is:
0.5% of 1000 = 0.005 x 1000 = 5
The expected cost of replacing these products is:
5 x $500 = $2500
Therefore, the expected value of the warranty is:
($2500 - $33 x 1000) / 1000 = $2.47
To know more about expected value, refer to the link below:
https://brainly.com/question/13479504#
#SPJ11
Related Questions
10. A bag of flour for making pizza weighs 15 kilograms. An
award winning pizza maker uses 1.065 kilograms of flour every day
to make her killer pizzas. How much flour is left in her bag after 8
days?
Answers
Answer:
6.48
Step-by-step explanation:
she uses 1.065 every day for 8 days. 1.065 × 8 is 8.52. so that's how much she used in 8 days. theres 15 kilograms in the bag. 15(the original bag) - 8.52(how much was used) leaves you with the answer 6.48
John's son will start college in 10 years. John estimated a today's value of funds to finance college education of his son as $196,000. Assume that after-tax rate of return that John is able to earn from his investment is 8.65 percent compounded annually. He does not have this required amount now. Instead, he is going to invest equal amounts each year at the beginning of the year until his son starts college. Compute the annual beginning of-the-year payment that is necessary to fund the estimation of college costs. (Please use annual compounding, not simplifying average calculations).
Answers
John needs to make an annual beginning-of-the-year payment of approximately $369,238.68 to fund the estimated college costs of $196,000 in 10 years, given the after-tax rate of return of 8.65% compounded annually.
To compute the annual beginning-of-the-year payment necessary to fund the estimated college costs, we can use the present value of an annuity formula.
The present value of an annuity formula is given by:
P = A * [(1 - (1 + r)^(-n)) / r],
where P is the present value, A is the annual payment, r is the interest rate per period, and n is the number of periods.
In this case, John wants to accumulate $196,000 in 10 years, and the interest rate he can earn is 8.65% compounded annually. Therefore, we can substitute the given values into the formula and solve for A:
196,000 = A * [(1 - (1 + 0.0865)^(-10)) / 0.0865].
Simplifying the expression inside the brackets:
196,000 = A * (1 - 0.469091).
196,000 = A * 0.530909.
Dividing both sides by 0.530909:
A = 196,000 / 0.530909.
A ≈ 369,238.68.
Learn more about after-tax rate of return here:-
https://brainly.com/question/31825431?referrer=searchResults
#SPJ11
In a right triangle has one leg that measures 11 in and the hypotenuse measures 47 in, what is the length of the other leg?
Answers
Using the Pythagorean theorem:
47 ^2 = 11^2 + x^2
2209 = 121 + x^2
Subtract 131 from both sides
2088 = x^2
Take the square root of both sides
X = sqrt(2088)
Simplify
X = 6sqrt(58)
Almost every year, there is some incidence of volcanic activity on the island of Japan. In 2005 there were 5 volcanine episodes, defined as either eruptions or sizable seismic activity. Suppose the expected number of episodes is 2.4 per year. Let X be the number of episodes in the 2-year period 2008-2009.
(a) What model might you use to model X? Why? Justify the appropriateness of this model for this problem. Provide the parameter values for the model chosen.
(b) Using the model calculate the probability that there will be no episodes in this period?
(c) Using the model, calculate the probability that there are more than three episodes in this period.
Answers
a. The appropriate model for this problem is the Poisson distribution because it's model the number of rare events occurring in a fixed interval of time or space.
b. Using the model the probability that there will be no episodes in this period is 0.82%.
c. Using the model, the probability that there are more than three episodes in this period is 70.57%.
(a) The appropriate model for this problem is the Poisson distribution, which models the number of rare events occurring in a fixed interval of time or space. The conditions for a Poisson distribution are:
The events are rare or random.The events are independent of each other.The average rate of events is constant over time or space.In this case, we are interested in the number of volcanic episodes occurring in a 2-year period, which is a fixed interval of time. The events are rare and independent of each other, and the average rate of events is given as 2.4 per year. Therefore, the Poisson distribution is appropriate for modeling X.
The parameter value for the Poisson distribution is λ, the average rate of events per unit of time or space. In this case, λ = 2.4 x 2 = 4.8 for the 2-year period.
(b) The probability that there will be no episodes in this period is given by the Poisson probability mass function:
P(X = 0) = e^(-λ) * λ^0 / 0! = e^(-4.8) * 4.8^0 / 0! = 0.0082 (rounded to four decimal places)
Therefore, the probability that there will be no episodes in the 2008-2009 period is approximately 0.0082, or 0.82%.
(c) The probability that there are more than three episodes in this period is given by the complement of the probability that there are three or fewer episodes:
P(X > 3) = 1 - P(X ≤ 3)
We can use the Poisson cumulative distribution function to calculate P(X ≤ 3):
P(X ≤ 3) = Σ(e^(-λ) * λ^k / k!) for k = 0 to 3
P(X ≤ 3) = e^(-4.8) * (4.8^0 / 0! + 4.8^1 / 1! + 4.8^2 / 2! + 4.8^3 / 3!)
P(X ≤ 3) = 0.2943 (rounded to four decimal places)
Therefore, P(X > 3) = 1 - P(X ≤ 3) = 1 - 0.2943 = 0.7057 (rounded to four decimal places)
Therefore, the probability that there are more than three episodes in the 2008-2009 period is approximately 0.7057, or 70.57%.
To know more about Poisson distribution, refer:
brainly.com/question/28044733
#SPJ11
Least common multiple of 15,24 by using prime factorization
Answers
Answer and Step-by-step explanation:
The least common multiple (LCM) of 15 and 24 can be found using the prime factorization of 15 and 24 which is...
The prime factorization of 15 is... 3 x 5.
The prime factorization of 24 is... 2 x 2 x 2 x 3.
Eliminate the duplicate factors of the two, then multiply them once with the remaining factors of the lists to get LCM (15,15) = 120.
Hope this helped you out! Have a wonderful day! <3
Work out the area of this circle.
Take it to be 3. 142 and give your answer to 2 decimal places.
R: 9 m
Answers
The area of the circle is 63.62 square meters
To work out the area of a circle, we need to use the formula A = πr^2, where A is the area of the circle, π is a mathematical constant approximately equal to 3.142, and r is the radius of the circle.
In this problem, we are given the diameter of the circle, which is the distance across the circle passing through its center. The radius is half of the diameter, so we can find it by dividing the diameter by 2.
In this case, the diameter is 9 meters, so the radius is 9/2 = 4.5 meters. We then substitute this value into the formula:
A = πr^2
A = 3.142 x (4.5)^2
A = 3.142 x 20.25
A = 63.6175
A ≈ 63.62 square meters
Learn more about area here
brainly.com/question/28642423
#SPJ4
The given question is incomplete, the complete question is:
Work out the area of the circle where diameter is 9 meter
Take π it to be 3.142 and give your answer to 2 decimal places.
enter an algebraic expression for the word expression.
The quotient of -4 and y
Answers
Hey there!
Guide to follow
“Difference” means subtract
“Is” means equal to
“Product” means multiply
“Quotient” means divide
“Sum” means add
Answering your question….
“The [QUOTIENT] of [-4] and [y]
Remember we said “quotient” means divide
So we’re dividing -4 from y and that will be your answer.
Answer
-4 ÷ y
Good luck on your assignment and enjoy your day!
~Amphitrite1040:)
I’ll give brainliest
Completed a full explanation of statistics with explanation and examples ?
Answers
Answer: Hope This Helps!
Step-by-step explanation:
Statistic Definition: A mathematical science concerned with data collection, presentation, analysis, and interpretation
Examples: "Statistics is the only mathematical field required for many social sciences." and "The statistics from the Census for apportionment are available."
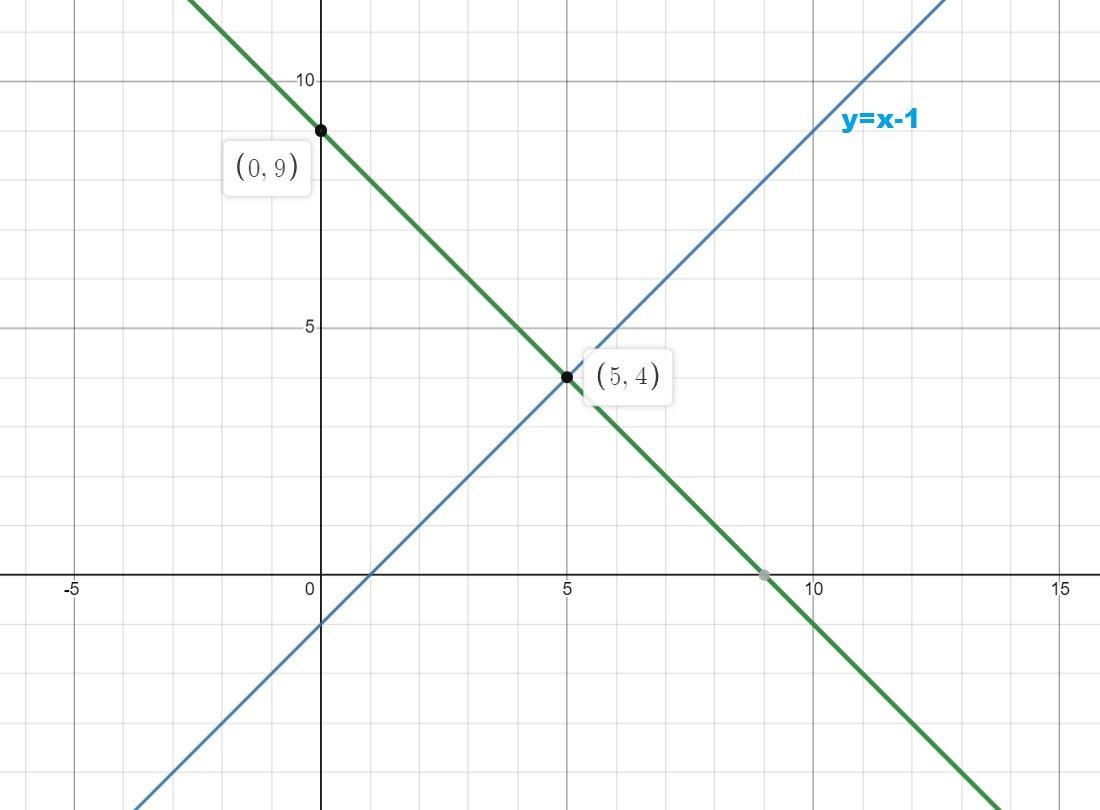
quick Sarah is walking diagonally across a park as modeled by the equation y = x − 1. Suppose Marcus starts walking at the point (0, 9) so his path is perpendicular to Sarah's. At what point will Sarah's path and Marcus's path intersect?
Answers
The Sarah's path and Marcus path will intersect at the point (5,4) .
In the question ,
it is given that
the park is modeled by the equation y = x − 1 .
On comparing with the slope intercept form ,
we get
the slope as 1 .
Since both the paths are perpendicular ,
the slope for Marcus path is -1 .
hence the equation of line with slope -1 and passing through the point (0,9) is y = (-1)x + c
9 = (-1)0 + c
9 = c
so equation is y = (-1)x + 9
So to find the point of intersection , we solve both the equations .
Substituting y = x − 1 in y = (-1)x + 9 ,
we get
x − 1 = (-1)x + 9
x - 1 = -x + 9
x + x = 9 + 1
2x = 10
x = 5
So, y = 5 - 1 = 4
the point of intersection is (5,4) .
Therefore , The Sarah's path and Marcus path will intersect at the point (5,4) .
Learn more about Equations here
https://brainly.com/question/19700463
#SPJ1
A square notepad has sides that are 10 centimeters long. What is the notepad's area?
Answers
Answer:
100cm²
Step-by-step explanation:
The notepad is square.
The area of a square = length X width.
All the sides of a square are the same length.
Therefore, the area of the notepad = 10 X 10 which equals 100.
Don't forget the units!
The units for area is cm².
The units for volume is cm³.
This is area so your answer is 100cm².
Hope this helped, have a nice day!
Convert the Senary (base 6 number 54724 to decimal
Answers
Answer: To convert a Senary (base 6) number to decimal, we can use the following formula:
Decimal = (5 * 6^4) + (4 * 6^3) + (7 * 6^2) + (2 * 6^1) + (5 * 6^0)
= (5 * 1296) + (4 * 216) + (7 * 36) + (2 * 6) + (5 * 1)
= 6480 + 864 + 252 + 12 + 5
= 7603
So the Senary (base 6) number 54724 is equivalent to the decimal number 7603.
Step-by-step explanation:
the average person requires 2000 calories per day to sustain normal activity. how many 60 w light bulbs is this equivalent to? over the course of a year, how many gallons of gasoline is this equivalent to?
Answers
0.017 gallons, or around 1/60 of a gallon, is the amount of gasoline that would be equivalent.
In the given question, we have to find the equivalent number of light bulbs.
We can use the equation:
Number of light bulbs = (Calories / Bulb efficiency) / Bulb wattage
Where Calories is the number of calories required, Bulb efficiency is the number of calories per watt-hour of the light bulb, and Bulb wattage is the power rating of the light bulb in watts.
The amount of energy a light bulb converts to visible light determines its efficiency. For a 60 W incandescent light bulb, the efficiency is typically around 15 lumen's per watt.
Since 4.1868 joules make up one calorie, the bulb's efficiency in terms of calories per watt-hour is:
Bulb efficiency = (15 lumen's/watt) * (4.1868 joules/calorie) / (1 watt-hour)
Bulb efficiency = 62.8 calories/watt-hour
Plugging in the values, we get:
Number of light bulbs = (2000 calories / 62.8 calories/watt-hour) / 60 W
Number of light bulbs = 0.32 light bulbs
So the equivalent number of light bulbs is about 0.32 light bulbs, or about 1/3 of a light bulb.
To find the equivalent number of gallons of gasoline, we can use the equation:
Number of gallons of gasoline = (Calories / Gasoline energy density) / (Gasoline efficiency * Miles per gallon)
Where Calories is the number of calories required, Gasoline energy density is the energy content of gasoline in calories per gallon, Gasoline efficiency is the number of miles per gallon a car can travel, and Miles per gallon is the number of miles a car can travel on a gallon of gasoline.
The energy density of gasoline is around 116,090 calories per gallon. The efficiency of a car is typically around 25 miles per gallon.
Plugging in the values, we get:
Number of gallons of gasoline = (2000 calories / 116,090 calories/gallon) / (25 miles/gallon)
Number of gallons of gasoline = 0.017 gallons
Therefore, 0.017 gallons, or around 1/60 of a gallon, is the amount of gasoline that would be equivalent.
To learn more about Bulb efficiency link is here
brainly.com/question/14450944
#SPJ4
The right question is:
The average person requires 2000 calories per day to sustain normal activity. How many 60 W light bulbs is this equivalent to? Over the course of a year, how many gallons of gasoline is this equivalent to?
(1) 2 light bulbs, 30 gallons of gasoline
(2) 5 light bulbs, 50 gallons of gasoline
(3) 1 light bulb, 20 gallons of gasoline
(4) 4 light bulbs, 100 gallons of gasoline
What number should be placed in the box to help complete the division calculation?

Answers
70/13=5.3
We take just 5
The weights of apples sold in a Toronto supermarket are independently distributed with mean I and variance 02. Spencer draws a random sample of n apples from this supermarket, with their weights denoted as X1, X2,... Xn. Spencer uses the average weights of the first apple and the last apple as an estimator of ji. What is the sampling variance of Spencer's estimator?
Answers
The sampling variance of Spencer's estimator can be calculated using the formula for the variance of the sum or difference of two random variables.
In this case, Spencer's estimator is the average weight of the first and last apple, denoted as (X1 + Xn)/2.
The variance of the sum or difference of two independent random variables is the sum of their individual variances. Since the weights of the apples are independently distributed with mean µ and variance σ^2, the variance of each apple weight is σ^2.
To find the sampling variance of Spencer's estimator, we need to find the variance of (X1 + Xn)/2. Using the formula for variance, we can simplify the calculation as follows:
Var[(X1 + Xn)/2] = (1/4) * Var(X1 + Xn)
Since X1 and Xn are independent, the variance of their sum is the sum of their individual variances:
Var(X1 + Xn) = Var(X1) + Var(Xn) = 2σ^2
Plugging this back into the previous equation, we get:
Var[(X1 + Xn)/2] = (1/4) * 2σ^2 = σ^2/2
Therefore, the sampling variance of Spencer's estimator is σ^2/2.
To know more about calculated , visit ;
https://brainly.com/question/30151794
#SPJ11
What are the 6 basic graphs?
Answers
The six different types of graphs are frequency distribution graphs, exponential graphs, logarithmic graphs, trigonometric graphs, and statistical graphs (such as bar, pie, and line graphs).
A vertical and horizontal line connect at the origin to form a simple two-dimensional graph. The x axis is horizontal, whereas the y axis is vertical. The x and y axes in basic line graphs are each subdivided into uniformly spaced subdivisions and given integer values.
There are eight primary types of graphs: linear, power, quadratic, polynomial, and they all aid in organising the presentation of data or information.
To know more about graphs, visit,
https://brainly.com/question/19040584
#SPJ4
please help thank you!!!

Answers
Answer:
s = 11.7 ft
Step-by-step explanation:
The bedroom is square, and the area A is equal to 137 ft^2.
Since the area formula for a square is A = s^2, s = √A.
Here, s = √137 ft, or s = 11.7 ft (to the nearest tenth of a ft)
$17.99 with an 11.25% tax
Answers
Answer:
it's 2.0
hope that helps

find the mean, lower quartile, and highest quartile of 53, 49, 52, 71, 67, 51, 63, 49, 58
Answers
Answer:
the mean is 61.44, the lower quartile is 51, and the upper quartile is 65
Step-by-step explanation:
we need to first sort the data in ascending order:
49, 49, 51, 52, 53, 58, 63, 67, 71
The mean is the average of all the numbers in the data set:
Mean = (49 + 49 + 51 + 52 + 53 + 58 + 63 + 67 + 71) / 9 = 553 / 9 = 61.44 (rounded to two decimal places)
To find the lower quartile, we need to find the median of the lower half of the data set. Since there are an odd number of values in the data set, we exclude the median value from the lower half. The lower half of the data set is:
49, 49, 51, 52, 53
The median of the lower half is the middle value, which is 51. Therefore, the lower quartile is 51.
To find the upper quartile, we need to find the median of the upper half of the data set. Again, we exclude the median value from the upper half since there are an odd number of values. The upper half of the data set is:
58, 63, 67, 71
The median of the upper half is the middle value, which is (63 + 67) / 2 = 65. Therefore, the upper quartile is 65.
Answer: Lower quartile=51.5, mean=58, and highest quartile=65.
Step-by-step explanation: To find the lower quartile you have to find the median of the lower half. In this case, the lower half is 49, 51, 52, and 53. Since there are two numbers, we have to find the average of them (51, 52). To find the average, add them together, which would be 103. Now, divide 103 by 2 which would be 51.5 (the lower quartile). To find the mean, add all the numbers together (464) and divide them by the number of numbers that are on there (8). So, 464/8 is 58. To find the highest quartile, find the median of the upper half. In this case, we have find the average of 63 and 67. So, add 63 and 67 which would be 130, and divide by 2 (which would be 65). Hope this helped and have a great day!
how to calculate perimeter
Answers
Answer:
To calculate perimeter add all the sides of the particular shape.
I hope this helps!
Square perimeter formula: P = 4a
Rectangle perimeter formula: P = 2(a + b)
Triangle perimeter formulas:
P = a + b + c or
P = a + b + √(a² + b² - 2ab * cos(γ)) or
P = a + (a / sin(β + γ)) * (sin(β) + sin(γ))
Circle perimeter formula: P = 2πr
Circle sector perimeter formula: P = r(α + 2) (α is in radians)
Ellipse perimeter formula: P = π(3(a + b) - √((3a + b) * (a + 3b)))
Quadrilateral / Trapezoid perimeter formula: P = a + b + c + d
Parallelogram perimeter formulas:
P = 2(a + b) or
P = 2a² + √(2e² + 2f² - 4a²) or
P = 2(b + h/sin(α))
Rhombus perimeter formulas:
P = 4a or
P = 2√(e² + f²)
Kite perimeter formula: P = 2(a + b)
Annulus perimeter formula: P = 2π(R + r)
Regular polygon area formula: P = n * a
Leah Deposited $7000 in an account that earns 2% interest compounded annually. How much interest will she have earned after 6 years?
Answers
Answer:
840
Step-by-step explanation:
7000×2×6 ÷ 100. since it is 2%
= 840
HELP ME PLEASE
20 POINTSSS
5. Use the distributive property to write each of the following expressions as the sum of monomials.
1/3(12z+18z^2)
Answers
Answer:
4z + 6z²
Step-by-step explanation:
\(\frac{1}{3}\) (12z + 18z² ) ← multiply each term in the parenthesis by \(\frac{1}{3}\)
= 4z + 6z²
Selected values of a continuous functionſ are given in the table above. Which of the following statements could be false? By the Intermediate Value Theorem applied to f on the interval (2,5), there is a value c such that f(c) = 10. By the Mean Value Theorem applied to f on the interval (2,5), there is a value c such that f'(c) = 10. (c) By the Extreme Value Theorem applied to f on the interval 2,5), there is a value c such that f(e)s () for all in (2,5). By the Extreme Value Theorem applied to f on the interval 2,5), there is a value c such that s ) 2 (2) for all in 2,5
Answers
The table has
x values 2,3,4,5 and
f(x) as 1, 14,20, 31
The statements A is true Intermediate value theorem, B is false mean value theorem, C is true extreme value theorem and D is true.
Given that,
The table has
x values 2,3,4,5 and
f(x) as 1, 14,20, 31
The function f is continuous.
A is true, From the figure.
Intermediate value theorem is let [a,b]be a closed and bounded intervals and a function f:[a,b]→R be continuous on [a,b]. If f(a)≠f(b) then f attains every value between f(a) and f(b) at least once in the open interval (a,b).
B is false because, mean value theorem, Let a function f:[a,b]→R be such that,
1. f is continuous on[a,b] and
2. f is differentiable at every point on (a,b).
Then there exist at least a point c in (a,b) such that f'(c)=(f(b)-f(a))/b-a
In the B part, the differentiability is not given do mean value theorem can be applied.
C is true because the extreme value theorem, if a real-valued function f is continuous on the closed interval [a,b] then f attains a maximum and a minimum each at least once such that ∈ number c and d in[a,b] such that f(d)≤f(x)≤f(c)∀ a∈[a,b].
D is true.
Therefore, The statements A is true, B is false, C is true and D is true.
To learn more about theorem visit: https://brainly.com/question/4940880
#SPJ4

simplify the following without a calculator leave your answer with positive exponents
\((0.008) \frac{2}{3} \)
Answers
How do you find theGreatest common factor for 15 and 40
Answers
Answer:
See Explanation
Step-by-step explanation:
\(15 = 3 \times \bold{ \red{ \boxed5}} \\ \\ 40 = 2 \times 2 \times 2 \times \bold{ \purple{ \boxed5}} \\ \\ common \: factor \: of \: 15 \: and \: 40= 5 \\ \\ \therefore \: gcf \: of \: 15 \: and \: 40 = 5\)
12. Write the MATLAB statements required to calculate f(t) using the following equation for values of t € [-9,9] in steps of 0.5. f(t) = { (-3t² +5 t 20 3t² +5 t < 0 13. Write a MATLAB function named UniGen that generates a specified number (n) of random values that are uniformly distributed on any given interval specified by values a and b, that is, [a, b].
Answers
12. MATLAB code: `f = (-3*t.^2 + 5*t + 20).*(t < 0) + (3*t.^2 + 5*t).*(t >= 0)`
13. MATLAB function: `function random_values = UniGen(n, a, b); random_values = (b - a) * rand(n, 1) + a; end`
MATLAB code to calculate f(t) using the given equation:
t = -9:0.5:9; % Generate values of t from -9 to 9 in steps of 0.5
f = zeros(size(t)); % Initialize f(t) vector
for i = 1:numel(t)
if t(i) < 0
f(i) = -3*t(i)^2 + 5*t(i) + 20;
else
f(i) = 3*t(i)^2 + 5*t(i);
end
end
% Display the results
disp('t f(t)');
disp('--------');
disp([t' f']);
```
This code generates values of `t` from -9 to 9 in steps of 0.5 and calculates `f(t)` based on the given equation. The results are displayed in a tabular format showing the corresponding values of `t` and `f(t)`.
13. MATLAB function UniGen to generate uniformly distributed random values:
function random_values = UniGen(n, a, b)
% n: Number of random values to generate
% a: Start of the interval
% b: End of the interval
random_values = (b - a) * rand(n, 1) + a;
end
This MATLAB function named `UniGen` generates `n` random values that are uniformly distributed on the interval `[a, b]`. It utilizes the `rand` function to generate random values between 0 and 1, which are then scaled and shifted to fit within the specified interval `[a, b]`. The generated random values are returned as a column vector.
Learn more about MATLAB code
brainly.com/question/12950689
#SPJ11
find the point on the surface 6x=y2+z2 so that its tangent plane is parallel to
Answers
To find the point on the surface 6x = y^2 + z^2 where its tangent plane is parallel to a given plane, we need to find a point on the surface and determine the normal vector of the surface at that point.
Then, we can compare the normal vector of the surface to the normal vector of the given plane to check if they are parallel.
Let's first find a point on the surface by substituting a value for either y or z and solving for x. Let's choose y = 0:
6x = 0^2 + z^2
6x = z^2
x = z^2/6
So, one point on the surface is (z^2/6, 0, z).
To find the normal vector of the surface at this point, we can calculate the partial derivatives with respect to x, y, and z:
∂/∂x (6x) = 6
∂/∂y (y^2 + z^2) = 0
∂/∂z (y^2 + z^2) = 2z
The normal vector is then N = (6, 0, 2z) = (6, 0, 2z) / ||(6, 0, 2z)||, where ||N|| represents the magnitude of N.
To determine if the tangent plane is parallel to a given plane, we compare the normal vector of the surface to the normal vector of the given plane. If they are parallel, their direction vectors should be proportional.
If the given plane is parallel to the xy-plane and has a normal vector N_1 = (0, 0, 1), we can compare it to the normal vector of the surface. In this case, we see that the z-component of N (2z) is not proportional to the z-component of N_1 (1). Therefore, the tangent plane of the surface at the chosen point is not parallel to the given plane.
To find a point on the surface where its tangent plane is parallel to the given plane, we would need to choose a different point on the surface such that the normal vector of the surface at that point is parallel to the given plane's normal vector.
Learn more about Tangent here -: brainly.com/question/26153770
#SPJ11
Two way table Probability (100 points awarded)
If a student is selected at random find the probability the student is a freshman. P(Freshman) =
Round to the nearest whole percent.

Answers
Answer:
Out of the 4 + 6 + 2 + 2 + 3 + 4 + 6 + 3 = 30 total students, 4 + 3 = 7 are freshmen so the answer is 7 / 30 * 100 = 23%.
Step-by-step explanation:
Joe is spinning a spinner that is broken into 4 equal parts and labeled 1-4. Which answer choice below represents approximately how many times you would expect the spinner to land on a 3 if spun 50 times?
Answers
Approximately 12.5 times, or rounded to the nearest whole number, we would expect the spinner to land on a 3 if spun 50 times.
To determine the expected number of times the spinner would land on a 3 if spun 50 times, we need to consider that the spinner has 4 equal parts labeled 1-4.
Since the spinner is broken into 4 equal parts, we can assume that each outcome (landing on a specific number) has an equal probability of occurring. Therefore, the probability of landing on a 3 is 1 out of 4 or 1/4.
To find the expected number of times, we multiply the probability of landing on a 3 (1/4) by the total number of spins (50):
Expected number of times = Probability of landing on a 3 * Total number of spins
= (1/4) * 50
= 12.5
Therefore, approximately 12.5 times, or rounded to the nearest whole number, we would expect the spinner to land on a 3 if spun 50 times.
Visit here to learn more about whole number brainly.com/question/29766862
#SPJ11
How is 4.209 written using words?
Answers
Answer:
Four and two hundred nine thousandths
Answer
four and two hundred nine thousandths. or, simpler: four point two hundred nine. or, even simpler: four point two zero nine.
Step-by-step explanation:
What's the inverse of f x )= 1 4x 7?
Answers
The inverse of f is a function which takes any value x and divides it by 4, then adds 7 to the result.
The inverse of a function is the opposite of the original function, meaning that it takes the output of the original function and turns it back into the input. In this case, the original function is f(x)=1/4x+7. To find the inverse, we need to solve for x in the equation, which can be done by subtracting 7 from both sides and then multiplying both sides by 4. This gives us x=(x+7)/4, which is the inverse of the original function. To put it simply, the inverse of f takes any output of the original function, adds 7 to it, and then divides it by 4 to get the original input.
example;
If f(x)=1/4x+7 and x=3, then
f(3) = (1/4)3 + 7
7.75
The inverse of f is f^-1(x) = (x + 7) / 4.
If f^-1(7.75) = (7.75 + 7) / 4, then
f^-1(7.75) = 14.75 / 4
3.6875
Learn more about inverse here
https://brainly.com/question/13715269
#SPJ4