✓ A G.P has 6 terms. If the 3rd 4th term and are 28 and -56 respectively. Find (a) the common ratio (b) the first term (c) the sum of the G.P.​

The  probability of event A is P(A) = 1/4 or 0.25.

The formula to find P(A) for a series of simple events is:

P(A) = (number of outcomes that satisfy the event A) / (total number of possible outcomes)

For example, if you are tossing a coin and selecting a number at the same time, and event A is defined as getting a head and an even number, then:

- The number of outcomes that satisfy event A is 1 (getting a head and an even number, i.e., H2)
- The total number of possible outcomes is 4 (H1, H2, T1, T2)
- Therefore, the probability of event A is P(A) = 1/4 or 0.25.

Visit to know more about Probability:-

brainly.com/question/13604758

#SPJ11

In order to divide a couple of functions, we simply divide their equations:

if f(x) = 25 - x²

and g(x) = x + 5

then

In order to simplify the fraction we just factor the numerator:

25 - x² = (5 + x) (5 - x)

then

Since

5 + x = x + 5

we can cancel this factor from the denominator:

then,

Answer: (f/g)(x) = 5 - x

The equation of the tangent line to y at x = 6 is f'(6)(x - 6) + f(6), where f'(6) = g'(6) and f(6) = In[1 + g(0)].

To find the equation of the tangent line, we need the slope and a point on the line. The slope is given by f'(6), which is equal to g'(6). The point on the line can be determined by evaluating f(6), which is In[1 + g(0)]. By substituting these values into the point-slope form of a line equation, we obtain the equation of the tangent line.

To explain it in more detail, we start with the function f(x) = In[1 + g(0)]. The function g(x) is not explicitly given, but we are given specific information about g(6) and g'(6).

We are told that g(6) = 0 - 1, which means g(6) = -1. Additionally, we are given g'(6) = 8e, where e is the mathematical constant approximately equal to 2.71828.

Now, to find the equation of the tangent line to y at x = 6, we need to determine the slope of the tangent line and a point on the line.

The slope of the tangent line is given by f'(6). Since f(x) = In[1 + g(0)], we can differentiate this function with respect to x to find f'(x). However, since we are only interested in the value at x = 6, we can use the chain rule to find f'(6).

Using the chain rule, we have f'(x) = (1 / (1 + g(0))) * g'(x), where g'(x) represents the derivative of g(x) with respect to x.

Plugging in the known values, we have f'(6) = (1 / (1 + g(0))) * g'(6) = (1 / (1 + g(0))) * 8e.

Next, we need to find a point on the line. We can evaluate f(6) by substituting the value of g(0) into the function f(x). From the given information, we know that g(0) = -1. Thus, f(6) = In[1 + (-1)] = In[0] = -∞.

Now, we have the slope f'(6) = (1 / (1 + g(0))) * 8e and the point (6, -∞).

Finally, we can use the point-slope form of a line equation to find the equation of the tangent line. The point-slope form is y - y1 = m(x - x1), where (x1, y1) is the given point and m is the slope.

Substituting the values, we have y - (-∞) = f'(6)(x - 6), which simplifies to y = f'(6)(x - 6) + (-∞). Since (-∞) is not a precise value, we omit it from the equation, giving us the final answer: y = f'(6)(x - 6).

Learn more about equation here:

https://brainly.com/question/29538993

#SPJ11

Answer:

It's a scalene triangle

Step-by-step explanation:

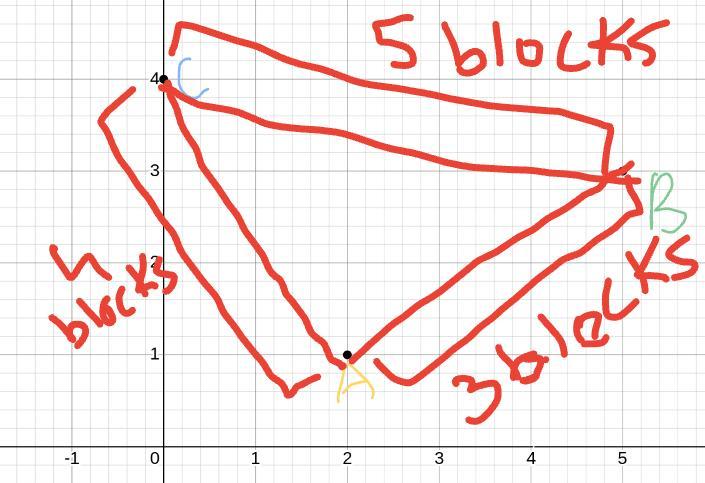
I graphed each point and here's the picture.

You can see how from point C to A is a distance of 4 blocks,

distance from point A to B is 3 blocks, and B to C is 5 blocks.

So this triangle is a scalene triangle.

Answer:

scalene

Step-by-step explanation:

from A to B

the difference is x's is 3

the difference in y's is 2

3^2 + 4^2 = 9 +16 = 25, square of 25 is 5

from B to C

x's : 5 and y's : 4

25+ 16 = 36

the square root of 36 is 6

fromA to C

x's :4 and y's : 3

16 + 9 = 25 . the square root of 25 is 5

the dimensions of the triangle are 4,5,6

all the sides are different so is scalene

Answer:

1)I don't know

2)-2

Step-by-step explanation:

2)6-5(1/1/x)= 2

6-5(1/1)-x= 2

6-6-x=2

-x/-1=2/-1

x= -2

Answer:

Step-by-step explanation:

8x+2y=16

2y=-8x+16

y=-4x+8

slope is -4

y-intercept is (0,8)

x-intercept is (2,0)

Answer:

slope = -4

y-intercept = (0,8)

x-intercept = (2,0)

Step-by-step explanation:

To find the slope:

8x + 2y = 16. First get the y by itself.

2y = -8x + 16. Then divide by 2

y = -4x + 8. So the slope is -4.

y-intercept:

8x+2y=16

8(0)+2y=16

2y=16

y=8

y-int: (0,8)

x-intercept:

8x+2y=16

8x+2(0)=16

8x=16

x=2

x-int: (2,0)

Answer:

5 is how many he did not hit

No, The range of r contains points that are not in the domain of f.

Calculus is a branch of mathematics that deals with the study of rates of change, accumulation, and mathematical modeling of continuous quantities.

The correct answer is: No. The range of r contains points that are not in the domain of f.

In order for a function to be integrable along a curve, the curve must lie entirely within the domain of the function. The domain of a function is the set of all possible input values for which the function is defined.

In this case, the function f(x, y, z) = x ln(yz) has a domain that depends on the values of x, y, and z. However, the curve C, parametrized by r(t) = et², ln(t) + 1/2, t³ - 2, where 0 ≤ t ≤ e, may contain points that fall outside the domain of f.

Hence, f may not be integrable along C because the range of r (i.e., the set of all possible points traced by C) contains points that are not in the domain of f.

To learn more about domain & range, Visit

https://brainly.com/question/28135761

#SPJ1

Answer: 8,437

Step-by-step explanation:

Hope this helps bro. Good day mate!

One of the solutions to the equation include the following: C) (1, 4)

In order to determine which ordered pairs are valid and true solutions based on the given linear equation, we would have to test the given ordered pairs by substituting their values into the given equation as follows;

For ordered pair (4, 4), we have:

x³ + 4x² − 2x + 1 = x + 3

(4)³ + 4(4)² − 2(4) + 1 = 4 + 3

121 ≠ 7

For ordered pair (6, 2), we have:

x³ + 4x² − 2x + 1 = x + 3

(6)³ + 4(6)² − 2(6) + 1 = 6 + 3

349 ≠ 9

For ordered pair (1, 4), we have:

x³ + 4x² − 2x + 1 = x + 3

(1)³ + 4(1)² − 2(1) + 1 = 1 + 3

4 = 4

Read more on ordered pairs here: brainly.com/question/12179097

#SPJ1

Answer: 1346.2 Milimeters

Step-by-step explanation:

4ft 5in = 53in

53x25.4= 1346.2

The loan term of the truck is average between 1-7 years, depending on the lender and the type of loan.

The loan term of the truck is typically determined by the lender and the type of loan. Most lenders offer terms ranging from 1 to 7 years, although some may offer longer terms. The loan term is the length of time it takes to pay off the loan in full. Generally, the longer the loan term, the lower the monthly payments and the higher the overall cost of the loan due to interest costs. Shorter loan terms typically have higher monthly payments but lower overall costs as there is less interest to pay over the life of the loan. The loan term can also affect the interest rate, with shorter terms typically offering lower rates than longer terms. It's important to consider all of these factors before deciding on a loan term.

Learn more about average here

https://brainly.com/question/24057012

#SPJ4

Answer:

x=3

Step-by-step explanation:

Step 1: Simplify both sides of the equation.

1/2−x+3/2=x−4

1/2+−x+3/2=x+−4

(−x)+(1/2+3/2)=x−4(Combine Like Terms)

−x+2=x−4

−x+2=x−4

Step 2: Subtract x from both sides.

−x+2−x=x−4−x

−2x+2=−4

Step 3: Subtract 2 from both sides.

−2x+2−2=−4−2

−2x=−6

Step 4: Divide both sides by -2.

−2x/−2=−6/−2

x=3

87(x) = 3,562

Solve for x

divide by 87 on both sides

Answer x = about 41

on average each costumer spent about 41 dollars,

Answer:

average spent per customer = total sales / number of customers

average spent per customer = $3,562 / 87 = $40.82

An estimator is said to be unbiased if the expected value of the estimator is equal to the true value of the parameter being estimated.

Unbiased estimators are useful because they provide an estimate that, on average, is equal to the true value of the parameter, making them desirable for making accurate inferences about a population.

In statistics, an estimator is a statistic used to estimate the value of an unknown parameter in a population. An estimator is said to be unbiased if, on average, it produces an estimate that is equal to the true value of the parameter. An unbiased estimator is desirable because it provides an estimate that is, on average, accurate, which is important for making inferences about a population.

Biased estimators, on the other hand, tend to consistently overestimate or underestimate the true value of the parameter, which can lead to incorrect conclusions. Therefore, unbiased estimators are useful because they provide more accurate estimates, which can lead to more reliable inferences about a population.

You can learn more about Unbiased estimators at

https://brainly.com/question/29646467

#SPJ11

The maximum profit is achieved when approximately 312.5 units of lab equipment are sold.

The revenue function R(x) represents the amount of money the company earns from selling x units of lab equipment. It is given by the equation:

R(x) = -0.32x^2 + 270x

The costs function C(x) represents the expenses incurred by the company for producing and selling x units of lab equipment. It is given by the equation:

C(x) = 70x + 52

To determine the company's profit, we subtract the costs from the revenue:

Profit = Revenue - Costs

P(x) = R(x) - C(x)

Substituting the given revenue and costs functions:

P(x) = (\(-0.32x^2 + 270x)\) - (70x + 52)

Simplifying the equation:

P(x) = -0.32x^2 + 270x - 70x - 52

P(x) = -\(0.32x^2\)+ 200x - 52

The profit function P(x) represents the amount of money the company makes from selling x units of lab equipment after deducting the costs. It is a quadratic function with a negative coefficient for the x^2 term, indicating a downward-opening parabola. The vertex of the parabola represents the maximum profit the company can achieve.

To find the maximum profit and the corresponding number of units sold, we can use the vertex formula:

x = -b / (2a)

For the profit function P(x) = -\(0.32x^2 + 200x\)- 52, a = -0.32 and b = 200.

x = -200 / (2 * -0.32)

x = 312.5

Therefore, the maximum profit is achieved when approximately 312.5 units of lab equipment are sold.

for more such question on profit visit

https://brainly.com/question/29785281

#SPJ8

Answer:

x = 15

Step-by-step explanation:

Step 1: Define

j(x) = -4/5x + 7

j(x) = -5

Step 2: Substitute and Evaluate

-5 = -4/5x + 7

-12 = -4/5x

x = 15

Answer: 90

Step-by-step explanation: I multiplied 18 by 5

Answer:

H=90

Step-by-step explanation:

if H÷5=18, then reverse it. so 18×5=90

If one is interested in measuring the effects of a moderating variable, one can build it into the design as an independent variable.

To measure the effects of a moderating variable, it can be built into the design as an independent variable.

When studying the relationship between two variables, a moderating variable is a factor that influences the strength or direction of the relationship.

It is also known as an interaction variable. In order to measure the effects of a moderating variable, it is important to incorporate it into the research design.

To build a moderating variable into the design, it is treated as an independent variable.

An independent variable is a variable that is manipulated or controlled by the researcher.

By including the moderating variable as an independent variable, researchers can examine how it interacts with the other variables of interest.

The moderating variable is often operationalized by creating different groups or conditions based on its levels. For example, in a study investigating the impact of teaching method (independent variable) on student performance (dependent variable), the moderating variable could be student motivation.

The researchers can build the moderating variable into the design by dividing participants into high and low motivation groups, and then examining how the teaching method affects their performance differently.

By incorporating the moderating variable as an independent variable, researchers can systematically examine its influence on the relationship between the other variables. This allows for a deeper understanding of how and under what conditions the relationship changes.

Learn more about moderating variable here:

https://brainly.com/question/31597586

#SPJ11

A decimal and fraction and shaded part of the first diagram second diagram is 100/100 or 1 and 0.63 or 63/100 respectively.

What is fraction?

A fraction is a way of expressing a part of a whole, or a part of a group, by using two numbers separated by a line. The number above the line is called the numerator, and the number below the line is called the denominator.

The first 10 by 10 matrix is fully colored, which means all 100 cells are colored. Therefore, the fraction of colored cells is:

100/100 = 1

The decimal representation of this fraction is simply 1.

For the second 10 by 10 matrix, the first 6 columns are fully colored, which means there are 6 x 10 = 60 colored cells. The 7th column has only the first 3 rows colored, which means there are 3 colored cells in this column. Therefore, the total number of colored cells is:

60 + 3 = 63

The fraction of colored cells is:

63/100

To convert this fraction to a decimal, we can divide the numerator by the denominator:

63 ÷ 100 = 0.63

Therefore, the shaded part of the second matrix is 0.63 or 63/100.

To learn more about fraction visit:

https://brainly.com/question/78672

#SPJ1

Answer:

1.54 and 1.7 I believe

Step-by-step explanation:

Answer:

The full steel tire is 1.76 pounds and the lighter wheel is 1.54 pounds

Step-by-step explanation:

To find how many pounds each tire is, divide the weight in grams by 453.592

Full steel tire:

800/453.592 = 1.76 pounds

Lighter wheel:

700/453.592 = 1.54 pounds

So, the full steel tire is 1.76 pounds and the lighter wheel is 1.54 pounds

(a) sin⁻¹(-1/2) = -π/6, (b) sin⁻¹(3√2) does not have a solution in the interval [-π/2,π/2]. (c) sin⁻¹(-3√2) does not have a solution in the interval [-π/2,π/2].

(a) The inverse sine function sin⁻¹(x) returns the angle whose sine is x. In this case, we want to find the angle whose sine is -1/2. Since the sine function is negative in the third quadrant and the range of sin⁻¹(x) is [-π/2,π/2], the angle we are looking for is in the fourth quadrant.

Therefore, we use the reference angle π/6 and add a negative sign to get -π/6 as our final answer.

(b)  The inverse sine function sin⁻¹(x) returns the angle whose sine is x. In this case, we want to find the angle whose sine is 3√2. However, since the range of the sine function is [-1,1], there is no angle whose sine is greater than 1.

Therefore, this expression does not have a solution in the interval [-π/2,π/2].

(c)  The inverse sine function sin⁻¹(x) returns the angle whose sine is x. In this case, we want to find the angle whose sine is -3√2. However, since the range of the sine function is [-1,1], there is no angle whose sine is less than -1.

Therefore, this expression does not have a solution in the interval [-π/2,π/2].

To know more about inverse sine function, refer here:
https://brainly.com/question/28468393#
#SPJ11

The equations that represent the information given in the problem are  r + a = 5 and 3r + 6a = 20 respectively. The correct options are (b) and (c).

A system of linear equations is a group of  equations having same number of variables and degree.

For the n number of variables n number of equations are required.

On the basis of number of solutions a system of equations can be classified as consistent and inconsistent.

The total weight of mixture is 5 pound.

And, the cost per pound is $4.

Then, the cost of a bag of 5 pound is 4 × 5 = $20.

Suppose the amount of raisin in 5 pound bag be r and that of almond be a.

Now, the equation for the total amount of raisin and almond is given as,

r + a = 5

And, for the cost of the 5 pound bag it is given as,

3r + 6a = 20

Hence, the equations to justify the given case are r + a = 5 and 3r + 6a = 20 respectively.

To know more about system of equations click on,

brainly.com/question/24065247

#SPJ2

Answer:

\(\$1583.33\)

Step-by-step explanation:

Let \(d\) be the amount of money you need to save each month to have the full $23,000.

We can write the following inequality:

\(4,000+12d\geq 23,000\)

Solving for \(d\):

\(4,000+12d\geq 23,000,\\12d\geq 19,000\\d\geq \approx \boxed{\$1583.33}\)

Answer:

8

Step-by-step explanation:

Total length of the fabric is \(6\dfrac{2}{3}=\dfrac{20}{3}\ \text{yards}\)

We need to find the number of scarves can she make if she needs 5/6 of a yard for each scarf.

Let she needs x scarves. So, ATQ

\(x\times \dfrac{5}{6}=\dfrac{20}{3}\\\\x=\dfrac{20}{3}\cdot\dfrac{6}{5}\\\\x=8\)

Hence, she can make 8 scarves.

Answer:

8

Step-by-step explanation:

the guy above me explained