a grid of a hundred square show 7 shaded squares what decimal number is represented
Answers
Answer:
0.07
Step-by-step explanation:
From the question, a given grid was divided into a definite number of squares with some of the squares shaded.
Total number of squares in the grid = 100
number of shaded squares in the grid = 7
Thus, 7 squares are shaded out of 100 square in the grid.
So that this can be expressed in fraction as;
\(\frac{number of shaded squares}{total number of squares}\) = \(\frac{7}{100}\)
= 0.07
The decimal number of the squares represented is 0.07.
Related Questions
Need ANSWER ASAP
Consider the following transformed function
y = −2 Sin [2( − 45°)] + 1
a) Graph the five key points of Parent function on the provided grid.
b) State the following for the transformed function
Amplitude=
period=
Horizontal Phase shift =
Equation of axis=
c) Graph at least two cycles of the transformed function by transforming the key points of the parent function. (Don’t forget to label the x-axis and y -axis)
Answers
Answer:
See explanation below.
Step-by-step explanation:
Given transformed function:
\(y=-2 \sin \left[2(x-45^{\circ})\right]+1\)
Part (a)The parent function of the given function is: y = sin(x)
The five key points for graphing the parent function are:
3 x-intercepts → (0°, 0) (180°, 0) (360°, 0)maximum point → (90°, 1)minimum point → (270°, -1)(See attachment 1)
Part (b)Standard form of a sine function:
\(\text{f}(x)=\text{A} \sin\left[\text{B}(x+\text{C})\right]+\text{D}\)
where:
A = amplitude (height from the mid-line to the peak)2π/B = period (horizontal distance between consecutive peaks)C = phase shift (horizontal shift - positive is to the left)D = vertical shift (axis of symmetry: y = D)Therefore, for the given transformed function:
\(y=-2 \sin \left[2(x-45^{\circ})\right]+1\)
Amplitude = -2Period = 2π/2 = πPhase shift = 45° to the rightEquation of axis of symmetry: y = 1Part (c)See attachment 2.
![Need ANSWER ASAPConsider the following transformed functiony = 2 Sin [2( 45)] + 1a) Graph the five key](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/rHmvQCSFzLuN7xkVIxhNC3hToKfYa2ZX.png)
![Need ANSWER ASAPConsider the following transformed functiony = 2 Sin [2( 45)] + 1a) Graph the five key](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/RTeQ1nKnPwOJZpxZH6e5ecn6PqRfr3g0.png)
Can someone help me with
this I am very confused.

Answers
The probability of the all elements in universal set that is not in A, that is, P(A¹) = 1/3
How to calculate the probability of the given event?To determine the probability of all the elements in universal set that is not in A, the formula that should be used is given as follows;
Probability = possible outcome/sample space
The sample space = 3/3 = 1
The possible outcome (A¹) = 1-⅔
= 1/3
The probability of A¹ = 1/3÷1 = 1/3
Learn more about probability here:
https://brainly.com/question/31123570
#SPJ1
A box of nails weighs 42 5/8 pounds. If you used 4 3/16 pounds of nails yesterday and another 6 1/4 pounds
today, how many pounds of nails are left?
Answers
The fraction for the nails that remain is 32 3/16 pounds.
What is a fraction?A fraction is simply a piece of a whole. The number is represented mathematically as a quotient where the numerator and denominator are split. In a simple fraction, the numerator as well as the denominator are both integers.
In this case, the box of nails weighs 42 5/8 pounds and you used 4 3/16 pounds of nails and another 6 1/4 pounds.
The nails left will be:
= Total nails - Nails used
= 42 5/8 - (4 3/16 + 6 1/4)
= 42 5/8 - 10 7/16
= 32 3/16
Learn more about fractions on:
brainly.com/question/17220365
#SPJ1
Find the area of the shaded portion in the equilateral triangle with sides 6. Show all work for full credit.
(Hint: Assume that the central point of each arc is its corresponding vertex.)
Answers
The area of the shaded portion in the equilateral triangle with sides 6 is 9√3 - 36π.
To find the area of the shaded portion in the equilateral triangle, we need to determine the area of the three arcs and subtract it from the area of the equilateral triangle.
First, let's find the area of one arc. Each arc has a radius equal to the length of the side of the equilateral triangle, which is 6. The formula for the area of a sector is A = (θ/360)πr², where θ is the central angle in degrees.
In an equilateral triangle, each interior angle measures 60 degrees, so the central angle of the arc is 120 degrees (360 degrees divided by 3). Plugging these values into the formula, we get A_arc = (120/360)π(6)² = (1/3)π(6)² = 12π.
Since there are three identical arcs, the total area of the arcs is 3 times the area of one arc, which is 3(12π) = 36π.
Now, let's find the area of the equilateral triangle. The formula for the area of an equilateral triangle is A_triangle = (√3/4)s², where s is the length of a side.
Plugging in the value of the side length, we have A_triangle = (√3/4)(6)² = (√3/4)(36) = 9√3.
Finally, we subtract the area of the arcs from the area of the equilateral triangle to find the shaded portion's area: A_shaded = A_triangle - A_arc = 9√3 - 36π.
For more such questions on triangle
https://brainly.com/question/1058720
#SPJ8
y = 3x + 2
y = 2x + 2
One solution
No solution
Infinite solutions
Answers
Answer:
The answer would be One solution.
Step-by-step explanation:
Solving by substitution.y=3x+2;y=2x+2
Step: Solve y=3x+2 for y:
y=3x+2
Step: Substitute 3x+2 for y in y=2x+2:
y=2x+2
3x+2=2x+2
3x+2+−2x=2x+2+−2x(Add -2x to both sides)
x+2=2
x+2+−2=2+−2(Add -2 to both sides)
x=0
Step: Substitute 0 for x in y=3x+2:
y=3x+2
y=(3)(0)+2
y=2(Simplify both sides of the equation)
Answer:
x=0 and y=2
If it was no solution you would not be able to solve. If it was infinite then there would be infinite solutions, but there is not so One Solution is the answer.
Please explain your answer to the question in the picture with steps

Answers
Answer:
x = 31.2
Step-by-step explanation:
You want the solution to the proportion 12/x = 5/13.
Rational equationYou can eliminate the fractions by multiplying this equation by the least common denominator. That value is 13x, the product of these denominators. Multiplying by 13x, we have ...
\(\dfrac{12}{x}\times13x=\dfrac{5}{13}\times13x\\\\\\12\cdot13=5\cdot x\qquad\text{simplified}\)
Now, the value of x is found by dividing both sides by its coefficient.
\(\dfrac{12\cdot13}{5}=\dfrac{5x}{5}\\\\\\\dfrac{156}{5}=x\\\\\boxed{31.2=x}\)
__
Additional comment
The first step we did, multiplying by 13x, is also sometimes called "cross multiplication." The result of that step is that each numerator is multiplied by the opposite denominator.
Multiplying both sides of the equation by the same value (13x) is supported by the multiplication property of equality. The term "cross multiplication" is descriptive of the result, but is not a recognized property of equality. It is a good idea to keep the math operations you do grounded in the properties of equality.
You will notice that the steps we did were "multiply by 13x" and "divide by 5". These can be done at once by "multiply by 13x/5". Of course, that operation is done to both sides of the equation.
Any proportion can be written 4 ways:
\(\dfrac{12}{x}=\dfrac{5}{13}\qquad\dfrac{x}{12}=\dfrac{13}{5}\qquad\dfrac{x}{13}=\dfrac{12}{5}\qquad\dfrac{13}{x}=\dfrac{5}{12}\)
These can be thought of as "upside down" and "sideways." We like the versions with the variable on top of a fraction, because the solution to that is simply multiplication by the variable's denominator.
<95141404393>
Question 1 of 10
What is the approximate distance between the points (-3,-4) and (-8, 1) on a
coordinate grid?
O A. 11.40 units
OB. 12.08 units
O C. 7.07 units
D. 3.16 units
Answers
Answer:
Step-by-step explanation:
Answer:
the approximate distance between the points is
√25+25 = 5√2
=7.07
Step-by-step explanation:
Five less than twice the value of a number is equal to three times the quantity of 4 more than 1/2 the number what is the number let x be the number right and solve an equation to find x show your work.
Answers
The value of the number is x = 34.
Let's break down the problem and solve it step by step.
1. "Five less than twice the value of a number": This can be represented as 2x - 5, where x is the number.
2. "Three times the quantity of 4 more than 1/2 the number": This can be represented as 3 * (x/2 + 4).
According to the problem statement, the two expressions are equal. We can set up the equation as follows:
2x - 5 = 3 * (x/2 + 4)
Now, let's solve the equation:
2x - 5 = 3 * (x/2 + 4)
Distribute the 3 to both terms inside the parentheses:
2x - 5 = (3/2)x + 12
Multiply through by 2 to eliminate the fraction:
2(2x - 5) = 2((3/2)x + 12)
4x - 10 = 3x + 24
Next, let's isolate the x term by moving the constant terms to the other side of the equation:
4x - 3x = 24 + 10
Simplify:
x = 34
For more such questions on number,click on
https://brainly.com/question/24644930
#SPJ8
complete solutions manual a first course in differential equations with modeling applications ninth edition differential equations with boundary-vary problems tenth edition
Answers
A first course in differential equations with modeling applications ninth edition is a textbook that covers the basics of differential equations and their applications in mathematical modeling.
It begins with an introduction to the concepts of differential equations, including the definition, solution methods, and the concept of modeling. It then covers topics such as first-order linear equations, higher-order linear equations, systems of linear differential equations, and nonlinear equations. It also has a chapter on boundary-value problems, which is a type of differential equation that involves a set of boundary conditions that must be satisfied for the solution to be valid.
In order to solve differential equations with boundary-value problems, we must first define the boundary conditions that must be satisfied for the solution to be valid. This involves setting up the boundary conditions in terms of the dependent and independent variables of the equation. We then solve the equation using the boundary conditions and the equation itself. The solution is then used to calculate values for the independent and dependent variables at the boundary points. Finally, we can verify the solution by substituting the calculated values into the equation and seeing if the solution is valid.
Learn more about differential equations here:
https://brainly.com/question/14620493
#SPJ4
Workout (10-3x2)^2
Please help with both questions

Answers
Answer:
b) 16 c)a=-3
Step-by-step explanation:
b) (10-3x2)^2 = (4)^2 = 16
c) (5)^-3 = 1/125
What is the sum of 2 and 3 subtracted from the product of 2 and the difference of 7 and 4? The answer is 1, but how is it solved?
Answers
Answer: -1
Step-by-step explanation:
sum of 2 and 3 subtracted from the product of 2 difference of 7 and 4
(2+3) - 2 ( 7 - 4 ) = -1
(2+3)-2(7-4) =
5 - 2(3) =
5-6 = -1
The sum of 2 and 3 subtracted from the product of 2 and the difference of 7 and 4 is equivalent to 1.
What is Equation Modelling?Equation modelling is the process of writing a mathematical verbal expression in the form of a mathematical expression for correct analysis, observations and results of the given problem.
We have the sum of 2 and 3 subtracted from the product of 2 and the difference of 7 and 4
From the question, we can model the equation as -
x = 2 × (7 - 4) - (2 + 3)
x = 2(3) - 5
x = 6 - 5
x = 1
Therefore, the sum of 2 and 3 subtracted from the product of 2 and the difference of 7 and 4 is equivalent to 1.
To solve more questions on Equation Modelling, visit the link below -
brainly.com/question/14441381
#SPJ2
Josiah can jog 5/6 mile in 15 minutes. What’s the average speed in miles per hour?
Answers
0.83 x 4= 3.32
If he runs 0.83 miles every 15 minutes you’ll multiply by 4 to make an hour.
Ty bought a new computer for $499. This brand depreciates at a rate of 12% of the original price per year. The value y of Ty's computer, x years after he purchased it, is found using an equation in the form y = mx + b. What is the approximate value of m?
Answers
Answer:
the approximate value of m is -0.12, indicating that the value of Ty's computer decreases by 0.12 (or 12%) each year.
Step-by-step explanation:
o express this depreciation rate as a slope in the equation y = mx + b, we need to determine how much the value changes (the "rise") for each year (the "run").
Since the value decreases by 12% per year, the slope (m) would be -12%. However, we need to express the slope as a decimal, so we divide -12% by 100 to convert it to a decimal:
m = -12% / 100 = -0.12
Please help with this!!! Multiply 6x5 7/8
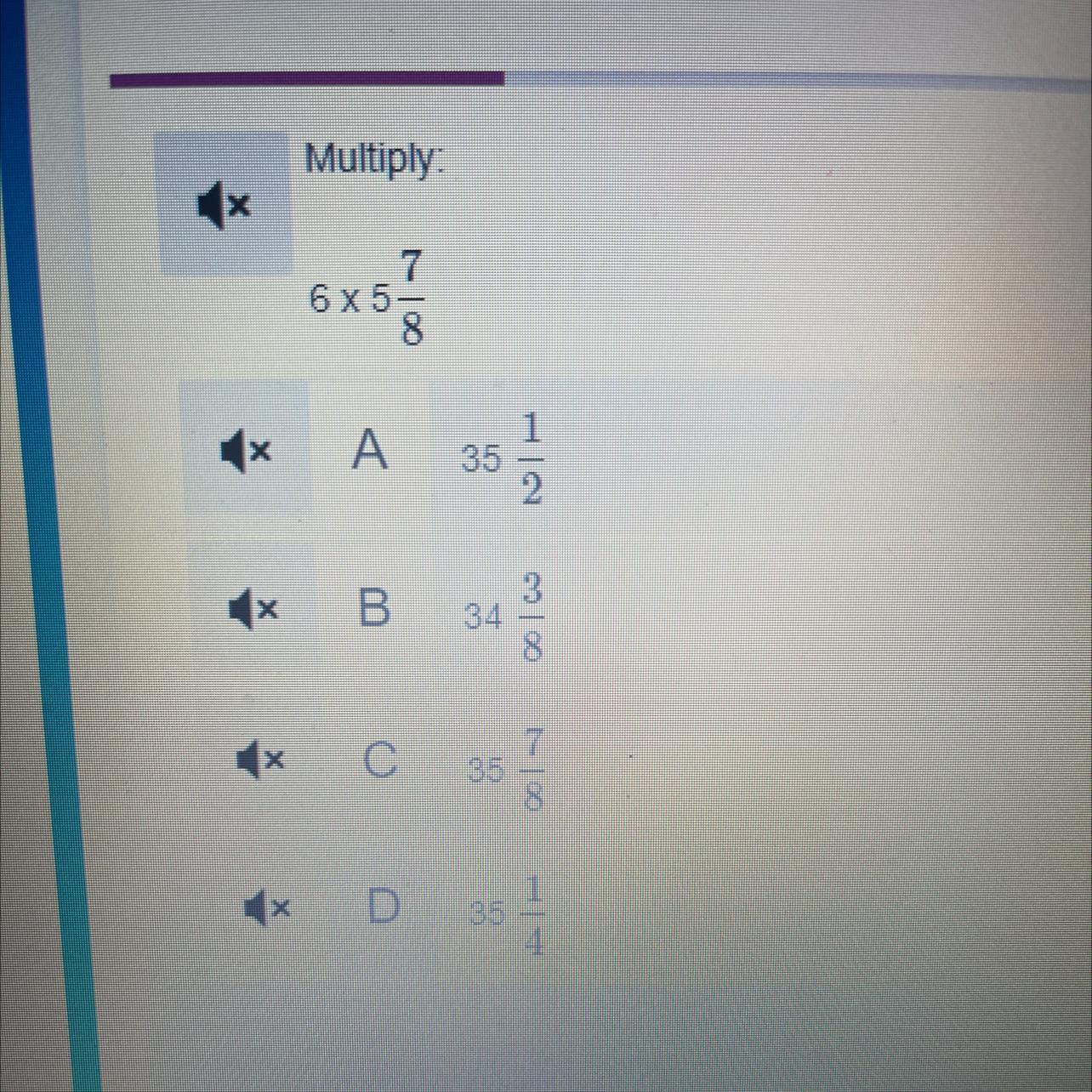
Answers
Answer:
35 and 1/4
Step-by-step explanation:
6x47/8
6/1x47/8
282/8
35 1/4 or 35.25
how do i go about finding x° and ycm, please?
I've tried Sine Rule & Cosine Rule... I thought i had done it correctly until i worked out the angles added up to much higher than 180° so it cannot be correct... can anyone help?

Answers
From the solution;
x = 62.62°
y = 8.9 cm
What is the sine rule?The sine rule (also known as the law of sines) is a mathematical formula that relates the sides and angles of a triangle. Specifically, it relates the ratios of the lengths of the sides of a triangle to the sine of the opposite angles.
By the use of the sine rule;
a/Sin A = c/Sin C
Sin C = cSin A/a
C = Sin-1(cSin A/a)
C = Sin-1(7.8 * sin 66.4/9.2)
C = 50.98°
B = 180 - (50.98° + 66.4)
B = 62.62°
Then;
a/Sin A = b/Sin B
9.2/Sin66.4 = b/Sin 62.62
b = 9.2 * Sin 62.62/Sin66.4
b = 9.2 * 0.89/0.92
b = 8.9 cm
Learn more about sine rule:https://brainly.com/question/30339234
#SPJ1
Meryl pays £400 into her sister's South African bank account. How much money did her sister receive if the current exchange rate is £1 = R19,29?
Answers
The price of one currency in respect to another is referred to as its exchange rate.
What is meant by current exchange rate?An exchange rate in the world of finance is the price at which one currency will be exchanged for another. The majority of the time, currencies are national ones, but they can also be supra-national ones like the euro or sub-national ones like Hong Kong.
A currency's price in relation to another is known as its exchange rate. You can have fixed or fluctuating exchange rates. While a country's central bank controls fixed exchange rates, the process of supply and demand on the open market controls floating exchange rates.
The rate at which one currency can be exchanged for another between countries or economic zones is known as the exchange rate. It is crucial in assessing trade and capital movement dynamics and is used to calculate the value of various currencies in respect to one another.
Convert the currency:
£ 400 × R 19.29/£2 = R 7,716
To learn more about exchange rate refer to:
https://brainly.com/question/6675565
#SPJ1
An equation is shown below: 5(3x − 15) + 16 = 5x + 11 Part A: Write the steps you will use to solve the equation, and explain each step. (8 points) Part B: What value of x makes the equation true? (2 points)
Answers
The result of the unknown variable x is equivalent to 7
Solving linear equationsLinear equations are equation that has a leading degree of 1. Given the expression below:
5(3x − 15) + 16 = 5x + 11
Expand the expression
5(3x) - 5(15) + 16 = 5x + 11
15x - 75 + 16 = 5x + 11
15x - 5x - 59 - 11 = 0
10x - 70 = 0
10x = 70
Divide both sides by 10
10x/10 = 70/10
x = 7
Hence the value of x makes the equation true is 7
Learn more on linear equation here: https://brainly.com/question/2030026
#SPJ1
WILL GIVE BRAINLIEST
(x-2)(y-3)=0
with diagram plz
Answers
Answer:
x=2,y=3
Step-by-step explanation:
x-2=0
x=2
y-3=0
y=3
What is this it’s hard to understand

Answers
For a rotation of 180° clockwise or counterclockwise, the x and y will always be the opposite. For instance, if coordinates (4, 7) are being 180° rotated, the new set of coordinates will be (-4, -7).
Remembering the rule, the final answer to your question is A, 180° clockwise rotation about the origin.
4) Ms Smith has a garden that is 16 feet by 12 feet. She wants to put a walkway along each diagonal.
How many feet of walkway will she need?
Answers
In the given problem, using Pythagorean theorem, if Ms. Smith wants to put a walkway along each diagonal, she will need a total of 40 feet of walkway.
How to Solve the problem?To find the length of the walkway, we need to find the length of the diagonals of the garden. We can use the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides.
In this case, the two sides of the rectangle are 16 feet and 12 feet. So, we can find the length of the two diagonals as follows:
The first diagonal: 16² + 12² = 256 + 144 = 400. Taking the square root of both sides gives us: √400 = 20 feet.The second diagonal (which is the same length as the first): 20 feet.Ms. Smith wants to put a walkway along each diagonal, so she will need a total of 20 + 20 = 40 feet of walkway.
Learn more about Pythagorean theorem here: https://brainly.com/question/343682
#SPJ1
A random sample of 10 parking meters in a resort community showed the following incomes for a day. Assume the incomes are normally distributed. (a) Find the 95% confidence interval for the true mean and interpret the result. Round to the nearest cent. (b) Find margin of error. $3.60 $4.50 $2.80 $6.30 $2.60 $5.20 $6.75 $4.25 $8.00 $3.00
Answers
Answer:
A 95% confidence interval for the true mean is [$3.39, $6.01].
Step-by-step explanation:
We are given that a random sample of 10 parking meters in a resort community showed the following incomes for a day;
Incomes (X): $3.60, $4.50, $2.80, $6.30, $2.60, $5.20, $6.75, $4.25, $8.00, $3.00.
Firstly, the pivotal quantity for finding the confidence interval for the population mean is given by;
P.Q. = \(\frac{\bar X-\mu}{\frac{s}{\sqrt{n} } }\) ~ \(t_n_-_1\)
where, \(\bar X\) = sample mean income = \(\frac{\sum X}{n}\) = $4.70
s = sample standard deviation = \(\sqrt{\frac{\sum (X-\bar X)^{2} }{n-1} }\) = $1.83
n = sample of parking meters = 10
\(\mu\) = population mean
Here for constructing a 95% confidence interval we have used a One-sample t-test statistics because we don't know about population standard deviation.
So, 95% confidence interval for the population mean, \(\mu\) is ;
P(-2.262 < \(t_9\) < 2.262) = 0.95 {As the critical value of t at 9 degrees of
freedom are -2.262 & 2.262 with P = 2.5%}
P(-2.262 < \(\frac{\bar X-\mu}{\frac{s}{\sqrt{n} } }\) < 2.262) = 0.95
P( \(-2.262 \times {\frac{s}{\sqrt{n} } }\) < \({\bar X-\mu\) < \(2.262 \times {\frac{s}{\sqrt{n} } }\) ) = 0.95
P( \(\bar X-2.262 \times {\frac{s}{\sqrt{n} } }\) < \(\mu\) < \(\bar X+2.262 \times {\frac{s}{\sqrt{n} } }\) ) = 0.95
95% confidence interval for \(\mu\) = [ \(\bar X-2.262 \times {\frac{s}{\sqrt{n} } }\) , \(\bar X+2.262 \times {\frac{s}{\sqrt{n} } }\) ]
= [ \(4.70-2.262 \times {\frac{1.83}{\sqrt{10} } }\) , \(4.70+ 2.262 \times {\frac{1.83}{\sqrt{10} } }\) ]
= [$3.39, $6.01]
Therefore, a 95% confidence interval for the true mean is [$3.39, $6.01].
The interpretation of the above result is that we are 95% confident that the true mean will lie between incomes of $3.39 and $6.01.
Also, the margin of error = \(2.262 \times {\frac{s}{\sqrt{n} } }\)
= \(2.262 \times {\frac{1.83}{\sqrt{10} } }\) = 1.31
Using the t-distribution, it is found that:
a) The 95% confidence interval for the true mean is (3.39, 6.01). It means that we are 95% sure that the true mean income for all parking meters in the resort community from which the sample was taken is between these two values.
b) The margin of error is of $1.31.
Item a:
We will have the standard deviation for the sample, which is why the t-distribution is used to solve this question.
The sample size given is of \(n = 10\), and using a calculator, it is found that:
The sample mean of \(\overline{x} = 4.7\).
The sample standard deviation of \(s = 1.833\).
The confidence interval is:
\(\overline{x} \pm t\frac{s}{\sqrt{n}}\)
The critical value, using a t-distribution calculator, for a two-tailed 95% confidence interval, with 10 - 1 = 9 df, is t = 2.2622.
Then, the interval is:
\(\overline{x} - t\frac{s}{\sqrt{n}} = 4.7 - 2.2622\frac{1.833}{\sqrt{10}} = 3.39\)
\(\overline{x} + t\frac{s}{\sqrt{n}} = 4.7 + 2.2622\frac{1.833}{\sqrt{10}} = 6.01\)
The 95% confidence interval for the true mean is (3.39, 6.01). It means that we are 95% sure that the true mean income for all parking meters in the resort community from which the sample was taken is between these two values.
Item b:
The margin of error is half the distance between the two bounds, hence:
\(M = \frac{6.01 - 3.39}{2} = 1.31\)
A similar problem is given at https://brainly.com/question/22596713
write the slope intercept 5x+7y=21
Answers
Answer:
slope = - 5/7
y intercept = 3
Step-by-step explanation:
26 x (-48) + (-48) x (-36) pls tell the answer
Answers
-1248 -1248 -. 936
- 3432
-1248 + 1728
480
At the grocery store, Mr. Abroms saw eggplants that cost $1.79 each, apples that cost $0.59 each, bags of spinach that cost $2.55 each, and cartons of orange juice that cost $3.89 each. Which of these statements below are true? Choose the three correct answers.

Answers
Answer:
Option 1, 3 and 5 are correct
Step-by-step explanation:
Given
Eggplants = $1.79 each
Apples = $0.59 each,
Bags of spinach = $2.55 each
Cartons of orange juice = $3.89 each
Required
Select three true statements
To do this, we'll check the options one after the other
1. 4 eggplants cost about $0.50 less than 3 bags of spinach
First, we need to calculate the cost of 4 eggplants
4 Eggplants = 4 * 1 Eggplants
4 Eggplants = 4 * $1.79
4 Eggplants = $7.16
Next, we calculate the cost of 3 bags of Spinach
3 bags of Spinach = 3 * 1 bag of Spinach
3 bags of Spinach = 3 * $2.55
3 bags of Spinach = $7.65
Determine the difference
Difference = |Eggplants - Bags of Spinach|
Difference = |$7.16 - $7.65|
Difference = |-$0.49|
Difference = $0.49
This statement is true because $0.49 approximates to $0.50
2. Total cost of 4 apples and 2 eggplants $0.50 is more than $6.00
First, we need to calculate the cost of 4 apples
4 Apples = 4 * 1 Apples
4 Apples = 4 * $0.59
4 Apples = $2.36
Next, we calculate the cost of 2 Eggplants
2 Eggplants = 2 * 1 Eggplant
2 Eggplants = 2 * $1.79
2 Eggplants = $3.58
Add this two results together
Total = 4 Apples + 2 Eggplants
Total = $2.36 + $3.58
Total = $5.94
This statement is false because the sum is less than $6.00
3. Total cost of 4 eggplants, 4 apples and 1 carton of orange juice is $13.41
In (1) & (2) above
4 Eggplants = $7.16
4 Apples = $2.36
1 carton of orange juice = $3.89
Add the above together
Total = $7.16 + $2.36 + $3.89
Total = $13.41
This statement is true because the sum is $13.41
4. Total cost of 5 eggplants is greater than cost of 4 bags of spinach
First, we need to calculate the cost of 5 eggplants
5 Eggplants = 5 * 1 Eggplants
5 Eggplants = 5 * $1.79
5 Eggplants = $8.95
Next, we calculate the cost of 4 bags of Spinach
4 bags of Spinach = 4 * 1 bag of Spinach
4 bags of Spinach = 4 * $2.55
4 bags of Spinach = $10.20
This statement is false because 4 Eggplants costs less than $ bags of spinach
5. Total cost of 2 eggplants, 2 apples and 2 cartons of orange juice is $9.99 more than cost of 1 bag of spinach
From (2) above
2 Eggplants = $3.58
Next, we need to calculate the cost of 2 apples
2 Apples = 2 * 1 Apples
2 Apples = 2 * $0.59
2 Apples = $1.18
Next, we need to calculate the cost of 2 cartons of orange juice
2 Cartons = 2 * 1 Carton
2 Apples = 2 * $3.89
2 Apples = $7.78
Sum these up
Total = $3.58 + $1.18 + $7.78
Total = $12.54
1 Bag of spinach = $2.55 each
Subtract 1 Bag of spinach from the $12.54
Difference = $12.54 - $2.55
Difference = $9.99
This statement is true because the difference is $9.99
What is the integral expression for the volume of the solid formed by revolving the region bounded by the graphs of y = x2 - 3x and y = x about the horizontal line y = 6? * 18 (6 - x2 + 3x)2-(6- x)?dx o Tejo (6-x2+3x)2 - (6 - x)?dx OTS (6 - 12 - (6 - x2 + 3xPdx Orla (6 - XP2 – (6-x2 + 3x)
Answers
The integral expression for the volume of the solid formed by revolving the region bounded by the graphs of y = x₂ - 3x and y = x about the horizontal line y = 6 is 2πx(6 - x² + 3x)dx, which is integrated from x=0 to x=3, which gives us 81π/2.
To find the integral expression for the volume of the solid formed by revolving the region bounded by the graphs of y=x² - 3x and y=x about the horizontal line y=6, we can use the method of cylindrical shells.
First, we need to find the limits of integration, The graphs of y = x² - 3x and y=x intersect at x=0 and x=3. Therefore, we integrate from x=0 to x=3.
Next, we consider a vertical strip of width dx at a distance x from the y- boxes. the height of the strip is the difference between the height of the curve y= x² - 3x and the line y=6, which is 6 - (x² - 3x) = 6 - x² + 3x. the circumference of the shell is 2π times the distance x from the y-axis, and the thickness of the shell is dx. the volume of the shell is the product of the height, circumference, and thickness which is
dV = 2πx(6 - x² + 3x)dx
To find the total volume, we integrate this expression from x=0 to x=3.
V = ∫₀³ 2πx(6 - x² + 3x)dx, after simplifying the integrand we get :
V = 2π ∫₀³ (6x - x³ + 3x²)dx, integrating term by term we get :
V = 2π [(3x²/2) - (x⁴/4) + (x^3)] from 0 to 3, now evaluation at the limits of integration we get:
V = 2π [(3(3)²/2) - ((3)⁴/4) + (3)³] - 2π [(0)^2/2 - ((0)⁴/4) + (0)^3]= 2π [(27/2) - (27/4) + 27] - 0 = 81π/2
To know more about cylindrical shells refer to the link brainly.com/question/2263921
#SPJ4
What is the coefficient in the expression?
10 – 6 + 5n
Answers
The coefficient in the expression is 5.
How to find the coefficient in an algebraic expression?A coefficient is a numerical value that is multiplied by a variable in an algebraic expression.
In a polynomial expression, coefficients can be the numbers in front of the variables. The coefficient determines the size and direction of the variable's effect on the expression as a whole. For example, in the expression 2x, the coefficient is 2.
Therefore, the coefficient in the expression 10 – 6 + 5n is 5.
Learn more about algebraic expression on:
brainly.com/question/4344214
#SPJ1
Answer: 5
Step-by-step explanation:
Jose May 20% off of his free throws over the season if he shot a 180 free throws how many did he make
Answers
Answer:
He made 36 free throws out of 180
is it possible for an object to have no (zero) momentum? use the mathematical definition of momentum (p
Answers
Yes, it is possible for an object to have zero momentum. Momentum is defined as function the product of mass and velocity, so an object with zero mass or zero velocity will have zero momentum.
Momentum is a physical property of an object that is equal to the product of its mass and velocity. It is measured in kilogram meters per second (kg m/s) and is a vector quantity, meaning it has both magnitude and direction. In order for an object to have zero momentum, it must have either zero mass or zero velocity. An object with zero mass will always have zero momentum regardless of its velocity, while an object with zero velocity will only have zero momentum if its mass is also zero. An object with nonzero mass but zero velocity still has nonzero momentum if its mass is not zero. Therefore, it is possible for an object to have zero momentum.
Learn more about function here
https://brainly.com/question/29633660
#SPJ4
the complete question is
is it possible for an object to have no (zero) momentum? use the mathematical definition of momentum (p) to explain
It is possible for an object to have No (Zero) momentum because Momentum is the product of mass and velocity, so the object with zero mass or zero velocity will have No momentum.
What is Momentum ?
The Momentum of an object is a vector quantity that is defined as the product of the mass and velocity , the unit of measurement if Kg m/s .
So , for the object to have No (zero) momentum, the object must have either zero mass or zero velocity. that means the object with zero mass will always have No (zero) momentum regardless of velocity of the object ,
whereas the object with 0 velocity will only have No (zero) momentum if the mass is also 0 .
Therefore , By the Mathematical Definition of momentum , Yes , it is possible for the object to have No(zero) momentum .
Learn more about Momentum here
https://brainly.com/question/8635369
#SPJ4
What is (-4)x(-6)= that’s it
Answers
Answer:
24
Step-by-step explanation:
the negatives cancel each other out
Bennett Griffin and Chula Garza organized Cole Valley Book Store as a corporation; each contributed $71,500 cash to start the business and received 5,600 shares of common stock. The store completed its first year of operations on December 31, current year. On that date, the following financial items for the year were determined: December 31, current year, cash on hand and in the bank, $69,250; December 31, current year, amounts due from customers from sales of books, $43,500; unused portion of store and office equipment, $72,500; December 31, current year, amounts owed to publishers for books purchased, $12,400; one-year note payable to a local bank for $3,200. No dividends were declared or paid to the stockholders during the year.
Required:
Complete the following balance sheet as of the end of the current year. Some information has been given below.
What was the amount of net income for the year? (Hint: Use the retained earnings equation [Beginning Retained Earnings + Net Income − Dividends = Ending Retained Earnings] to solve for net income.)
Answers
he net income for the year is $16,550.
Calculation of the net income for the year:Retained earnings equation is:Beginning Retained Earnings + Net Income − Dividends = Ending Retained EarningsWhere, Beginning Retained Earnings = $0 (not given)Ending Retained Earnings = $16,550 (calculated from balance sheet)Dividends = $0 (not given)
Therefore,Net Income = Ending Retained Earnings - Beginning Retained Earnings + Dividends= $16,550 - $0 + $0= $16,550 Balance Sheet of Cole Valley Book Store as of December 31, current year:Current assets Cash on hand and in bank = $69,250 Amounts due from customers from sales of books = $43,500 Total current assets = $112,750 Property, plant, and equipment Unused portion of store and office equipment = $72,500
Total assets = $185,250Liabilities Amounts owed to publishers for books purchased = $12,400 One-year note payable to a local bank = $3,200 Total liabilities = $15,600 Stock holders' Equity Common stock, 5,600 shares at $71,500 = $400,400 Retained earnings, beginning = $0Net income = $16,550 Retained earnings, ending = $16,550 Total stockholders' equity = $416,950Total liabilities and stockholders' equity = $185,250 + $15,600 + $416,950= $617,800
for more search question income
https://brainly.com/question/30157678
#SPJ8