A hawk was flying at an elevation of 215 feet, looking for new hunting ground. It rose 95 feet as it continued to search.
What is the elevation of the hawk now?
Answers
Answer:
310 feet
Step-by-step explanation:
215 + 95 = 310
:)
Answer:
its 310
Step-by-step explanation:
Related Questions
Plz help due tomorrow

Answers
Answer:
You have to do Divison.
Step-by-step explanation:
Hope this can help you!
Point D has coordinates (4, 1). What are the coordinates of Rx = 2(D)?
Answers
Answer:
The coordinates of Rₓ = \(2^{(D)}\) = D'(0, 1)
Step-by-step explanation:
As given, D = (4, 1)
Now,
The coordinates of Rₓ = \(2^{(D)}\) = D'(0, 1)
You are planning to grow a garden. The store offers seeds for 11 different kinds of vegetables. You decide to get 7 seed packets (one for each of 7 different kinds of vegetables) at this store. How many ways can you make this selection
Answers
There are 330 ways to select 7 seed packets out of 11.
How to count the number of ways to select 7 seed packets out of 11?To count the number of ways to select 7 seed packets out of 11, we can use the combination formula:
\(( \frac {k}n )= k!(n-k)!n!\)
where n is the number of items to choose from, and k is the number of items to choose. In this case, n=11 and k=7.
Plugging these values into the formula, we get:
\(( \frac{7}{11})= 7!(11-7)!11!\)
Simplifying the factorials, we get:
\(( \frac{7}{11})= \frac{7\times 6\times 5\times 4\times 3\times 2\times 1}{11\times 10\times 9\times 8\times 7\times 6\times 5}\)
Simplifying further, we get:
\(( \frac{7}{11} )= \frac{4\times 3\times 2\times 1}{11\times 10\times 9\times 8}\)
Simplifying again, we get:
\((\frac{11}7)=330\)
Therefore, there are 330 ways to select 7 seed packets out of 11.
Learn more about combination formula
brainly.com/question/14685054
#SPJ11
a. What is the probability that a randomly selected survey participant prefers the NFL? 0.5286 (Round to four decimal places as needed.) b. What is the probability that a randomly selected survey participant has a college degree and prefers the NBA? (Round to four decimal places as needed.) a. Of two customers selected, what is the probability that both will be on a business trip? 0.1719 (Round to four decimal places as needed.) b. What is the probability that a customer will be on a business trip or will experience a hotel problem during a stay at the hotel? (Round to four decimal places as needed.)
Answers
a. The probability that a randomly selected survey participant prefers the NFL is given as 0.5286. This means that out of all the participants in the survey, approximately 52.86% indicated a preference for the NFL.
b. To determine the probability that a randomly selected survey participant has a college degree and prefers the NBA, we would need additional information about the joint probability of these events. Without that information, we cannot calculate the exact probability.
a. To find the probability that both of two randomly selected customers will be on a business trip, we need to know the individual probabilities of each customer being on a business trip and assume that their trips are independent. If the probability of customer A being on a business trip is denoted as P(A) and the probability of customer B being on a business trip is denoted as P(B), then the probability of both being on a business trip is given by P(A and B) = P(A) * P(B). The given probability of 0.1719 may represent this joint probability.
b. The probability that a customer will be on a business trip or will experience a hotel problem during a stay at the hotel can be determined by summing the individual probabilities of these events. Let's denote the probability of being on a business trip as P(B) and the probability of experiencing a hotel problem as P(H). Then, the probability of either event occurring can be calculated as P(B or H) = P(B) + P(H) - P(B and H), assuming that the events are mutually exclusive. However, the specific values of P(B), P(H), and P(B and H) are needed to compute the exact probability.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
A local hamburger shop sold a combined total of 817 hamburgers and cheeseburgers on Friday. There were 67 more cheeseburgers sold than hamburgers. How
many hamburgers were sold on Friday?
hamburgers
Answers
The number of hamburgers sold on Friday was 442.
Let us form the linear equation to find the number of burgers;
Let the cheeseburger be represented by x.
Since there were 67 more cheeseburgers sold than hamburgers. This means that hamburgers will be:
The number of hamburgers = x + 67.
Since the local hamburger shop sold a combined total of 817 hamburgers and cheeseburgers. This will be:
x + x + 67 = 817
2x + 67= 817
2x = 817 - 67
2x = 750
x = 750 / 2
x = 375
So, 375 cheeseburgers were sold on Friday.
Therefore, the number of hamburgers sold will be:
= 817 - 375
= 442
Thus, the number of hamburgers sold on Friday was 442.
To learn more about the linear equation visit:
https://brainly.com/question/13738061
#SPJ9
Help pls. just area :(

Answers
Area of top right rectangle
8(7.5)60ft²Area of left top rectangle
10(7.5)75ft²Area of horizontal rectangle
(20-7.5)(45)12.5(45)562.5ft²Total
562.5+75+60562.5+135697.5ft²
Answer:
B) 697.5 ft²
Step-by-step explanation:
The quickest way to approach this question is to calculate the area of the entire rectangle, then subtract the area of the small rectangle (the rectangle missing at the top).
Formula
Area of a rectangle = width x length
⇒ Area of large rectangle = 20 ft x 45 ft
= 900 ft²
⇒ Area of small rectangle = 7.5 ft x (45 - 8 - 10) ft
= 7.5 ft x 27 ft
= 202.5 ft²
⇒ Area of the pool cover = large rectangle - small rectangle
= 900 ft² - 202.5 ft²
= 697.5 ft²
As one equation:
Area of pool cover = (20 x 45) - (7.5 x (45 - 8 - 10))
= 900 - (7.5 x 27)
= 900 - 202.5
= 697.5 ft²
Help y’all
Given the circle O and PR is the diameter, so m
Answers
The measure of angle PQR is 90 degrees.
What is the measure of angle PQR in a circle O with diameter PR?Since PR is the diameter of the circle, it follows that angle POR is a right angle, i.e., it measures 90 degrees.
By the inscribed angle theorem, the measure of angle PQR is half the measure of angle POR. Thus,
angle PQR = 1/2 * angle POR
= 1/2 * 90
= 45 degrees.
However, this is not the final answer since angle PQR is not a stand-alone angle, but rather a part of a right-angled triangle PQR.
Since the three angles in a triangle add up to 180 degrees, and we already know that angle PQR is 45 degrees, it follows that:
angle PRQ + angle PQR + angle QPR = 180 degrees
Since angle PQR = 45 degrees, we have:
angle PRQ + 45 + angle QPR = 180 degrees
Rearranging, we get:
angle PRQ + angle QPR = 135 degrees
Since angles PRQ and QPR are complementary angles (together they form a right angle), their sum is 90 degrees. Therefore,
angle PRQ + angle QPR = 90 degrees
Substituting this into the previous equation, we get:
90 degrees = 135 degrees
This is a contradiction, and hence our assumption that angle PQR measures 45 degrees is false.
Therefore, we conclude that angle PQR must measure 90 degrees, since it is the only angle that can satisfy the given conditions.
Learn more about inscribed angle theorem
brainly.com/question/5436956
#SPJ11
What is the equation of y=x^3 with the given transformations? Vertical compression by a factor of 1/7 ,horizontal shift 8 units to the left, reflection across the x axis
Answers
Answer:
y = (1/7)(x + 8)³
Step-by-step explanation:
We are given the function; y = x³
There is a vertical compression by a factor of 1/7 which means that we now have the function as;
y = (1/7)x³
We are told that it shifts by 8 units to the left. This means we will have;
f(x + 8)
This gives;
y = (1/7)(x + 8)³
The transformed equation of \(y=x^{3}\) is \(y=-\frac{1}{7} (x+8)^{3}\).
Given equation:- \(y=x^{3}\)
Applying the given transformations, we have:
To have a vertical compression by a factor of \(\frac{1}{7}\), we need to multiply the function by \(\frac{1}{7}\). So, we have:
\(y=\frac{1}{7} x^{3}\)
To have a horizontal shift by 8 units to the left, we need to add 8 to x. So, we have:
\(y=\frac{1}{7} (x+8)^{3}\)
Lastly, to have a reflection over the x-axis, we need to multiply the function by −1. So, we have:
\(y=-\frac{1}{7} (x+8)^{3}\)
Therefore, the transformed equation is \(y=-\frac{1}{7} (x+8)^{3}\)
For more information:
https://brainly.com/question/22821177
The 2017 balance sheet of Kerber's Tennis Shop, Inc., showed long-term debt of $5 million, and the 2018 balance sheet showed long-term debt of $5.2 million. The 2018 income statement showed an interest expense of $165,000. During 2018, the company had a cash flow to stockholders for the year was $70,000. Suppose you also know that the firm’s net capital spending for 2018 was $1,370,000, and that the firm reduced its net working capital investment by $69,000. What was the firm’s 2018 operating cash flow, or OCF?
Griffin's Goat Farm, Inc., has sales of $686,000, costs of $332,000, depreciation expense of $65,000, interest expense of $48,500, and a tax rate of 24 percent. What is the net income for this firm?
Answers
The net income for Griffin's Goat Farm, Inc., was \(\$184,340\).
The operating cash flow (OCF) for Kerber's Tennis Shop, we can use the following formula:
\(OCF = EBIT + Depreciation - Taxes + \triangle Working Capital\)
where EBIT is earnings before interest and taxes.
Calculate EBIT by subtracting interest expense from operating income:
EBIT = Operating Income - Interest Expense
We do not have the information for operating income, but we can use the fact that interest expense was. \(\$165,000\) to calculate EBIT.
EBIT = Interest Expense / (1 - Tax Rate)
= \(\$165,000 / (1 - 0)\)
= \(\$165,000\)
Calculate the change in working capital (Δ Working Capital). We are told that the company reduced its net working capital investment by \(\$69,000\), which means that working capital increased by \(\$69,000\).
Therefore:
\(\triangle Working Capital = \$69,000\)
Now, we can calculate OCF:
OCF = EBIT + Depreciation - Taxes + Δ Working Capital
=\(\$165,000 + 0 - 0 +\ $69,000\)
=\(\$234,000\)
Therefore, the firm’s 2018 operating cash flow (OCF) was \(\$234,000\) .
To calculate the net income for Griffin's Goat Farm, we can use the following formula:
Net Income = EBIT - Interest Expense - Taxes
where EBIT is earnings before interest and taxes. We can calculate EBIT as:
EBIT = Sales - Costs - Depreciation
= \(\$686,000 - \$332,000 - \$65,000\)
=\(\$289,000\)
Next, we need to calculate taxes. We are given a tax rate of 24%, so:
Taxes = Tax Rate x (EBIT - Depreciation)
= \(0.24 \times (\$289,000 - \$65,000)= \$56,160\)
Now, we can calculate net income:
Net Income = EBIT - Interest Expense - Taxes
= \(\$289,000 - \$48,500 - \$56,160= \$184,340\)
For similar questions on Income
https://brainly.com/question/30157678
#SPJ11
I don’t quite understand these two questions, anyone mind helping me out?

Answers
nd a function for the model for consumer expenditure (revenue for the vendor), where x is the price in dollars, data from 20 ≤ x ≤ 32. (round all numerical values to three decimal places.)
Answers
To model the consumer expenditure (revenue for the vendor) as a function of price, we can use a linear equation in the form of:
Expenditure = m * Price + b
Where:
Expenditure represents the consumer expenditure or revenue for the vendor.
Price is the price of the product in dollars.
m is the slope of the linear equation.
b is the y-intercept of the linear equation.
To determine the values of m and b, we need additional data points or information about the relationship between price and consumer expenditure. Without specific data points, it is not possible to determine the exact values of m and b.
However, if you have a specific data set or information on the relationship between price and consumer expenditure within the range of 20 to 32 dollars, I can assist you in calculating the values of m and b using linear regression or provide alternative modeling approaches based on the available information.
To know more about expenditure refer here:
https://brainly.com/question/31497984
#SPJ11
Put the following equation of a line into slope-intercept form, simplifying all fractions.
2y-4x=18
Answers
Answer:
y = 2 x + 9
Step-by-step explanation:
(* ̄3 ̄)╭
Answer:
Here is the answer
Step-by-step explanation:
y = 2x + 9please help me. (And if u want pls explain)
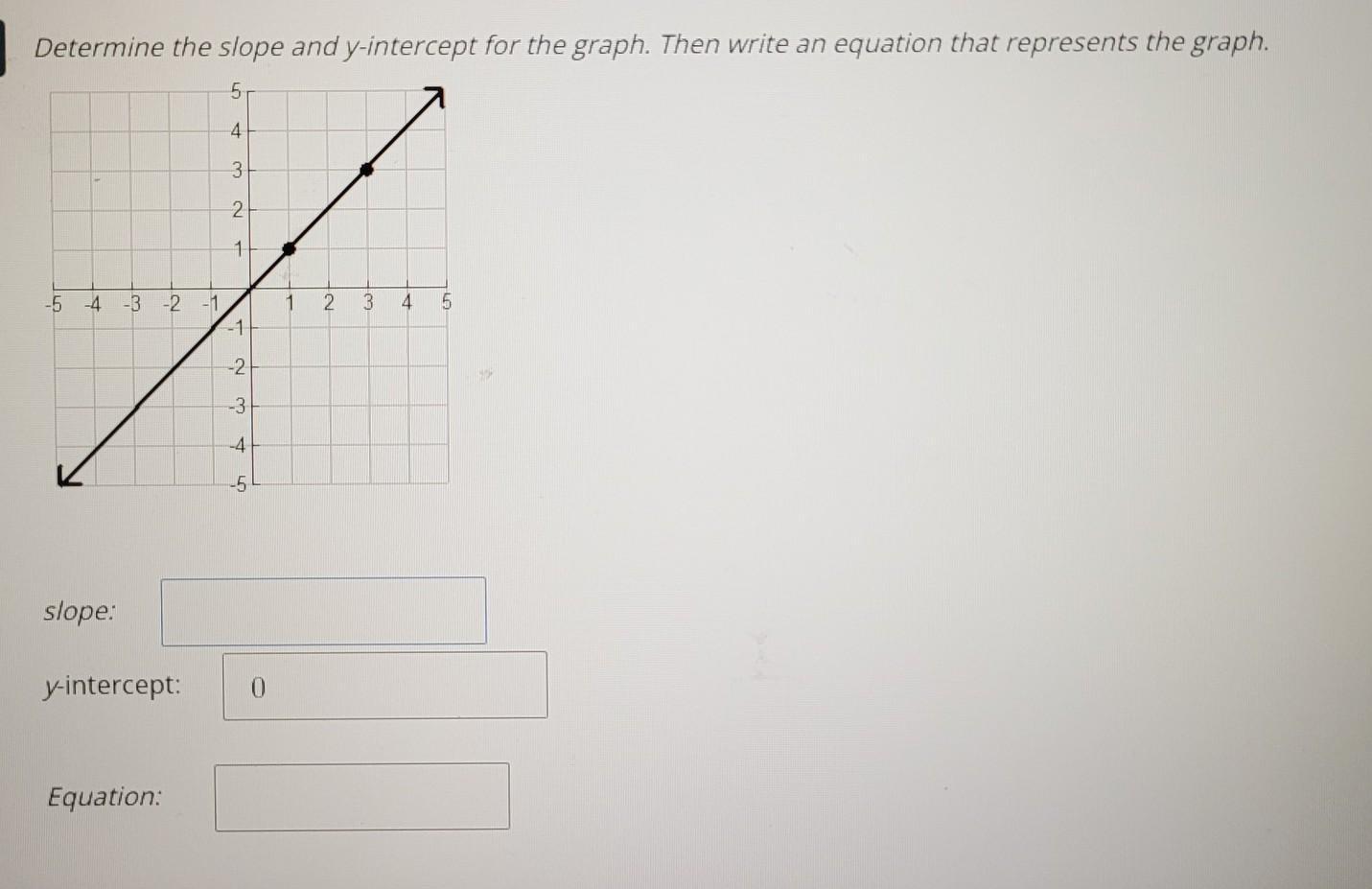
Answers
Y-intercept : 0
Use the equation y=mx+b
Put the slope in for m, and the y-intercept in for b
This would make the equation :
y=1x+0
I found the slope by finding two points on the graph, yours are marked. You go up 2, and right 2 to get from one point to the next so it would be a fraction. 2/2. You can simplify this to 1/1, which is the same thing as 1.
Determine the monthly payment of a $4,500 loan at 12% interest for 48 months.
Answers
The monthly payment on a loan of $4,500 at 12% interest for a period of 48 months is: $128.34.
How to Calculate the Monthly Payment on a Loan?The monthly payment for a $4,500 loan at 12% interest for 48 months can be calculated using the formula:
M = P * (r(1 + r)^n) / ((1 + r)^n - 1)
Where:
M = the monthly payment
P = the principal (the amount of the loan)
r = the monthly interest rate (12% divided by 12 months)
n = the number of payments (48 months)
So the calculation is:
M = 4,500 * (0.01(1 + 0.01)^48) / ((1 + 0.01)^48 - 1)
This comes out to be $128.34.
Learn more about monthly payment on a loan on:
https://brainly.com/question/28106777
#SPJ1
Find f'(2), where f(t)=u(t)• v(t), u(2)= (1, 2, -1), u'(2)=(3, 0, 4) and v(t)= (t,t^2,t^3).
Answers
The value of f'(2) by the given data is 35.
We are given that;
f(t)=u(t)• v(t)
u(2)= (1, 2, -1),
u'(2)=(3, 0, 4) and \(v(t)= (t,t^2,t^3)\)
Now,
A function in mathematics is a rule that assigns a unique output to each input. For example, if f(x) = x + 2, then f(3) = 5, f(-1) = 1, and so on. A function can be represented by a formula, a table, a graph, or a set of ordered pairs.
To find f’(2), we need to use the product rule for vector-valued functions:
\(f'(t) = u'(t) v(t) + u(t) v'(t)\)
Then, plugging in t = 2 and the given values of u(2), u’(2), v(2) and v’(t), we get:
\(f'(t) = u'(t) v(t) + u(t) v'(t)\)
= (3, 0, 4) • (2, 4, 8) + (1, 2, -1) • (1, 2t, 3t^2)
= (3)(2) + (0)(4) + (4)(8) + (1)(1) + (2)(4) + (-1)(12)
= 6 + 0 + 32 + 1 + 8 - 12 = 35
f’(2) = 35.
Therefore, by the function answer will be 35.
Learn more about function here:
https://brainly.com/question/2253924
#SPJ4
Frank bought 18 water bottles and 28 candy bars for a reunion. Water bottle cost 1.80 for a six pack. Candy bars cost 4.20 for 6-pack? How much money did he spend not including tax on water and candy
Answers
Answer:
$17.60
Step-by-step explanation:
Let’s start by first finding the cost of 1 candy bar. We have to divide 1.80 by 6 to find the cost of 1 water bottle and 4.20 divided by 6 to find the cost of 1 candy bar. 1 water bottle= 30 cents (0.3) and 1 candy bar= 70 cents (0.7). Now, to find how much he spent on 18 water bottles we must multiply 18 by 0.3 which = $60 and multiply 28 by 0.7 = $19.60 (19.6). Now add 19.60 + 60 = 79.60 (79.6)
So, Frank spent $79.60 on food total. Sorry if I got it wrong, but hope this helps!
What is the contrapositive for this conditional statement? Is the contrapositive true?
If a number is even then it is divisible by 2.
Answers
Answer:
It the statement is true, then the contrapositive is also logically true. If the converse is true, then the inverse is also logically true. If two angles are congruent, then they have the same measure.
converse, inverse, contrapositive.
statement. if p, then q
inverse. if not p, the not q
contrapositive. if not q, then not p
Sorry about the screen, I’m using my laptop! Please help me if you know the answer my dumb mind can’t work it out

Answers
Answer:
5.9 hours, 10£
Step-by-step explanation:
For the first question, you must find how long it would take 1 knitter to do all the work, and you can move on from there. Since it takes 11 knitters 7 hours, it would take 1 knitter 11 times as long, meaning it would take 7*11=77 hours for 1 knitter. Now we can divide 77 hours by 13 as 13 knitters could to it in 1/13 of the time. Dividing 77 by 13 we get 5.9 hours.
For the second question, if each person pays 9£, and there are 10 people, in total they are paying 10*9£=90£. This means that if the spit it up between 9 people instead, each would by 90£/9=10£. This means they would each have to pay 10£.
hree people are asked to throw a fair die. what is the probability that all of them get the same number
Answers
The probability that all of them get the same number is 1/36.
Given :
Three people are asked to throw a fair die.
Probability :
Probability is a branch of mathematics that deals with the occurrence of a random event.
In one dice probable outcomes 1, 2, 3, 4, 5 and 6
Total out comes in three dice = ( 6 * 6 * 6 = 216 )
Probability of getting 1 = 1/216
Similarly for 2, 3, 4, 5 and 6
Probability of getting same number = 6 * 1/6 * 1/6 * 1/6
= 6*1/6 * 1 * 1 / 6 * 6
= 6/6 * 1/36
= 1 * 1/36
= 1/36
Learn more about the probability here:
https://brainly.com/question/11234923
#SPJ4
Use the order of operations to find answers to these facts (GEMDAS)
step 1 THE HIGHEST TEMPERATURE (F°) EVER RECORDED IN THE UNITED STATES WAS IN DEATH VALLEY, CA IN 1913. WHAT WAS THE RECORD TEMPERATURE? (6+4)x^{2} +34
Answers
Answer:
134
Step-by-step explanation:
which expression is equivalent to 6p + 6p?
A 12p
B 36p
C 12 + 2p
D p ^6
Answers
Answer:
A
Step-by-step explanation:
They both share the same variable p, therefore you add the numbers to get the answer
Answer:
=12p
Step-by-step explanation:
fill in the missing number: 0,1,1,2,3,5,8,13,-,34,55
Answers
The missing number of the series is 21.
The given sequence appears to follow the pattern of the Fibonacci sequence, where each number is the sum of the two preceding numbers. The Fibonacci sequence starts with 0 and 1, and each subsequent number is obtained by adding the two previous numbers.
Using this pattern, we can determine the missing number in the sequence.
0, 1, 1, 2, 3, 5, 8, 13, -, 34, 55
Looking at the pattern, we can see that the missing number is obtained by adding 8 and 13, which gives us 21.
Therefore, the completed sequence is:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.
To learn more about number here:
https://brainly.com/question/32210789
#SPJ4
The missing number in the sequence 0, 1, 1, 2, 3, 5, 8, 13, -, 34, 55 is 21.
To find the missing number in the sequence 0, 1, 1, 2, 3, 5, 8, 13, -, 34, 55, we can observe that each number is the sum of the two preceding numbers. This pattern is known as the Fibonacci sequence.
The Fibonacci sequence starts with 0 and 1. To generate the next number, we add the two preceding numbers: 0 + 1 = 1. Continuing this pattern, we get:
011235813213455Therefore, the missing number in the sequence is 21.
Learn more:About fill in here:
https://brainly.com/question/182137
#SPJ11
Write each product or quotient in scientific notation. Round to the appropriate number of significant digits.
(4.237× 10⁴) (2.01 × 10⁻²)
Answers
The product of (4.237 × 10⁴) and (2.01 × 10⁻²) in scientific notation, rounded to the appropriate number of significant digits is 8.54 × 10².
To write the product of (4.237 × 10⁴) and (2.01 × 10⁻²) in scientific notation, we can multiply the coefficients and add the exponents.
(4.237 × 10⁴) (2.01 × 10⁻²) = (4.237 × 2.01) × (10⁴ × 10⁻²)
Multiplying the coefficients, we get:
(4.237 × 2.01) = 8.53737
For the exponent, we can add 4 and -2:
10⁴ × 10⁻² = 10⁻² (10⁴) = 10²
Combining the coefficient and the exponent, we have:
8.53737 × 10²
Rounding to the appropriate number of significant digits, we get:
8.54 × 10²
Therefore, the product of (4.237 × 10⁴) and (2.01 × 10⁻²) in scientific notation ≈ 8.54 × 10².
To know more about scientific notation refer here:
https://brainly.com/question/16936662#
#SPJ11
calculate the volume that lies within the cylinder, x2 y2 = 9 and between the xy-plane and the paraboloid z = x2 y2.
Answers
Answer:
\(\frac{81\pi}{2}\)
Step-by-step explanation:
The explanation and triple integration steps are shown in the attached document.

Two containers, A and B begin with equal volumes of liquid.
120ml is then poured from A to B.
Container B now contains 4 times as much liquid as A.
Find the volume of liquid left in container A at the end
Answers
Answer:
Suppose A and B , both has initial volume, say x
120 ML is poured from B to A, then new volumes of A and B will be:
new volume of A (x-120)
new volume of B (x+120)
Volume of B is now four times volume of A, then
(x+120)= 4(x-120)
(x+120)=4x-180
3x=600
x=200
So, the initial volume of A and B containers is 200
So, at the end, volume of container A = 200-120=80
Hence the answer is 80 :
Step-by-step explanation:
The equation of a line given two points needs to be found. Samuel claims that slope-intercept form will generate the equation and Helena claims that point-slope form will find the equation. Who is correct?
Answers
Answer:
Helena is correct.
Step-by-step explanation:
The slope intersept form of the line is
y = m x + c
where, m is the slope and c is the intersept.
The point slope form of the equation is
\(y - y'= \frac{y''-y'}{x''-x'}\times (x-x')\)
So, if there are two points are given, the equation of line is found by the point slope form.
So, Helena is correct.
Write tan 41π/36 in terms of the tangent of a positive acute angle.
Answers
tan(41π/36) can be written in terms of the tangent of a positive acute angle as (tan((1/9)π) + tan((37/36)π)) / (1 - tan((1/9)π)tan((37/36)π))
To express tan(41π/36) in terms of the tangent of a positive acute angle, we need to find an angle within the range of 0 to π/2 that has the same tangent value.
First, let's simplify 41π/36 to its equivalent angle within one full revolution (2π):
41π/36 = 40π/36 + π/36 = (10/9)π + (1/36)π
Now, we can rewrite the angle as:
tan(41π/36) = tan((10/9)π + (1/36)π)
Next, we'll use the tangent addition formula, which states that:
tan(A + B) = (tan(A) + tan(B)) / (1 - tan(A)tan(B))
In this case, A = (10/9)π and B = (1/36)π.
tan(41π/36) = tan((10/9)π + (1/36)π) = (tan((10/9)π) + tan((1/36)π)) / (1 - tan((10/9)π)tan((1/36)π))
Now, we need to find the tangent values of (10/9)π and (1/36)π. Since tangent has a periodicity of π, we can subtract or add multiples of π to get equivalent angles within the range of 0 to π/2.
For (10/9)π, we can subtract π to get an equivalent angle within the range:
(10/9)π - π = (1/9)π
Similarly, for (1/36)π, we can add π to get an equivalent angle:
(1/36)π + π = (37/36)π
Now, we can rewrite the expression as:
tan(41π/36) = (tan((1/9)π) + tan((37/36)π)) / (1 - tan((1/9)π)tan((37/36)π))
Since we are looking for an angle within the range of 0 to π/2, we can further simplify the expression as:
tan(41π/36) = (tan((1/9)π) + tan((37/36)π)) / (1 - tan((1/9)π)tan((37/36)π))
Therefore, tan(41π/36) can be written in terms of the tangent of a positive acute angle as the expression given above.
For more about tangent:
https://brainly.com/question/19064965
#SPJ4
need help with this! show work please!

Answers
Answer:
(a) 1/2
(b) $1,080,000
(c) 72°
Step-by-step explanation:
We have to find the ratio in which the money is being distributed
To do this first add up the individual values in the ratio 5:3:2 which represents the ratio C:D:E for apportioning savings
5 + 3 + 2 = 10
Chris's share = 5/10 = 1/2
Danny's share = 3/10
Evelyn's share = 2/10 = 1/5
Answers
(a) Fraction of Danny's share = 1/2
(b) If Danny is to receive $540,000 and his share is 1/2 of total savings then the total savings = 2 x 540,000 = $1,080,000
(c) The ratio of the angles in a pie chart will be the same as the ratio of the division. A pie chart shows the relative shares as part of a circle. Since a circle contains 360° , the angle of the sector that represents Evelyn's share will be 1/5 x 360 = 72°
Choose the function that correctly identifies the transformation of f(x) = x2 shifted three units to the left and five units up.
og*) = (x - 3)2-5
og(x) = (x - 3)2 + 5
og(x) = (x + 3)2 + 5
o g() = (x + 3)2-5
Answers
The functions that correctly identify the transformation of f(x) = x² shifted three units to the left and five units up is
g(x) = (x + 3)² + 5
Option C is the correct answer.
What is a function?A function has an input and an output.
A function can be one-to-one or onto one.
It simply indicated the relationships between the input and the output.
Example:
f(x) = 2x + 1
f(1) = 2 + 1 = 3
f(2) = 2 x 2 + 1 = 4 + 1 = 5
The outputs of the functions are 3 and 5
The inputs of the function are 1 and 2.
We have,
The function that correctly identifies the transformation of f(x) = x² shifted three units to the left and five units up is:
g(x) = (x + 3)² + 5
To see why, we can use the following steps:
To shift a function three units to the left, we replace "x" with "(x + 3)".
This is because for any value of "x", "x + 3" represents a point that is three units to the left of "x".
To shift a function five units up, we add 5 to the entire function.
This is because for any value of "x", the value of the function is increased by 5 units.
Combining these transformations, we get:
g(x) = (x + 3)² + 5
This function represents a parabola that is shifted three units to the left and five units up from the original function f(x) = x^2.
Thus,
The functions that correctly identify the transformation of f(x) = x² shifted three units to the left and five units up is
g(x) = (x + 3)² + 5
Learn more about functions here:
https://brainly.com/question/28533782
#SPJ7
Mike, a Salvation Army bell ringer, has 20% as many quarters as nickels in his cup. If Mike has $6.00 in quarters and nickels, how many nickels does he have?
Answers
If If Mike has $6.00 in quarters and nickels, then the number of nickels Make have are 60.
Let's assume that the number of nickels in Mike's cup is "N." Since Mike has 20% as many quarters as nickels, the number of quarters can be expressed as 0.20N.
Now, we know that the total value of the quarters and nickels is $6.00. The value of each nickel is $0.05, and the value of each quarter is $0.25.
So, we can set up the equation:
0.05N + 0.25(0.20N) = 6.00
Now, let's solve for N:
0.05N + 0.05N = 6.00
0.10N = 6.00
N = 6.00 / 0.10
N = 60
So, Mike has 60 nickels in his cup.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ4