A Health Authority has undertaken a simple random sample of 1 in 5 of the medical practices in its region. The 150 practices in the sample have a mean of 8,400 patients registered with
the practices, with a standard deviation of 2,000 patients. (a) Obtain a point estimate and an approximate 95% confidence interval for the mean number of patients registered with a practice within the region and hence find a 95% confidence interval
for the total number of patients registered with practices within the region.
(b) Additional information is available from the sample: the 150 practices within the sample have a mean of 3.2 doctors, with a standard deviation of 1.2 doctors. The correlation between the number of patients and the number of doctors within a practice is 0.8. Obtain a point
estimate and an approximate 95% confidence interval for the ratio of patients per doctor.
Answers
The approximate 95% confidence interval for the mean number of patients registered with a practice within the region is (8015.94, 8784.06).
Point EstimateA point estimate of the population parameter refers to the point or a single value which is used to estimate the population parameter. In the given case, the population parameter is the mean number of patients registered with a practice within the region.
Therefore, the point estimate for the mean number of patients registered with a practice within the region would be the sample mean:
8,400 patients registered with the practices
95% Confidence Interval
The formula to obtain the approximate 95% confidence interval for the population mean of number of patients registered with a practice within the region is given by:
\($$\left(\bar{x}-t_{n-1,\alpha/2} \frac{s}{\sqrt{n}}, \bar{x}+t_{n-1,\alpha/2} \frac{s}{\sqrt{n}}\right)$$\)
where: n = sample size;
s = sample standard deviation;
\($\bar{x}$\) = sample mean;
\($\alpha$\) = level of significance;
\($t_{n-1,\alpha/2}$\) = critical value of t-distribution at α/2 and (n-1) degrees of freedom.
Substituting the given values, we have:
\($$\left(8400 - 1.96\cdot \frac{2000}{\sqrt{150}}, 8400 + 1.96\cdot \frac{2000}{\sqrt{150}}\right)$$\)
The interval is given by (8015.94, 8784.06).
Hence, the approximate 95% confidence interval for the mean number of patients registered with a practice within the region is (8015.94, 8784.06).
Learn more about mean :
https://brainly.com/question/31098693
#SPJ11
Related Questions
Each side of a square is 3inches long.a student increases the length of each side by 3inches.the are of the new Square is how many times the area of original square?
A=2
B-3
C=4
D=a
Answers
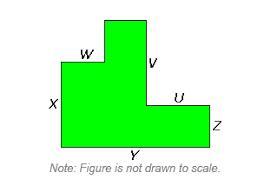
If U = 6 feet, V = 7 feet, W = 4 feet, X = 7 feet, Y = 12 feet, and Z = 4 feet, what is the area of the object?
A. 84 square feet
B. 66 square feet
C. 132 square feet
D. 74 square feet
Answers
The total area of the composite figure is 74 square feet
Calculating the area of the figureFrom the question, we have the following parameters that can be used in our computation:
The composite figure (see attachment)
Also, we have
U = 6 feet, V = 7 feet, W = 4 feet, X = 7 feet, Y = 12 feet, and Z = 4 feet
The total area of the composite figure is the sum of the individual shapes
So, we have
Area = XW + (Y - W - U) * (V + Z) + ZU
This gives
Area = 7 * 4 + (12 - 4 - 6) * (7 + 4) + 4 * 6
Evaluate
Area = 74
Hence. the total area of the figure is 74 square feet
Read more about area at
brainly.com/question/26403859
#SPJ1
Solve the following system of equations using substitution
-3x+6y=12
2y=x+4
Answers
From the equation, 0 = 0. Therefore, the system of equation has infinite number of solutions.
How to solve system of equation?System of equation can be solved using different method such as elimination method, graphical method and substitution method.
Let's use substitution method to solve the system of equation as follows;
-3x + 6y = 12
2y = x + 4
x = 2y - 4
Hence, let's substitute the value of x in equation(i)
-3(2y - 4)+ 6y = 12
-6y + 12 + 6y = 12
-6y + 6y = 12 - 12
0 = 0
Therefore, the system of equations has infinite solutions.
learn more on system of equation here: https://brainly.com/question/15313209
#SPJ1
ASAP i have three other math questions posted as well i give 100 for each and brainlit to the right answers
Triangle NMO is drawn with vertices N(−5, 2), M(−2, 1), O(−3 , 3). Determine the image vertices of N′M′O′ if the preimage is reflected over x = −2.
N′(5, −2), M′(2, 1), O′(3, 3)
N′(−2, 2), M′(1, 1), O′(0, 3)
N′(1, 2), M′(−2, 1), O′(−1, 3)
N′(−5, −2), M′(−2, −1), O′(−3, −3)
Answers
Answer: Option (C): N′(1, 2), M′(−2, 1), O′(−1, 3).
Step-by-step explanation:
To reflect the preimage over x = -2, we can use the formula for reflecting a point (x, y) over a vertical line x = a:
(x', y) = (2a - x, y)
In this case, the vertical line is x = -2, so a = -2.
So we can find the image vertices as follows:
N' = (2(-2) - (-5), 2) = (4 + 5, 2) = (9, 2)
M' = (2(-2) - (-2), 1) = ( -4 + 2, 1) = (-2, 1)
O' = (2(-2) - (-3), 3) = (-4 + 3, 3) = (-1, 3)
Therefore, the image vertices of N'M'O' after reflecting the preimage over x = -2 are N'(9, 2), M'(-2, 1), O'(-1, 3). So the answer is option (c): N′(1, 2), M′(−2, 1), O′(−1, 3).
On a Sunday night, there are four people on a bus. The bus has five stops left before it end sits route. Suppose each person will get off the bus at one of the stops, and will do so randomly
1- How many different ways could the people get off the bus?
2- What is the probability that all four people get off the bus on the first stop?
3- What is the probability that all four people get off the bus on the same stop?
4- What is the probability that exactly three of the four people get off the bus on the same stop?
Answers
There are two possible outcomes of this experiment either success p or failure q. It has a given number of trials and all trials are independent therefore it is binomial probability distribution.
1- 5 ways
2- 5/16
3- 1/16
4- 1/16
In the question given above n= 5 p =1/2 q= 1/2 r is the given point.
Part 1:The number of ways in which different people get off the bus can be calculated using combinations since the order is not essential. Therefore
nCr= 5C4= 5 ways
2. Part 2:
The probability that all four people get off the bus on the first stop is given by :
P (x= 1)= 5C1 (1/2)^0(1/2)^4= 5(1/2)^4= 5/16
3. Part 3:- The probability that all four people get off the bus on the same stop.
P (x= x)= 5C5 (1/2)^0(1/2)^4= 1(1/2)^4= 1/16
4. Part 4- The probability that exactly three of the four people get off the bus on the same stop.
P (x= x)= 5C5 (1/2)^3(1/2)^1= 1(1/2)^4= 1/16
For binomial distribution click
https://brainly.com/question/15246027
https://brainly.com/question/13542338
The perimeter of a rectangle is 70 cm. If its length is decreased by 5 cm and its width is increased by 5 cm, its area will increase by 50 cm². Find the length and the width of the original rectangle.
Answers
The requried dimension of the original rectangle is given as length = 25 cm, width = 10 cm.
What is a rectangle?The rectangle is 4 sided geometric shape whose opposites are equal in length and all angles are about 90°.
Let the length and width of the original rectangle be x and y,
According to the quesiton,
The perimeter of a rectangle is 70 cm.
2 [x + y] = 70
x + y = 35 - - - -(1)
Now,
its length is decreased by 5 cm and its width is increased by 5 cm, its area will increase by 50 cm².
Area of the new rectangle = area of the original rectangle + 50
(x - 5)(y + 5) = xy + 50
from equation 1,
(x - 5)(35 - x + 5) = x(35 - x) + 50
-x² - 200 + 40x + 5x = 35x - x² + 50
45x - 35x = 50 + 200
10x = 250
x = 25
Now,
y = 35 - 25
y = 10
Thus, the requried dimension of the original rectangle is given as length = 25 cm, width = 10 cm.
Learn more about rectangles here:
brainly.com/question/15019502
#SPJ1
Determine algebraically whether the function is even odd.
Answers
"To determine if a function is even or odd, check if it satisfies the properties of evenness or oddness algebraically."
When determining whether a function is even or odd, we need to apply specific algebraic conditions to verify its symmetry properties. An even function satisfies the condition f(-x) = f(x) for all x in its domain, meaning that substituting -x into the function yields the same result as using x. On the other hand, an odd function satisfies the condition f(-x) = -f(x) for all x in its domain, indicating that substituting -x into the function results in the negative of the value obtained using x. By applying these algebraic tests, we can determine if a function exhibits evenness, oddness, or neither, which provides insight into its symmetry properties.
"To determine if a function is even or odd, check if it satisfies the properties of evenness or oddness algebraically."
learn more about even and odd functions here:
https://brainly.com/question/27880904
#SPJ11
What is 13 - 4 x = 1 - x?
Answers
Answer:
x=4
Step-by-step explanation
Answer:
x = 4
Explanation:
PLEASE HELP ME I CAN’T WAIT AROUND TOO LONG
Answers
Answer:
The components of the vector in unit vector notation are found by breaking the vector into its x and y components, where x is the horizontal component and y is the vertical component. To do this, we can use trigonometry:
x = magnitude * cos(angle) = 32.1 * cos(73.0°)
y = magnitude * sin(angle) = 32.1 * sin(73.0°)
Once we have the x and y components, we can divide each component by the magnitude of the vector to get the unit vector notation:
B = (x / magnitude, y / magnitude) = (x / 32.1, y / 32.1)
Note that the magnitude of the vector is 32.1 and the angle is 73.0°. You'll need to use a calculator or mathematical software to find the cosine and sine of the angle, and then divide the x and y components by the magnitude to find the unit vector notation.
Step-by-step explanation:
53 points!!! find x. do not round your answer. 5cm 6cm 12cm x

Answers
Answer:
16.6
Step-by-step explanation:
By the property of intersecting secants.5(5+x) = 6(6+12)-> 25 + 5x = 6*18-> 5x = 108 - 25-> 5x = 83-> x = 83/5-> x = 16.6Perimeter is 25 cm, find x 10 8.2 cm
Answers
slope form of the line, where y represents the height, in feet, of the bucket relative to the top of the well after x seconds?
Answers
To determine the specific equation for the situation described, we would need more information about the relationship between time and the height of the bucket.
The slope form of the line representing the height, y, of the bucket relative to the top of the well after x seconds can be written as:
y = mx + b
Here, m represents the slope of the line, and b represents the y-intercept.
To determine the specific equation for the situation described, we would need more information about the relationship between time and the height of the bucket.
Learn more about equation from
https://brainly.com/question/29174899
#SPJ11
Factorize this 5y2 + 2y – 3a2?
Answers
Answer:
y(5y +2) -3a²
Step-by-step explanation:
that is the solution above
f(x) is obtained from x by replacing the first bit with 00. for example, f(101) = 0001. select the correct description of the function f.
Answers
In general, for any binary number x, the function f(x) replaces the first bit with "00".
The correct description of the function f(x) is that it performs a bitwise operation on x where it replaces the first bit with "00".
In binary representation, each digit in a number is called a bit. For example, the number 101 can be represented in binary as "1 0 1", where each digit is a bit.
When we apply the function f(x) to the number 101, it replaces the first bit (which is "1") with "00". So, the resulting number is 0001.
To know more about number visit:
brainly.com/question/3589540
#SPJ11
Which of the following statements says that a number is between -5 and 5?
|x| < 5
|x| > 5
|x| = 5
Answers
Answer:
|x| > 5 if correct pls follow
Please help.
Is algebra.

Answers
Answer:
The same as the person above me
Step-by-step explanation:
1.
- 2,3
2.
-X=2
Y=3
Answer these also with standard pls

Answers
a. Slope 2 and y-intercept 3
Slope-intercept form: \(\bold{y=2x+3}\)
Standard form: \(\bold{2x-y=-3}\)
b. Slope \(\frac{3}{5}\) and y-intercept -6
Slope-intercept form: \(\bold{y=\frac{3}{5}x-6}\)
Standard form: \(\bold{3x-5y=30}\)
c. Slope \(-\frac{3}{2}\) and y-intercept 9
Slope-intercept form: \(\bold{y=-\frac{3}{2}x+9}\)
Standard form: \(\bold{3x+2y=18}\)
d. Slope -3 and y-intercept 0
Slope-intercept form: \(\bold{y=-3x}\)
Standard form: \(\bold{3x+y=0}\)
A large school district held a district-wide track meet for all high school students. For the 2-mile run, the population of female students participating follows a Normal distribution and had a mean running time of 8.8 minutes with standard deviation of 3.3 minutes. The population of male students participating also follows a Normal distribution and had a mean running time of 7.3 minutes with standard deviation 2.9 minutes. Suppose 8 female students and 8 male students who participated in the 2-mile run are selected at random from each population. Let xF represent the sample mean running time for the female students, and let xM represent the sample mean running time for the male students. a. Find and interpret the mean and standard deviation of the sampling distribution of the difference in sample means xF − xM. b. Find the probability of getting a difference in sample means xF − xM that is less than 0.
Answers
Answer:
If the question has
What are the mean and standard deviation of the sampling distribution of the difference in sample means x¯F−x¯M ?
It is E
Step-by-step explanation:
AP classroom uses the example with different end questions.
The mean and standard deviation of the sampling distribution of the difference in sample means xF − xM is 1.5 minutes(mean) and 1.533 minutes(std. dev) approx The probability of getting a difference in sample means xF − xM that is less than 0 is 0.0239 approx.
What is the distribution of random variable which is sum of normal distributions?Suppose that a random variable X is formed by n mutually independent and normally distributed random variables such that:
\(X_i = N(\mu_i , \sigma^2_i) ; \: i = 1,2, \cdots, n\)
And if
\(X = X_1 + X_2 + \cdots + X_n\)
Then, its distribution is given as:
\(X \sim N(\mu_1 + \mu_2 + \cdots + \mu_n, \: \: \sigma^2_1 + \sigma^2_2 + \cdots + \sigma^2_n)\)
For this case, it is given that:
Distribution of time taken for distance ran by female is Normal distribution and had a mean running time of \(\mu_F\) = 8.8 minutes with standard deviation of \(\sigma_F\) = 3.3 minutes.Distribution of time taken for distance ran by male is Normal distribution and had a mean running time of \(\mu_M\) = 7.3 minutes with standard deviation of \(\sigma_M\) = 2.9 minutes.Samples of size n = 8 are taken from both population.Estimated sample mean = population mean
Estimated sample standard deviation = population std. dev / √n
where n = sample size
Thus, we get:
\(\overline{x}_F = \mu_F = 8.8 \: \rm minutes\)\(s_F = \sigma_F/\sqrt{8} = 3.3/\sqrt{8} \approx 1.167 \: \rm minutes\)\(\overline{x}_M = \mu_M = 7.3 \: \rm minutes\)\(s_M = \sigma_M/\sqrt{8} = 2.9/\sqrt{8} \approx 1.053\: \rm minutes\)For sample of females, the distribution is \(X_F \sim N(\overline{x}_F = 8.8, s_F = 3.3/\sqrt{8})\)
For sample of males, the distribution is \(X_M \sim N(\overline{x}_M =7.3, s_M = 2.9/\sqrt{8})\)
Also, if we take distribution of difference between sample means(\(X_F - X_M = X_F + (-X_M)\), then it would be normal with mean = 8.8-7.3 = 1.5 minutes (as mean for \(-X_F\) will be -7.3 but same standard deviation) as factor gets squared for affecting standard deviation and variance)
and standard deviation is: \(s = \sqrt{s_F^2 + s_M^2} = \sqrt{3.3^2/8 + 2.9^2/8} \approx 1.553 \: \rm minutes\)
The distribution of difference between sample means is \(X_F - X_M \sim N(\overline{x} = 1.5, s = 1.533)\) approximately
We need \(P(X_F - X_M < 0)\)
Converting this distribution to standard normal distribution, we get:
\(P(X_F - X_M < 0) = P(Z < \dfrac{0 - \overline{x}}{s} \approx -1.98)\)
From the z-tables, we get the p value for Z = -1.98 as 0.0239
Thus, we get:
\(P(X_F - X_M < 0) = P(Z < \dfrac{0 - \overline{x}}{s} \approx -1.98) \approx 0.0239\)
Thus, the mean and standard deviation of the sampling distribution of the difference in sample means xF − xM is 1.5 minutes(mean) and 1.533 minutes(std. dev) approx The probability of getting a difference in sample means xF − xM that is less than 0 is 0.0239 approx.
Learn more about standard normal distribution here:
https://brainly.com/question/10984889
all you need is in the photo
please answer step by step

Answers
Converting Real Life Scale.. -Page 2-
NEED HELP ASAPPP 50 POINTS
(picture is linked belowww)
tysm like fr <33

Answers
The table with the scale measurements is given by the image shown at the end of the answer.
How to obtain the measurements?The measurements are obtained applying the proportion given for each table.
The symbols are given as follows:
': feet.'': inches.For the first table, we have that every inch on the table represents one feet in real life, hence:
2'' on the paper represents 2' in real life.2' on the paper represents 24' in real life. (as one feet = 12 inches, hence 24 inches = 24 feet according to the scale).0.5'' on the paper represents 0.5' in real life.9'' on the paper represents 9' in real life.For the second table, we have that every inch on the paper represents two feet in real life, hence the measurements are given as follows:
2'' on the paper represents 4' in real life.2' on the paper represents 48' in real life.0.5'' on the paper represents 1' in real life.9'' on the paper represents 18' in real life.More can be learned about scale measurements at https://brainly.com/question/29229124
#SPJ1

A package in the shape of a cuboid is placed on a table.
The package applies a force of 151.9 newtons on the table.
The package applies a pressure of 155 newtons/m² on the table.
The face in contact with the table is a rectangle of length 1.4 metres
and width x metres.
Work out the value of x.
Answers
The width of the face of the cuboid in contact with the table is approximately 0.78 meters.
What is cuboid?A cuboid is a solid in three dimensions with six rectangular faces, eight vertices, and twelve edges. Three dimensions, including length, breadth, and height, define a cuboid. A cuboid with integer edges is referred described as being perfect.
A package in the shape of a cuboid is placed on a table.
The package applies a force of 151.9 newtons on the table.
The package applies a pressure of 155 newtons/m² on the table.
We can use the formula for pressure, which is:
pressure = force / area
The face of the cuboid in contact with the table is a rectangle with length 1.4 meters and width x meters, so its area is:
area = length x width = 1.4x square meters
We know the pressure applied by the package on the table is 155 newtons/m², and the force applied is 151.9 newtons. So we have:
155 = 151.9 / (1.4x)
Solving for x, we get:
x = 151.9 / (1.4 x 155) ≈ 0.78 meters
Therefore, x = 0.78 meters.
To learn more about the cuboid;
https://brainly.com/question/29568631
#SPJ2
What is the directrix of the parabola with the following equation?
(y - 1)2 = -4(x - 1)
Answers
Answer:
x = 2
Step-by-step explanation:
you are selling tickets to a school play. students tickets cost 5.00 dollars and adults tickets cost 7.00. you sell a total of 125 tickets and collect 775.00 dollars. how many of each type of ticket did you sell? PLZ HELP SHOW WORK
Answers
Answer:adult tickets - 75 and student tickets - 50
Step-by-step explanation:
75x7=525 and 50x5=250, therefore 525+250=775
hope this helps
Question Content Area
Net Present Value
A project has estimated annual net cash flows of $15,000 for ten
years and is estimated to cost $47,500. Assume a minimum acceptable
rate of return of 20%. Use
Answers
The required rate of return (or minimum acceptable rate of return) is 20 percent. If the net cash flows are $15,000 per year for ten years, the total cash flow is $150,000. The project's cost is $47,500. We can now apply the net present value formula to determine whether or not the project is feasible.
Net Present Value (NPV) = Cash flow / (1 + r)^n - Cost Where, r is the discount rate, n is the number of years, and Cost is the initial outlay.
Net Present Value = 150000 / (1 + 0.20)^10 - 47500
Net Present Value = $67,482.22
Since the NPV is positive, the project is feasible. When calculating net present value, it's important to remember that a positive NPV implies that the project is expected to generate a return that exceeds the cost of capital, whereas a negative NPV indicates that the project is expected to generate a return that is less than the cost of capital, and as a result, it should be avoided.
Know more about NPV here:
https://brainly.com/question/32720837
#SPJ11
What is the volume of the rectangular prism?

Answers
In other word 63 yd^3
harley was tested 10 times and 9 of those times he choose the correct cup. what are the observational units?
Answers
In the experiment, the subject whose behavior is being assessed are observational units. The observational unit in this instance is Harley (Dog).
We will first investigate if canines can comprehend both non-human and human gestures in this investigation. The dogs were placed around 2.5 meters apart from the experimenter so that the researchers could test this. Two glasses were placed one on either side of the experimenter.
A gesture would be made at one of the cups by either the experimenter (pointing, bowing, or staring) or by a non-human object (a mechanical arm pointing, a doll pointing, or a stuffed animal looking). After then, the scientists would observe whether the dog would approach the cup that was pointed out. Six dogs were put to the test. We'll focus on one of the dogs who participated in both of his trial sets.
The four-year-old mixed breed dog was given the name Harley. Each of the ten trials in a set consisted of one gesture and one pair of cups. In order to see if Harley would approach a particular cup, the experimenter bowed toward it during one round of experiments.
To learn more about observational units link is here
brainly.com/question/29518080
#SPJ4
Solve the following set of linear differential equations using the eigenvalue method. Y₁' 2y1 + y2 + Y3 3/2 +43 Y3' = Y/1 = Y1 + y2 5
Answers
Using the eigenvalue method, general solution is given by,Y(t) = c₁ e⁰t [-1 1 1]ᵀ + c₂ e¹t [-3 3 -2]ᵀ + c₃ e⁵t [-1 -1 2]ᵀ
The set of linear differential equations are,
Y₁' = 2y1 + y2 + Y3
Y₂' = Y₁ + y2 + 4/3 Y3
Y₃' = 3/2 Y₁ + 4y2 + 3Y3
Eigenvalues and eigenvectors for the matrix A = [2 1 1;1 1 4/3;3/2 4 3] are obtained as follows:
For λ₁, Eigenvalue equation is:
|A - λI| = 0⟹ (2 - λ)(1 - λ)(3 - 3λ/2) - (1 - λ)(3 - λ/2) - (1 - λ)(4 - 4λ/3) = 0⟹ λ³ - 6λ² + 11λ - 6 = 0
This can be solved as follows:
Using synthetic division,6 | 1 -6 11 -6 ⟹ 1 0 11 0⟹ λ₁ = 0, λ₂ = 1, λ₃ = 5
For λ₁ = 0, (A - λ₁I)
X = 0 where X is the eigenvector associated with λ₁.
The equation is,A - λI = [2 1 1;1 1 4/3;3/2 4 3] - [0 0 0;0 0 0;0 0 0] = [2 1 1;1 1 4/3;3/2 4 3]
Rank(A - λI) = 2
For λ₂ = 1, (A - λ₂I)
X = 0 where X is the eigenvector associated with λ₂.
The equation is,
A - λI = [2 1 1;1 1 4/3;3/2 4 3] - [1 0 0;0 1 0;0 0 1] = [1 1 1;1 0 4/3;3/2 4 2]
Rank(A - λI) = 3
For λ₃ = 5, (A - λ₃I)
X = 0
where X is the eigenvector associated with λ₃.The equation is,
A - λI = [2 1 1;1 1 4/3;3/2 4 3] - [5 0 0;0 5 0;0 0 5] = [-3 1 1;1 -4/3 4/3;3/2 4 -2]
Rank(A - λI) = 2
For λ₁ = 0,
Eigenvector equation is,(A - λ₁I)X = 0⟹ [2 1 1;1 1 4/3;3/2 4 3] X = 0
Solving the above equation, we get the solution set as,X = C₁[-1 1 1]ᵀ
For λ₂ = 1,
Eigenvector equation is,(A - λ₂I)X = 0⟹ [1 1 1;1 0 4/3;3/2 4 2] X = 0
Solving the above equation, we get the solution set as,X = C₂[-3 3 -2]ᵀ
For λ₃ = 5,
Eigenvector equation is,(A - λ₃I)X = 0⟹ [-3 1 1;1 -4/3 4/3;3/2 4 -2] X = 0
Solving the above equation, we get the solution set as,X = C₃[-1 -1 2]ᵀ
General solution is given by,Y(t) = c₁ e⁰t [-1 1 1]ᵀ + c₂ e¹t [-3 3 -2]ᵀ + c₃ e⁵t [-1 -1 2]ᵀ
Learn more about eigenvalues at
https://brainly.com/question/33182127
#SPJ11
Yo, I need the answer to this, please please please

Answers
I need help figuring out how to find these measurements.

Answers
We will have the following:
First, from properties of the parallelograms we will have that MR = RP; thus:
\(\begin{gathered} 2(5(a+8))=12a+52\Rightarrow10a+80=12a+52 \\ \\ \Rightarrow2a=28\Rightarrow a=14 \end{gathered}\)Now, we will have that:
\(\begin{gathered} MR=110 \\ \\ RP=110 \\ \\ MP=220 \end{gathered}\)How to solve 3x - 1/2 = 8 1/2 please no links and do it step by step
Answers
Answer:
\(x=\frac{3}{2}\)
Step-by-step explanation:
Step 1. Put each term in \(3x-\frac{1}{2}\) over the common denominator 2.
\(\frac{6x}{2}-\frac{1}{2}\)
Therefore we have \((\frac{6x}{2}-\frac{1}{2})=4\)
Step 2.
Combine \(\frac{6x}{2}-\frac{1}{2}\) into a single fraction.
\(\frac{6x-1}{2}\)
Therefore we have \((\frac{1}{2}(6x-1))=4\) or \(\frac{6x-1}{2}=4\)
Step 3.
Multiply both sides by a constant to simplify the equation.
Multiply both sides of \(\frac{6x-1}{2}=4\) by 2:
\(\frac{2*(6x-1)}{2}=4*2\)
Step 4.
Cancel the common terms in the numerator and denominator of \(\frac{2*(6x-1)}{2}\)
Then we get \(\frac{2}{2}*(6x-1)\) which simplifies to \((6x-1)\)
So all together we have \((6x-1)=2*4\)
Step 5.
Multiply 2 and 4 together and remove the parenthesis.
\(6x-1=8\)
Step 6.
Isolate terms with the variable x to the left hand side.
So add 1 to both sides:
\(6x+(1-1)=8+1\)
Evaluate \(1-1=0\) which cancels out
Step 7.
Add the like terms on the right side:
\(6x=9\)
Step 8.
Divide both sides by a constant to simplify the equation.
Divide both sides of \(6x=9\) by 6.
\(\frac{6x}{6} =\frac{9}{6}\)
Any non-zero number divided by itself is 1.
\(x=\frac{9}{6}\) which simplifies to \(x=\frac{3}{2}\)