A hotel charges $139 per night for a room. What is the cost for 6 nights?
HELP GIVEN BRAINLY POINTS
Answers
Answer: The correct answer is 834.
Step-by-step explanation: The way to do this problem is multiply the amount of money it costs for 1 night, times how many nights someone stayed. You do that by multiplying 139 x 6 = 834.
$834, the cost of 6 nights is $834
we know that 1 night =$139
therefore 6 nights =$139 ×6=$834
it is a simple linear equation word problem
if it is 7 nights then the answer would be
7×$139=$973
8 nights
8×$139=$1112
Learn more about linear equations on
brainly.com/question/14323743
Related Questions
If the random variable X is distributed normally with a mean of 0 and a standard deviation of 1, which of the following probabilities is not correct?
a. P(x ≥ 1) =.1587
b. P(x < 2) =.9772
c. P(x = 0) =.50
d. P(x ≤ 1) =.8413
Answers
If the random variable X is distributed normally with a mean of 0 and a standard deviation of 1, the probability P(x = 0) =.50 is not correct.
Probability refers to potential. A random event's occurrence is the subject of this area of mathematics. The range of the value is 0 to 1. Mathematics has included probability to forecast the likelihood of certain events. The degree to which something is likely to happen is basically what probability means.
The probability of all the events in a sample space adds up to 1.
Thus, If the random variable X is distributed normally with a mean of 0 and a standard deviation of 1, the probability P(x = 0) =.50 is not correct.
To know more about probability visit: brainly.com/question/30034780
#SPJ4
Can someone help me with this please

Answers
Answer:
C) The difference between the 75th and 25th percentiles is 12 inches.
Step-by-step explanation:
The interquartile range is the length of the "box" in a "box and whisker" plot. One end is the 25th percentile, and the other end is the 75th percentile. It is the difference between the maximum and minimum of the middle 50% of the data.
For the baker's loaf-length data set, the interquartile range being 12 inches means the loaves in the 75th percentile are 12 inches longer than the loaves in the 25th percentile. This could be described by choice C.
The _____ is commonly used to examine whether two groups are significantly different from each other.
Answers
T-test is commonly used to examine whether two groups are significantly different from each other or not.
A t-test is an inferential statistic used to determine if there is a significant difference between the means of two groups and how they are related. T-tests are used when the data sets follow a normal distribution and have unknown variances, like the data set recorded from flipping a coin 100 times.
It is a statistical test that is used to compare the means of two groups. It is often used in hypothesis testing to determine whether a process or treatment actually has an effect on the population of interest, or whether two groups are different from one another.
T-test is used to determine whether two groups are different or not.
For information on this, visit:
https://brainly.com/question/6589776
#SPJ4
The T-test is commonly used to examine whether two groups are significantly different from each other or not.
The T-test is an inference statistic used to determine whether two groups' means are significantly different and how they are related. The T-test is used when the data set is normally distributed and the variance is unknown, such as a data set recorded by tossing a coin 100 times. This is a statistical test used to compare the means of two groups. It is often used in hypothesis testing to determine whether a process or treatment actually affects a population of interest, or whether two groups differ from each other.A T-test is used to determine if two groups are different.
Learn more about T-test here
https://brainly.com/question/6589776
#SPJ4
Please answer this question

Answers
Answer: 14
Step-by-step explanation:
(3) (6) − (9) (2) + 8 + 6 (3) (6) − (9) (2) + 8 + 6 = 14
write the equation of the line that passes through (-8, -4) and (-6, -1) in slope-intercept form.

Answers
Answer: To write the equation of a line in slope-intercept form (y = mx + b), we need to find the slope (m) and y-intercept (b) of the line.
We can use the two given points (-8, -4) and (-6, -1) to find the slope:
m = (y2 - y1) / (x2 - x1)
m = (-1 - (-4)) / (-6 - (-8))
m = 3 / 2
Now that we have the slope, we can use either of the two given points to find the y-intercept:
y = mx + b
-1 = (3/2)(-6) + b
-1 = -9 + b
b = 8
Therefore, the equation of the line in slope-intercept form is:
y = (3/2)x + 8
Step-by-step explanation:
Use polar coordinates to find the limit. [If (r, #) are polar coordinates of the point (x, y) with r 2 0, note that r-o as (x, y) (0, 0).1 (If an answer does not exist, enter ONE) lim (x,-(0, 0) (x² + y²³) in(x² + y²) Need Help? Rodit
Answers
The limit as (x, y) approaches for the polar coordinates (0, 0) of (x² + y²)³ / (x² + y²) is 0.
To find the limit as (x, y) approaches (0, 0) of (x² + y²)³ / (x² + y²), we can rewrite the expression in polar coordinates.
In polar coordinates, x = r cos(theta) and y = r sin(theta), where r represents the radial distance and theta represents the angle.
Substituting these expressions into the limit expression, we have:
lim(r → 0) [(r² cos²(theta) + r² sin²(theta))³] / (r² cos²(theta) + r² sin²(theta))
Simplifying the expression inside the limit, we have:
lim(r → 0) (r² (cos²(theta) + sin²(theta)))³ / (r² (cos²(theta) + sin²(theta)))
The term (cos²(theta) + sin²(theta)) simplifies to 1, so we have:
lim(r → 0) (r²)³ / (r²)
lim(r → 0) \(r^{(2 * 3)\) / r²
lim(r → 0) \(r^{6\) / r²
lim(r → 0) \(r^{(6 - 2)\)
lim(r → 0) r⁴
As r approaches 0, the limit expression becomes 0⁴, which is equal to 0.
Therefore, the limit as (x, y) approaches (0, 0) of (x² + y²)³ / (x² + y²) is 0.
Learn more about polar coordinates at
https://brainly.com/question/31904915
#SPJ4
A _____________ is a line that provides an approximation of the relationship between the variables.
Answers
Answer:
srat
Step-by-step explanation:hehe i really dont know
The temperature is -3.5 degrees Fahrenheit at 7:00 am. During the next 4 hours, the temperature decreases by -15.5 degrees. What is the temperature at 11:00 am?
Answers
-4x(5x +1)
this needs to be written in polynomials
Answers
Answer:
-20x^2-4x
In mathematics, a polynomial is an expression consisting of variables and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. An example of a polynomial of a single indeterminate x is x² − 4x + 7.
Sofia cycled a total of 12 kilometers by making 4 trips to work. How many trips will Sofia have to make to cycle a total of 18 kilometers? Solve using unit rates.
Answers
Answer:
6 trips
Step-by-step explanation:
12 divided by 4 equals 3
18 divided by 3 equal 6
she will have to take six trips to drive 18 kilometers.
Find the total surface area of this cylinder. Give your answer to one decimal place first correct answer will get brainliest and 5 stars!!!

Answers
Answer:
The surface area formula is 2πr (h + r) where r and h are the radius and height respectively. Since π = 3.14, r = 7, h = 15 the answer is:
2 * 3.14 * 7 * (15 + 7) = 43.96 * 22 = 967.6
The makers of a soft drink want to identify the average age of its consumers. A sample of 35 consumers was taken. The average age in the sample was 21 years with a standard deviation of 6 years
a) Calculate the Margin of Error for a 97% level of confidence for the true average age of the consumers.
b) Determine a 97% confidence interval estimate for the true average age of the consumers.
c) Calculate the Margin of Error for a 90% level of confidence for the true average age of the consumers.
d )Determine a 90% confidence interval estimate for the true average age of the consumers.
e) Discuss why the 97% and 90% confidence intervals are different.
f) How large the sample must be in order to obtain 97% confidence interval with margin of error equal to 2 years (planning value for population standard deviation is 6)
Answers
a) Margin of error for 97% confidence: 2.55 years
b) 97% confidence interval: 18.45 to 23.55 years
c) Margin of error for 90% confidence: 1.83 years
d) 90% confidence interval: 19.17 to 22.83 years
e) The confidence intervals are different due to the variation in confidence levels.
f) Sample size required for 97% confidence interval with a margin of error of 2 years: at least 314.
a) To calculate the margin of error, we first need the critical value corresponding to a 97% confidence level. Let's assume the critical value is 2.17 (obtained from the t-table for a sample size of 35 and a 97% confidence level). The margin of error is then calculated as
(2.17 * 6) / √35 = 2.55.
b) The 97% confidence interval estimate is found by subtracting the margin of error from the sample mean and adding it to the sample mean. So, the interval is 21 - 2.55 to 21 + 2.55, which gives us a range of 18.45 to 23.55.
c) Similarly, we calculate the margin of error for a 90% confidence level using the critical value (let's assume it is 1.645 for a sample size of 35). The margin of error is
(1.645 * 6) / √35 = 1.83.
d) Using the margin of error from part c), the 90% confidence interval estimate is
21 - 1.83 to 21 + 1.83,
resulting in a range of 19.17 to 22.83.
e) The 97% and 90% confidence intervals are different because they are based on different levels of confidence. A higher confidence level requires a larger margin of error, resulting in a wider interval.
f) To determine the sample size required for a 97% confidence interval with a margin of error equal to 2, we use the formula:
n = (Z² * σ²) / E²,
where Z is the critical value for a 97% confidence level (let's assume it is 2.17), σ is the assumed population standard deviation (6), and E is the margin of error (2). Plugging in these values, we find
n = (2.17² * 6²) / 2²,
which simplifies to n = 314. Therefore, a sample size of at least 314 is needed to obtain a 97% confidence interval with a margin of error equal to 2 years.
To know more about statistics, visit:
https://brainly.com/question/19863416
#SPJ11
Which value is a solution of the inequality 2x − 3 < 9? A. x = −4 B. x = −3 C. x = −2 D. x = 3
Answers
Answer:
\(\huge\boxed{\sf x < 6}\)
Step-by-step explanation:
Given inequality:
2x - 3 < 9
Add 3 to both sides
2x < 9 + 3
2x < 12
Divide 2 to both sides
x < 6
\(\rule[225]{225}{2}\)
Answer:
Step-by-step explanation:
2x − 3 < 9
Solve:
2x − 3 < 9 <== add 3 to both sides
+ 3 + 3
2x < 12 <== divide both sides by 2, to isolate the variable (x)
/2 /2
x < 6
This means that x, can be any number than is smaller than (less than) 6.
A. x = −4
-5 < 6 <== correct
B. x = −3
-3 < 6 <== correct
C. x = −2
-2 < 6 <== correct
D. x = 3
3 < 6 <== correct
Therefore, all these are solutions to the inequality.
Hope this helps!

what’s the value of x or a

Answers
answer: x = 70 because of straight line theory. x+110=180
x=180-110
x= 70
Solve.
32 x 53
[?]
Hint: Remember to use order of operations.
first evaluate 32 and 5, and then multiply their values.
Enter
![Solve.32 x 53[?]Hint: Remember to use order of operations.first evaluate 32 and 5, and then multiply](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/CxS3aqTU1Ed82qcfB5AUbezZJySpSoTi.png)
Answers
Step-by-step explanation:
but 3^2 is 9
5^3 is 125
so the answer for this question 3^2 x 5^3 is 1,125
HELP PLEASE!!!!!!!!!!!!!!
Crystal has 94 compact discs that she wants to put into boxes. Each of the
boxes that she brought home holds 16 discs. How many of these boxes will
she need for all of her discs?
O A. 94 - b = 16
O B. 16b > 94
O C. 16b< 94
O D. b + 16 = 94
Answers
Answer:
16b > 94
Step-by-step explanation:
16b > 94
b > 5.875
Crystal needs 6 boxes to fit all 94 discs.
Find the area of a circle with diameter, d = 8.6m. Give your answer rounded to 1 DP.
Answers
Answer:
58.1 m²
Step-by-step explanation:
d = 8.6 m
r = d/2 = 4.3 m
A = πr²
A = 3.14159 × (4.3 m)²
A = 58.1 m²
3. Simplify:
(1-2)(¹-3) (1-4)-(1-99) (1-700)
Answers
(1-2)(¹-3) (1-4)-(1-99) (1-700) = (-1)(-2) (-2)-(1-99) (-699)
Simplifying further, we have:
(-1)(-2) = 2
(-2)-(1-99) = -2 - (-98) = 96
(-699) = -699
Putting it all together, we get:
2*96 - (-699) = 192 + 699 = 891
Therefore, the simplified expression is 891.
In which of the following situations would finding the surface area of an object be the most applicable?
Answers
Hi, you've asked an incomplete question. However, I provided a brief explanation about surface areas.
Explanation:
Surface area is a term commonly used in mathematics, and other branches of science, and it basically refers to a calculation of the total space that an object occupies.
For example, you can find the surface areas of a cuboid using the formula:
\(6s^{2}\) where s= side length.
Arlo has $25 to spend on a T-shirt and
shorts for gym class. The shorts cost $14.
Use the inequality 14 +1 < 25, where t
represents the cost of the T-shirt. What is
the most Arlo can spend on the T-shirt?
Answers
Arlo has $25 to spend on a T-shirt and
shorts for gym class. The shorts cost $14.
Use the inequality 14 +1 < 25, where t
represents the cost of the T-shirt. What is
the most Arlo can spend on the T-shirt?
the answer is $11.
A dragonfish is swimming at -900 m relative to sea
level. It rises 250 m. What is the dragonfish's new
depth relative to sea level? Show your work.
Answers
Answer:
-650
Step-by-step explanation:
Any point on the parabola can be labeled (x,y), as shown. What are the distances from the point (x,y) to the focus of the parabola and the directrix? Select two answers.distance to the focus: (squareroot over this whole problem)* (x+3)^2+(y-3)^2distance to the directix: |y-4|distance to the directix: |y+4|distance to the focus: *squareroot over again* (x+3)^2+(y-2)^2distance to the directix: |x-4|distance to the focus: *square root again* (x-2)^2+(y+3)^2

Answers
Given:
Vertex: (-3, 3)
Focus: (-3, 2)
Let's find the distance from the point (x, y) to the focus of the parabola and the directrix.
To find the distance, apply the distance formula:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)Thus, we have:
Distance from (x, y) to the focus:
Where:
(x1, y1) ==> (x, y)
(x2, y2) ==> (-3, 2)
Thus, we have:
\(\begin{gathered} d=\sqrt{(x-(-3))^2+(y-2)^2} \\ \\ d=\sqrt{(x+3)^2+(y-2)^2} \end{gathered}\)Therefore, the distance from the point (x, y) to the focus is:
\(\sqrt{(x+3)^2+(y-2)^2}\)• The distance from the point to the directrix.
From the graph, the directrix is:
y = 4
Now, to find the distance, subtract the y-coordinate of the point from y = 4.
The distance is the absolute value of the result.
Thus, we have:
\(|y-4|\)ANSWER:
Distance from the point to the focus:
\(\sqrt{(x+3)^2+(y-2)^2}\)Distance from the point to directrix:
\(|y-4|\)True or False, you need to convert mixed numbers into improper fractions first when multiplying mixed numbers?
Answers
Answer : the answer is true
NEED EXPLANATION & PROCESS
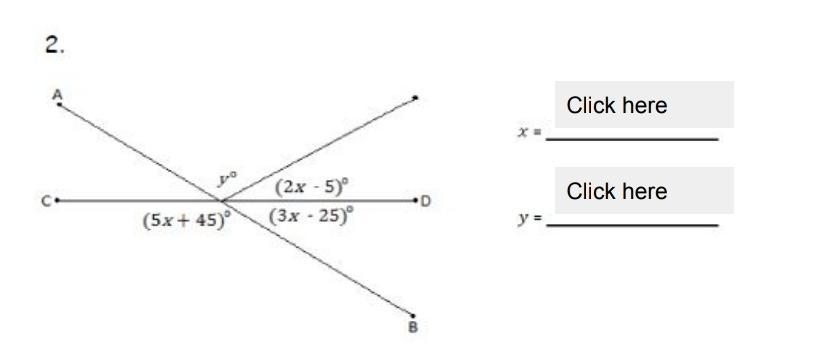
Answers
Answer:
x = 20, y = 110
Step-by-step explanation:
For x:
\(5x + 45 + 3x - 25 = 180\\8x + 20 = 180\\8x = 160\\x = 20\)
For y:
\(y + 2x - 5 + 3x - 25 = 180\\y + 2(20) - 5 + 3(20) - 25 = 180\\y + 40 - 5 + 60 - 25 = 180\\y + 35 + 35 = 180\\y + 70 = 180\\y = 110\)
PLEASE HELP ASAP!!!! ILL MARK BRAINLIEST

Answers
A graph of the solution of the inequality is: graph F.
What is an inequality?In Mathematics, an inequality can be defined as a mathematical relation that is typically used for comparing two (2) or more numerical data and variables in an algebraic equation based on any of the following inequality symbols:
Greater than (>).Greater than or equal to (≥).Less than (<).Less than or equal to (≤).Next, we would solve the given inequality by making x the subject of formula as follows;
x - 5 < 14
By adding 5 to both sides of the inequality, we have the following:
x - 5 + 5 < 14 + 5
x < 19
Note: The line on a number line should be open when the inequality symbol is greater than (>) or less than (<).
Read more on inequality here: brainly.com/question/27976143
#SPJ1

I need help with this question

Answers
Answer:
you can solve like this i think it is correct but i am not sure

What is the correct way to name the following image?

Answers
The correct way to name the image is Southwest Vector BA, indicating the direction of the vector from B to A.
How do we name the vector diagram?
Vector BA : This notation indicates that the vector starts at point B and ends at point A, and it is read as "vector B-A" or "B-A vector". The order of the letters reflects the direction of the arrow, from B to A.
Arrow SW or SW arrow: This notation indicates the direction of the vector, which is towards the southwest, and it is read as "arrow southwest" or "southwest arrow". The order of the letters reflects the direction of the vector, from the northwest to the southeast.
Southwest Vector BA : This notation combines both the direction and the points of the arrow, and it is read as "southwest vector B-A" or "B-A southwest vector". The order of the words reflects the direction of the vector, from the northwest to the southeast, and the order of the letters reflects the starting and ending points of the arrow.
Learn more about vector diagram here: https://brainly.com/question/19802988
#SPJ1
Given that f(x)=x^2=11x+30 and g(x)=x-5, find f(-g)(x) and express the result as a polynomial in simplest form.
Answers
Hey there,
We have,
f(x) = x² + 11x + 30g(x) = x + 6
Now,
(f.g)(x) = f(g(x))
Substituting...
g(x) = x + 6f(g(x)) = f(x + 6)
Now,
f(x + 6)= (x + 6)² + 11(x + 6) + 30= x² + 12x + 36 + 11x + 66 + 30= x² + 23x + 132
So,The value is x² + 23x + 132
Find the volume of the composite figures (pls)

Answers
For figure 1: ⇒ volume = 254.6 mi³
For figure 2: ⇒ volume = 1017.36 cubic cm
For figure 3: ⇒ volume = 864 m³
For figure 1:
It contains a cylinder,
Height = 7 mi
radius = r = 3 mi
And a hemisphere of radius = 3 mi
Since we know that,
Volume of cylinder = πr²h
And volume of hemisphere = (2/3)πr³
Therefore put the values we get ;
Volume of cylinder = π(3)²x7
= 197.80 mi³
And volume of hemisphere = (2/3)π(3)³
= 56.80 mi³
Therefore total volume = 197.80 + 56.80
= 254.6 mi³
For figure 2:
It contains a cylinder,
Height = 9 cm
radius = r = 6 cm
And a cone,
radius = 6 cm
Height = 5 cm
Volume of cylinder = π(6)²x9
= 1017.36 cubic cm
Volume of cone = πr²h/3
= 3.14 x 36 x 5/3
= 188.4 cubic cm
Therefore,
Total volume = 1017.36 + 188.4
= 1205.76 cubic cm
For figure 3:
It contains a rectangular prism,
length = l = 12 m
Width = w = 9 m
Height = h = 5 m
Volume of rectangular prism = lwh
= 12x9x5
= 540 m³
And a triangular prism,
Height = h = 6 m
base = b = 9 m
length = l = 12 m
We know that volume of triangular prism = (1/2) x b x h x l
= 0.5 x 9 x 6 x 12
= 324 m³
Total volume = 540 + 324
= 864 m³
To learn more about prism visit:
https://brainly.com/question/2918181
#SPJ1
What is the freezing point in c of a 0.33 m aqueous solution of Na2so3
Answers
The freezing point of a 0.33 m aqueous solution of Na₂SO₃ is -0.077 °C.
To find the freezing point of a solution, we can use the formula:
ΔTf = Kf · m
where ΔTf is the change in freezing point, Kf is the freezing point depression constant (for water, Kf = 1.86 °C/m), and m is the molality of the solution (in moles of solute per kilogram of solvent).
First, we need to calculate the molality of the solution:
m = moles of solute / mass of solvent (in kg)
We are given that the solution is 0.33 m, which means there are 0.33 moles of Na₂SO₃ per kilogram of water. The molar mass of Na₂SO is:
2 Na + 1 S + 3 O = 2(23.0 g/mol) + 32.1 g/mol + 3(16.0 g/mol) = 126.0 g/mol
So, 0.33 moles of Na₂SO₃ is equal to:
0.33 mol × 126.0 g/mol = 41.6 g
Since we have 1 kg of water, the mass of the solvent is 1000 g. Therefore, the molality of the solution is:
m = 41.6 g / 1000 g = 0.0416 mol/kg
Now, ΔTf = Kf · m = (1.86 °C/m) · (0.0416 mol/kg) = 0.077 °C
freezing point = 0 °C - ΔTf = 0 °C - 0.077 °C = -0.077 °C
Therefore, the freezing point of a 0.33 m aqueous solution of Na₂SO₃ is -0.077 °C.
Learn more about Freezing Point here:
https://brainly.com/question/3121416
#SPJ1
Answer: -1.84
Step-by-step explanation:
3x1.86x0.33=1.84
0.00-1.84= -1.84
late answer but hope it helps someone!