a landscaper is designing a park in the shape of a kite with a fountain in the center, F. AK = 28 ft, PF=48 ft and F=32 ft. He wants to install a walkway around the border of the park. The inside edge of the walkway will be edged with brick. The bricks are purchased in linear feet. How many linear feet of bricks should he purchaase?
Answers
Answer:
169.9
Step-by-step explanation:
Related Questions
7 friends share 840g of chocolate equally between them.
Felix thinks that each person gets 0.12kg.
Is he correct?
Write yes or no and explain how you know.
Answers
Answer:
he is definitely correct bcz u have to change the g into kg first then solve
plssss help me! A group of pet owners who only own a cat (C) or a dog (D) were asked which pet they owned. Drag and drop the missing outcomes in each box to show the possible results of asking 3 different pet owners. {DDD, DDC, Response area, DCC, CDD, Response area, CCD, CCC}
Answers
Answer:
CDC and DCD
Step-by-step explanation:
The first sequence rule is multiply by 3 starting from 5. The second sequence rule is add 9 starting from 18. What is the first number that appears in both sequences?
27
45
72
135
what is the answer
Answers
Considering the sequences given, the first number that appears in both sequences is given by: 45.
What numbers appear in the first sequence?The rule is multiply by 3 starting from 5, hence the numbers are:
(5, 15, 45, 135, ...).
What numbers appear in the second sequence?The rule is add 9 starting from 18, hence the numbers are:
(18, 27, 36, 45, ...).
45 is the first number that appeared in both sequences.
More can be learned about sequences at https://brainly.com/question/6561461
#SPJ1
Find the product 4 2/3 x 3 3/4
Answers
Answer:
45.6
Step-by-step explanation:
trust me bro(don't)
Answer:
17 1/2
Step-by-step explanation:
The quickest way is to put it as it improper fraction and then multiply it like normal.
For what value of 2 will the function f(x), be continuous at x=0?
(See Image) Thanks

Answers
(i) \(\lim_{x \to \pi/3}\) f(x) = 1 + √3.
(ii) \(\lim_{x \to \frac{\pi}{4}} f(x)\) does not exist.
For λ = 2.5, the function f(x) will be continuous at x = 0.
Given the function is,
f(x) = 1.5, when x = 0
= 1 -2 sin x, when x < π/4
= 1 + 2 sin x, when x > π/4
= 1 + (sin λx/sin 5x)
Now,
\(\lim_{x \to \pi/3}\) f(x) = \(\lim_{x \to \pi/3}\) (1 + 2 sin x) [Since, π/3 > π/4]
= 1 + 2 sin (π/3)
= 1 + 2√3/2 = 1 + √3
Hence, \(\lim_{x \to \pi/3}\) f(x) = 1 + √3.
Now left hand limit is,
\(\lim_{x \to \frac{\pi^+}{4}}\) f(x) = \(\lim_{x \to \frac{\pi^+}{4}}\) (1 + 2sin x) = 1 +2 sin(π/4) = 1 + 2*(1/√2) = 1 + √2
and right hand limit is,
\(\lim_{x \to \frac{\pi^-}{4}}\) f(x) = \(\lim_{x \to \frac{\pi^-}{4}}\) (1 - 2 sin x) = 1 - 2*(1/√2) = 1 - √2
Since left hand limit and right hand limit are not equal so value of \(\lim_{x \to \frac{\pi}{4}} f(x)\) does not exist.
\(\lim_{x \to 0}\) f(x) = \(\lim_{x \to 0}\) (1 + (sin λx/sin 5x)) = 1 + \(\lim_{x \to 0}\) ((sin λx/λx)/(sin 5x/5x))*(λ/5) = 1 + λ/5
Since f(x) is continuous at x = 0.
So, \(\lim_{x \to 0}\) f(x) = f(0)
1 + λ/5 = 1.5
λ/5 = 1.5 - 1 = 0.5
λ = 2.5
Hence the value of λ will be 2.5.
To know more about continuous here
https://brainly.com/question/27761372
#SPJ1
Which choice is equivalent to the expression below?
✓-27
A. -3✓3
B. 3✓3
C. 3i✓3
D. -✓27
E.-3✓3i
Answers
Answer:
C. 3i✓3
Step-by-step explanation:
Which choice is equivalent to the expression below?
✓-27
Square root of a negative value, so it will have a complex part.
We have that:
\(\sqt{-a^2} = ai\)
In this question:
The square root of -27 can be factored as:
\(\sqrt{-27} = \sqrt{3(-9)} = \sqrt{3}\sqrt{-9} = 3i\sqrt{3}\)
So the correct answer is given by option C.
PLS HELP FAST 20 POINTS + BRAINLIEST!!
Bacteria in a petri dish double the area they cover every day. If the dish is covered
after 16 days, on what day was only one quarter of it covered?
Answers
it doubles and is covered in 16 days so it is 32 in area (16 x 2 = 32)
A quarter of 32 = 8
So it would take 4 days to cover 8 (because 8/2=4)
Suppose that f and g are functions that are differentiable at x = 1 and that f(1) = 2, f '(1) = −1, g(1) = −2, and g'(1) = 3. Find h'(1). h(x) = (x2 + 8)g(x)
Answers
Answer:
\(h'(1) = 23\)
Step-by-step explanation:
Let be \(h(x) = (x^{2}+8)\cdot g(x)\), where \(r(x) = x^{2} + 8\). If both \(r(x)\) and \(g(x)\) are differentiable, then both are also continuous for all x. The derivative for the product of functions is obtained:
\(h'(x) = r'(x) \cdot g(x) + r(x) \cdot g'(x)\)
\(r'(x) = 2\cdot x\)
\(h'(x) = 2\cdot x \cdot g(x) + (x^{2}+8)\cdot g'(x)\)
Given that \(x = 1\), \(g (1) = -2\) and \(g'(1) = 3\), the derivative of \(h(x)\) evaluated in \(x = 1\) is:
\(h'(1) = 2\cdot (1) \cdot (-2) + (1^{2}+8)\cdot (3)\)
\(h'(1) = 23\)
For the following vectors, (a) find the dot product v•w ; (b) find the angle between v and w , (c) state whether the vectors are parallel, octagonal, or neither. V=-3i-4j, w=6i+8j
A- v•w
B-the angle between v and w is theta ^•?
C- the vectors v and w are?
Answers
B) The angle between vectors v and w can be found using the formula: cos(theta) = (v • w) / (||v|| ||w||), where ||v|| and ||w|| are the magnitudes of vectors v and w respectively.
First, we need to find ||v|| and ||w||:
||v|| = sqrt((-3)^2 + (-4)^2) = 5
||w|| = sqrt((6)^2 + (8)^2) = 10
Now, we can substitute in the values to get:
cos(theta) = (-50) / (5 * 10) = -1
theta = arccos(-1) = pi radians or 180 degrees.
Therefore, the angle between vectors v and w is 180 degrees.
C) Two vectors are parallel if their directions are the same, which can be determined by comparing their unit vectors.
The unit vector of v is:
v_hat = v / ||v|| = (-3/5)i + (-4/5)j
The unit vector of w is:
w_hat = w / ||w|| = (6/10)i + (8/10)j = (3/5)i + (4/5)j
We can see that the unit vectors are in opposite directions, which means that the vectors are anti-parallel or opposite. Therefore, the vectors v and w are neither parallel nor orthogonal.
If a=12 and h = 25, then the volume a triangular pyramid is?
Answers
The volume of the triangular pyramid, with a base area of 12 and a height of 25, is equal to 100 cubic units.
To calculate the volume of a triangular pyramid, we need the values of the base area and the height. Given that a = 12 and h = 25, we can proceed with the calculation.
The formula for the volume of a triangular pyramid is (1/3) * base area * height. Since we know the base area is equal to a, we can substitute the values into the formula.
Volume = (1/3) * a * h
Plugging in the given values, we have:
Volume = (1/3) * 12 * 25
Simplifying the expression further:
Volume = (1/3) * 300
Volume = 100
Therefore, the volume of the triangular pyramid, with a base area of 12 and a height of 25, is equal to 100 cubic units.
For more questions on volume
https://brainly.com/question/28298028
#SPJ11
givin the sequence
19,13,7,1
what is the 18 term of the sequence
A-71
B-77
C-83
D-89
Answers
The 18th term of the sequence is -83, the correct option is C.
What is arithmetic sequence?An arithmetic sequence is sequence of integers with its adjacent terms differing with one common difference.
If the initial term of a sequence is 'a' and the common difference is of 'd', then we have the arithmetic sequence as:
a, a + d, a + 2d, ... , a + (n-1)d, ...
Its nth term is
T_n = a + (n-1)d
(for all positive integer values of n)
And thus, the common difference is
T_{n+1} - T_n
for all positive integer values of n
Given:
The sequence=19,13,7,1...
n=18
D= 13-19
D= 6, a= 19
Now,
=a + (n+1)d
=19+(18-1)x-6
=-83
Therefore, the 18th term of the sequence will be -83
Learn more about arithmetic sequence here:
https://brainly.com/question/3702506
#SPJ1
10
The box-and-whisker plot below shows the distribution of the numbers of calories per serving for a selection of breakfast
cereals.
Breakfast Cereal Calories per Serving
50 65 80 95 110 125 140 155 170 185 200
Based on the box-and-whisker plot, what is the median number of calories per serving for the breakfast cereals?
110
B 120
125
135
Answers
The 125 is the median number of calories per serving for the breakfast cereals.
What is median?
The middle value in a sorted, ascending or descending list of numbers is known as the median, and it has the potential to describe a data set more accurately than the average does. It represents the midpoint of the data because it is the point above and below which half (50%) of the observed data falls.
Given:
The box-and-whisker plot below shows the distribution of the numbers of calories per serving for a selection of breakfast cereals.
We have to find the median.
Since median is the middle most number of the given list of numbers.
In the given list there are 11 numbers.
The middle most number is occur at 5th number.
The number on 5th place is 125.
Hence, the 125 is the median number of calories per serving for the breakfast cereals.
To know more about median, click on the link
https://brainly.com/question/14532771
#SPJ1
Help please
Driving on the highway, you can safely drive 70 miles per hour. Which of the following functions could be used to find how far you can drive in ‘h’ hours?
A.) D= 70/h. B.) D=70h. C.)h/70. D.)70+h
Answers
Answer:
B
Step-by-step explanation:
Explanation because that’s the answer
simplify 2 + 1/a / 2/a - a =
Answers
Answer:
\(-\frac{a^3-2a^2-2}{a^2}\)
Step-by-step explanation:
The size of a TV is determined by the length of the diagonal of the TV. A 42" TV means the length from one corner to the other is 42 inches. If the diagonal forms a 30 degree angle with the base of the TV, what are the height and width of the TV? *
Answers
Answer:
length = 5.38 feet
Step-by-step explanation:
All the eq. can be solved by Phythagoras's theorem
1) Diagonal is 70 inches, height is 42 inches so
70^2 = 42^2 + width^2
width ^2 = 3136, width = 56 inches
2) Base is 2 ft, length of ladder = hypotenuse = 10 ft
Height^2 = 10^2 -2^2 = 96
Height = 9.8 ft
3) Equilateral triangle has a side of 6
If you drop a vertical line from one corner of triangle to opposite side it bisects the side into equal parts. So the length of base is 3
The hypotenuse is 6
So height is sqrt (6*6 -3*3) = sqrt (27) = 3sqrt(3) = 5.2
4) Height = 12, width = 5
Diagonal^2 = 12*12 + 5*5 = 169
Diagonal = 13
5) Plant is 5 ft tall, distance from the ground is 2 ft
length ^2 = 5*5 + 2*2 = 29
length = 5.38 feet
The maximum weight M that can be supported by a beam is jointly proportional to its width w in inches and the square of its height h in inches and inversely proportional to its length L in feet. (a) Write an equation that expresses this proportionality. (Use k as the constant of proportionality.) (b) Determine the constant of proportionality if a beam 4 in. wide, 6 in. high, and 15 ft long can support a weight of 3840 lb. k
Answers
Answer:
M = kwh^2/L
k = 400
Step-by-step explanation:
Given that the maximum weight M that can be supported by a beam is jointly proportional to its width w in inches and the square of its height h in inches and inversely proportional to its length L in feet
Then
M ∝ wh^2/L
M = kwh^2/L
where k is the constant of proportionality
if a beam 4 in. wide, 6 in. high, and 15 ft long can support a weight of 3840 lb then
3840 = k * 4 * 6^2/15
k = 3840 * 15 / (4 * 36)
k = 400
f(x)=|x+8| How can function f be written as a piecewise function?
Answers
the absolute value function written as a piecewise function is:
f(x) = x + 8 if x ≥ -8
f(x) = -(x + 8) if x + < -8
How can this function be written as a piecewise function?
The absolute value function:
y = |x|
works as follows:
y = x if x ≥ 0.y = -x if x < 0.That is a piecewise function.
Now, in our case:
f(x) = |x + 8| can be rewritten to:
f(x) = x + 8 if (x + 8) ≥ 0
f(x) = -(x + 8) if (x + 8) < 0.
Now we should simplify the inequalities, so we get:
f(x) = x + 8 if x ≥ -8
f(x) = -(x + 8) if x + < -8
Here we have the absolute value function written as a piecewise function.
If you want to learn more about absolute value functions:
https://brainly.com/question/3381225
#SPJ1
8/4.9999998*9.38729371692756392837482983742983478938273894837289-6 777777/292723638x +992819% =129837/129387*928357-129378. ill do brainliets
Answers
Answer:
the final result of the mathematical expression is -129377.997350872.
Step-by-step explanation:
To solve this mathematical expression, we need to use the order of operations.The order of operations is a set of rules that dictate the sequence in which operations should be performed in a mathematical expression to get the correct result.Next, we should perform any multiplications or divisions, from left to right.Finally, we have a multiplication by +992819%, which gives us 0.0026491279400635046.The last part of the expression is 129837/129387*928357-129378, but since we have already completed all of the multiplications and divisions, we can simply perform the remaining addition and subtraction from left to right.This gives us a final result of -129378 + 0.0026491279400635046 = -129377.997350872.Therefore, the final result of the mathematical expression is -129377.997350872NO LINKS!! Part 8a: Please help me with this problem
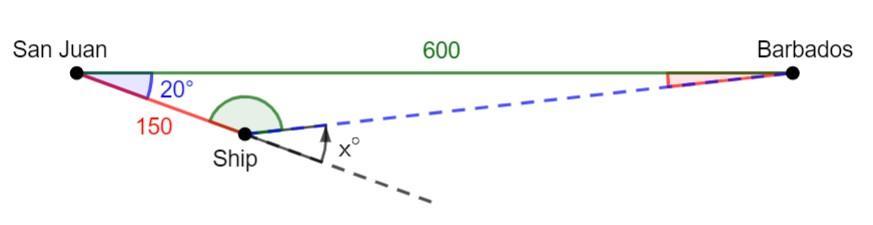
THIS IS NOT MULTIPLE CHOICE!!!
a. Through what angle should the captain turn to head directly to Barbados?
b. Once the turn is made, how long will it be before the ship reaches Barbados if the same 15-knot speed is maintained?

Answers
Answer:
26.38° (nearest hundredth)
30.7960166... hours = 30 hours 47 mins 37 secs
Step-by-step explanation:
one knot = one nautical mile (nm) per hour
Therefore, 15-knot speed for 10 hours = 15 × 10 = 150 nm
Use cosine rule to find the distance between the ship and Barbados (blue dashed line on attached diagram).
Cosine rule: c² = a² + b² - 2ab cos(C)
Given:
a = 150b = 600C = 20°⇒ c² = 150² + 600² - 2(150)(600)cos(20°)
⇒ c² = 213355.3283...
⇒ c = 461.9040249... nm
Use sine rule to calculate smallest missing angle (red on attached diagram)
\(\sf \implies \dfrac{sin(A)}{150}=\dfrac{sin(20)}{461.9040249}\)
\(\sf \implies sin(A)=\dfrac{150sin(20)}{461.9040249}\)
\(\sf \implies A=6.376917848... \textdegree\)
Sum of interior angles of a triangle = 180°
⇒ missing interior angle (green) = 180° - 20° - 6.376917848...° = 153.6230822...°
Angles on a straight line sum to 180°
⇒ x° = 180° - 153.6230822...° = 26.376917848...°
The distance between the Ship and Barbados is 461.9040249 nm
Therefore, to calculate the time, divide the distance by the speed:
t = 461.9040249... ÷ 15 = 30.7960166... hours
Nina skated for 2 hours and 14 min she stop at 8:24 pm when did Nina start skating
Answers
Answer:
6:10
Step-by-step explanation:
what is the answer this math problem?

Answers
Answer:
HLO Mate here is ur answer

How many solutions does this system have? no solutions one unique solution O O two solutions O or an infinite number of solutions

Answers
Answer:
no solutions
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
equation of blue line is y = x + 2 , in slope- intercept form
with slope m = 1
equation of red line is y = x - 3 , in slope- intercept form
with slope m = 1
• Parallel lines have equal slopes
then the blue and red lines are parallel.
the solution to the system is at the point of intersection of the 2 lines
since the lines are parallel then they do not intersect each other.
thus the system shown has no solution.
A concession stand charges $5.75 for 5 muffins. What is the cost per muffin?
A
$1.00
B
$1.15
С
$28.75
D
$10.75
Answers
Answer:
B- $1.15
Step-by-step explanation:
5.75 divided by 5 equals 1.15
Solve
Plsss helpppppp

Answers
Answer:
∠L = 51°
Hope this helps!
Step-by-step explanation:
Alternate exterior angles theorem
what is the cordinates of point A
no flile or link or i will be report you

Answers
Answer:
Um it’s (1,0) right?
Step-by-step explanation:
2. Use this value to estimate the size of a crowd that is 10 feet deep on both sides of the street
standing along a 1-mile section of a parade route. There is 5,280 feet in 1 mile.
Answers
Answer: 50000 feet
Step-by-step explanation:
Help please:)
Graph the equation by plotting points.
X=4
Answers
Answer:
(4,0)
Step-by-step explanation:
You basically are plotting a point on the positive number 4 on the x line. Since they're only asking for an X and not a Y, you'd leave it as (4,0). Hope this helps!
A country’s daily oil production can be approximated by q(t)=0.013t^2-0.6t+5.27
Answers
and y = -8 when x = 20, find "y" if x = -4.
Enter the number that belongs in the green box.
Reduce to simplest form.
PLEASE HELP!!!!!!
The box plot displays the number of flowers planted in a town last summer.
10
Flowers Planted In Town
13 14 15 16 17 18 19 20 21 22 23 24
Number of Flowers
Which of the following is the best measure of center for the data shown, and what is that value?
O The mean is the best measure of center and equals 12.
O The mean is the best measure of center and equals 10.
The median is the best measure of center and equals 12.
30 31
The median is the best measure of center and equals 10.
Answers
The best measure of center for the data shown is the median, and its value is 17.
The median is the best measure of center for the given data set. To find the median, we arrange the numbers in ascending order:
10, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24
Since the data set has an odd number of values, the median is the middle value, which in this case is 17.
Therefore, the best measure of center for the data shown is the median, and its value is 17.
Learn more about Box plot here:
https://brainly.com/question/9827993
#SPJ1
Which is the graph of g(x)=[x+3
Answers
The graph of the function g(x) = x + 3 is a straight line that passes through the point (0, 3) on the y-axis and has a slope of 1.
To understand how to plot the graph, let's consider a few points on the line.
We can choose any values for x and calculate the corresponding values for g(x).
Let's start with x = 0.
Substituting this value into the function, we get g(0) = 0 + 3 = 3.
So, the point (0, 3) is on the graph.
Next, let's choose x = 1.
Substituting this value into the function, we get g(1) = 1 + 3 = 4.
This gives us another point on the line, (1, 4).
Similarly, we can choose more values for x and calculate the corresponding values for g(x).
For example, if we let x = -1, we get g(-1) = -1 + 3 = 2, giving us the point (-1, 2).
By connecting these points and extending the line in both directions, we obtain a straight line that represents the graph of g(x) = x + 3.
The line has a positive slope of 1, which means it rises by 1 unit vertically for every 1 unit it moves horizontally.
Overall, the graph of g(x) = x + 3 is a straight line that passes through the point (0, 3) and has a slope of 1.
For similar question on function.
https://brainly.com/question/29631554
#SPJ8
