A large car company states that the brake system will function properly for 5.3 years with a population standard deviation of 0.9 years before needing maintenance. An independent research facility is concerned that the brake systems may not last as long as the company claims. They took a random sample of 40 cars made by the manufacturer and found the average to be 4.1 years. Based on ? = 0.01, what is the correct conclusion for the hypothesis test?
Answers
Since the calculated t-value (t = -7.95) is less than the critical t-value (-2.704), we reject the null hypothesis and conclude that there is sufficient evidence to suggest that the brake systems do not last as long as the car company claims.
We can set up the null and alternative hypotheses as follows:
H0: μ = 5.3 (the brake systems last as long as the company claims)
H1: μ < 5.3 (the brake systems do not last as long as the company claims)
Here, we want to test the hypothesis at a significance level of α = 0.01.
To conduct the hypothesis test, we can use a one-sample t-test with the test statistic:
t = (X - μ) / (s / sqrt(n))
where X is the sample mean (4.1), μ is the population mean (5.3), s is the sample standard deviation (0.9), and n is the sample size (40).
Plugging in the values, we get:
t = (4.1 - 5.3) / (0.9 / sqrt(40)) = -4.38
Using a t-distribution table with degrees of freedom (df) = n - 1 = 39, we find the critical t-value for a one-tailed test with α = 0.01 to be -2.423.
Since our calculated t-value (-4.38) is less than the critical t-value (-2.423), we reject the null hypothesis and conclude that there is sufficient evidence to support the claim that the brake systems do not last as long as the company claims.
To know more about hypothesis,
https://brainly.com/question/17030065
#SPJ11
Related Questions
determine whether the following graph represent a function.
1. one to one function
2. function but not one to one
3. not a function

Answers
What is the ratio in simplest form between the length of a side in ABCD and the length of its corresponding side in WXYZ? A. B. C. D.

Answers
Answer:
The Answer would be C) 3/4
Step-by-step explanation:
If you subtract a quarter of the number presented on right left hand on the picture you get the numbers presented on the left hand side of the picture shown. There fore the ratio is 3/4 or three quarters of the already existing number.
Answer:
Step-by-step explanation:

In the diagram below, if side AB = 21, BC = 15, AC = 9, DE = 7, EF = 5, and DF = 3 then we can say that ___.
he two triangles are similar by SAS
b.
the two triangles are not SSS
c.
the two triangles are congruent
d.
the two triangles are similar by SSS
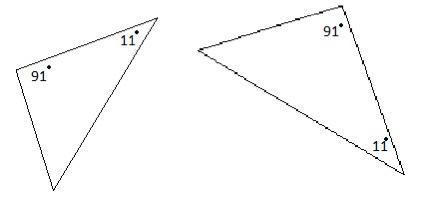
Answers
Answer: B. the two triangles are not Side-side-side
From the diagram, the two triangles are similar based on the angle-angle similarity theorem.
What is an equation?An equation is an expression that shows the relationship between two or more variables and numbers.
Two triangles are said to be similar if they have the same shape and the ratio of their corresponding sides are in the same proportion.
From the diagram, the two triangles are similar based on the angle-angle similarity theorem.
Find out more on equation at: https://brainly.com/question/13763238
#SPJ1
A straight line PQ passing through points (1,-6) and (6, 14). Determine whether a straight line which passing through (-4,-8) and (-1,7) is parallel to PQ. Explain your answer. [3 markah / marks)
Answers
Answer:
line not parallel to PQ
Step-by-step explanation:
Parallel lines have equal slopes
Calculate slopes m of both lines using slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (P (1, - 6) and (x₂, y₂ ) = Q (6, 14 )
\(m_{PQ}\) = \(\frac{14-(-6)}{6-1}\) = \(\frac{14+6}{5}\) = \(\frac{20}{5}\) = 4
Repeat with (x₁, y₁ ) = (- 4, - 8 ) and (x₂, y₂ ) = (- 1, 7 )
m = \(\frac{7-(-8)}{-1-(-4)}\) = \(\frac{7+8}{-1+4}\) = \(\frac{15}{3}\) = 5
Since slopes are not equal then lines are not parallel
PLS HELP MEEEEE!!!!!!!

Answers
Answer:
i think true hehehehehehehhehehehehe
Answer:
True
Step-by-step explanation:
Some people think a long drought may have occurred. However this information is not proven.
Find the value of the given expression.
(see the image)

Answers
Answer:
d. 14
Step-by-step explanation:
3(2) = 3 × 2 = 6Plug 6 in: 12 + {10 ÷ [11 - 6]}11 - 6 = 5Plug 5 in: 12 + {10 ÷ 5}10 ÷ 5 = 2Plug 2 in: 12 + 212 + 2 = 14I hope this helps!
If the factors of quadratic function g are (x-7) and (x+3) what are the zeros of function 9
Answers
Answer: the zeros are x = 7, -3
Step-by-step explanation:
find the future value of $750 deposited each month at 3.25% for 15 years
Answers
Answer:
P=1538.461
Step-by-step explanation:
do it by the formula of
I=PRT, I=750 R=3.25% T=15
Find the average rate of change of y=0.5x-3 over the interval -3(equal to or <)x(equal to or <)4
Answers
The value of average rate of change of y = 0.5x - 3 over the interval
- 3 ≤ x ≤ 4 is, 0.5.
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
We have to given that;
The function is,
⇒ y = 0.5x - 3
Now, The average rate of change is,
⇒ y = 0.5x - 3
⇒ dy / dx = 0.5
Hence, The value of average rate of change of y = 0.5x - 3 over the interval - 3 ≤ x ≤ 4 is, 0.5.
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
Joey invests in a CD where he will earn 5.5%
simple interest. If he deposits $1,400 in the
account, what will his total, including the
interest, be after 6 months?
Answers
I=PRT
I=1400*0.055*0.5
I=$38.50
Now add the principle and the interest
$1400+$38.50
$1438.50
Find a value of c so that P(Z ? c) = 0.71. a) -1.11 b) 0.75 c) -0.55 d) 0.55 e) 1.55
Answers
Among the provided answer options, the closest value to -0.555 is -0.55, which is option c. Therefore, option c (-0.55) is the value of c that satisfies P(Z ? c) = 0.71.
The notation P(Z ? c) represents the probability that a standard normal random variable Z is less than or equal to c. To find the value of c that corresponds to P(Z ? c) = 0.71, we need to determine the Z-score associated with this probability.
Using a standard normal distribution table or a calculator, we can find that a Z-score of approximately 0.555 corresponds to a cumulative probability of 0.71. However, since we are looking for the value of c in P(Z ? c), we need to consider the opposite inequality.
Learn more about probability here:
https://brainly.com/question/14210034
#SPJ11
Choose from the drop-down menus to match the trigonometric expression with its value. Sine StartFraction 2 pi Over 5 EndFraction cosine StartFraction pi Over 10 EndFraction + cosine StartFraction 2 pi Over 5 EndFraction sine StartFraction pi Over 10 EndFraction = Cosine 13 degrees cosine 47 degrees minus sine 13 degrees sine 47 degrees = Sine StartFraction 2 pi Over 5 EndFraction cosine StartFraction 8 pi Over 5 EndFraction + cosine StartFraction 2 pi Over 5 EndFraction sine StartFraction 8 pi Over 5 EndFraction =
Answers
Answer:
1
0.5
0
Step-by-step explanation: got it right on edge
Answer:
1
0.5
0
Step-by-step explanation:
just took it
I have to write the equation in slope intercept form and my question is. Containing (2, -1) and (-3,-1)
Answers
First lets define what is the equation of a line:
equation of a line is
y=mx +b
So, equation in slope intercept form would be y=mx +b
To calculate the slope m we would have to use the points (2, -1) and (-3,-1) and calculate the following formula:
slope= y2-y1/x2-x1
slope=-1+1/-3-2
slope=0
Therefore, equation in slope intercept form would be for points x -1 and y -1 would be:
-1=0*-1 + b
-1=b
Hence, y= -1
what is the difrence between domain and range
Answers
Answer:
Domain is the set of all possible input values is any relation. It means the output value in a function depends upon each member of domain. Domain value vary in different mathematical problems and depends upon the function for which is it solved. If we talk about cosine, then domain is the set of all possible real numbers either above the 0 value or below the 0 value, it could also be 0. While for square root, the domain value could not be less than 0, it should be minimum 0 or above 0. In other words, you can say that domain of square root is always 0 or positive value. For complex and real equations, the domain value is a subset of complex or real vector space. If we want to solve a partially differential equation for finding the value of domain, then your answer should lie within three dimensional space of Euclidean geometry.
Step-by-step explanation:
Solve the system of equations
2x−9y=14
x=−6y+7
x, equals ?
y, equals ?
Answers
Answer:
x = 7
y = 0
Step-by-step explanation:
use substitution method:
2(-6y + 7) - 9y = 14
-12y + 14 - 9y = 14
-21y = 0
y = 0
x = -6(0) + 7
x = 7
Step-by-step explanation:
Hey there!
Given eqautions are;
2x-9y= 14……………(i)
x= -6y+7………………(ii)
~ Putting the value of"x" from eqaution (ii) in eqaution (i).
2(-6y+7) - 9y = 14
~ Simplify it.
-12y +14 -9y= 14
21y = 0
y =0/21
Therefore, y= 0.
Now,
~ Put value of "x" on eqaution (ii).
X = -6(0)+7
x= (0)+7
x= 7
Therefore, x= 7.
Check:
Putting the value of X and y in eqaution (ii)
7= -6(0)+7
7=7(True).
x= 7
y= 0
Hope it helps....
A pool with a square bottom is to have a volume of 2000 cubic feet. The owners plan to use a fancy tile to complete the pool. The sides of the pool will cost $80 per square foot and the bottom of the pool will cost $40 per square foot. Find the pool dimensions that will minimize the cost of construction.
Answers
Considering the given conditions in the question, the dimensions that will minimize the cost of construction of the pool are:
base length = 10 feet
base width = 10 feet
pool depth = 20 feet
Volume of a material implies the maximum amount of substance that it can contain.
From the given question, it is expected that the pool would have the shape of a cuboid, thus its volume can be determined by:
volume of the pool = length x width x height
= base area x height
Thus, given that the volume of the pool is 2000 cubic feet, then;
2000 = base area x height
i. Let the dimensions of the square base be 10 feet, and its height 20 feet, so that;
volume = 10 x 10 x 20
= 2000 cubic feet
The cost of constructing the pool of the assumed dimensions would be:
Total area of its sides = 4 x 200
= 800 square feet
The cost of tiling the sides of the pool = $80 x 800
= $ 6400.0
Area of the base of the pool = 10 x 10
= 100 square feet
The cost of tiling the base of the pool = $40 x 100
= $4000
Total cost = $6400 + $4000
= $10400
Total cost of constructing the pool with the assumed dimensions is $10400.
ii. Let the dimensions of the square base be 20 feet, and its height 5 feet, so that;
volume = 20 x 20 x 5
= 2000 cubic feet
The cost of constructing the pool of the assumed dimensions would be:
Total area of its sides = 4 x 100
= 400 square feet
The cost of tiling the sides of the pool = $80 x 400
= $ 32000
Area of the base of the pool = 20 x 20
= 400 square feet
The cost of tiling the base of the pool = $40 x 400
= $16000
Total cost = $16000 + $32000
= $48000
Total cost of constructing the pool with the assumed dimensions is $48000.
Therefore, the dimensions that will minimize the cost of construction of the pool are:
base length = 10 feet
base width = 10 feet
pool depth = 20 feet
Visit: https://brainly.com/question/16955358
Jamie baked cookies to give to her friends. She gave 3 cookies to Anna and gave Elle 5 more than twice what was given to Anna. She gave half of what she had left to her best friend Grace. She now has 10 cookies. How many cookies did Jamie have to begin with?A. 18 B. 24 C. 30 D. 34
Answers
Jamie had 34 cookies to begin with. Let's use the information given to create an equation to solve for the number of cookies Jamie had to begin with:
Jamie gave 3 cookies to Anna, so she had x - 3 cookies left.
Elle received 5 more than twice what Anna received, so she received 5 + 2(3) = 11 cookies.
This means Jamie had x - 3 - 11 = x - 14 cookies left.
Half of what she had left was given to Grace, so she gave (x - 14)/2 cookies to Grace.
She now has 10 cookies, so:
x - 3 - 11 - (x - 14)/2 = 10
Simplifying this equation, we get:
2x - 44 = 40
2x = 84
x = 42
Therefore, Jamie had 42 cookies to begin with.
The answer is not one of the options given, but the closest option is (D) 34 . However, this is not the correct answer.
Learn more about cookies :
https://brainly.com/question/26252639
#SPJ4
For a two-tailed test at 12. 66% significance level, the critical value of z is:.
Answers
for a two-tailed test at a 12.66% significance level, the critical values of z are approximately +1.53 and -1.53. We are looking for the z-score that corresponds to the area to the right of it (for the positive critical value) equal to 0.0633.
For a two-tailed test at a 12.66% significance level, we need to find the critical value of z.
Step 1: Determine the significance level for each tail.
Since this is a two-tailed test, we need to divide the overall significance level (12.66%) by 2. This gives us 6.33% (or 0.0633 in decimal form) in each tail.
Step 2: Find the z-score associated with the given significance level.
To find the critical value of z, you can use a z-table or an online calculator. We are looking for the z-score that corresponds to the area to the right of it (for the positive critical value) equal to 0.0633.
Using a z-table or calculator, you'll find that the z-score is approximately ±1.53.
So, for a two-tailed test at a 12.66% significance level, the critical values of z are approximately +1.53 and -1.53.
To know more about z-score Visit:
https://brainly.com/question/15016913
#SPJ11
A sculptor cuts a pyramid from a marble cube with volume
t3 ft3
The pyramid is t ft tall. The area of the base is
t2 ft2
Write an expression for the volume of marble removed.
Answers
The expression for the volume of marble removed is (2t³/3).
The given information is as follows:
A sculptor cuts a pyramid from a marble cube with volume t^3 ft^3
The pyramid is t ft tall
The area of the base is t^2 ft^2
The formula to calculate the volume of a pyramid is,V = 1/3 × B × h
Where, B is the area of the base
h is the height of the pyramid
In the given scenario, the base of the pyramid is a square with the length of each side equal to t ft.
Thus, the area of the base is t² ft².
Hence, the expression for the volume of marble removed is given by the difference between the volume of the marble cube and the volume of the pyramid.
V = t³ - (1/3 × t² × t)V
= t³ - (t³/3)V
= (3t³/3) - (t³/3)V
= (2t³/3)
Therefore, the expression for the volume of marble removed is (2t³/3).
Learn more about volume of pyramid:
https://brainly.com/question/17615619
#SPJ11
help me with my math assignment for 25 points and crown.


Answers
The dimensions and volumes of the various containers that can be ,made with the 3 meters × 3 meters sheet of fine wire indicates that the maximum volume possible is 2 m³
What is the volume of a rectangular prism container?The volume of a rectangular prism container is the product of the base area and the height of the container.
The volume of the open-topped container formed by the 3 m × 3 m sheet of fine wire mesh can be presented as follows
Step 1:
\(\begin{tabular}{|c|c|c|c|c|c|} \cline{1-5}Corner cut (m) & Length (m)&Width (m)&Height(m)&Volume (m^3) \\ \cline{1-5}0& 3&3&0&0 \\ \cline{1-5}0.5 & 2&2&0.5&2 \\ \cline{1-5} 1& 1&1&1&1 \\ \cline{1-5} \cline{1-5}\end{tabular}\)
Step 2; Let x represent the corner cut
Step 3; The expression for the new side length can be found as follows;
When x is cut from each corner, the new side length is; 3 - 2·x
Step 4: The expression for the volume can be obtained from the volume of a cube formula, which is; V = L × W × H
Where;
L = The length of the box = 3 - 2·x
W = The width of the box = 3 - 2·x
H = The height of the box = x
Therefore, the volume of the container is; x·(3 - 2·x)²
Step 5: Please find attached the graph of the volume function created with MS Excel
Step 6; The value of the volume cut that generates the (optimal) maximum volume, obtained from the graph is; x = 0.5
Step 7 The values in the table indicates that when x = 2, the volume will be 3 m³, which is the maximum volume.
Learn more on optimization of a function here: https://brainly.com/question/15358878
#SPJ1

Points A and B have the coordinates shown below.
Estimate the length of AB to the nearest tenth of a unit.
A= (-4,7)
B= (-12, -10)
AB = units
Answers
Answer:
Distance AB is 18.79 units
Step-by-step explanation:
Given two points with coordinates as:
A= (-4,7)
B= (-12, -10)
To find:
Distance AB = ?
Solution:
To find the distance between two points with given coordinates, we can use Distance formula.
Distance formula is given as:
\(D = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
where \((x_1, y_1)\) and \((x_2, y_2)\) are the two coordinates whose distance is to be find out.
\(x_1 = -4\\y_1 = 7\\x_2 = -12\\y_2 = -10\)
\(AB = \sqrt{(-12-(-4))^2+(-10-7)^2}\\\Rightarrow AB = \sqrt{(-8)^2+(-17)^2}\\\Rightarrow AB = \sqrt{64+289}\\\Rightarrow AB = \sqrt{353}\\\Rightarrow \bold{AB = 18.79\ units }\)
Distance AB is 18.79 units
Answer:
AB = 18.8 units
Step-by-step explanation:
If there are two points (x1,y1) and (x2,y2) on the coordinate plane.
distance between those two points = \(\sqrt{(x1-x2)^{2} + (y1-y2)^{2} }\)
given points are
A= (-4,7)
B= (-12, -10)
\(AB = \sqrt{(-4 -(-12))^{2} + (7-(-10))^{2} }\\AB = \sqrt{(-4 +12)^{2} + (7+10)^{2} }\\AB = \sqrt{(8)^{2} + (17)^{2} }\\AB = \sqrt{64 + 289 }\\AB = \sqrt{353 }\\AB = 18.79\)
Thus, length of AB is 18.79 units
since, value of hudredth of unit is 9 which is greater than 9 then rounding the value to nearest tenth of unit we increase the value at tenth of unit place by that is 7 becomes 8
length of AB to the nearest tenth of a unit is 18.9 units
Given the following returns, what is the variance? Year 1 = 16%; year 2 = 6%; year 3 = -25%; year 4 = -3%.
.0268
.0344
.0306
.0297
.0209
Answers
The supplied returns' variance is around 0.02495.
To calculate the variance, we need to follow these steps:
Step 1: Calculate the average return (mean) of the given returns.
Step 2: Calculate the squared differences between each return and the mean.
Step 3: Calculate the average of the squared differences, which gives us the variance.
Let's perform these calculations:
Step 1:
Average return (mean) = (16% + 6% - 25% - 3%) / 4 = -6%
Step 2:
Squared differences:
(16% - (-6%))² = (22%)² = 0.0484
(6% - (-6%))² = (12%)² = 0.0144
(-25% - (-6%))² = (-19%)² = 0.0361
(-3% - (-6%))² = (3%)² = 0.0009
Step 3:
Average of the squared differences:
(0.0484 + 0.0144 + 0.0361 + 0.0009) / 4 = 0.0998 / 4 = 0.02495
Therefore, the variance of the given returns is approximately 0.02495.
Learn more about Variance on:
https://brainly.com/question/15707019
#SPJ11
you are taller than your sister, your sister is taller than your mother, therefore you are taller than your mother. this is an example of
Answers
The statement, "you are taller than your sister, your sister is taller than your mother, therefore you are taller than your mother" is an example of transitive property of inequality. Transitive property of inequality states that if a is greater than b and b is greater than c, then a is greater than c.
In the given example, a represents "you," b represents "your sister," and c represents "your mother." Therefore, according to the transitive property of inequality, if you are taller than your sister and your sister is taller than your mother, then you are taller than your mother.
As for writing more than 100 words about the transitive property of inequality, this property is a fundamental concept in mathematics that is used to compare numbers and determine the order of numbers.
To know more about inequality visit:
https://brainly.com/question/20383699
#SPJ11
Kristen invested $14763 in an account at an annual interest rate of 3.4%. She made no deposits or withdrawals on the account for 5 years. The interest was compounded annually. Find the balance in the account, to the nearest whole number, at the end of 5 years.
Answers
$17,449.27
Step-by-step explanation:Interest is the amount of money earned on an account.
Compound Interest
Interest rate is the percentage at which the account earns interest. For this account, the interest rate is 3.4%. Compound interest is when the amount of interest made increases over time. In the question, we are told that the interest on the account is compounded once every year. This means that the amount of interest earned increases once a year. We can use a compound interest formula to solve for the balance in the account in 5 years.
Solving Compound Interest
The compound interest formula is:
\(\displaystyle A = P(1+\frac{r}{n})^{n*t}\)In this formula, P is the principal (initial investment), r is the interest rate in decimal form, n is the number of times compounded per year, and t is the time in years. Now, we can plug in the information we know and solve for the final balance.
A = 14763( 1 + 0.034)⁵A = 17,449.27This means that after 5 years, the balance in the account will be $17,449.27.
Amelia went to an amusement park with $45 to spend. She bought lunch for $10.25 and paid $5.00 for each ride. What is the greatest number of rides Amelia could ride?
Answers
Answer:
Your answer is $34.75
Step-by-step explanation:
plz mark me brainliest
Answer:
6
Step-by-step explanation:
what is a decrease of £264 by39%
Answers
What are the slope and the y-intercept of the linear function that is represented by the graph? On a coordinate plane, a line goes through points (0, 3) and (4, 0). The slope is Negative four-thirds, and the y-intercept is 3. The slope is Negative four-thirds, and the y-intercept is 4. The slope is Negative three-fourths, and the y-intercept is 3. The slope is Negative three-fourths, and the y-intercept is 4. Mark this and return
Answers
The slope of the linear equation is -3/4 and the y-intercept is 3.
What are the slope and y-intercept of the line?A general linear equation is written as:
y = a*x + b
Where a is the slope and b is the y-intercept.
If a line passes through the points (x₁, y₁) and (x₂, y₂), then the slope is:
a = (y₂ - y₁)/(x₂ - x₁)
Here the line passes through (0, 3) and (4, 0), the slope is:
a = (0 - 3)/(4 - 0) = -3/4
And because of the point (0, 3) we know that the y-intercept is 3.
Learn more about linear equations at:
https://brainly.com/question/1884491
#SPJ1
The scatter plot shows the earnings of Walter after working his shifts of varying hours each day. Which equation represents the line of best fit?
A)y= -16.670 +1.89
B)y= -15.16x + 15.26
C) y= 15.0 + 3
D)y= 16.67x + 3.33

Answers
Answer:
try D
Step-by-step explanation:
it's the closest I could get on Desmos
Answer:
D.
Step-by-step explanation:
Can someone plz help me asap, thank you?!

Answers
Please help.. I don’t understand the problem

Answers
Answer:
answer is 50.
Hope that it is helpful. Vote and like me