A line passes through (−1, 7) and (2, 10). Which answer is the equation of the line?
Answers
Answer:
Is there multiple choice?
Step-by-step explanation:
I'll edit this
Related Questions
Some data have a distribution that is symmetric and bell-shaped, a mean value of 5.5. We know that 95% of the data is between 4.3 and 6.7. Use the 95% rule to find the standard deviation.
Answers
Answer:
The standard deviation σ = 0.6122
Step-by-step explanation:
Explanation:-
Given mean of the Population = 5.5
we know that 95% of confidence interval of Z-score = 1.96
95% of confidence interval for mean in normal distribution
(μ±Z₀.₉₅σ)
(μ - 1.96σ , μ +1.96σ)
given that 95% of confidence interval between 4.3 and 6.7
μ - 1.96σ = 4.3
5.5 -1.96σ = 4.3
5.5 - 4.3 = 1.96σ
1.2 = 1.96σ
σ = \(\frac{1.2}{1.96}\)
The standard deviation σ = 0.6122
if x=2,and y=-3 then xy^2
Answers
Given the expression:
\(xy^2\)if x = 2, and y = -3, then we have the following:
\(\begin{gathered} x=2 \\ y=-3 \\ \Rightarrow xy^2=(2)(-3)^2=(2)(9)=18_{} \end{gathered}\)therefore, the final result is 18
Comparing Two Linear Functions Use the graph and table to answer the questions. Which vehicle loses the most value each year? Car: 20 000 (2. 16500) 15 000 (G, 10900) Which vehicle will lose all of its value first? Value ($) 10.000 5000 6 8 If the truck's rate of depreciation changes to a decrease of $1,650 each year, which vehicle will lose all of its value first? Years Truck: Years: x Value ($) y 21,000 3 17,700 6 14.400

Answers
Answer:
Use the graph and table to answer the questions.
Which vehicle loses the most value each year?
Car
Which vehicle will lose all of its value first?
Car
If the truck’s rate of depreciation changes to a decrease of $1,650 each year, which vehicle will lose all of its value first?
Truck
Step-by-step explanation:
Answer:
car car truck
Step-by-step explanation:
CAN SOMEONE PLEASE HELP ME??!!

Answers
Answer:
Step-by-step explanation:its ratxrat
...
The zeros of the divisor,
x-3=0,x=3
f(3)=4(3)²-3-3=30
The remainder is 30
A data set includes 108 body temperatures of healthy adult humans having a mean of 98.2 and a standard deviation of 0.64 . Construct a 99% confidence interval estimate of the mean body temperature of all healthy humans . What does the sample suggest about the use of 98.6 as the mean body temperature.?
Answers
The 99% confidence interval for mean temperature of human is :
( 98.04f, 98.40f )
A data set includes 108 body temperatures of healthy adult humans having a mean of 98.2 and a standard deviation of 0.64 .
Now, We have to construct a 99% confidence interval estimate of the mean body temperature of all healthy humans.
We use these formula for upper limit and lower limit:
u = x + Zα/2 × (s/√n) (For the upper limit)
u = x - Zα/2 × (s/√n) (For the lower limit)
We have the information from question:
x = sample mean = 98.2
s = standard deviation = 0.64
n = sample size = 108.
\(Z_\frac{\alpha }{2}\) = critical value for a 2 tailed test performed at a 1% level of significance ( 100% - 99%) = 2.58
Now, Substitute the parameter,
For upper limit:
u = x + Zα/2 × (s/√n)
u = 98.2 + 2.58 ( 0.64/√108)
u = 98.2 + 2.58 ( 0.0616)
u = 98.2 + 0.1589
u = 98.4
For lower limit:
u = x - Zα/2 × (s/√n)
u = 98.2 - 2.58 ( 0.64/√108)
u = 98.2 - 2.58 ( 0.0616)
u = 98.2 - 0.1589
u = 98.04.
The 99% confidence interval for mean temperature of human is :
( 98.04f, 98.40f )
Learn more about Confidence interval at:
https://brainly.com/question/24131141
#SPJ1
Please help with this question.

Answers
The average donut weighs approximately 50 g, and has approximately
11,000 mg of sugar. How much sugar is in three donuts? Answer in g.
Answers
Answer:
33 g
Step-by-step explanation:
the weight of the donut is a distractor number. if each donut has 11,000 mg of sugar, then 11,000 x 3 = 33,000 mg. In order to convert mg into g, we move the decimal over to the left 3 times.
33000. (0 times)
3300.0 (1 time)
330.00 (2 times)
33.000 (3 times)
If you have a statistical calculator or computer, use it to find the actual sample mean and sample standard deviation. Otherwise, use the values Σx = 2769 and Σx2 = 132,179 to compute the sample mean and sample standard deviation. (Round s to four decimal places.)
Answers
By using a statistical calculator, the actual sample mean and sample standard deviation are:
Actual sample mean = 46.1500.
Actual ample standard deviation = 8.6256.
How to calculate the sample mean for the set of data?In Mathematics and Geometry, the sample mean for any set of data can be calculated by using the following formula:
Mean = ∑x/(n - 1)
∑x represents the sum of all data values.(n - 1) represents the number of data contained in a sample.In Mathematics and Geometry, the sample standard deviation for any set of data can be calculated by using the following formula:
Standard deviation, δx = √(1/N × ∑(x - \(\bar{x}\))²)
x represents the observed values of a sample.\(\bar{x}\) is the mean value of the observations.N represents the total number of of observations.By using a statistical calculator, the actual sample mean and sample standard deviation are as follows;
Actual sample mean = 46.1500.
Actual ample standard deviation = 8.6256.
Read more on standard deviation here: brainly.com/question/14467769
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.


Carla had $ 5.50 more than Rhonda. Rhonda had $ 5.00. How much does Carla have in total? A $10.00 B $10.50 C $9.50 D $5.50
Answers
Answer:
10.50
Step-by-step explanation:
5+5.5=10.5............
Answer:
The answer is B $10.50 :)
SOLVE THE SYSTEM ALGEBRAICALLY

Answers
Answer: (4,3) and (-1,8)
Step-by-step explanation:
Before I solve the system, I am going to rewrite it to make it easier for me to understand it.
\(y=x^2-4x+3\\y=-x+7\)
Notice that f(x) and g(x) have been changed into y. The reason is because f(x) and g(x) are the same and stand for y, but we only use f and g to distinguish between the 2 equations. We can use equal values to solve.
\(x^2-4x+3=-x+7\) [add both sides by x]
\(x^2-3x+3=7\) [subtract both sides by 7]
\(x^2-3x-4=0\) [factor]
\((x-4)(x+1)=0\)
Notice that x-4=0 and x+1=0. This means the solutions are x=4 and x=-1.
To find the actual full solution, we have to plug those points back into the original equations.
\(-(4)+7=-4+7=3\\-(-1)+7=1+7=8\)
Therefore, the solutions to this system are (4,3) and (-1,8).
The equation |2x – 12|= 10 has two solutions.
The sum of those two solutions is
Answers
Answer:
-5 and +5
Step-by-step explanation:
add twelve to both sides
New equations: 2x= -+10
Divide by 2 on both sides
x=-5, +5
Answer:
x=11
Step-by-step explanation:
when we add 10 and 12 we get 22 and when we divide
22 by 2 we get 11
How many solutions are to the equation below
9(x-4)= 9x-33
Answers
Answer:
No solution
Step-by-step explanation:
9(x-4)=9x-33
9x-36=9x-33
-9x -9x
36=33
36 is not equal to 33 so therfore
there is no solution
2,239 ÷ 7
Division compatible numbers
Answers
Answer:the answer is 319.857 and round to 320
Step-by-step explanation:
Left F(x) be the number, in thousands, of vehicles a manufacturer estimates will be sold when x million dollars are spent on advertising. If f(1.8)=240, and f(2.5)=325, compute the average rate of change for 1.8 < x< 2.5
Answers
The average rate of change for 1.8 < x < 2.5 is given as follows:
121.43.
How to obtain the average rate of change?The average rate of change of a function is given by the change in the output divided by the change in the input.
The change in the output for this problem is given as follows:
325 - 240 = 85.
The change in the input for this problem is given as follows:
2.5 - 1.8 = 0.7.
Hence the average rate of change is given as follows:
85/0.7 = 121.43.
More can be learned about the average rate of change of a function at brainly.com/question/11627203
#SPJ1
I need help with the second part

Answers
The probability that each bill is a $1 bill is given as follows:
1/16.
How to calculate a probability?A probability is calculated as the division of the desired number of outcomes by the total number of outcomes.
The bills are replaced, hence we consider that for each trial, there is a 1/4 probability of selecting a $1 bill, as one out of the four bills are of $1.
Hence the probability that each bill is a $1 bill is obtained as follows:
p = 1/4 x 1/4
p = 1/16.
More can be learned about probability at https://brainly.com/question/24756209
#SPJ1
What is the slope of the equation y-3 = -4(X - 5)?
04
0-3
20
023

Answers
M=-4 M=-4 M=-4 M=-4 M=-4 M=-4 M=-4
y -3 = -4(x - 5)
y- 3 = -4x -5*(-4)
y - 3 = -4x + 20
y = -4x + 20 + 3
y = -4x + 23
On comparing with the y=mx+b,
Slope = m = -4
Which of the following statements is (are) true about the sampling distribution of the sample mean?
-
The sampling distribution of sample mean will be exactly normally distributed as long as the sample size is at least 30.
-
If the distribution of the sample mean of samples of size 6 looks skewed to the right then the underlying population distribution can't be normal.
-
As n increases, the expected value of the sample mean increases.
-
As n increases, the standard error of the sample mean decreases.
-
The sampling distribution of the sample mean has a mean equal to the population mean μ even if the sample size n is small.
A.
False
B.
True
Answers
Answer:
B.
True
Step-by-step explanation:
next time change it to is/are replace of is(are) (~_~;)
A pizza chef begins to spin a constant volume of dough to make a pie by spinning and tossing the dough into the air, such that the dough takes on a cylindrical shape. The dough's radius increases while the height decreases, but the dough remains a cylinder. At time t = tı, the height of the dough is 1/2 inch, the radius of the dough is 16 inches, and the radius of the dough is increasing at a rate of 2 inches per minute.
Required:
a. At time tı, at what rate is the area of the "top" of the pizza (the part with the toppings) increasing with respect to time? Show the computations that lead to your answer, and indicate units of measure.
b. At time tı, at what rate is the height of the dough decreasing with respect to time?
Answers
Answer:
a ) dAt/dt = 50,24 in/min
dh/dt = - 0,125 in/min
Step-by-step explanation:
The area of the top is At :
At = π*r²
a) Tacking derivatives with respect to time:
dAt/dt = 2* π*r * dr/dt
At t = t₁ r = 16 in and dr/dt = 0,5
Then
dAt/dt = 2*3,14*16*0,5 in/min
a ) dAt/dt = 50,24 in/min
b) The volume of the cylinder is:
Vc = π*r²*h ( where h is the heigh of the cylinder )
Tacking derivatives with respect to time
dVc/dt = 2* π*r*h*dr/dt + π*r²*dh/dt
But dVc/dt = 0 since the volume remains constant, then:
π*r²*dh/dt = - 2* π*r*h*dr/dt
r*dh/dt = - 2*h*dr/dt
dh/dt = - 2*0,5*2/16 in/min
dh/dt = - 0,125 in/min
A projectile is launched from the ground with an initial speed of 220 ft/sec at an angle of 60° with the horizontal.
What is the height of the projectile after 4 seconds?
How long is the projectile in the air?
What is the horizontal distance traveled by the projectile?
What is the maximum height of the projectile?
Answers
The height of the projectile after 4 seconds is 421.28 ft.
The projectile is in the air for 8.015 seconds.
The horizontal distance traveled by the projectile is 881.77 ft.
The maximum height of the projectile is 464.1 ft.
To solve this problem, we can use the kinematic equations of motion for a projectile.
Let's assume that the initial height of the projectile is zero.
What is the height of the projectile after 4 seconds:
We can use the equation:
\(y = yo + vot + 1/2at^2\)
where
y = height of the projectile
yo = initial height (zero in this case)
vo = initial vertical velocity = 220 sin(60°) = 190.53 ft/sec
a = acceleration due to gravity \(= -32.2 ft/sec^2\) ( negative since it acts downwards)
t = time = 4 sec
Plugging in the values, we get:
\(y = 0 + (190.53)(4) + 1/2(-32.2)(4)^2 = 421.28 ft\)
Therefore, the height of the projectile after 4 seconds is 421.28 ft.
Long is the projectile in the air:
The time of flight of a projectile can be calculated using the equation:
t = 2vo sinθ / g
where θ is the launch angle and g is the acceleration due to gravity.
Plugging in the values, we get:
t = 2(220 sin(60°)) / 32.2 = 8.015 sec
Therefore, the projectile is in the air for 8.015 seconds.
Horizontal distance traveled by the projectile:
The horizontal distance traveled by the projectile can be calculated using the equation:
\(x = xo + vot + 1/2at^2\)
where
x = horizontal distance traveled
xo = initial horizontal position (zero in this case)
vo = initial horizontal velocity = 220 cos(60°) = 110 ft/sec
a = acceleration due to gravity (zero in the horizontal direction)
t = time = 8.015 sec
Plugging in the values, we get:
\(x = 0 + (110)(8.015) + 1/2(0)(8.015)^2 = 881.77 ft\)
Therefore, the horizontal distance traveled by the projectile is 881.77 ft.
Maximum height of the projectile:
The maximum height of a projectile can be calculated using the equation:
\(ymax = yo + (vo^2 sin^2 \theta ) / 2g\)
Plugging in the values, we get:\(ymax = 0 + (190.53^2 sin^2(60\degree )) / (2)(32.2) = 464.1 ft\)
Therefore, the maximum height of the projectile is 464.1 ft.
For similar question on projectile.
https://brainly.com/question/30695754
#SPJ11
Apply the properties and simplify -479 + 3.7 + 479( please help )
Answers
Given:
\(-479+3.7+479\)Required:
Simplify the expression.
Explanation:
The given expression is:
\(-479+3.7+479\)Simplify the expression as:
\(3.7+(-479+479)\)Apply the addition property.
\(\begin{gathered} =3.7+0 \\ =3.7 \end{gathered}\)Final answer:
The simplification of the expression is 3.7
What the meaning of "Define F(x) = α if α is isomorphic to the initial segment of W given by x"?

Answers
The given statement defines a function F(x) that associates a unique ordinal number α to each initial segment of a well-ordered set W. The function F(x) assigns the ordinal α to the initial segment of W determined by x if and only if α is isomorphic (structurally equivalent) to that initial segment.
To prove the uniqueness of the ordinal number associated with each initial segment, we rely on Lemma 2.7 (presumably mentioned earlier). This lemma likely establishes some properties of isomorphic well-ordered sets, such as uniqueness of isomorphisms or a specific correspondence between ordinals and well-ordered sets.
Using the Replacement Axioms, we can show that the set F(W) exists, as it is obtained by applying the function F to each element of W and collecting the results as a set.
For each initial segment of W, there exists an ordinal α that is isomorphic to that segment; otherwise, we can consider the least element r for which no such ordinal exists. By definition, F(r) does not have a well-defined value, contradicting the construction of F.
Finally, if y is the least element in the set F(W), then F(W) = y, and we have established an isomorphism between W and the ordinal y.
In summary, the proof demonstrates that for any well-ordered set W, there exists a unique ordinal number (denoted by F(W)) that is isomorphic to W, confirming the statement that every well-ordered set is isomorphic to a unique ordinal number.
For more such questions on ordinal number
https://brainly.com/question/30954769
#SPJ8
Find the measures of angles x,y and z in the figure
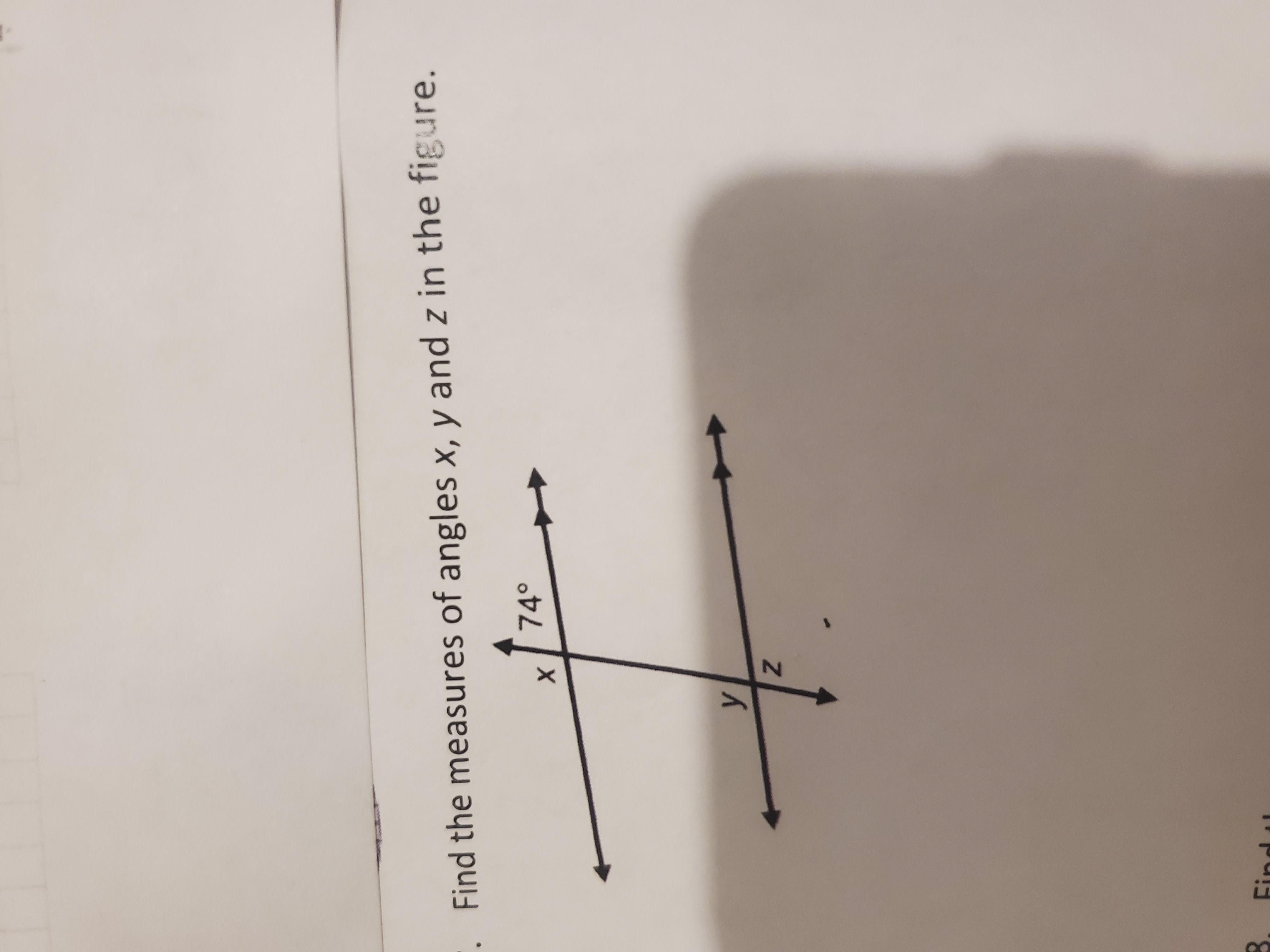
Answers
The value of x, y and z in the diagram are:
x = 106°y = 106°z = 106°How do i determine the value of x, y and z?1. The value of x in the diagram can be obtained as illustrated below:
x + 74 = 180° (angle on a straight line)
Collect like terms
x = 180 - 74
x = 106°
Thus, from the above calculation, we can conclude that the value of x is 106°
2. The value of y can be obtained as follow:
Value of x = 106°Value of y =?From the diagram,
m∠x = m∠y (Corresponding angles)
106° = m∠y
Value of y = 106°
3. The value of z can be obtained as follow:
Value of y = 106°Value of z =?From the diagram,
m∠y = m∠z (vertically opposite angles)
106° = m∠z
Value of z = 106°
Learn more about transversal and Parallel Lines:
https://brainly.com/question/25903313
#SPJ1
Which number is greater in the following inequality: x > 5 ? *
Answers
Answer:
.
Step-by-step explanation:
Answer: I believe it is 5
Step-by-step explanation: Because that's what the symbol is showing
Suppose you have a treatment that you suspect may alter performance on a certain task. You compare the mean of your sample to the norm. Further, suppose you use az-test for means and your result is statistically significant (z=2.70,p<0.05, one-taifed). Glven your statistically significant result, indicate which (if anyl of the following statements is true. Check each statement that is true. In other words, you may check none, one, several, or all of the statements. You have absoluidy disproved the null hypothesis ghat is, there is no ditference between the population means). You have found the protablity of the null hypothesis being true.
Answers
All of the assertions are false. A statistically significant finding does not necessarily imply that the null hypothesis has been proven incorrect, nor does it indicate how likely it is to be true.
What is a norm defined as?Generally speaking, the word "norm" describes something that is customary, typical, anticipated, or standard. Norms are established definitions of beneficial attitudes and actions that ought to be commonplace, or "the norm," whenever a group is working together. They apply to cooperation and collaboration.
What Is a Z-Test?When the variances are known and the sample size is large, a z-test is a statistical test that is used to assess whether two population means differ from one another.
to learn more about null hypothesis visit link:
https://brainly.com/question/16945299
4. Verify the following for a = 3 and b = 4.
a) (a + b)^2= a^2 + 2ab + b^2
b)(a + b)^2 = a^2 - 2ab + b^2
c) (a + b)(a - b) = a^2 - b^2
Answers
Answer:
(3+4)^2=9+24+16
7^2
=49
Ricardo ran four miles in 31 minutes. It took him 6.25 minutes to run the first mile. Ricardo ran the remaining miles at a slow and steady speed. How long did it take him to run each of the last three miles?
Answers
Answer:
8.25 minutes
Step-by-step explanation:
31 minutes-6.25 minutes=24.75 remaining miutes between the last 3 miles so then you take 24.75 minutes÷ 3 miles remaining= 8.25 minutes each last 3 miles
a gardener is growing tomato plants. one plant starts out 5 cm tall. it grows a constant 2 cm every week. what equation represents the height h of the plant after t weeks
a t= 5h+2
b t= 2h+5
c h=5t + 2
d h = 2t+5
Answers
Answer:
D) h=2t+5
Step-by-step explanation:
Caroline buys a plant from the store that is 12 cm tall.
Every week, the plant grows 2 cm.
Let heheight of the plant and w=weeks.
Click "show your work" and complete all of the tasks in
the whiteboard
Answers
Answer:
Height in w week = 12 + 2w
Step-by-step explanation:
Given:
Height of plant = 12 cm
Rate of plant growth = 2 cm per week
Find:
Equation
Computation:
Height in w week = Height of plant + (Rate of plant growth)(Number of week)
Height in w week = 12 + (2)(w)
Height in w week = 12 + 2w
EXTRA POINTS
If the Green family deposits $2,500 in a savings account that earns
2.75% interest compounded continuously, approximately how long until
the Green family will have doubled their initial investment?
Use: y= perE
-25 vears
-16 years
-19 years
-22 years
Answers
The green family will double their investment in 34 years after the principal is subject to compound interest continuously.
The principal invested = $2500
Rate of interest annually = 2.75%
Time = t years
Amount = double of principal = 2500 × 2 = $ 5000
Interest is compounded continuously
Formula to calculate the amount is given by:
\(A=Pe^{rt}\)
Now we will use the values to find the exact value of t
or, \(5000 = 2500 e^{0.0275t}\)
or, ln 2 = 0.0275t
or, t = 25.205 years
or, t ≈ 25 years
Compound interest allows interest to accumulate over time as opposed to simple interest, which does not compound because prior interest is simply not added to the principal for the current period.
The simple annual interest rate is obtained by multiplying the interest per period by the total number of periods in a year.
Hence the Green family will have doubled the investment in approximately 25 years.
To learn more about compound interest visit:
https://brainly.com/question/13155407
#SPJ1
what is another ratio that is equivalant to 5:3 and 10:6?
Answers
Answer:
5:3 = 10:6
10:6 = 20:12 or 5:3