a machinist is making a gear that will pull a chain at 60 ft/min when rotating at 40 rev/min. What should the radius of the gear be? Answer in inches.
Answers
The radius of the gear should be approximately 2.8644 inches.It is important to note that when making calculations involving units, we need to make sure that all units are consistent and convert them when necessary. In this case, we converted the answer from feet to inches to match the given unit.
To find the radius of the gear that will pull a chain at 60 ft/min when rotating at 40 rev/min, we can use the formula:
chain speed = 2 x pi x radius x rotational speed
where pi is a mathematical constant approximately equal to 3.14.
We know that the chain speed is 60 ft/min and the rotational speed is 40 rev/min, so we can substitute those values into the formula:
60 = 2 x 3.14 x radius x 40
Simplifying the equation, we get:
radius = 60 / (2 x 3.14 x 40)
radius = 0.2387 ft
To convert feet to inches, we can multiply the answer by 12:
radius = 0.2387 x 12 = 2.8644 inches.
For such more questions on Radius:
https://brainly.com/question/24375372
#SPJ11
Related Questions
Find the unit rate (constant of proportionality) of the distance traveled.
Number of hours
0.25 1.5 2.5 3
Distance traveled (km) 3 18 30 36
Answers
Answer:
12.
Step-by-step explanation:
if to re-write the given condition, then
\(\frac{3}{0.25} =\frac{18}{1.5} =\frac{30}{2.5} =\frac{36}{3} ;\)
it is clear, the required constant is 12 (12 per hour).
Task 3 add
3/4+1/4
2/3+1/3
5/6+2/6
7/8+1/8
4/5+3/5
Answers
The answer for the given questions are:
1. 3/4 + 1/4 = 1
2. 2/3 + 1/3 = 1
3. 5/6 + 2/6 = 7/6
4. 7/8 + 1/8 = 1
5. 4/5 + 3/5 = 1 2/5
To solve the addition problems involving fractions, let's approach each one step by step:
1. 3/4 + 1/4:
When adding fractions with the same denominator, you simply add the numerators while keeping the denominator the same. In this case, since both fractions have a denominator of 4, you can add the numerators, which gives us 3 + 1 = 4. Therefore, the sum is 4/4. However, 4/4 is equivalent to the whole number 1. So, the answer to 3/4 + 1/4 is 1.
2. 2/3 + 1/3:
Similar to the previous problem, these fractions have the same denominator, which is 3. Adding the numerators, we have 2 + 1 = 3. Therefore, the sum is 3/3, which simplifies to 1. So, 2/3 + 1/3 equals 1.
3. 5/6 + 2/6:
Again, the denominators are the same, so we can add the numerators: 5 + 2 = 7. The sum is 7/6. However, 7/6 cannot be simplified any further, so that is the final answer.
4. 7/8 + 1/8:
Both fractions have a denominator of 8. Adding the numerators, we get 7 + 1 = 8. Therefore, the sum is 8/8. Similar to the first example, 8/8 is equivalent to the whole number 1. So, 7/8 + 1/8 equals 1.
5. 4/5 + 3/5:
These fractions share a denominator of 5. Adding the numerators, we have 4 + 3 = 7. Hence, the sum is 7/5. However, 7/5 can be simplified as a mixed number, which is 1 2/5. Therefore, 4/5 + 3/5 equals 1 2/5.
In summary, the solutions to the addition problems are as follows:
1. 3/4 + 1/4 = 1
2. 2/3 + 1/3 = 1
3. 5/6 + 2/6 = 7/6
4. 7/8 + 1/8 = 1
5. 4/5 + 3/5 = 1 2/5
For more questions on fractions, click on:
https://brainly.com/question/30340082
#SPJ8
Drag each tile to its equivalent measure, rounded to the nearest tenth.
Options: 19.8, 10.2, 22.7, 15.4
Measure Equivalent
4 in. _____ Cm
7 kg _____lb
6 gal _____L
65 ft _____ m
Answers
The correct matches are: 4 in. → 10.2 cm , 7 kg → 15.4 lb
6 gal → 22.7 L and 65 ft → 19.8 m.
What are conversions?Conversions refer to the process of changing a measurement from one unit to another unit that measures the same quantity.
For example, converting distance from miles to kilometers, or converting weight from pounds to kilograms.
Here are the conversions:
1 inch = 2.54 cm (approx.)
1 kg = 2.205 lb (approx.)
1 gal = 3.785 L (approx.)
1 ft = 0.3048 m (approx.)
Using these conversions, we can find the equivalent measures:
4 in. → 4 × 2.54 = 10.16 ≈ 10.2 cm
7 kg → 7 × 2.205 = 15.435 ≈ 15.4 lb
6 gal → 6 × 3.785 = 22.71 ≈ 22.7 L
65 ft → 65 × 0.3048 = 19.812 ≈ 19.8 m
To know more about equivalent measures visit:
https://brainly.com/question/29156458
#SPJ1
12) What type of triangles will always be similar to one another?
Answers
Answer:
Right
Step-by-step explanation:
Answer: Two equilateral triangles are always similar.
Step-by-step explanation:
If there are 5 levels of Factor A and 7 levels of Factor B for an ANOVA with interaction, what are the interaction degrees of freedom?
a. 24.
b. 12.
c. 10.
d. 35.
Answers
Answer:
C. 10Step-by-step explanation:
let n1 be the degree of freedom of factor A
Let n2 be the degree of freedom of factor B
If there are 5 levels of factor A, then n1 = 5
If there are 7 levels of Factor B then n2 = 7
The interaction between the degrees of freedom is expressed using the formula;
df = (n1 - 1)+(n2 - 1)
df = n1 -1 + n2- 1
df = n1+n2 -2
Substitute n1 and n2 and get df
df = 5+7-2
df = 12-2
df = 10
Hence the interaction degree of freedom is 10
PLEASEEEE HELP!!!! (Multiplying/Dividing Fractions Word Problems) An auto shop installed a new automatic system to do paint jobs for cars. The system can paint 6 cars in an hour. How long does it take to paint one car?
Answers
Answer:
10 minutes.
Step-by-step explanation:
Note the amount of minutes in an hour.
1 hour = 60 minutes.
The system can paint 6 cars in an hour. Divide 60 minutes with 6 cars:
60/6 = 10
Each car takes 10 minutes to get fully painted.
~
what the answer please

Answers
Using the law of detachment and the law of syllogism,
We can conclude that Sally is too heavy for the bridge, but we cannot conclude that she can cross the bridge.
We have,
Using the law of detachment, we can conclude from statements 1 and statement 3:
If something weighs more than 2,000 pounds, then it weighs more than Jill's car. (Statement 1)
Sally the elephant weighs 2,325 pounds. (Statement 3)
Therefore, Sally weighs more than Jill's car.
Using the law of syllogism, we can then use the conclusion above and statement 2 to conclude:
Sally weighs more than Jill's car.
If something weighs more than Jill's car, then it is too heavy for the bridge. (Statement 2)
Therefore, Sally is too heavy for the bridge.
Therefore,
We can conclude that Sally is too heavy for the bridge, but we cannot conclude that she can cross the bridge.
Learn more about the law of detachment here:
https://brainly.com/question/29251767
#SPJ1
Evaluate the expression
12 - 3 2+429,- 4) for y = 3.

Answers
Answer:
9,427) y=5
is correct answer
the point halfway between two endpoints of a line segment
Answers
The midpoint of a line segment is the point that is halfway between the two ends of the line segment. A midway separates a line segment into two equal parts.
This is further explained below.
What is a line segment?Generally, In the field of geometry, a line segment is defined as the portion of a line that is enclosed by two unique points on the line.
Alternatively, we may say that a line segment is the portion of a line that is between two points. A line does not have any endpoints and may stretch endlessly in any direction, however, a line segment has two endpoints that are fixed or definite in some way.
In conclusion, The term "midpoint" refers to the point along a line segment that is situated exactly midway between the beginning and ending points. A midway separates a line segment into two equal parts.
Read more about the line segment
https://brainly.com/question/25727583
#SPJ1
Which property of addition is shown in the equation below?
a + bi + 0 + Oi = a + bi
A.commutative property
B.inverse property
C.identity property
D.associative property
Answers
Answer:
This is the identity property. It means that any number added by zero would be the same number. In the second expression the zeroes were taken away.
Step-by-step explanation:
like and 5 start luv u
Solve the system: xy=4 x^2+y^2=8
Answers
Answer:
Step-by-step explanation:
\(xy=4\\x^{2} +y^{2} =8\)
We isolate x and then replace it in the other equation
\(x=\frac{4}{y}\)
\((\frac{4}{y})^{2} +y^{2}=8\) --> \(\frac{16}{y^{2}} + y^{2} =8\)
In the end, you have
\(\frac{16}{y^{2} } +\frac{y^{4} }{y^{2}}=\frac{8y^{2} }{y^{2} } \\\)
You now multiply y² in both sides so that in the end there is
\(16+y^{4}=8y^{2}\)
Next step:
\(y^{4}-8y^{2}+16=0\)
\(y^{2} =a\)
You substitute a in the equation
\(a^{2} -8a+16=0\)
Now, as you can see
\(a^{2} -8a+16=(a-4)^{2}\)
The result is that \(a=4\)
Therefore,
\(y=2\\y=-2\)
In the \(x=\frac{4}{y}\) equation you substitute both values of y
\(x=\frac{4}{2} =2\\x=-\frac{4}{2} =-2\)
What is the sum of the squares of the first 100 integers?
Answers
0
.
The numbers from
1
to
100
are in A.P.
The formula for the sum of the first
n
natural number is
n
n
+
1
2
.
The number of natural numbers for the given series is
100
.
The sum of first
100
natural numbers is
100
100
+
1
2
=
50
×
101
=
5050
Hence the sum of first
100
natural numbers is
5050
.
I am lost please help thank you all

Answers
Answer:
Step-by-step explanation:
At least 9 means more than 9 and includes 9
x ≥ 9 and [9, +∞)
At most 9 means numbers less than 9
x≤9 and (-∞, 9]
more than 9 means bigger than 9 but not including 9
x > 9 and (9, +∞)
fewer than 9 means less than 9 but not including 9
x<9 and (-∞, 9)
strictly between 7 and 9 means between 7 and 9 but not including
7<x<9 and (7,9) (This is the only one I'm unsure of. Strictly, not sure if it includes or doesn't include, usually it just says include or doesn't include)
between 7 and 7 inclusive. means it's just =7 There's no boundaries
x=7
no more than 7 means less than 7 and includes 7
x ≤ 7 and (-∞, 7]
lesson 5.4
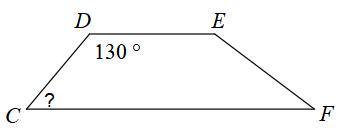
1 .Find the measurement of the angle indicated for each trapezoid.
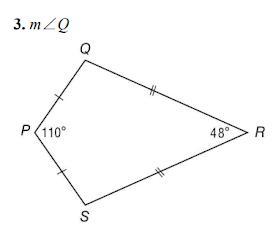
2.Find the measure.
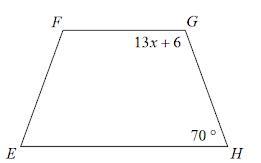
3.Solve for [x]. Each figure is a trapezoid.
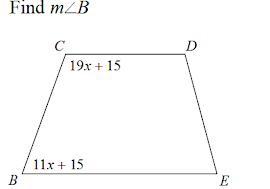
4.Find the measurement of the angle indicated for each trapezoid.
Answers
Question 1
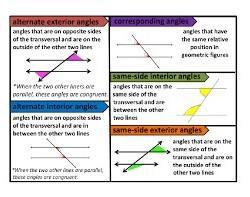
Opposite sides of a trapezoid are parallel. So, by the same-side interior angles theorem,
\(m\angle C+130^{\circ}=180^{\circ} \\ \\ m\angle C=50^{\circ}
\)
Question 2
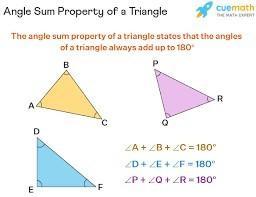
Drawing PR, we form congruent triangles PQR and PSR. Thus, using the sum of angles in a triangle,
\(55^{\circ}+24^{\circ}+m\angle Q=180^{\circ} \\ \\ m\angle Q=101^{\circ}\)
Question 3
Opposite sides of a trapezoid are parallel. So, by the same-side interior angles theorem,
\(13x+6+70=180 \\ \\ 13x+76=180 \\ \\ 13x=104 \\ \\ x=8\)
Question 4
Opposite sides of a trapezoid are parallel. So, by the same-side interior angles theorem,
\(11x+15+19x+15=180 \\ \\ 30x+30=180 \\ \\ 30x=150 \\ \\ x=5 \\ \\ m\angle B=11(5)+15=70^{\circ}\)
Sally is given $850. Every year, she decides to donate 9% of this money to charity until she has none left.
After 34 years, approximately how much money will Sally have left?
Answers
Answer:
Step-by-step explanation:
Year 1: $850 * 0.91 = $773.50
Year 2: $773.50 * 0.91 = $704.69
Year 3: $704.69 * 0.91 = $641.95
...
Year 34: (continue the pattern)
We can continue this calculation for each year, but to save time, we can use an exponential decay formula:
Remaining Amount = Initial Amount * (1 - rate)^years
Substituting the values:
Remaining Amount = $850 * (1 - 0.09)^34
Calculating this expression:
Remaining Amount ≈ $850 * (0.91)^34 ≈ $255.88
After 34 years, approximately $255.88 will be left with Sally.
What is the value of x? Round to the nearest thousandth.

Answers
Applying the tangent ratio, the value of x in the image, rounded to the nearest thousandth is: 15.824.
How to Find the Value of x Using the Tangent Ratio?The tangent ratio, commonly referred to as "tangent," is a trigonometric function that relates the ratio of the length of the side opposite an angle to the length of the side adjacent to that angle in a right triangle. It is expressed as:
tan (∅) = opposite/adjacent
We have the following:
Reference angle (∅) = 53 degrees
Length of opposite side = 21
Length of adjacent side = x
Plug in the values:
tan 53 = 21/x
x * tan 53 = 21
x = 21 / tan 53
x = 15.824
Learn more about Tangent Ratio on:
question
#SPJ1
Which of the following shows 4x+23+7x-12+y in simplest terms
Answers
Answer:
11x+25+y
Step-by-step explanation:
If you simplify, you get...
(4+7)x+(23+12)+y
11x+25+y
Hope I helped!
If f(x) = x2 – 25 and g(x) = x – 5, what is the domain of (StartFraction f Over g EndFraction) (x)?
Answers
Answer:
x≠5
or
\(\:\left(-\infty \:,\:5\right)\cup \left(5,\:\infty \:\right)\)
Step-by-step explanation:
Both the answers above are correct, but the second is written in interval notation; there are also other ways to represent this same domain. The domain of a function are the possible x-values.
To find the domain, you must first find the new function. We are looking for \(\frac{f}{g} (x)\). This means you need to divide f(x)'s rule by g(x)'s rule. This equals \(\frac{f}{g}(x)=\frac{x^{2} -25}{x-5}\). To find the domain, remember that functions are undefined when the denominator is 0. So, x cannot equal 5 because this would make the denominator 0.
Suppose 3 and 8 are the only individual scores that can be made in a certain game. How many integer total scores are impossible to obtain?
Answers
Answer: 3
Step-by-step explanation:
3x8 = 24
24x2= 48!
8x12= 96!
Answers must be divisible by both numbers, and achievable by both inputs.
Hope This Helped
A number is a rational number if and only if it can be represented as a terminating decimal.
p: A number is a rational number.
q: A number can be represented as a terminating decimal.
Which represents the converse of this statement? Is the converse true?
The converse of the statement is true.
The converse of the statement is false.
The converse of the statement is sometimes true and sometimes false.
Answers
The converse of the statement "A number is a rational number if and only if it can be represented as a terminating decimal" would be "A number can be represented as a terminating decimal if and only if it is a rational number."
To determine the truth value of the converse, we need to analyze its validity. The converse statement suggests that all numbers that can be represented as terminating decimals are rational numbers, and all rational numbers can be represented as terminating decimals.
However, this converse statement is false. While all rational numbers can be represented as terminating decimals or repeating decimals, not all terminating decimals are rational numbers.
There are numbers, such as irrational numbers like pi (π) or the square root of 2 (√2), that cannot be expressed as terminating decimals but are still real numbers.
Therefore, the correct answer is: The converse of the statement is false.
For more details regarding converse statement, visit:
https://brainly.com/question/31918837
#SPJ1
What is the equation of the line shown in this graph?
у
5
4
3
(-2,2)
2
1
-5
-4
-3 -2
-1 0
1
2.
3
4
5
-1
-27
(-2,-3)
-3
-4
Answers
Answer: (1,-4)
Step-by-step explanation:ssghvssd5633
which of the following functions grows fastest? group of answer choices n log n n log n n / log n n - log n n log n
Answers
In the following option n log n seems to grow the fastest amongst all according to the size of inputs.
In computer science and mathematics, the running time or complexity of an algorithm is often measured in terms of the size of the input, usually denoted by n. The notation O(f(n)) is used to describe the upper bound on the running time of an algorithm, where f(n) is a function of n.
In the context of comparing growth rates of functions, we usually only consider the highest-degree term of the function. For example, we would say that f(n) = n^2 + n grows as O(n^2), because n^2 grows much faster than n and dominates the running time as n grows larger.
Now, let's consider the functions n, n / log n, n - log n, n log n, and n^2. As n grows, each of these functions grows at a different rate.
1. n grows linearly with n, so it takes more time as the size of the input grows.
2. n / log n grows faster than n, but slower than n log n. This is because logarithms grow much slower than linear functions, but as n grows larger, the difference between n and log n becomes larger, so n / log n grows faster.
3. n - log n grows slower than n and n / log n, because log n grows much slower than n, so as n grows larger, n - log n becomes closer to n.
4. n log n grows faster than n, n / log n, and n - log n, but slower than n^2. This is because logarithms grow much slower than linear functions, but as n grows larger, the difference between n and log n becomes larger, so n log n grows faster.
5.n^2 grows much faster than n, n / log n, n - log n, and n log n, so as n grows larger, n^2 becomes much larger than any of these functions.
So, of the options given, n log n grows the fastest, meaning that an algorithm that takes time proportional to n log n will become slower faster as the size of the input grows than an algorithm that takes time proportional to n, n / log n, or n - log n.
To learn more about algorithms click here:
brainly.com/question/27522570
#SPJ4
An Olympic swimming pool is 50 m long, 25 m wide, and 1.5 m deep. How many Olympic pools would be filled by the dollar bills spent by the U.S. federal government in 2011
Answers
Answer:
Number of dollars bills that can be fitted in Olympic pool = 1.67 billion.
Step-by-step explanation:
The dimensions of a dollar bill are 15.5956 cm by 6.6294 cm by 0.010922 cm. The U.S. federal government spent $3.8 trillion in fiscal year 2011.
An Olympic swimming pool is 50 m long, 25 m wide, and 1.5 m deep. How many Olympic pools would be filled by the dollar bills spent by the U.S. federal government in 2011
From above,
The volume for the dimension of the dollar bill = 15.5956 cm × 6.6294 cm × 0.010922 cm
The volume for the dimension of the dollar bill = 1.12922 cm³
The volume for the dimension of the dollar bill = 1.12922 × 10⁻⁶ m³
The volume of the pool = 50 m × 25 m × 1.5 m
The volume of the pool = 1875 m³
Number of dollars bills that can be fitted in pool = volume of the pool/volume of the dimension of dollar bills
Number of dollars bills that can be fitted in Olympic pool =1875 m³ / 1.12922 × 10⁻⁶ m³
Number of dollars bills that can be fitted in Olympic pool = 1,660,438,180
Number of dollars bills that can be fitted in Olympic pool = 1.67 billion.
A friend of mine is giving a dinner party. His current wine supply includes bottles of zinfandel, of merlot, and of cabernet (he only drinks red wine), all from different wineries. If he wants to serve bottles of zinfandel and serving order is important, how many ways are there to do this? If bottles of wine are to be randomly selected from the for serving, how many ways are there to do this? If bottles are randomly selected, how many ways are there to obtain two bottles of each variety? If bottles are randomly selected, what is the probability that this results in two bottles of each variety being chosen? If bottles are randomly selected, what is the probability that all of them are the same variety?
Answers
Answer:
Explained below.
Step-by-step explanation:
The complete question is:
A friend of mine is giving a dinner party. His current wine supply includes 8 bottles of zinfandel, 10 of merlot, and 12 of cabernet (he only drinks red wine), all from different wineries. a. If he wants to serve 3 bottles of zinfandel and serving order is important, how many ways are there to do this? b. If 6 bottles of wine are to be randomly selected from the 30 for serving, how many ways are there to do this? c. If 6 bottles are randomly selected, how many ways are there to obtain two bottles of each variety? d. If 6 bottles are randomly selected, what is the probability that this results in two bottles of each variety being chosen? e. If 6 bottles are randomly selected, what is the probability that all of them are the same variety?
Solution:
In mathematics, the procedure to select k items from n distinct items, without replacement, is known as combinations.
The formula to compute the combinations of k items from n is given by the formula:
\({n\choose k}=\frac{n!}{k!(n-k)!}\)
Permutation is the number of ways to select k items from n distinct items in a specific order.
The formula to compute the permutation or arrangement of k items is:
\(^{n}P_{k}=\frac{n!}{(n-k)!}\)
(a)
The number of ways to serve 3 bottles of zinfandel, with a specific order is:
\(^{8}P_{3}=\frac{8!}{(8-3)!}=\frac{8\times7\times6\times5!}{5!}=336\)
(b)
The number of ways to select 6 bottles from the 30 is:
\({30\choose 6}=\frac{30!}{6!(30-6)!}=\frac{30!}{6!\times 24!}=593775\)
(c)
The number of ways to select two bottles of each variety is:
\({8\choose 2}\times {10\choose 2}\times {12\choose 2}=\frac{8!}{2!\times6!}\times \frac{10!}{2!\times8!}\times \frac{12!}{2!\times10!}\)
\(=\frac{12!}{(2!)^{3}\times 6!}\\\\=83160\)
(d)
Compute the probability of selecting two bottles of each variety if 6 bottles are selected:
\(P(\text{2 bottles of each})=\frac{83160}{593775}=0.14\)
(e)
Compute the probability of selecting the same variety of bottles, if 6 bottles are selected:
\(P(\text{Same Variety})=\frac{{8\choose 6}+{10\choose 6}+{12\choose 6}}{{30\choose 6}}\)
\(=\frac{28+210+924}{593775}\\\\=0.0019570\\\\\approx 0.002\)
Given vectors = (-6,4) and v=(7, 10), determine if the vectors are orthogonal. If they are not orthogonal, find the angle between the two vectors
Answers
The given vectors are:
\(\begin{gathered} u=\langle-6,4\rangle \\ v=\langle7,10\rangle \end{gathered}\)Two vectors are orthogonal if the dot product of the two vectors is zero, let's check:
\(\begin{gathered} u\cdot v=(-6)*7+(4*10) \\ u\cdot v=-42+40 \\ u\cdot v=-2 \end{gathered}\)As the product is not zero, then they are not orthogonal.
Now, we need to find the angle between them:
\(\cos\theta=\frac{u\cdot v}{||u||*||v||}\)We already know u*v, now, let's find ||u|| and ||v||:
\(\begin{gathered} ||u||=\sqrt{(-6)^2+(4)^2}=\sqrt{36+16}=\sqrt{52} \\ ||v||=\sqrt{7^2+10^2}=\sqrt{49+100}=\sqrt{149} \end{gathered}\)Now, replace these values, and solve for theta:
\(\begin{gathered} \cos\theta=\frac{-2}{\sqrt{52}*\sqrt{149}}=\frac{-2}{\sqrt{7748}}=\frac{-2}{88.02} \\ \cos\theta=-0.023 \\ \theta=\cos^{-1}(-0.023) \\ \theta=91.3\degree \end{gathered}\)The answer is B. The vectors are not orthogonal. The angle between them is 91.3°
Find the value of x and y variable in the following parallelogram

Answers
Answer:
y + 5 = 3y - 1
2y = 6, so y = 3
4x - 2 = x + 10
3x = 12, so x = 4
Do the following sets of data represent a function? Justify your answer.
1. (1,4), (2, 4), (3, 5), (2, 2)
2. (10, 5), (12, 5), (7, 12), (12, 2)
3. (0, 0), (5, 4), (4, 5), (1, 0)
Answers
1. No, the set of data does not represent a function.
A function relates an input to an output. It is like a machine that has an input and an output. And the output is related somehow to the input.
We are given with (1,4), (2, 4), (3, 5), (2, 2)
This is because every output of this data does not have unique input.
4 and 2 have the same input i.e. 2.
2. Yes, the set of the data represents a function.
We are given with (10, 5), (12, 5), (7, 12), (12, 2)
It is a function as every input has a single output.
So, (10, 12, 07) are the elements of the domain and (2, 5, 7, 12) is the range of the function.
3. Yes, it is a function as every input of this data represents the single and unique output.
We are given with (0, 0), (5, 4), (4, 5), (1, 0)
It has its unique elements and domain (0,1,4,5) and range is from (0, 1, 2, 3, 4, 5).
Learn more about functions here :
https://brainly.com/question/14418346
#SPJ9
The EPA is also interested in controlling the local population of deer. This could be done
by expanding or reducing the duration of each year's hunting season. After collecting
decades of data, a team of researchers developed a quadratic model relating the local
deer population to the duration of each year's hunting season.
P = -10h² + 30h + 237
Here P is the population of deer at the end the year while h is the length of that year's
hunting season that year, measured in months. What is the maximum amount of deer this
model predicts? What does the model predict the population of deer would be if the
government allowed year-round? What would this actually mean?
Answers
The model predicts a negative population (-843) if the hunting season lasts the entire year.
To find the maximum amount of deer predicted by the quadratic model, we need to determine the vertex of the quadratic function. The vertex of a quadratic function in the form of \(y = ax^2 + bx + c\) can be found using the formula x = -b / (2a). In this case, the quadratic model is \(P = -10h^2 + 30h + 237.\)
Using the formula, we can calculate the value of h at the vertex:
\(h = -30 / (2\times(-10)) = 1.5\)
Substituting this value back into the equation, we can find the maximum population of deer:
\(P = -10(1.5)^2 + 30(1.5) + 237\\P = -22.5 + 45 + 237\\P = 259.5\)
Therefore, the model predicts that the maximum population of deer would be 259.5 at the end of the year if the hunting season duration is optimized based on the quadratic model.
If the government allowed year-round hunting, we can assume the hunting season duration (h) would be 12 months. Substituting this value into the equation, we can find the predicted population of deer:
\(P = -10(12)^2 + 30(12) + 237\\P = -1440 + 360 + 237\\P = -843\)
However, in practical terms, a negative population is not meaningful. It suggests that the quadratic model might not accurately represent the population dynamics in the case of a year-round hunting season. This could be due to various factors, such as migration patterns, breeding habits, or the influence of other ecological factors not considered in the model.
Further research and data analysis would be needed to develop a more accurate model or understand the population dynamics under different hunting scenarios.
For more such questions on population
https://brainly.com/question/30396931
#SPJ8
Does the expressions
\( \sqrt{100 - 64} \)
and
\( \sqrt{100 - \sqrt{64} } \)
have the same value?
Answers
Answer:
No. they have a difference in value
the first ans is 6 while the second gives 9.56
The mass of a lorry and its load is 2.87t. What is the mass of the load in kg, if the mass of the lorry is 1.225 tonnes?
a) 1.645kg
b) 1645kg
c) 1225kg
d) 0.001645kg
Answers
The mass of the load in kilogram is an illustration of subtraction operation
The mass of the load in kilogram is (b) 1645 kg
The complete mass is given as:
\(\mathbf{m_t = 2.87\ tonnes}\)
The mass of the lorry is given as:
\(\mathbf{m_l = 1.225\ tonnes}\)
The mass of the load is calculated by subtracting the mass of the lorry from the mass of the lorry and its load.
So, we have the following equation:
\(\mathbf{m_{load} = m_t - m_l}\)
Substitute known values
\(\mathbf{m_{load} = 2.87\ tonnes- 1.225\ tonnes}\)
Subtract
\(\mathbf{m_{load} = 1.645\ tonnes}\)
Convert to kilogram
\(\mathbf{m_{load} = 1.645 \times 1000kg}\)
Multiply
\(\mathbf{m_{load} = 1645 kg}\)
Hence, the mass of the load in kilogram is (b) 1645 kg
Read more about subtraction at:
https://brainly.com/question/20671719