a pita ya or dragon fruit is a tropical fruit with pink skin and pulp filled with tiny black seeds the weight of a pitaya is 1x10~3 ounces what is the weight of the pitaya seed in standard form
Answers
Answer:
To convert the weight of the pitaya seed from ounces to standard form, we need to express it in scientific notation.
Given: Weight of the pitaya seed = 1x10^(-3) ounces
In standard form, the weight can be written as a decimal number between 1 and 10 multiplied by a power of 10.
1x10^(-3) in standard form is 0.001.
Therefore, the weight of the pitaya seed in standard form is 0.001.
The weight of a pitaya, or dragon fruit, is given as 1x10^3 ounces in scientific notation, which converts to 1000 ounces in standard form.
Explanation:Scientific notation is a concise way to express very large or small numbers, using powers of 10. In this case, the weight of a pitaya, represented as 1x10^3 ounces in scientific notation, can be easily converted into standard form. The exponent, 3 in this instance, indicates the number of places the decimal point should be moved. Therefore, an exponent of 3 means shifting the decimal point three places to the right. Consequently, the weight of the pitaya in standard form is 1000 ounces. This method provides a clear and efficient way to handle large numbers, making complex calculations and comparisons more manageable.
Learn more about Converting scientific notation to standard form here:https://brainly.com/question/15331767
#SPJ2
Related Questions
the zagat restaurant survey provides food, decor, and service ratings for some of the top restaurants across the united states. for 18 restaurants located in a certain city, the average price of a dinner, including one drink and tip, was $48.60. you are leaving on a business trip to this city and will eat dinner at three of these restaurants. your company will reimburse you for a maximum of $50 per dinner. business associates familiar with these restaurants have told you that the meal cost at one-third of these restaurants will exceed $50. suppose that you randomly select three of these restaurants for dinner. (round your answers to four decimal places.)
Answers
Based on the information given, let's find the probability that you will not exceed the $50 reimbursement limit for all three dinners.
1. First, identify the number of restaurants that exceed the $50 limit:
One-third of 18 restaurants is (1/3) * 18 = 6 restaurants.
2. Calculate the probability of selecting a restaurant that does not exceed the $50 limit:
There are 12 restaurants (18 total - 6 expensive ones) that meet the criteria. So, the probability of choosing one of them is 12/18 = 2/3.
3. Determine the probability of choosing three restaurants that do not exceed the $50 limit:
Since you're choosing three restaurants, we'll multiply the individual probabilities: (2/3) * (2/3) * (2/3) = 8/27.
4. Round the answer to four decimal places:
The probability is approximately 0.2963, or 29.63%.
So, if you randomly select three of these restaurants for dinner, there is a 29.63% chance that you will not exceed the $50 reimbursement limit for all three dinners.
To know more about probability visit :
https://brainly.com/question/32004014
#SPJ11
Helps me solve this problem please
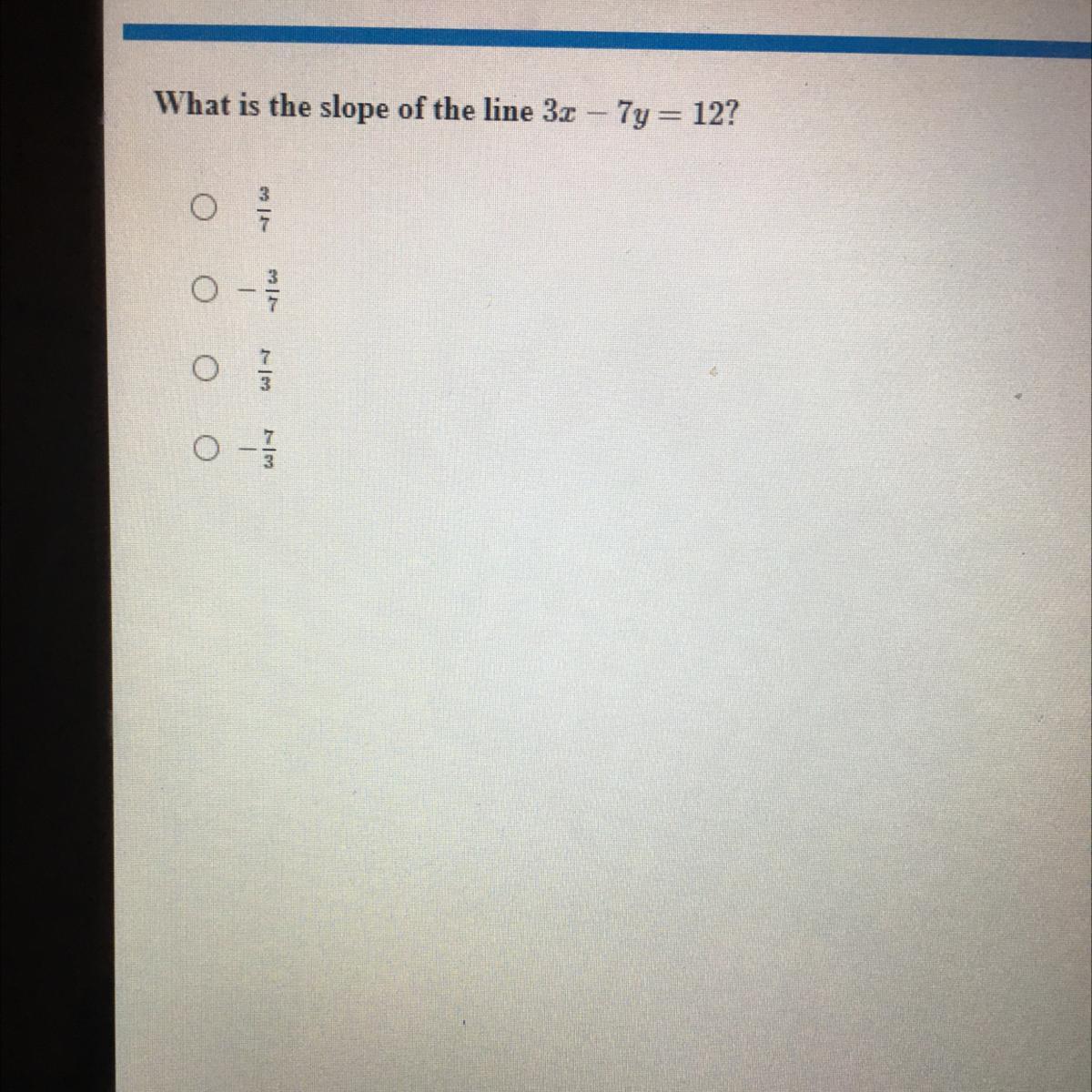
Answers
Answer:
The slope is -3/7 so B
Step-by-step explanation:
Just turn this into slope-intercept form.
what you do is subtract 3x so that it's moved to the right side.
It should look like this -7y = 12 - 3x
Then just divide all numbers by 7 so everything is simplified
It should look like this y = -3/7x - 12/7
pls mark brainliest because i didn't waste you time lol
The temperature went up by 5.C , then down by 3 ∘ C and finally an increase of 9 ∘ C , ending up at a temperature of 3 7 ∘ C. What was the starting temperature?
Answers
So, the starting temperature was 26.C.
Solve the equation:
M/4 +8=41

Answers
Answer:
m = 132
Step-by-step explanation:
(m / 4) + 8 = 41
(m / 4) = 33
m = 132
Step-by-step explanation:
m/4=33
m=33×4=132
,,,,,,,
On a distant planet, a ball is thrown upwards from ground level, reaching a maximum height of 12m and hitting the ground again in eight seconds. Determine a quadratic equation in the form ax^2 + bx^2+c = 0 that could be used to calculate when the ball is at a height of 3m. Do not solve the equation.
Answers
Answer:
(-3 ÷ 4)x^2 + 6x
Step-by-step explanation:
Data mentioned in the question
Maximum height = 12m
Number of seconds = 8
Height = 3m
Depend on the above information, the quadratic equation is shown below:
As it took 8 seconds to hit the maximum altitude and it reverted to the ground floor, this graph also reflects the motion in parabola after 4 seconds, so that the a must be negative
Now it is given that
a × x ^ 2 + bx + c =0
We can considered that
x = 0
x = 8
As {0.8} are intercepts of x
When x = 0, then it is
a × 0 ^ 2 + b(0) + c = 0 .................... (i)
Hence 0 = 0
Now x = 8, it is
a × 8 ^ 2 + b(8) + c = 0
Hence a(8)^2 + b(8) + c = 0 ..................(ii)
As it can be seen that in the first equation c must be zero
Whereas the second equation is
64a + 8b = 0
i.e.
8a = -b or a = -b ÷ 8
Now according to the quadratic function, it presented
(-b ÷8)x^2 + bx + 0
So, the parabola vertex is (4, 12)
Now place this in the place of a
(-b ÷ 8)(4)^2 + b(4) = 12
And for calculating this b, all terms must be multiplied by 8
That appears
-b(16) + 32b = 96
16b = 96
So, b = 6.
As a = -b ÷8
a = -6 ÷ 8
a = -3 ÷4
So, the equation is
= (-3 ÷ 4)x^2 + 6x
Hence, this is the equation
what is #2 ? In the figure shown , QP = 2x + 9 and QM = 5x - 3 FIND QN

Answers
Given:
\(QP=2x+9,QM=5x-3\)
To find:
The value of QN.
Solution:
From the figure it is clear that, point Q is the intersection point of angle bisectors. So, point Q is the incenter.
\(QP=QM=QN\) ...(i) [Incenter is equidistant from each side of triangle]
Using (i), we get
\(QP=QM\)
\(2x+9=5x-3\)
\(2x-5x=-9-3\)
\(-3x=-12\)
Divide both sides by -3.
\(x=4\)
Now,
\(QP=2x+9\)
\(QP=2(4)+9\)
\(QP=8+9\)
\(QP=17\)
Using (i), we get
\(QN=17\)
Therefore, the value of QN is 17.
Which distribution shape (skewed left, skewed right, or symmetric) is most likely to result in the mean being substantially smaller than the median?
Answers
A skewed right distribution is most likely to result in the mean being substantially smaller than the median.
The mean and median are measures of central tendency used to describe the center of a distribution. In a skewed right distribution, the tail of the distribution extends towards the right, indicating a larger number of smaller values and a few extremely large values. This distribution shape is also known as positively skewed.
When a distribution is skewed right, the mean is typically pulled towards the larger values in the tail, making it larger than the median. However, there are scenarios where the mean can be substantially smaller than the median in a skewed right distribution.
This occurs when there are extremely large values in the tail that significantly affect the mean, but the bulk of the distribution remains concentrated on the smaller side. As a result, the mean can be pulled downward, making it smaller than the median.
On the other hand, in a symmetric distribution or a skewed left distribution (negatively skewed), where the tail extends towards the left with a larger number of larger values and a few extremely small values, it is less likely for the mean to be substantially smaller than the median. In these cases, the mean is typically closer to or larger than the median.
To know more about skewed refer here:
https://brainly.com/question/32250442
#SPJ11
The radius of a circle is 8 millimeters. what's the circle's area
Answers
Use the equation formula to find the area of a circle
\(A=\pi\cdot r^2\)The radius is given on the question, replace this value on the equation and find the area.
\(\begin{gathered} A=\pi\cdot8^2 \\ A=\pi\cdot64 \\ A=201.06 \end{gathered}\)The area of the circle is 201.06 mm^2
1/4=something 8 plz help me
Answers
Answer:
1/4 = 0.25
Step-by-step explanation:
Answer:
2/8
Step-by-step explanation:
i don't know what to put here but 1/4 is = to 2/8
A worker earns $9 per hour and works 25 hours each week. If the worker receives a 3% pay increase, how much additional pay will the worker earn each week?
Answers
Answer: $6.75
Step-by-step explanation:
25 hours times $9= $225/week
3% increase from $9.00= $0.27
$9.27 times 25 hours= $231.75
$231.75-$225= $6.75 more per week
The temperature each hour in Elma, Texas on October 1 is modelled by the equation
t(h) = 10 cos(15h - 10)° + 30 where his hour of the day with 0 meaning midnight, and t is the
temperature in degrees Celsius. How hot did it get in Elma on October 1?
Answers
Answer:
\(39.8^{\circ} C\)
Step-by-step explanation:
We are given that the temperature each hour in Elma Texas on October 1 is modelled by the equation
\(t(h)=10cos(15h-10)^{\circ}+30\)
Where h=Hour of the day with 0 meaning midnight
t=Temperature in degree Celsius
We have to find the temperature on October 1.
Substitute h=0
\(t(0)=10cos(15(0)-10)+30\)
\(t(0)=10cos(-10)+30\)
\(t(0)=39.8^{\circ} C\)
Hence, the temperature in Elma on October 1=\(39.8^{\circ} C\)
please help ;-; -x^3+5x^2+6x=0 solve for x and show work
Answers
X= 0
Hope this is correct and good luckk!!!! :)
Answer:
x = 0, 6, -1
Step-by-step explanation:
To solve for x, first get rid of the negative x^3 by making it positive.
x^3 - 5x^2 - 6x = 0
Now you can start by finding the possible zeros. To do so take the factors of p (in this case the 6 in 6x) and the factors of q (in this case 1 in -x^3) and divide p by q.
P = ±1, ±2, ±3, ±6
Q = 1
possible zeros = ±1, ±2, ±3, ±6
Go through your equation x^3 - 5x^2 - 6x = 0 and check each possible zero until you find one that gets the equation to equal zero.
You could either continue to try each number and the ones that work would be your answer, or you can find one that works, factor it out, then factor your new equation. The second method is faster so that's what I'll use
Check each possible zero. For example:
(1)^3 - 5(1)^2 - 6(1) = 0
-10=0 This will not work
(-1)^3 - 5(-1)^2 - 6(-1) = 0
0 = 0
-1 Works, so now you will factor out -1 using synthetic division.
-1 | | 1 -5 -6 0
| -1 6 0
1 -6 0 0
Your new equation is x^2 - 6x = 0
Now factor your new equation:
x(x - 6) = 0
x = 0, 6, -1
I hope this all made sense, have a good day :)
I don't know this can someone help me?

Answers
Answer:
513.247
Step-by-step explanation:

2. How can you tell if a number is even or odd?
A. Look at the ones place.
B. Look at the tens place.
C. Look at the hundreds place.
D. Add o to the number.
Answers
Answer:
A.
bc if you have the answer 16 you look at 6 and see that 6 is a even number so the whole thing's even lol
Answer:
I think the answer is A
Step-by-step explanation
the most frequently used graphic in reports is the table true false
Answers
The statement the most frequently used graphic in reports is the table is false because tables are not typically the most frequently used graphic in reports.
While tables are commonly used in reports to present structured and detailed information, they are not typically the most frequently used graphic. Instead, other types of visuals such as charts, graphs, and diagrams are often employed to present data and communicate information more effectively.
Graphical representations like bar charts, line charts, pie charts, and scatter plots are widely used in reports to visualize patterns, trends, comparisons, and relationships in the data. These visualizations offer a concise and visually appealing way to convey information, making it easier for readers to understand complex data.
Tables, on the other hand, are more suitable for presenting precise numerical values, categorical information, or detailed breakdowns. They are useful for displaying large datasets or providing specific values for reference. However, their format can be dense and may require closer scrutiny, making them less visually impactful compared to graphical representations.
To know more about bar charts, refer here:
https://brainly.com/question/32121650
#SPJ11
For each of the following relations, decide if it is reflexive, symmetric, and or transitive.
Prove your answers.
(a) Ri is the relation on R given by Ri = {(z,y) ERx R: |x-y <1}.
(b) Let A be a set with at least two elements. Let R be the relation on A given by
(c) Rs is the relation on Z given by R3 = {(z,y) ⬠Zà Z: xy > 0).
(d) R, is the relation on Z given by R, = {(2, y) ⬠Zx Z: 3|(à + 2y)}. (e) Rs is the relation on Z given by Rs = {(x,y) ⬠Zx Z: there exists k ⬠N such that
elyk and yak).
Answers
In this question, we were given five relations and asked to determine if they are reflexive, symmetric, and/or transitive.
(a) The relation Ri on R is reflexive, symmetric, and transitive.
(b) The relation R on A is not reflexive, not symmetric, and transitive.
(c) The relation Rs on Z is not reflexive, not symmetric, and transitive.
(d) The relation R, on Z is not reflexive, not symmetric, and not transitive.
(e) The relation Rs on Z is reflexive, not symmetric, and transitive.
What is reflexive relation?A reflexive connection is a relationship between items of a set A in which each element is related to itself. As the name implies, the image of each element of the set is its own reflection. In set theory, a reflexive relation is an essential concept.
(a) Ri is reflexive, symmetric, and transitive.
- Reflexive: For any x ∈ R, (x, x) ∈ Ri since |x - x| = 0 < 1.
- Symmetric: For any (x, y) ∈ Ri, we have |x - y| < 1, which implies |y - x| < 1. Therefore, (y, x) ∈ Ri.
- Transitive: For any (x, y), (y, z) ∈ Ri, we have |x - y| < 1 and |y - z| < 1. Adding these inequalities, we get |x - z| < 2, which implies (x, z) ∈ Ri.
(b) R is not reflexive, symmetric, or transitive.
- Not reflexive: For any x ∈ A, (x, x) ∉ R since x - x = 0 is not a positive integer.
- Not symmetric: For any distinct x, y ∈ A, if (x, y) ∈ R, then x - y = 1, which implies y - x = -1 is not a positive integer. Therefore, (y, x) ∉ R.
- Not transitive: Let A = {1, 2, 3} and R = {(1, 2), (2, 3)}. Then (1, 3) is not in R since 3 - 1 = 2 is not a positive integer.
(c) R3 is not reflexive, symmetric, or transitive.
- Not reflexive: For any x ∈ Z, (x, x) ∉ R3 since x * x = x^2 is not greater than 0.
- Symmetric: For any (x, y) ∈ R3, we have xy > 0, which implies yx > 0. Therefore, (y, x) ∈ R3.
- Not transitive: Let x = -1, y = 2, and z = -1. Then (x, y) ∈ R3 and (y, z) ∈ R3, but (x, z) = (-1, -1) ∉ R3 since xz = 1 is not greater than 0.
(d) R, is not reflexive, symmetric, or transitive.
- Not reflexive: For any y ∈ Z, (y, y) ∉ R, since 3 does not divide y + 2y = 3y.
- Not symmetric: For y = 1 and z = 2, we have (2, 1) ∉ R, but (1, 2) ∈ R since 3 divides 1 + 4 = 5.
- Not transitive: Let x = 2, y = 1, and z = 5. Then (x, y) ∈ R, (y, z) ∈ R, but (x, z) = (2, 5) ∉ R since 3 does not divide 2 + 10 = 12.
(e) Rs is the relation on Z given by Rs = {(x,y) ⬠Zx Z: there exists k ⬠N such that elyk and yak).
- Reflexive: This relation is not reflexive because (1, 1) ∉ Rs as there does not exist k such that 1 x k = 1.
- Symmetric: This relation is not symmetric because, for example, (1, 2) ∈ Rs but (2, 1) ∉ Rs since there does not exist k such that 2 x k = 1.
- Transitive: This relation is not transitive. For example, let x = 1, y = 2, and z = 4. Then (x, y) ∈ Rs and (y, z) ∈ Rs, but (x, z) ∉ Rs since there does not exist k such that 1 x k = 4.
In short, in this question, we were given five relations and asked to determine if they are reflexive, symmetric, and/or transitive.
(a) The relation Ri on R is reflexive, symmetric, and transitive.
(b) The relation R on A is not reflexive, not symmetric, and transitive.
(c) The relation Rs on Z is not reflexive, not symmetric, and transitive.
(d) The relation R, on Z is not reflexive, not symmetric, and not transitive.
(e) The relation Rs on Z is reflexive, not symmetric, and transitive.
Learn more about reflexive relation on:
https://brainly.com/question/30105703
#SPJ4
Use the Chain Rule to find dw/dt. w = xey/z, x = t3, y = 3 - t, z = 7 + 3t = dw dt Use the Chain Rule to find dw/dt. w = In( vx2 + y2 + z2), X = 2 sin(t), x = 2 sin(t), y = 4 cos(t), z = 5 tan(t) Use the Chain Rule to find az/as and az/at. z = tan(u/v), u = 7s + 9t, V = 9s - 7t The length l, width w, and height h of a box change with time. At a certain instant the dimensions are l = 9 m and w = h = 5 m, and land w are increasing at a rate of 7 m/s while h is decreasing at a rate of 4 m/s. At that instant find the rates at which the following quantities are changing. (a) The volume. m3/s (b) The surface area. m²/s (c) The length of a diagonal. (Round your answer to two decimal places.) m/s
Answers
Using the Chain Rule to find dw/dt:
We have w = xey/z, where x = t^3, y = 3 - t, and z = 7 + 3t. To find dw/dt, we can use the Chain Rule:
dw/dt = (∂w/∂x)(dx/dt) + (∂w/∂y)(dy/dt) + (∂w/∂z)(dz/dt)
Taking the partial derivatives of w with respect to x, y, and z, we get:
∂w/∂x = ey/z * 3t^2
∂w/∂y = ex/z * (-1)
∂w/∂z = -exy/z^2
Substituting in the values for x, y, and z, we get:
∂w/∂x = (3t^2)(3-t)/(7+3t)
∂w/∂y = -(t^3)(3-t)/(7+3t)
∂w/∂z = -(t^3)(3-t)(3+7t)/(7+3t)^2
Taking the derivatives of x, y, and z with respect to t, we get:
dx/dt = 3t^2
dy/dt = -1
dz/dt = 3
Substituting in all the values, we get:
dw/dt = (3t^2)(3-t)/(7+3t) + -(t^3)(3-t)/(7+3t) + -(t^3)(3-t)(3+7t)/(7+3t)^2
Simplifying this expression, we get:
dw/dt = (-3t^4 + 9t^3 + 3t^2 - 9t)/(7+3t)^2
Using the Chain Rule to find dw/dt:
We have w = ln(vx^2 + y^2 + z^2), where x = 2sin(t), y = 4cos(t), and z = 5tan(t). To find dw/dt, we can use the Chain Rule:
dw/dt = (∂w/∂x)(dx/dt) + (∂w/∂y)(dy/dt) + (∂w/∂z)(dz/dt)
Taking the partial derivatives of w with respect to x, y, and z, we get:
∂w/∂x = 2vx^2/(vx^2 + y^2 + z^2)
∂w/∂y = 2vy/(vx^2 + y^2 + z^2)
∂w/∂z = 2vz/(vx^2 + y^2 + z^2)
Substituting in the values for x, y, and z, we get:
∂w/∂x = 4vsin(t)^2/(v(sin(t)^2 + cos(t)^2 + 25tan(t)^2))
∂w/∂y = 8vcos(t)/(v(sin(t)^2 + cos(t)^2 + 25tan(t)^2))
∂w/∂z = 10vtan(t)/(v(sin(t)^2 + cos(t)^2 + 25tan(t)^2))
Taking the derivatives of x, y, and z with respect to t, we get:
dx/dt = 4cos(t)
dy/dt = -4sin(t)
dz/dt = 5sec^2(t)
Substituting in all the values, we get:
dw/dt = (4vsin(t)^2)/(v(sin(t)^2 + cos(t)^2 + 25tan(t)^2)) + (8vcos(t))/(v(sin(t)^2 + cos(t)^2 + 25tan(t)^2)) + (10vtan(t))/(v(sin(t)^2 + cos(t)^2 + 25tan(t)^2))
Simplifying this expression, we get:
dw/dt = (16vsin(t)cos(t) - 32vcos(t)sin(t) + 50vtan(t)sec^2(t))/(sin(t)^2 + cos(t)^2 + 25tan(t)^2)^2
Using the Chain Rule to find az/as and az/at:
We have z = tan(u/v), where u = 7s + 9t and v = 9s - 7t. To find az/as and az/at, we can use the Chain Rule:
az/as = (∂z/∂u)(du/ds) + (∂z/∂v)(dv/ds)
az/at = (∂z/∂u)(du/dt) + (∂z/∂v)(dv/dt)
Taking the partial derivatives of z with respect to u and v, we get:
∂z/∂u = sec^2(u/v)(1/v)
∂z/∂v = -sec^2(u/v)(u/v^2)
Taking the derivatives of u and v with respect to s and t, we get:
du/ds = 7
dv/ds = 9
du/dt = 9
dv/dt = -7
Substituting in all the values, we get:
az/as = (sec^2(u/v)(1/v))(7) + (-sec^2(u/v)(u/v^2))(9)
az/at = (sec^2(u/v)(1/v))(9) + (-sec^2(u/v)(u/v^2))(-7)
Substituting in the expression for u and v, we get:
az/as = (sec^2((7s+9t)/(9s-7t))(1/(9s-7t)))(7) + (-sec^2((7s+9t)/(9s-7t))((7s+9t)/(9s-7t)^2))(9)
az/at = (sec^2((7s+9t)/(9s-7t))(1/(9s-7t)))(9) + (-sec^2((7s+9t)/(9s-7t))((7s+9t)/(9s-7t)^2))(-7)
Finding the rates of change of volume, surface area, and length of diagonal of a box:
At a certain instant, the dimensions of the box are l = 9 m, w = h = 5 m, and l and w are increasing at a rate of 7 m/s while h is decreasing at a rate of 4 m/s.
(a) To find the rate at which the volume is changing, we can use the formula for the volume of a box:
V = lwh
Taking the derivative of V with respect to time, we get:
dV/dt = (dh/dt)lwh + (dl/dt)wh + (dw/dt)lh
Substituting in the values for l, w, and h, as well as the rates of change for l, w, and h, we get:
dV/dt = (-4)(9)(5)(5) + (7)(5)(5)(9) + (7)(9)(5)(5)
Simplifying this expression, we get:
dV/dt = 385 m^3/s
Therefore, the volume of the box is increasing at a rate of 385 m^3/s at that instant.
(b) To find the rate at which the surface area is changing, we can use the formula for the surface area of a box:
S = 2lw + 2lh + 2wh
Taking the derivative of S with respect to time, we get:
dS/dt = (dl/dt)(2w + 2h) + (dh/dt)(2l + 2w) + (dw/dt)(2l + 2h)
Substituting in the values for l, w, and h, as well as the rates of change for l, w, and h, we get:
dS/dt = (7)(2(5) + 2(5)) + (-4)(2(9) + 2(5)) + (7)(2(9) + 2(5))
Simplifying this expression, we get:
dS/dt = 164 m^2/s
Therefore, the surface area of the box is increasing at a rate of 164 m^2/s at that instant.
(c) To find the rate at which the length of the diagonal is changing, we can use the formula for the length of the diagonal of a box:
D = sqrt(l^2 + w^2 + h^2)
Taking the derivative of D with respect to time, we get:
dD/dt = (1/2)(l^2 + w^2 + h^2)^(-1/2)(2l(dl/dt) + 2w(dw/dt) + 2h(dh/dt))
Substituting in the values for l, w, and h, as well as the rates of change for l, w, and h, we get:
dD/dt = (1/2)(9^2 + 5^2 + 5^2)^(-1/2)(2(9)(7) + 2(5)(7) + 2(5)(-4))
Simplifying this expression, we get:
dD/dt = 3.08 m/s
Therefore, the length of the diagonal of the box is increasing at a rate of 3.08 m/s at that instant.
Visit here to learn more about partial derivatives brainly.com/question/30365299
#SPJ11
My number is the smallest 2 digit number that only has 2 factors
Answers
Answer:
11
Step-by-step explanation:
Consider 10's factors: 1, 2, 5, 10, this is more than 2.
11's factors: 1, 11 (!)
Answer:
I think11 js the smallest 2 digit number that only has 2 factors
Howard, in his new lightweight running shoes, was able to walk at the rate of
meters per second. His coach timed his walking at this steady pace for
seconds. How far did he walk during that time? Use paper and a pencil to show your work, and then check your answer with a calculator.
Answers
If Howard, in his new lightweight running shoes, was able to walk at the rate of 0.83 meters per second in which his coach timed his walking at this steady pace for seconds. . The distance he walk during that time is 10.126.
How to find the distance?Given data:
Distance walk in 1 second = 0.83 meters per second
Walk at steady pace = 12.2 seconds
Now let find the distance that Howard have to walked in 12.2 seconds
Distance walked in 12.2 seconds = 0.83 meters per second × 12.2 seconds
Distance walked in 12.2 seconds = 10.126
Therefore the distance is 10.126.
Learn more about distance here:https://brainly.com/question/26046491
#SPJ1
The complete question is:
Howard, in his new lightweight running shoes, was able to walk at the rate of 0.83 meters per second. His coach timed his walking at this steady pace for 12.2 seconds. How far did he walk during that time? Use paper and a pencil to show your work, and then check your answer with a calculator.
If function ghas the factors (x-7) and (x + 6), what are the zeros of function g?
Answers
Answer:
x = 7, -6
Step-by-step explanation:
Since they already give you the binomial factors, all you need to do is set them equal to 0 to find your roots:
x - 7 = 0
x = 7
x + 6 = 0
x = -6
Answer:
The zeros are 7 and -6Step-by-step explanation:
(x-7)(x+6)=0
x-7=0/(x+6)
x cannot be -6
x-7=0
x=7
x+6=0/(x-7)
x+6=0
x=-6
The zeros are 7 and -6
factorise the expression 6x²y + 15xy²
Answers
Which equation represents a line passing through the points (0, 1) and (2, -3)?
Answers
The equation of the line passing through the points (0, 1) and (2, -3) is y = -2x + 1.
What is the equation of the line?The formula for equation of line is expressed as;
y = mx + b
Where m is slope and b is y-intercept.
First, we determine the slope of the line.
Given the two points are (0, 1) and (2, -3).
We can find the slope of the line by using the slope formula:
m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Substituting the values, we get:
m = (-3 - 1) / (2 - 0)
m = -4 / 2
m = -2
Using the point-slope form, plug in one of the given points and slope m = -2 to find the equation of the line.
Let's use the point (0, 1):
y - y₁ = m(x - x₁)
y - 1 = -2(x - 0)
y - 1 = -2x
y = -2x + 1
Therefore, the equation of the line is y = -2x + 1.
Learn more about equation of line here: brainly.com/question/2564656
#SPJ1
help on this pls any help would be appreciated

Answers
Answer:
y = 3x + 2
Step-by-step explanation:
For this question we have to use the equation y=mx+c
m represents the gradient
c represents where the line crosses the y-axis (the y-intercept)
1) Find the gradient
To find the gradient we have to divide the change in y by change in x
In this question that means we have to divide 3 by 1
3 ÷ 1 = 3
2) Find the y-intercept
We can see that the line crosses the y-axis on the point (0,2) meaning the y-intercept is 2
y = 3x + 2
Hope this helps, have a lovely day! :)
Answer:
Step-by-step explanation:
y=3x+2
5 $17.00 3-66. Randall and Stephano work in a restaurant. Randall earned $27.50 one day, $25.00 the next day, and $32.50 on the third day. Stephano works fewer hours, but more days. He earned $17.50 one day, $22.50 the next day, $12.50 the third day, $15.00 the fourth day, and $17.00 the fifth day. Who earned the most money? How much more?
Answers
Answer:
Randall and the most money. she earned 50 cents more than Stephano did.
Step-by-step explanation:
so it's Randall makes $27.50 on his first day and $25 on a second date and and 32.50 on his third day you would add those up to get $85 in all. now Stefano gets 7.50 22.50 12.50 15.00 and 17.00 dollars , and when you add all those together he gets 84.50 and all. meaning that random made more money by .50 cents.
A line plot with Kelly's ribbon lengths is shown .she adds two more ribbons so that the total length of ribbon is 200 inches . What are two possible lengths of ribbon, in inches , that Kelly could have added

Answers
Answer: (I changed it back to fraction form instead of decimal because it seems that is how you are doing it)
Two possible lengths of ribbon (In inches) are 25 and 133 3/4
Step-by-step explanation:
Okay, so- First, You need to find out how much ribbon is there before the two additional ones are added. Like this:
12 + 14 2/4 + 14 3/4 = 41 1/4
Next, subtract that amount from 200 to get the number of inches of ribbon that are needed to get 200 inches of ribbon. Like this:
(I changed it to a decimal to make it easier, so don't mind that)
200 - 41.25 = 158.75
So, 158.75 inches of ribbon are needed to get 200 inches. You can subtract any number less than 158.75 from that to get two seperate ribbon measurements.
(This might sound confusing so here)
For example:
158.75 - 25 = 133.75 (The bolded numbers are the two measurements)
158.75 - 65 = 93.75
So, Two possible lengths (in inches) of ribbon that kelly could have added are "25" and "133.75 "
Two possible lengths (in inches) of ribbon that kelly could have added are also "65" and "93.75"
Hope this helps! Please tell me if you have any questions!
Tina´s family is taking a road trip. If they travel for 3.5 hours on the first day, 2 hours on the second day 4.5 hours on the third day, and 4 hours on the fourth day, how long did they drive overall
Answers
Answer:
14.
Step-by-step explanation:
this a addition problem since it says "overall".
you simply add them.
There is a ratio of 2 cats to every 3 dogs, if this rate continues how many dogs are there if there are 22 cats?
Answers
Answer:
33 dogs
Step-by-step explanation:
By taking the 22 cats and dividing it by the ratio. Then multiply that quotient by the ratio of dogs.
Thus:
22/2 = 11
11*3 = 33
There will be 33 dogs.
Hope This Helps :)
Answer: 33
Step-by-step explanation:
2cats = 3dogs
22cats = x
Cross multiply
2x = 3×22
2x = 66
x = 66/2
x = 33
let e be the 4 by 4 elementary matrix corresponding to the row operation then e is identical to at every entry except at the entry on row number_______ and column number_______ where the entry in e is________ .
Answers
The entry in the elementary matrix e, corresponding to the row operation -6R2+R4 -> R4, is located in row number 4 and column number 2, and its value is -6.
To construct the elementary matrix e, we start with the 4 by 4 identity matrix I4 and perform the row operation -6R2+R4 -> R4. The row operation is equivalent to multiplying the second row of I4 by -6 and adding the result to the fourth row. This can be represented by the following matrix:
[1 0 0 0]
[0 1 0 0]
[0 -6 1 0]
[0 0 0 1]
Thus, the entry in row 4 and column 2 is -6, and all other entries in e are identical to those in I4.
Learn more about Matrix:
https://brainly.com/question/2456804
#SPJ4
Complete Question:
let e be the 4 by 4 elementary matrix corresponding to the row operation -6R2+R4 -> R4 then e is identical to I4 at every entry except at the entry on row number_______ and column number_______ where the entry in e is________.
6 Sasha thinks of a number.
She adds 1 to her number then multiplies the result by 5.
a Use a mapping to write this as a function.
The answer Sasha gets is 11.
b Use inverse functions to work out the number Sasha thought of in the beginning.
Show all your working.
Answers
sin(2x)cos(7x) - cos(2x)sin(7x) = 0.1
Answers
Answer:
x≈-0.0200335+2kπ/5
x≈-0.648352+2kπ/5
Step-by-step explanation:
sin(-5x)=0.1
-sin(5x)=0.1
sin(5x)=-0.1
sin(5x)=1/10
5x=arcsin(- 1/10)
5x=π-arcsin(- 1/10)
5x=π-arcsin(- 1/10)
5x=π-arcsin(- 1/10)+2kπ
5x=π-arcsin(- 1/10)+2kπ
x=arcsin (1/10)/5 + 2kπ/5
x=arcsin (1/10)/5 + 2kπ/5
x≈-0.0200335+2kπ/5
x≈-0.648352+2kπ/5