A polling company plans to create a probability model for a state election. In a telephone survey of 750 residents who stated they were registered to vote, they found that 318 planned to vote for the Democratic candidate, 268 planned to vote for the Republican candidate, with the remainder were undecided. What is a reasonable probability model for the state election?
Answers
The reasonable probability model for the state election is
21.87% residents are undefined votes35.73 resident plan to vote for Republican candidate 42.40% residents plan to vote for Democratic candidateTotal number of residents = 750
The number of residents that planned to vote for the Democratic candidate = 318
The percentage = (318 / 750) × 100
= 42.40%
The number of residents that planned to vote for the Republican candidate = 268
The percentage = (268/750) × 100
= 35.73%
Number of undecided votes = 750 - (318+268)
= 750 - 586
=164
The percentage = (164 / 750) × 100
= 21.87%
Hence, the reasonable probability model for the state election is
21.87% residents are undefined 35.73 resident plan to vote for Republican candidate 42.40% residents plan to vote for Democratic candidateLearn more about probability model here
brainly.com/question/11736456
#SPJ4
Related Questions
11. Engineering The maximum load for a certain elevator is 2000 pounds. The total
weight of the passengers on the elevator is 1400 pounds. A delivery man who weighs
243 pounds enters the elevator with a crate of weight w. Write, solve, and graph an
inequality to show the values of w that will not exceed the weight limit of the elevator.
Answers
The inequality to show the values of [w] that will not exceed the weight limit of the elevator is w + 1643 ≤ 2000. On solving the inequality, we get w ≤ 357. The graph of the inequality is attached.
What is inequality?In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size.An inequality is a mathematical relationship between two expressions and is represented using one of the following -≤ : less than or equal to
≥ : greater than or equal to
< : less than
> : greater than
≠ : not equal to
Given is the maximum load for a certain elevator is 2000 pounds. The total weight of the passengers on the elevator is 1400 pounds. A delivery man who weighs 243 pounds enters the elevator with a crate of weight [w].
We can write the inequality as follows -1400 + 243 + w ≤ 2000
w + 1643 ≤ 2000
Solving the inequality, we get -w + 1643 ≤ 2000
w ≤ 2000 - 1643
w ≤ 357
Refer to the graph attached.Therefore, the inequality to show the values of [w] that will not exceed the weight limit of the elevator is w + 1643 ≤ 2000. On solving the inequality, we get w ≤ 357. The graph of the inequality is attached.
To solve more questions on inequalities, we get -
https://brainly.com/question/11897796
#SPJ1

is vertical and passes through (-4, 6)
Answers
Answer:
x = -4
Step-by-step explanation:
If the line is vertical, it will only go through one x value/coordinate
This means the equation will be in the form x =
Since the point given has the x coordinate of -4, this means that -4 is the only x value that the line will pass through.
So, the equation of this line is x = -4
given f(x)= -x^2+2x+6, find f(-7)
Answers
The value of f(-7) in the given function, f(x) = -x^2 + 2x + 6, is -57
Determining the value of a given functionFrom the question, we are to determine the value of f(-7) in the given function
The given function is
f(x) = -x^2 + 2x + 6
To find the value of f(-7) in the given function,
We will substitute -7 for x in the expression for f(x) and evaluate the resulting expression
That is,
f(x) = -x^2 + 2x + 6
f(-7) = -(-7)^2 + 2(-7) + 6
Simplifying this expression gives:
f(-7) = -49 - 14 + 6
f(-7)= -57
Hence, the value of f(-7) is -57
Learn more on Determining the value of a function here: https://brainly.com/question/8334128
#SPJ1
Suppose that four students, Stephanie, Charles, Tim, and Rachel, are all preparing to take standardized exam that contains three subjects, math, reading, and science. Four tutors are available to help the students prepare for the exam. Each tutor is able to help in any of the three subjects. How many different ways can the students, tutors, and subjects be uniquely combined?
Answers
Answer:
48 different ways
Step-by-step explanation:
To solve this question, we use the Fundamental Counting Principle technique.
Fundamental Counting Principle can be defined as the way by which we determine the possibility or the number of possible outcomes for an event.
If we have event X and event Y and event Z, then the number of possible outcomes = X × Y × Z
For the above question, we have 3 events
Event 1 : 4 students ( Stephanie, Charles, Tim, and Rachel)
Event 2: 3 subjects ( Math, Reading, And Science)
Event 3 : 4 tutors.
Therefore,the many different ways can the students, tutors, and subjects can be be uniquely combined is:
= 4 × 3 × 4
= 48 different ways
This is due today pls help. I’ll give u BRAINLIEST

Answers
Answer:
what do they a's and s's stand for?? (in the answer choices)
Step-by-step explanation:
a can of soda is placed inside a cooler. as the soda cools, its temperature in degrees celsius is given by the following function, where is the number of minutes since the can was placed in the cooler. find the temperature of the soda after minutes and after minutes. round your answers to the nearest degree as necessary.
Answers
The temperature of the soda after 20 minutes is approximately -18 degrees Celsius. To find the initial temperature of the soda, we can evaluate the function T(x) at x = 0.
Substitute x = 0 into the function T(x):
T(0) = -19 + 39e^(-0.45*0).
Simplify the expression:
T(0) = -19 + 39e^0.
Since e^0 equals 1, the expression simplifies to:
T(0) = -19 + 39.
Calculate the sum:
T(0) = 20.
Therefore, the initial temperature of the soda is 20 degrees Celsius.
To find the temperature of the soda after 20 minutes, we substitute x = 20 into the function T(x):
Substitute x = 20 into the function T(x):
T(20) = -19 + 39e^(-0.45*20).
Simplify the expression:
T(20) = -19 + 39e^(-9).
Use a calculator to evaluate the exponential term:
T(20) = -19 + 39 * 0.00012341.
Calculate the sum:
T(20) ≈ -19 + 0.00480599.
Round the answer to the nearest degree:
T(20) ≈ -19 + 1.
Therefore, the temperature of the soda after 20 minutes is approximately -18 degrees Celsius.
To learn more about function click here:
brainly.com/question/30721594
#SPJ11
INCOMPLETE QUESTION
A can of soda is placed inside a cooler. As the soda cools, its temperature Tx in degrees Celsius is given by the following function, where x is the number of minutes since the can was placed in the cooler. T(x)= -19 +39e-0.45x. Find the initial temperature of the soda and its temperature after 20 minutes. Round your answers to the nearest degree as necessary.
you train a ridge regression model, you get a r^2 of 1 on your training data and you get a r^2 of 0 on your validation data; what should you do?
Answers
In case of different values of cofficient of determination, r² during training and validation represents our regression model is overfitting, so increase the parameter alpha. So, option(a) is right.
The regression model using the normal L₁ technique is called Lasso Regression, and the model using L2 is called Ridge. Ridge regression reduces all regression coefficients to zero. We have a ridge regression training model, during data training, regression coefficient R² = 1
during data validation, regression coefficient R² = 0
R-squared is a suitable measure for linear regression models. This analysis shows the percentage of variance in the variable that the independent variables explain together. Here, R² = 1, shows model is good to fit but R² = 0, shows model is not fit to good. If the R²(test) ≪R²(training), then it indicates that your model does not generalize well. Then we can say model is overfitting state. So, option (b) represents right step to do.
For more information about regression model, visit:
https://brainly.com/question/29657622
#SPJ4
Complete question:
you train a ridge regression model, you get a R^2 of 1 on your training data and you get a R^2 of 0 on your validation data; what should you do?
a) Your model is underfitting, so increase the parameter alpha.
b) Your model is overfitting, so increase the parameter alpha
c) Your model is under fitting; so perform a polynomial transform
d) Nothing, your model performs flawlessly on your validation data
Assume there is a sample of n
1
=4, with the sample mean
X
1
=35 and a sample standard deviation of S
1
=4, and there is an independent sample of n
2
=5 from another population with a sample mean of
X
ˉ
2
=31 and a sample standard deviation S
2
=5. In performing the pooled-variance t test, how many degrees of freedom are there? There are degrees of freedom. (Simplify your answer.)
Answers
There are 7 degrees of freedom.
In performing the pooled-variance t test, the degrees of freedom can be calculated using the formula:
df = (n1 - 1) + (n2 - 1)
Substituting the given values:
df = (4 - 1) + (5 - 1)
df = 3 + 4
df = 7
Therefore, there are 7 degrees of freedom.
Learn more about degrees of freedom
brainly.com/question/32093315
#SPJ11
There are 7 degrees of freedom for the pooled-variance t-test.
To perform a pooled-variance t-test, we need to calculate the degrees of freedom. The formula for degrees of freedom in a pooled-variance t-test is:
\(\[\text{{df}} = n_1 + n_2 - 2\]\)
where \(\(n_1\)\) and \(\(n_2\)\) are the sample sizes of the two independent samples.
In this case, \(\(n_1 = 4\)\) and \(\(n_2 = 5\)\). Substituting these values into the formula, we get:
\(\[\text{{df}} = 4 + 5 - 2 = 7\]\)
In a pooled-variance t-test, we combine the sample variances from two independent samples to estimate the population variance. The degrees of freedom for this test are calculated using the formula \(df = n1 + n2 - 2\), where \(n_1\)and \(n_2\) are the sample sizes of the two independent samples.
To understand why the formula is \(df = n1 + n2 - 2\), we need to consider the concept of degrees of freedom. Degrees of freedom represent the number of independent pieces of information available to estimate a parameter. In the case of a pooled-variance t-test, we subtract 2 from the total sample sizes because we use two sample means to estimate the population means, thereby reducing the degrees of freedom by 2.
In this specific case, the sample sizes are \(n1 = 4\) and \(n2 = 5\). Plugging these values into the formula gives us \(df = 4 + 5 - 2 = 7\). Hence, there are 7 degrees of freedom for the pooled-variance t-test.
Therefore, there are 7 degrees of freedom for the pooled-variance t-test.
Learn more about t-test
https://brainly.com/question/13800886
#SPJ11
Need helppppp I’m stuckkkk
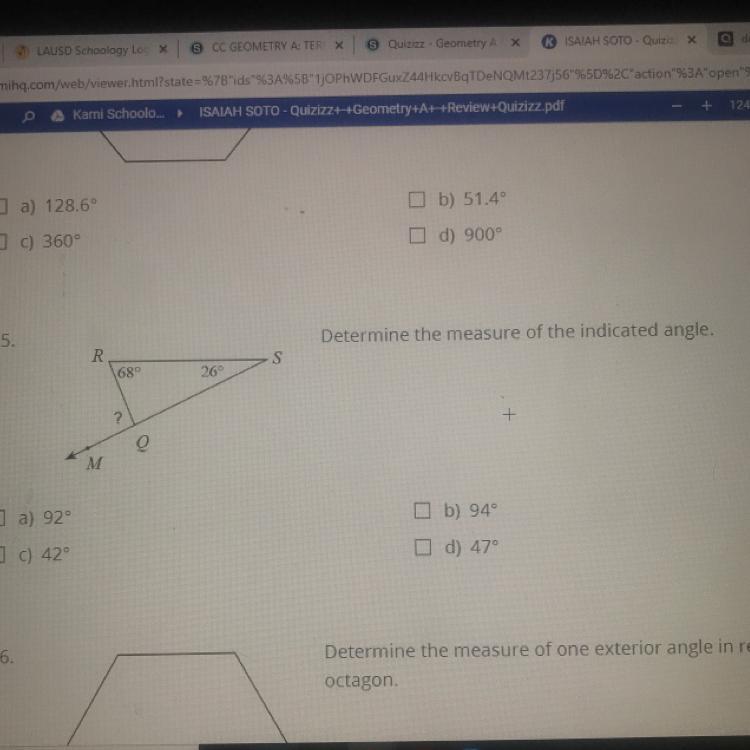
Answers
Answer:
b) 94
Step-by-step explanation:
The Total Degree of a Triangle is 180 degrees. Knowing this, set up an equation.
68+26+x=180.
x is the complementary angle of the "?" angle.
Solve the equation.
94+x=180
x=86
Then Subtract 86 from 180 to find "?"
180-86=94
I hope this helps!
Answer:
94;b
Step-by-step explanation:
68+26=94. 180-94=86. 180-86=94.
a circular harkness table is placed in a corner of a room so that it touches both walls. a mark is made on the edge of the table, exactly 18 inches from one wall and 25 inches from the other. what is the radius of the table?
Answers
The radius of table can be 13 inches or 73 inches.
Let r inches be the table's radius.
Make the corner the starting point or origin.
the coordinates for the table's center are as follows: (r, r).
So \((x-r)^{2} +(y-r)^{2}=r^{2}\) is the equation for the table's diameter.
The distance between the mark at the table's edge and one wall is 18 inches and 25 inches, respectively. Consequently, this point's coordinates are (18, 25). It might alternatively be (25, 18), but our calculations would not be affected.
Given that the mark is on the edge, it satisfies the criteria established by the table's circumference equation.
\((18-r)^{2} +(25-r)^{2} =x^{2}\)
\(324-36r+r^{2} +625-50r+x^{2} =x^{2}\)
\(r^{2} -86r+949=0\)
(r−13)(r−73)=0
r=13 inches or r=73 inches
As a result, the table's radius can be either 13 inches or 73 inches.
To learn more about radius here:
https://brainly.com/question/13449316
#SPJ4
Find the total surface area of the figure.

Answers
Answer:
8x6x4=192. So, the answer is 192.
$8,000 is invested in an account earning 7.9% interest (APR), compounded continuously. Write a function showing the value of the account after tt years, where the annual growth rate can be found from a constant in the function. Round all coefficients in the function to four decimal places. Also, determine the percentage of growth per year (APY), to the nearest hundredth of a percent.
Answers
The continuous compounding equation shown the value of the account after t years is given as follows:
\(A(t) = 8000e^{0.079t}\)
The percentage of growth per year (APY) is of 8.22%.
Continuous compounding
The balance of an account after t years of continuous compounding is given by the equation presented as follows:
\(A(t) = A(0)e^{kt}\)
In which the variables of the equation are described as follows:
A(0) is the initial balance of the account, the initial amount invested.k is the exponential interest rate earned by the account in each compounding period.In the context of this problem, the values of these parameters are given as follows:
A(0) = 8000, k = 0.079.
Hence the equation is:
\(A(t) = 8000e^{0.079t}\)
The percentage of growth per year (APY) is calculated as follows:
\(e^{k} - 1 = e^{0.079} - 1 = 1.0822 - 1 = 0.0822 = 8.22\%\)
More can be learned about continuous compounding at https://brainly.com/question/7513822
#SPJ1
Write the number 347.85 in expanded form. a 3 + 100 + 4 x 10 + 7 x 1 x 8 x (1/100) + 5 x (1/100) b 3 x 100 + 4 + 10 + 7 x 1 + 8 x (1/100) + 5 x (1/10) c 3 x 100 + 4 x 10 + 7 x 1 + 8 x (1/10) + 5 x (1/100)
Answers
Answer:
C. 3 × 100 + 4 × 10 + 7 × 1 + 8 × (1/10) + 5 × (1/100)
Step-by-step explanation:
3: hundreds
4: tens
7: ones
8: tenths
5: hundreths
2/3(6c+4)-(8c-5)
No spaces in your answer.
Do not change improper fractions to mixed numbers, type them as improper fractions in simplest form.
Answers
Answer:
Your answer is: \(-4c+23/3\)
Simplify the expression.
Step-by-step explanation:
Hope this helped : )
1. Use the spinner at the right, which is divided into equal sections, to detemine the following probability. P(brown or greater than 9)
2. Using a green number cube and a blue number cube, find the following probability. P(green less than 9 and blue greater than 3)
3. You choose a tile at random from a bag containing 5 A's, 2 B's, and 3 C's. You replace the first tile in the bag and then choose again. Find P(C and C). Question content area bottom Part 1 P(C and C)=enter your response here
4. You pick a coin at random from the set shown at the right, and then pick a second coin without replacing the first. Find the probability. P(penny then nickel)

Answers
Using it's concept, the probability is calculated as follows:
P(brown or greater than 9) = 3/5.
What is a probability?The probability of an event in an experiment is calculated as the number of desired outcomes of the experiment divided by the number of total outcomes of the experiment.
In the context of this problem, we have that:
The desired outcomes are the five brown regions, plus the green region with the number 10, which is a number greater than 9.The total outcomes are the 10 regions of the spinner.The desired probability is calculated as follows:
P(brown or greater than 9) = 6/10 = 3/5.
Both 6 and 10 can be simplified by 5, hence the simplified probability is of 3/5.
More can be learned about probabilities at https://brainly.com/question/14398287
#SPJ1
Mickey is classifying a quadrilateral with vertices at Q1,1, U(-1,-3), A(1,-4), D(3,0). What type of quadrilateral is it? Also why?
Please Help!
Answers
This quadrilateral is a trapezoid because it has one pair of parallel sides. The sides Q1U and AD are parallel, while the other two sides (U1 and DA) are not.
What is trapezoid?A trapezoid is a four-sided shape with two parallel sides, called the bases, and two non-parallel sides, called the legs. The opposing angles of the trapezoid are equal in measure, and the two adjacent angles are supplementary. A trapezoid can also be defined as a quadrilateral with exactly one pair of parallel sides. Trapezoids are often used in mathematics to define and calculate area, perimeter and other geometric properties. They can also be used to construct shapes and patterns in architecture, engineering and design.
To learn more about trapezoid
https://brainly.com/question/1410008
#SPJ1
Answer:
I'm pretty sure it's a rectangle
Step-by-step explanation:
the reason why is because there are 2 pairs that are equal to each other but each seem to be perpendicular in slope form.
b) You are saving for a vacation by taking $100 out of your paycheck each month and putting it into a savings account that pays 3% nominal interest, compounded monthly. How long will it take for you to be able to take that $3,000 vacation?
c) What is the equivalent effective interest rate for a nominal rate of 5% that is compounded...
i. Semi-annually
ii. Quarterly
Daily
iv. Continuously
Answers
b) It will take approximately 24.6 years to save $3,000 for your vacation by saving $100 each month with a 3% nominal interest rate compounded monthly.
c) equivalent effective interest rates are:
i. Semi-annually: 5.06%
ii. Quarterly: 5.11%
iii. Daily: 5.13%
iv. Continuously: 5.13%
EXPLANATION:
To calculate the time it will take for you to save $3,000 for your vacation, we can use the future value formula for monthly compounding:
\(Future Value = Principal * (1 + rate/n)^(n*time)\)
Where:
- Principal is the amount you save each month ($100)
- Rate is the nominal interest rate (3% or 0.03)
- n is the number of compounding periods per year (12 for monthly compounding)
- Time is the number of years we want to calculate
We need to solve for time. Let's substitute the given values into the formula:
\($3,000 = $100 * (1 + 0.03/12)^(12*time)Dividing both sides of the equation by $100:30 = (1.0025)^(12*time)\)
Taking the natural logarithm (ln) of both sides:
\(ln(30) = ln((1.0025)^(12*time))Using logarithmic properties (ln(a^b) = b * ln(a)):ln(30) = 12*time * ln(1.0025)\)
Solving for time:
\(time = ln(30) / (12 * ln(1.0025))\)
Using a calculator:
time ≈ 24.6
c)To calculate the equivalent effective interest rate for a nominal rate of 5% compounded at different intervals:
i. Semi-annually:
The effective interest rate for semi-annual compounding is calculated using the formula:
Effective Interest Rate = (1 + (nominal rate / number of compounding periods))^number of compounding periods - 1
For semi-annual compounding:
\(Effective Interest Rate = (1 + (0.05 / 2))^2 - 1\)
Calculating:
Effective Interest Rate ≈ 0.050625 or 5.06%
ii. Quarterly:
The effective interest rate for quarterly compounding is calculated similarly:
\(Effective Interest Rate = (1 + (0.05 / 4))^4 - 1\)
Calculating:
Effective Interest Rate ≈ 0.051136 or 5.11%
iii. Daily:
The effective interest rate for daily compounding is calculated using the formula:
Effective Interest Rate = (1 + (nominal rate / number of compounding periods))^number of compounding periods - 1
Since there are approximately 365 days in a year:
\(Effective Interest Rate = (1 + (0.05 / 365))^365 - 1\)
Calculating:
Effective Interest Rate ≈ 0.051267 or 5.13%
iv. Continuously:
The effective interest rate for continuous compounding is calculated using the formula:
\(Effective Interest Rate = e^(nominal rate) - 1\)
For a nominal rate of 5%:
\(Effective Interest Rate = e^(0.05) - 1\)
Calculating:
Effective Interest Rate ≈ 0.05127 or 5.13%
Learn more about interest rate :
https://brainly.com/question/29415701
#SPJ11
4. Let -2x+4 if x ≤ 1 f(x) = = Find the value of lim f(x), lim f(x), and lim f(x), or state that they do not exist.
Answers
lim f(x) = 2, lim f(x) = 4, and lim f(x) = DNE, The function f(x) = -2x + 4 if x ≤ 1 and 2x + 2 if x > 1 is a piecewise function.
Piecewise functions are functions that are defined by different expressions in different intervals. In this case, the function is defined by the expression -2x + 4 for x ≤ 1 and the expression 2x + 2 for x > 1.
The limit of a function is the value that the function approaches as the input approaches a certain value. In this case, we are interested in the limits of the function as x approaches 1 from the left, as x approaches 1 from the right, and as x approaches infinity.
The limit of the function as x approaches 1 from the left is the value that the function approaches as x gets closer and closer to 1 from the left. In this case, the function approaches the value 2. This is because the expression -2x + 4 is defined for all values of x that are less than or equal to 1, and the value of -2x + 4 approaches 2 as x approaches 1 from the left.
The limit of the function as x approaches 1 from the right is the value that the function approaches as x gets closer and closer to 1 from the right. In this case, the function approaches the value 4. This is because the expression 2x + 2 is defined for all values of x that are greater than 1, and the value of 2x + 2 approaches 4 as x approaches 1 from the right.
The limit of the function as x approaches infinity is the value that the function approaches as x gets larger and larger. In this case, the function approaches infinity. This is because the expression 2x + 2 grows larger and larger as x gets larger and larger.
Therefore, the limits of the function are 2, 4, and DNE.
Here is a more detailed explanation of the calculation:
The limit of a function is the value that the function approaches as the input approaches a certain value. To find the limit of a function, we can use the following steps:
Substitute the given value into the function.
If the function is defined at the given value, then the limit is the value of the function at that point.
If the function is not defined at the given value, then we can use the following methods to find the limit:
Direct substitution: If the function is defined for all values that are close to the given value, then we can substitute the given value into the function and see what value we get.
L'Hopital's rule: If the function is undefined at the given value, but the function's derivative is defined at the given value, then we can use L'Hopital's rule to find the limit.
Limits at infinity: If the function approaches a certain value as the input gets larger and larger, then we can say that the limit of the function is that value.
In this case, we are interested in the limits of the function as x approaches 1 from the left, as x approaches 1 from the right, and as x approaches infinity.
To find the limit of the function as x approaches 1 from the left, we can substitute x = 1 into the function. This gives us the value 2. Therefore, the limit of the function as x approaches 1 from the left is 2.
To find the limit of the function as x approaches 1 from the right, we can substitute x = 1 into the function. This gives us the value 4. Therefore, the limit of the function as x approaches 1 from the right is 4.
To find the limit of the function as x approaches infinity, we can see that the function approaches infinity as x gets larger and larger. Therefore, the limit of the function as x approaches infinity is infinity.
To know more about function click here
brainly.com/question/28193995
#SPJ11
B 64° x F 60 NOTE: Angles not necessarily drawn to scale. Stuck? Watch a video or use a hint. Report a problem
help

Answers
Answer:
Step-by-step explanation:
x = 56
Please help asap!!!!!!!!

Answers
The y-coordinate for the solution to the system of equations is -3.
What is a system of equations?
A finite set of equations for which common solutions are sought is referred to in mathematics as a set of simultaneous equations, often known as a system of equations. The intersection of two lines represents the system of equations' solution.
Given system of equations are,
6x + 11y = -3
4x + y = 17
To solve these equations, we must first remove x or y terms.
To do this we must make the removing term's coefficients the same.
In this case, let's remove y.
We are multiplying the second equation by 11. Then,
6x + 11y = -3
44x + 11y = 187
Now we will subtract the second equation from the first.
- 38x = -190
x = 5
Now to find y, substitute x in any one of the equations.
6 * 5 + 11y = -3
11y = -33
y = -3
Hence the y-coordinate for the solution to the system of equations is -3.
To learn more about the system of equations, follow the link.
https://brainly.com/question/25976025
#SPJ1
Factorise this pleasee
x2+ 11x+ 18
Answers
Answer:
\((x +9)(x+2)\)
Step-by-step explanation:
Given the problem,
\(x^2 + 11x + 18\)
Factor the problem. Find factors of (18) such that when added the result is (11).
\((x +9)(x+2)\)
Test by distributing, multiply each term in one parenthesis by every term in the other parenthesis,
\((x+9)(x+2)\\\\x^2 + 2x + 9x + 18\\\\x^2 + 11x + 18\)
Answer:
(x+9)(x+2) is your answer
Step-by-step explanation:
x2+ 11x+ 18
x²+9x+2x+18
x(x+9)+2(x+9)
(x+9)(x+2)
PLEASE EXPLAIN ME THIS!!!
I will give the brainliest!
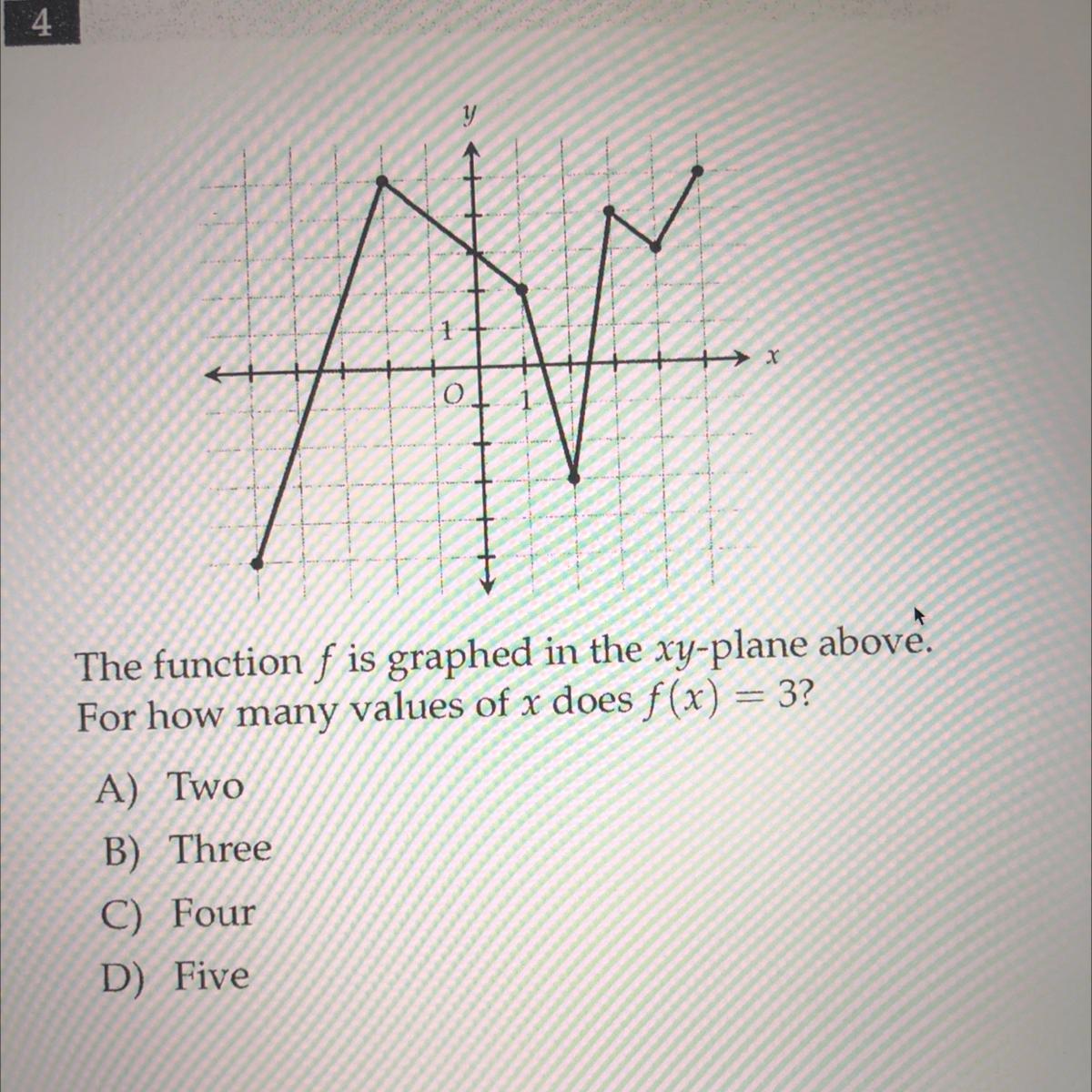
Answers
Remember f(x) = y
If f(x) = x5 â€" 1, g(x) = 5x2, and h(x) = 2x, which expression is equivalent to [g o f o h](9)? 2(5(95 â€" 1)2) 2((5 · 92)5 â€" 1) 5((2 · 9)5 â€" 1)2 (5(2 · 9)2)5 â€" 1
Answers
The equivalent expression for [gofoh](9) is 5(32(9)^5-1).
According to the given question.
We have three functions
f(x) = x^5 - 1
g(x) = 5x^2
h(x) = 2x
Here, we have to find the equivalent expression for [gofoh](9).
so,
gofoh(x)
= g((2x)^5 -1)
= g(32x^5 -1)
= 5(32x^5 -1)
Therefore,
gofoh(9)
= 5(32(9)^5-1)
Hence, the equivalent expression for [gofoh](9) is 5(32(9)^5-1).
Find out more information about equiavlent expression here:
https://brainly.com/question/28170201
#SPJ4
does q have any subgroups isomorphic to z? prove your answer.
Answers
Q does not have any subgroups that are isomorphic to z.
Assume, ⟨a/b⟩∈ ℚ,
Note that under this assumption a/2b ∈ ℚ, which is a rational number, would then be an integral multiple of (a/b), which it clearly is not; i.e. 1/2 × (a/b)
So the assumption that ℚ is generated by (a/b) cannot be true. Since (a/b) is arbitrary, this shows that ℚ is not generated by any element of ℚ, i.e., ℚ is not cyclic.
Since the additive group ℤ =⟨1⟩ is generated by a finite element and is thus cyclic, and ℚ is neither generated by a finite element nor cyclic, the two subgroups are clearly not isomorphic.
#Learn more about isomorphic groups on
https://brainly.com/question/30454143?referrer=searchResults
#SPJ4
Tickets for the school play sell for $4 each. Which graph shows the relationship between the number of tickets s
(x) and the total income from the tickets (y)?
14-
12
Dollars
10
8
6
4
2
14
42
12
SH
4 6
8 10 12 14 X
Tickets

Answers
The graph of (y = 4x), which depicts the relationship between the quantity of tickets sold (x) and the sum of the proceeds from the sales (y), can be drawn by first formulating the linear equation and then using the transformation.
Which is the function's graph?
We have a piecewise function right here:
If x > 6, f(x) = 0.5*x - 2.
If x > 6, f(x) = -x - 1
Given:
Each ticket for the school play is $4.
There have been 'x' tickets sold in total.
The tickets generated 'y' in total revenue.
The graph showing the relationship between the quantity of tickets sold (x) and the sum of the ticket sales (y) can be drawn using the procedures below:
Form the linear equation in two variables as a first step.
y = 4x
The total revenue from the tickets is shown in the equation above.
Draw the graph of (y = x) in step two.
Step 3: In the graph of (y = x), multiply the x-axis by 4 units. The graph that is produced is (y = 4x).
You may find the graph for (y = 4x) below.
If you want to learn more about piecewise functions:
brainly.com/question/3628123
#SPJ1

John is saving to buy a new car that will cost him $24,000. John started his savings at the beginning of the school year and has been able to accumulate $1000 after the first month. John plans to continue his savings at a rate proportional to the amount he still needs to save. Determine John's savings amount as function of time Hint: A variable y is said to be proportional to a variable x if y=cx for some constant c.
Answers
John's savings amount as a function of time is S(t) = $24,000 / 25. Initially, he needs to save $24,000 for a new car. After the first month, he has saved $1,000. The savings amount is directly proportional to the time elapsed. The constant of proportionality is 1/24. Thus, John's savings amount can be determined based on the remaining amount he needs to save.
John's savings amount can be represented as a function of time and is proportional to the amount he still needs to save. Let's denote the amount John needs to save as N(t) at time t, and his savings amount as S(t) at time t. Initially, John needs to save $24,000, so we have N(0) = $24,000.
We know that John has saved $1,000 after the first month, which means S(1) = $1,000. Since his savings amount is proportional to the amount he still needs to save, we can write the proportionality as:
S(t) = k * N(t)
where k is a constant of proportionality.
We need to find the value of k to determine John's savings amount at any given time.
Using the initial values, we can substitute t = 0 and t = 1 into the equation above:
S(0) = k * N(0) => $1,000 = k * $24,000 => k = 1/24
Now we have the value of k, and we can write John's savings amount as a function of time:
S(t) = (1/24) * N(t)
Since John's savings amount is proportional to the amount he still needs to save, we can express the amount he still needs to save at time t as:
N(t) = $24,000 - S(t)
Substituting the expression for N(t) into the equation for S(t), we get:
S(t) = (1/24) * ($24,000 - S(t))
Simplifying the equation, we have:
24S(t) = $24,000 - S(t)
25S(t) = $24,000
S(t) = $24,000 / 25
Therefore, John's savings amount at any given time t is S(t) = $24,000 / 25.
To know more about proportional savings, refer here:
https://brainly.com/question/29251832#
#SPJ11
Nina has $40 in the bank. She writes a check for $63, deposits $80 and writes another check for $140. What is her balance?
Answers
Answer:
-$83
Step-by-step explanation:
Create an equation to model Nina's balance.
\(40-63+80-140=-83\)
Write this is standard form and give degree

Answers
2(-2)^3 - 5(-2)^2 + 4(-2) - 1
-16 - 20 - 8 - 1
-45
Degree is 3 (exponent of leading coefficient)
And cannot write in standard form
NEED HELP ASAP!
Which statement best explains whether the following table represents a linear or nonlinear function?
x −2 −1 0 1 2
y −4 −2 0 2 −2
A) The table represents a nonlinear function because there is not a constant rate of change in the output values.
B) The table represents a nonlinear function because there is not a constant rate of change in the input and output values.
C) The table represents a linear function because there is a constant rate of change in the input and output values.
D) The table represents a linear function because there is not a constant rate of change in the input and output values.
Answers
Answer:
A) The table represents a nonlinear function because there is not a constant rate of change in the output values.
Answer:
D.) The table represents a linear function because there is not a constant rate of change in the input and output values.
Whats the answer to 5/8-2/8?
Answers
Answer:
0.375
Step-by-step explanation: