A polynomial P is given.P(x) = x4 − x2 − 2(a) Find all zeros of P, real and complex. (Enter your answers as a comma-separated list. Enter all answers including repetitions.)x = (b) Factor P completely.P(x) =
Answers
Given:
A polynomial P is:
\(P(x)=x^4-x^2-2\)Required:
(a) Find all zeros of P real and complex.
(b) Factor P completely.
Explanation:
The given polynomial is:
\(P(x)=x^{4}-x^{2}-2\)(a) To find the zeros of the substitute P(x)=0.
\(x^4-x^2-2=0\)Solve it by using the middle-term splitting method.
\(\begin{gathered} x^4-2x^2+x^2-2=0 \\ x^2(x^2-2)+1(x^2-2)=0 \\ (x^2-2)(x^2+1)=0 \end{gathered}\)\(\begin{gathered} x^2-2=0 \\ x^2=2 \\ x=\pm2 \end{gathered}\)\(\begin{gathered} x^2+1=0 \\ x^2=-1 \\ x=\pm\sqrt{-1} \\ x=\pm i \end{gathered}\)Thus the zeros of the given polynomial are
\(\sqrt{2},-\sqrt{2},i,\text{ -i}\)(b)
\(\begin{gathered} P(x)=x^{4}-x^{2}-2 \\ P(x)=x^4-2x^2+x^2-2 \\ P(x)=x^2(x^2-2)+1(x^2-2) \\ P(x)=(x^2-2)(x^2+1) \\ P(x)=(x-\sqrt{2})(x+\sqrt{2})(x^2+1) \end{gathered}\)The factors of the polynomial are
\(\begin{equation*} (x-\sqrt{2})(x+\sqrt{2})(x^2+1) \end{equation*}\)Final Answer:
(a)
\(\sqrt{2},-\sqrt{2},\text{ }\imaginaryI,\text{-}\imaginaryI\)(b)
\(\begin{equation*} (x-\sqrt{2})(x+\sqrt{2})(x^2+1) \end{equation*}\)\(\)Related Questions
Draw a model of 1/2 ÷ 4
Answers
Answer:
1/2 split into 4 parts
Step-by-step explanation:
i cant draw it
Please help?! I'm confused I need help with all of them! and if you can please show your work!! For 50 points!

Answers
Answer:
1 x= 23°
2 x= 148°
3 x= 106°
4 x=17.3°
5 x=25°
6 x=30°
7 x=45°
8 x=48°
9 x=44°
graph of function f defined by f(x) = ab exponent x. what are the possible values of b
Answers
The possible values of b for the given exponential function is found as 5/2.
Explain about the Exponential growth?Exponential growth is the process through which the initial value from the domain grows by an identical percentage across discrete, equal increments.
The exponential function has the following general form: f(x) = abˣ
where an is any nonzero number and b is a positive real number that is not equal to one.
The function expands at a rate proportional from its size if b > 1.The function degenerates at a rate proportionate to its size if 0 < b < 1f(x) = abˣ and f(1) = 2.
Equating both
2 = ab¹ ..eq 1
and .
f(2) = 5
5 = ab² ...eq 1
Divide eq 2 by 1
5/2 = ab² / ab
b = 5/2
Thus, the possible values of b for the given exponential function is found as 5/2.
To know more about the Exponential growth, here
https://brainly.com/question/13223520
#SPJ1
The complete question is-
graph of function f defined by f(x) = ab exponent x. what are the possible values of b: when f(1) = 2 and f(2) = 5.
Write 7% as a decimal
Answers
Answer:
.07
Step-by-step explanation:
8. Factor 36x2 +96x + 64
O(62-8)²
O (6x + 8) (6-8)
(6x+8)²
(18x - 32)²
Answers
The correct answer is (6x+8)^2.
To factor the expression, we can use the perfect square pattern. The perfect square pattern states that a binomial of the form a^2 + 2ab + b^2 can be factored as (a+b)^2.
In this case, we have a=6x and b=8. So, we can factor the expression as follows:
```
36x^2 + 96x + 64 = (6x)^2 + 2(6x)(8) + (8)^2
= (6x + 8)^2
```
log19 1 /2 Rewrite each of the following logarithms using the Change of Base Formula, then round to the nearest ten-thousandth.
Answers
Answer:
-0.2354
Step-by-step explanation:
Change of base formula:
\(log_{b}a = \frac{loga}{logb} \\log_{19}\frac{1}{2} = \frac{log\frac{1}{2} }{log19}\\= -0.2354\)
Hiiii can u please pls pls pls

Answers
Answer:
x | y
0 | 0
6 | 2
12 | 4
Step-by-step explanation:
Multiply each x value in the table by 1/3 to get 0, 2, and 4 for your y values.
Answer:
x y
0 0
6 2
12 4
Step-by-step explanation:
Is means equals
The equation is
y = 1/3 x
Let x = 0
y = 1/3 (0) = 0
Let x = 6
y = 1/3 (6) = 2
Let x = 12
y = 1/3 (12) = 4
Divide x3 – 3x2 + x-2) ÷ 10x414x3_10x2 + 6x = 10 The quotient is ____
The remainder is ____
Answers
Answer:
Im pretty sure X= 5/3
Step-by-step explanation:
Step 1: Simplify both sides of the equation.
x3−3x2+x−2
10
x414)(x3)(0)x2+6x=10
0+6x=10
(6x)+(0)=10(Combine Like Terms)
6x=10
6x=10
Step 2: Divide both sides by 6.
6x
6
=
10
6
x=
5/3
What are the coordinates of the point on
the directed line segment from (1, 2) to
(8,9) that partitions the segment into a
ratio of 6 to 1?
Answers
Answer:
Step-by-step explanation:
=√((x2 – x1)² + (y2 – y1)²)
=√((8 – 1)² + (9 – 2)²)
=√((7)² + (7)²)
=√(49 + 49)
=√(2 • 49)
=7√2
Divide the line segment into 7 parts equally:
=(7√2)/7
=1√2
Multiply to 6 and 1 to get 6:1 ratio:
= 6(1√2)
= 6√2
Final Answer: 6√2 and √2.
Write what the variable n represents in each expression.
L. Lisa can run the 100-yard dash 5 seconds faster than Jerry. Lisa's time is n-5
seconds.
M. Pedro is 3 times younger than his father. Pedro is n + 3 years old.
N. Lucia has $10.00 less than her sister. Lucia has n-10 dollars.
O. Jack is 2 times taller than his younger brother. Jack is 2 x n inches tall.
Answers
The variable n represents time in seconds
The variable n represents age
The variable n represents amount of money in dollars.
The variable n represents height in inches.
In each expression:
L. The variable n represents Jerry's time in seconds for the 100-yard dash. Lisa's time is n-5 seconds, indicating that Lisa runs 5 seconds faster than Jerry.
M. The variable n represents Pedro's father's age in years. Pedro's age is n + 3 years old, meaning Pedro is 3 years younger than his father.
N. The variable n represents Lucia's sister's amount of money in dollars. Lucia has n-10 dollars, indicating that Lucia has $10.00 less than her sister.
O. The variable n represents Jack's younger brother's height in inches. Jack is 2 times taller than his younger brother, so Jack's height is 2 times n inches.
Learn more about expression here:
https://brainly.com/question/28170201
#SPJ1
Can someone help with this question?

Answers
Answer:
supplementary
Step-by-step explanation:
vertices not it bc it's above. and not complementary bc it equal 90 and it's supplement bc line
Three flavors of juice are offered at a school cafeteria The table shows the number of students who purchased each flavor during three lunch
periods
Orange Grape Cherry
51
30
69
Based on the table, what is the probability that a student who bought juice chosen at random purchased the grape flavor
O A. 0.2
B. 0.25
OC. 0,3
D. 0.33
Answers
Answer: A. 0.2
Step-by-step explanation:
Probability for any event = \(\dfrac{\text{Favorable outcomes for event}}{\text{Total possible outcomes}}\)
Three flavors of juice are offered at a school cafeteria.
The given table:
Orange Grape Cherry
51 30 69
Total juices = 51+30+69 =150
Now, the probability that a student who bought juice chosen at random purchased the grape flavor= \(\dfrac{\text{Number of grape juices}}{\text{Total juices}}\)
\(=\dfrac{30}{150}=0.2\)
Hence, the correct option is A.
Answer:
0.2
Step-by-step explanation:
50 POINTS IF CORRECT

Answers
Step-by-step explanation:
I just answered this.
the first group is consistent independent, because both equations are lines with different slope. so, they have 1 intersection, which is the solution.
the second group is consistent dependent, because both equations describe the same line.
multiply the second equation by -2, or divide the first equation by -2, and you see they are identical. multiplying an equation by a factor on both sides does not change the equation or function.
so, as both lines are identical, every point on the line is an intersection and solution. therefore, there are infinitely many solutions.
the third group is inconsistent.
they represent 2 lines with identical slope but different y-interceptions. so, they are parallel and have no intersection or solution at all.
just think : there is no pair of numbers x,y, for which their sum can have 2 different results.
solve: let f(x)=2x-1 and g(x)=x^2-4. find g(f(x))
Answers
Work Shown:
g(x) = x^2 - 4
g(f(x)) = ( f(x) )^2 - 4
g(f(x)) = ( 2x-1 )^2 - 4
g(f(x)) = (2x-1)(2x-1) - 4
g(f(x)) = 4x^2-2x-2x+1 - 4
g(f(x)) = 4x^2 - 4x - 3
Andre and Mai are discussing how to solve for side AB. Andrethinks he can use the equation tan(12) = 3 to solve for AB.Mai thinks she can use the equation tan(78) = to solve forAB. Do you agree with either of them? Show or explain yourreasoning.

Answers
Tangent ratio is the ratio between the opposite and the adjacent sides to given angle.
It depends on the given angle to stablish which is the adjacent and which is the opposite side.
For example, for the angle that measures 12°, the opposite side is the one that measures x and the adjacent is the one that measures 6, it means:
\(\tan 12=\frac{x}{6}\)For the other angle, the one that measures 78, the opposite side now is the one that measures 6 and the adjacent is the one that measures x, it means:
\(\tan 78=\frac{6}{x}\)It means that both Andre and Mai are correct.
Given g(x)=x² - 2x, find the equation of the secant line passing through (-4,g(-4)) and (1,g(1)). Write your answer in the form y=mx+b.
Answers
Answer:
\(y = -5x -2\)
Step-by-step explanation:
Given:
\(g(x) = x^2 -2x\)
Solving for \(\bold{g(-4)}\):
\(g(-4) = (-4)^2 -2(-4) \\ g(-4) = 16 +8 \\ g(-4) = 24\)
This means that \((-4,g(-4))\) is an equivalent statement of \((-4,24)\).
Solving for \(\bold{g(1)}\):
\(g(1) = (1)^2 -2(1) \\ g(-4) = 1 -2 \\ g(-4) = -1\)
This means that \((1,g(1))\) is an equivalent statement of \((1,-1)\).
Now we have the two points of the line, \((-4,24)\) and \((1,-1)\), we can finally solve for its slope, \(m\). Recall that \(m = \frac{y_2 -y_1}{x_2 -x_1}\\\).
\(m = \frac{-1 -24}{1 -(-4)} \\ m = \frac{-25}{5} \\ m = -5\)
Now that we know our slope, we can then write it as point-slope form and then rewrite it in its slope-intercept form as we are asked. Recall that an equation of a line in its point-slope form is write, \(y -y_1 = m(x -x_1)\), where \(y_1\) and \(x_1\) is \(y\) and \(x\) coordinates of any point of a line respectively.
Writing for the equation of a line in its point-slope form with the point \(\bold{(1,-1)}\):
\(y -(-1) = -5(x -1) \\ y +1 = -5(x -1)\)
Rewriting for the equation of a line in its slope-intercept form:
\(y +1 = -5(x -1) \\ y +1 = -5x -1 \\ y = -5x -2\)
in the notation “s(x)=...,” what does “s(x)” represent
Answers
The statement s(x) means that s is a function of x
How to interpret the function notationFrom the question, we have the following parameters that can be used in our computation:
s(x)
The above is a function notation
Generally, the expression f(x) means that f is a function of x
When f is replaced with s, we have
s is a function of x
Hence, the meaning is that "s is a function of x"
Read more about functions at
https://brainly.com/question/28277110
#SPJ1
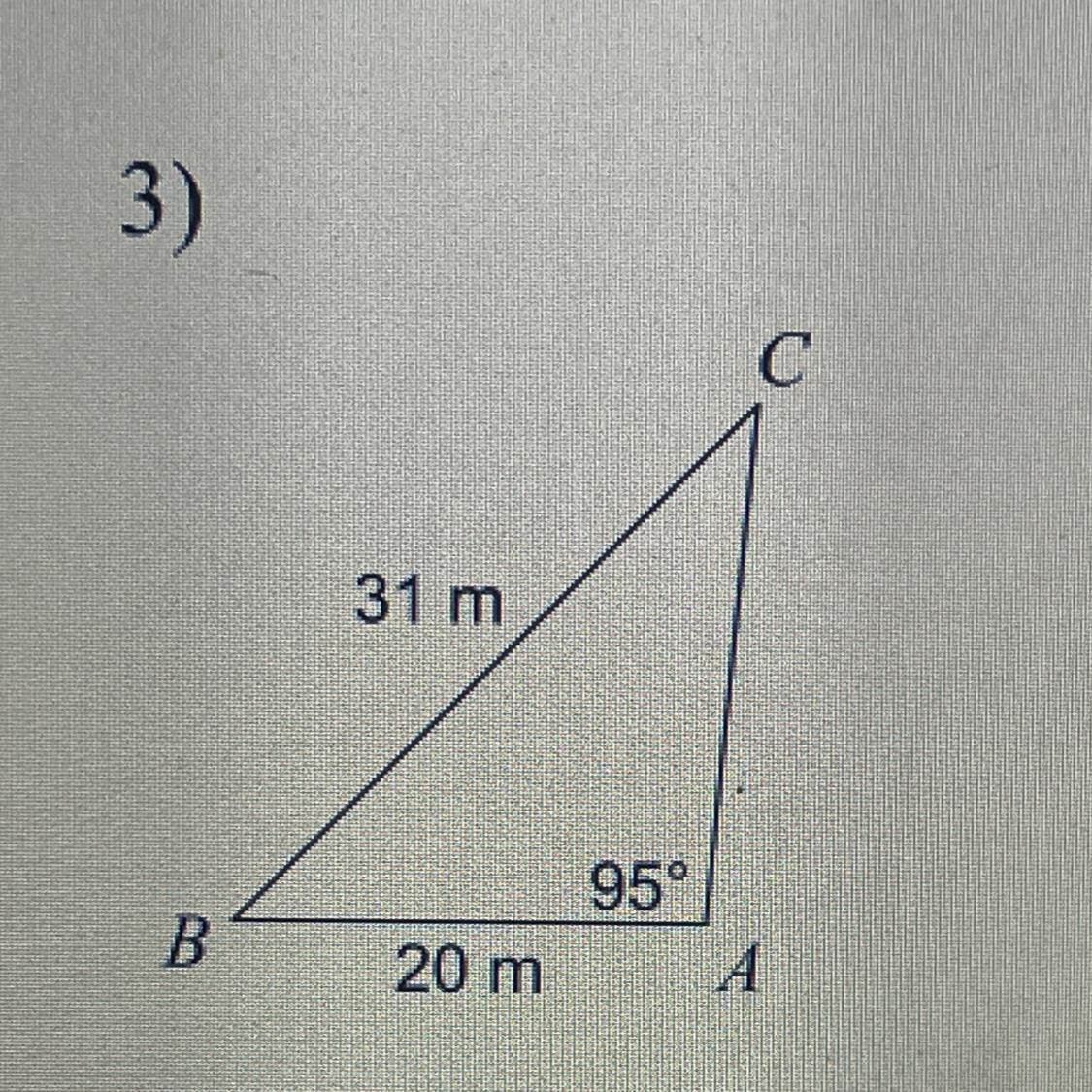
Solve each triangle. Round your answers to the nearest tenth.
Answers
The length of AC = 3.55.
In the given triangle,
AB = 20 m = c
BC = 31 m = b
AC = a = ?
∠A = 95 degree
We know the cosine rule,
CosA = (b² + c² - a²)/2bc
Therefore,
⇒ Cos95 = (31² + 20² - a²)/(2x31x20)
⇒ -0.087 = (1361 - a²)/1240
⇒ -107.88 = (1361 - a²)
⇒ a² = 12.62
⇒ a = 3.55
Hence,
AC = 3.55.
Learn more about the triangles visit;
brainly.com/question/1058720
#SPJ1
Calculate the volume of a triangular pyramid 12cm tall and with a base 12cm long and 10cm wide
Answers
Remember that the volume of a triangular pyramid can be calculated using the formula:
\(V=\frac{A_{base}\cdot height}{3}\)So first, let's calculate the area of the base:
\(A_{base}=\frac{10\cdot12}{2}=60\)Using this in the formula,
\(V=\frac{60\cdot12}{3}=240\)Thereby, the volume of the pyramid is 240 cubic centimiters
please answer both questions thanks

Answers
Answer:
8. cos(58) = 20/x
x · cos(58) = 20
x = 20/cos(58)
= 37.742
≈ 37.7
9. tan(69) = 324/x
x · tan(69) = 324
x = 324/tan(69)
= 124.372
≈ 124.4

Help me please! I need an answer!

Answers
Answer: \(\bold{\dfrac{b_1}{b_2}=\dfrac{3}{2}}\)
Step-by-step explanation:
Inversely proportional means a x b = k --> b = k/a
Given that a₁ = 2 --> b₁ = k/2
Given that a₂ = 3 --> b₂ = k/3
\(\dfrac{b_1}{b_2}=\dfrac{\frac{k}{2}}{\frac{k}{3}}=\large\boxed{\dfrac{3}{2}}\)
18. If Allan swims at an average speed of 2
metres per second, how long will it take
him to complete a 200 metre race?
Answers
Answer:
100 seconds
Step-by-step explanation:
200/2 = 100s
I just need help with the range domain is [-2,3)

Answers
Answer:
We don't need to worry about the displaystyle- {3} −3 anyway, because we dcided in the first step that displaystyle {x}ge- {2} x ≥ −2. So the domain for this case is displaystyle {x}ge- {2}, {x}ne {3} x≥ −2,x≠ 3, which we can write as displaystyle {left [- {2}, {3}right)}cup {left ({3},inftyright)} [−2,3)∪(3,∞).
Step-by-step explanation:
use lagrange multipliers to find the maximum or minimum values of the function subject to the given constraint. (if an answer does not exist, enter dne.) f(x, y, z)
Answers
To determine the maximum or minimum value of a given function, Lagrange multipliers are used.
What is langrange multipliers?
Let's set up everything now. We want to optimize (i.e., find the minimum and maximum value of) a function, f, under the condition that g (x, y, and z) = k. (x, y, and z). Once more, the equation that describes the boundary of a region may or may not be the constraint. Although the process is actually quite simple, there are times when the workload seems quite overwhelming.
Solve the following system of equations.
∇f(x,y,z) = λ
∇g(x,y,z)
g(x,y,z)= k
If there are minimum and maximum values, enter them into f(x,y,z) along with all of the solutions (x,y,z) from the first step.
∇ g ≠ → 0 at the point.
The constant, λ, is called the Lagrange Multiplier.
To know more about lagrange multiplier here:
https://brainly.com/question/4609414
#SPJ4
Please help 2 questions with details and work out please

Answers
From properties of parallel lines the value of the indicated angle is 84° and the value of x is 4°.
Parallel lines are two lines that are equidistant from one another.
Parallel lines in geometry are coplanar, straight lines that don't cross at any point. In the same three-dimensional space, parallel planes are any planes that never cross.A line that intersects both the parallel lines is called a transversal.A set of angles on the inner side of each of the two lines but on the opposing sides of the transversal are known as alternate interior angles.Alternate external angles are those outside the two lines that the transversal is intersecting.For the question 7 the two lines are parallel and the indicated angle is an alternate interior angle to the given angle. Hence the indicated angle is also 84°.
For question 8, the two angles are alternate exterior angles.
Hence they are equal. Therefore we can write a linear equation in x to solve for x.
21x+6=90
or, 21x=84
or, x=4°
To learn more about parallel lines visit:
https://brainly.com/question/19714372
#SPJ9
which number is an integers
-3/4
1/5
2
42/3
Answers
Why do we choose 5% as a risk of making error and not 1%
Answers
In statistics, the risk of making an error is referred to as a significance level. A significance level represents the probability of making a Type I error, which occurs when a null hypothesis is rejected even though it is true.
The most common significance level used in statistical analyses is 0.05 or 5%. This means that there is a 5% chance of rejecting a true null hypothesis.
In general, the choice of significance level depends on the specific application and context of the statistical analysis.
The 5% significance level is commonly used in scientific research, particularly in the fields of medicine and psychology.
The choice of this level is based on a balance between the risk of making a Type I error and the risk of making a Type II error, which occurs when a null hypothesis is not rejected even though it is false.
A Type II error is often more serious than a Type I error since it may lead to incorrect conclusions about the relationship between variables or the effectiveness of a treatment or intervention.
A 5% significance level provides a reasonable balance between these two types of errors. However, in some situations, a higher or lower significance level may be more appropriate.
For example, in a clinical trial where the consequences of a Type II error are severe, a lower significance level may be used to reduce the risk of this type of error.
To learn more about : probability
https://brainly.com/question/251701
#SPJ8
Kure wants to share three pies among 11 people. Her calculator shows 0.272727272727. Determine whether the rounding should occur and give the rounded answer
Answers
Answer:
She should convert it to a fraction and give each person a quarter of a pie.
Step-by-step explanation:
Y varies inversely with x. If Y=17 and k(The constant of variation) =76, what is x? Round to the nearest tenth if necessary.
Answers
Answer:
x ≈ 4.5
Step-by-step explanation:
Given y varies inversely with x then the equation relating them is
y = \(\frac{k}{x}\) ← k is the constant of variation
Here k = 76 and y = 17 , thus
17 = \(\frac{76}{x}\) ( multiply both sides by x )
17x = 76 ( divide both sides by 17 )
x ≈ 4.5 ( to the nearest tenth )
find the value of p in the following equation: 6 * 2/4 = p * 1/4
Answers
Answer: \(p=12\)
Step-by-step explanation:
\(6*\frac{2}{4}=p*\frac{1}{4}\)
Solve the multiplication on the left side.
6 and 4 can be simplified.
6/2=3
4/2=2
Leaving it like;
\(3*\frac{2}{2}=p*\frac{1}{4}\)
2 and 2 is 1 and 3 times 1 is 3.
\(3=p*\frac{1}{4}\)
Multiply by 4 to eliminate the fraction and isolate p.
\(4*3=p*\frac{1}{4}*4\\12=p\)